Johnson's algorithm for Allpairs shortest paths (original) (raw)
Last Updated : 03 Apr, 2025
The problem is to find the shortest paths between every pair of vertices in a given weighted directed Graph and weights may be negative. We have discussed Floyd Warshall Algorithm for this problem. The time complexity of the Floyd Warshall Algorithm is Θ(V3).
_Using Johnson's algorithm, we can find all pair shortest paths in O(V 2 log V + VE) time. Johnson’s algorithm uses both Dijkstra and Bellman-Ford as subroutines. If we apply Dijkstra's Single Source shortest path algorithm for every vertex, considering every vertex as the source, we can find all pair shortest paths in O(V*(V + E) * Log V) time.
So using Dijkstra's single-source shortest path seems to be a better option than Floyd Warshall's Algorithm , but the problem with Dijkstra's algorithm is, that it doesn't work for negative weight edge. _The idea of Johnson's algorithm is to re-weight all edges and make them all positive, then apply Dijkstra's algorithm for every vertex.
**How to transform a given graph into a graph with all non-negative weight edges?
One may think of a simple approach of finding the minimum weight edge and adding this weight to all edges. Unfortunately, this doesn't work as there may be a different number of edges in different paths (See this for an example). If there are multiple paths from a vertex u to v, then all paths must be increased by the same amount, so that the shortest path remains the shortest in the transformed graph. The idea of Johnson's algorithm is to assign a weight to every vertex. Let the weight assigned to vertex u be h[u].
We reweight edges using vertex weights. For example, for an edge (u, v) of weight w(u, v), the new weight becomes w(u, v) + h[u] - h[v]. The great thing about this reweighting is, that all set of paths between any two vertices is increased by the same amount and all negative weights become non-negative. Consider any path between two vertices s and t, the weight of every path is increased by h[s] - h[t], and all h[] values of vertices on the path from s to t cancel each other.
How do we calculate h[] values?
Bellman-Ford algorithm is used for this purpose. Following is the complete algorithm. A new vertex is added to the graph and connected to all existing vertices. The shortest distance values from the new vertex to all existing vertices are h[] values.
**Algorithm:
- Let the given graph be G. Add a new vertex s to the graph, add edges from the new vertex to all vertices of G. Let the modified graph be G'.
- Run the Bellman-Ford algorithm on G' with s as the source. Let the distances calculated by Bellman-Ford be h[0], h[1], .. h[V-1]. If we find a negative weight cycle, then return. Note that the negative weight cycle cannot be created by new vertex s as there is no edge to s. All edges are from s.
- Reweight the edges of the original graph. For each edge (u, v), assign the new weight as "original weight + h[u] - h[v]".
- Remove the added vertex s and run Dijkstra's algorithm for every vertex.
**How does the transformation ensure nonnegative weight edges?
The following property is always true about h[] values as they are the shortest distances.
h[v] <= h[u] + w(u, v)
The property simply means that the shortest distance from s to v must be smaller than or equal to the shortest distance from s to u plus the weight of the edge (u, v). The new weights are w(u, v) + h[u] - h[v]. The value of the new weights must be greater than or equal to zero because of the inequality "h[v] <= h[u] + w(u, v)".
**Example: Let us consider the following graph.

We add a source s and add edges from s to all vertices of the original graph. In the following diagram s is 4.

We calculate the shortest distances from 4 to all other vertices using Bellman-Ford algorithm. The shortest distances from 4 to 0, 1, 2 and 3 are 0, -5, -1 and 0 respectively, i.e., h[] = {0, -5, -1, 0}. Once we get these distances, we remove the source vertex 4 and reweight the edges using following formula. w(u, v) = w(u, v) + h[u] - h[v].
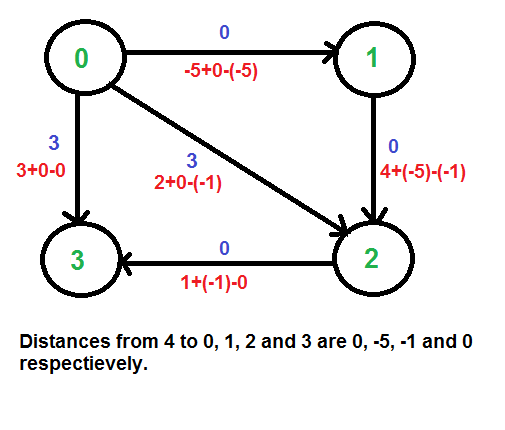
Since all weights are positive now, we can run Dijkstra's shortest path algorithm for every vertex as the source.
C++ `
#include #include #include #include
#define INF std::numeric_limits::max()
using namespace std;
// Function to find the vertex with the minimum distance // that has not yet been included in the shortest path tree int Min_Distance(const vector& dist, const vector& visited) { int min = INF, min_index; for (int v = 0; v < dist.size(); ++v) { if (!visited[v] && dist[v] <= min) { min = dist[v]; min_index = v; } } return min_index; }
// Function to perform Dijkstra's algorithm on the modified graph void Dijkstra_Algorithm(const vector<vector>& graph, const vector<vector>& altered_graph, int source) { int V = graph.size(); // Number of vertices vector dist(V, INF); // Distance from source to each vertex vector visited(V, false); // Track visited vertices
dist[source] = 0; // Distance to source itself is 0
// Compute shortest path for all vertices
for (int count = 0; count < V - 1; ++count) {
// Select the vertex with the minimum distance that hasn't been visited
int u = Min_Distance(dist, visited);
visited[u] = true; // Mark this vertex as visited
// Update the distance value of the adjacent vertices of the selected vertex
for (int v = 0; v < V; ++v) {
if (!visited[v] && graph[u][v] != 0 && dist[u] != INF && dist[u] + altered_graph[u][v] < dist[v]) {
dist[v] = dist[u] + altered_graph[u][v];
}
}
}
// Print the shortest distances from the source
cout << "Shortest Distance from vertex " << source << ":\n";
for (int i = 0; i < V; ++i) {
cout << "Vertex " << i << ": " << (dist[i] == INF ? "INF" : to_string(dist[i])) << endl;
}}
// Function to perform Bellman-Ford algorithm to find shortest distances // from a source vertex to all other vertices vector BellmanFord_Algorithm(const vector<vector>& edges, int V) { vector dist(V + 1, INF); // Distance from source to each vertex dist[V] = 0; // Distance to the new source vertex (added vertex) is 0
// Add a new source vertex to the graph and connect it to all original vertices with 0 weight edges
vector<vector<int>> edges_with_extra(edges);
for (int i = 0; i < V; ++i) {
edges_with_extra.push_back({V, i, 0});
}
// Relax all edges |V| - 1 times
for (int i = 0; i < V; ++i) {
for (const auto& edge : edges_with_extra) {
if (dist[edge[0]] != INF && dist[edge[0]] + edge[2] < dist[edge[1]]) {
dist[edge[1]] = dist[edge[0]] + edge[2];
}
}
}
return vector<int>(dist.begin(), dist.begin() + V); // Return distances excluding the new source vertex}
// Function to implement Johnson's Algorithm void JohnsonAlgorithm(const vector<vector>& graph) { int V = graph.size(); // Number of vertices vector<vector> edges;
// Collect all edges from the graph
for (int i = 0; i < V; ++i) {
for (int j = 0; j < V; ++j) {
if (graph[i][j] != 0) {
edges.push_back({i, j, graph[i][j]});
}
}
}
// Get the modified weights from Bellman-Ford algorithm
vector<int> altered_weights = BellmanFord_Algorithm(edges, V);
vector<vector<int>> altered_graph(V, vector<int>(V, 0));
// Modify the weights of the edges to remove negative weights
for (int i = 0; i < V; ++i) {
for (int j = 0; j < V; ++j) {
if (graph[i][j] != 0) {
altered_graph[i][j] = graph[i][j] + altered_weights[i] - altered_weights[j];
}
}
}
// Print the modified graph with re-weighted edges
cout << "Modified Graph:\n";
for (const auto& row : altered_graph) {
for (int weight : row) {
cout << weight << ' ';
}
cout << endl;
}
// Run Dijkstra's algorithm for every vertex as the source
for (int source = 0; source < V; ++source) {
cout << "\nShortest Distance with vertex " << source << " as the source:\n";
Dijkstra_Algorithm(graph, altered_graph, source);
}}
// Main function to test the Johnson's Algorithm implementation int main() { // Define a graph with possible negative weights vector<vector> graph = { {0, -5, 2, 3}, {0, 0, 4, 0}, {0, 0, 0, 1}, {0, 0, 0, 0} };
// Execute Johnson's Algorithm
JohnsonAlgorithm(graph);
return 0;}
Java
import java.util.Arrays;
public class GFG {
// Define infinity as a large integer value
private static final int INF = Integer.MAX_VALUE;
// Function to find the vertex with the minimum distance
// from the source that has not yet been included in the shortest path tree
private static int minDistance(int[] dist, boolean[] sptSet) {
int min = INF, minIndex = 0;
for (int v = 0; v < dist.length; v++) {
// Update minIndex if a smaller distance is found
if (!sptSet[v] && dist[v] <= min) {
min = dist[v];
minIndex = v;
}
}
return minIndex;
}
// Function to perform Dijkstra's algorithm on the modified graph
private static void dijkstraAlgorithm(int[][] graph, int[][] alteredGraph, int source) {
int V = graph.length; // Number of vertices
int[] dist = new int[V]; // Distance array to store shortest distance from source
boolean[] sptSet = new boolean[V]; // Boolean array to track visited vertices
// Initialize distances with infinity and source distance as 0
Arrays.fill(dist, INF);
dist[source] = 0;
// Compute shortest path for all vertices
for (int count = 0; count < V - 1; count++) {
// Pick the vertex with the minimum distance that hasn't been visited
int u = minDistance(dist, sptSet);
sptSet[u] = true; // Mark this vertex as visited
// Update distance values for adjacent vertices
for (int v = 0; v < V; v++) {
// Check for updates to the distance value
if (!sptSet[v] && graph[u][v] != 0 && dist[u] != INF && dist[u] + alteredGraph[u][v] < dist[v]) {
dist[v] = dist[u] + alteredGraph[u][v];
}
}
}
// Print the shortest distances from the source vertex
System.out.println("Shortest Distance from vertex " + source + ":");
for (int i = 0; i < V; i++) {
System.out.println("Vertex " + i + ": " + (dist[i] == INF ? "INF" : dist[i]));
}
}
// Function to perform Bellman-Ford algorithm to calculate shortest distances
// from a source vertex to all other vertices
private static int[] bellmanFordAlgorithm(int[][] edges, int V) {
int[] dist = new int[V + 1]; // Distance array with an extra vertex
Arrays.fill(dist, INF);
dist[V] = 0; // Distance to the new source vertex (added vertex) is 0
// Add edges from the new source vertex to all original vertices
int[][] edgesWithExtra = Arrays.copyOf(edges, edges.length + V);
for (int i = 0; i < V; i++) {
edgesWithExtra[edges.length + i] = new int[]{V, i, 0};
}
// Relax all edges |V| - 1 times
for (int i = 0; i < V; i++) {
for (int[] edge : edgesWithExtra) {
if (dist[edge[0]] != INF && dist[edge[0]] + edge[2] < dist[edge[1]]) {
dist[edge[1]] = dist[edge[0]] + edge[2];
}
}
}
return Arrays.copyOf(dist, V); // Return distances excluding the new source vertex
}
// Function to implement Johnson's Algorithm
private static void johnsonAlgorithm(int[][] graph) {
int V = graph.length; // Number of vertices
int[][] edges = new int[V * (V - 1) / 2][3]; // Array to store edges
int index = 0;
// Collect all edges from the graph
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (graph[i][j] != 0) {
edges[index++] = new int[]{i, j, graph[i][j]};
}
}
}
// Get the modified weights to remove negative weights using Bellman-Ford
int[] alteredWeights = bellmanFordAlgorithm(edges, V);
int[][] alteredGraph = new int[V][V];
// Modify the weights of the edges to ensure all weights are non-negative
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (graph[i][j] != 0) {
alteredGraph[i][j] = graph[i][j] + alteredWeights[i] - alteredWeights[j];
}
}
}
// Print the modified graph with re-weighted edges
System.out.println("Modified Graph:");
for (int[] row : alteredGraph) {
for (int weight : row) {
System.out.print(weight + " ");
}
System.out.println();
}
// Run Dijkstra's algorithm for each vertex as the source
for (int source = 0; source < V; source++) {
System.out.println("\nShortest Distance with vertex " + source + " as the source:");
dijkstraAlgorithm(graph, alteredGraph, source);
}
}
// Main function to test Johnson's Algorithm
public static void main(String[] args) {
// Define a graph with possible negative weights
int[][] graph = {
{0, -5, 2, 3},
{0, 0, 4, 0},
{0, 0, 0, 1},
{0, 0, 0, 0}
};
// Execute Johnson's Algorithm
johnsonAlgorithm(graph);
}}
Python
Implementation of Johnson's algorithm in Python3
Import function to initialize the dictionary
from collections import defaultdict INT_MAX = float('Inf')
Function that returns the vertex
with minimum distance
from the source
def Min_Distance(dist, visit):
(minimum, Minimum_Vertex) = (INT_MAX, 0)
for vertex in range(len(dist)):
if minimum > dist[vertex] and visit[vertex] == False:
(minimum, minVertex) = (dist[vertex], vertex)
return Minimum_VertexDijkstra Algorithm for Modified
Graph (After removing the negative weights)
def Dijkstra_Algorithm(graph, Altered_Graph, source):
# Number of vertices in the graph
tot_vertices = len(graph)
# Dictionary to check if given vertex is
# already included in the shortest path tree
sptSet = defaultdict(lambda : False)
# Shortest distance of all vertices from the source
dist = [INT_MAX] * tot_vertices
dist[source] = 0
for count in range(tot_vertices):
# The current vertex which is at min Distance
# from the source and not yet included in the
# shortest path tree
curVertex = Min_Distance(dist, sptSet)
sptSet[curVertex] = True
for vertex in range(tot_vertices):
if ((sptSet[vertex] == False) and
(dist[vertex] > (dist[curVertex] +
Altered_Graph[curVertex][vertex])) and
(graph[curVertex][vertex] != 0)):
dist[vertex] = (dist[curVertex] +Altered_Graph[curVertex][vertex])
# Print the Shortest distance from the source
for vertex in range(tot_vertices):
print ('Vertex ' + str(vertex) + ': ' + str(dist[vertex]))Function to calculate shortest distances from source
to all other vertices using Bellman-Ford algorithm
def BellmanFord_Algorithm(edges, graph, tot_vertices):
# Add a source s and calculate its min
# distance from every other node
dist = [INT_MAX] * (tot_vertices + 1)
dist[tot_vertices] = 0
for i in range(tot_vertices):
edges.append([tot_vertices, i, 0])
for i in range(tot_vertices):
for (source, destn, weight) in edges:
if((dist[source] != INT_MAX) and
(dist[source] + weight < dist[destn])):
dist[destn] = dist[source] + weight
# Don't send the value for the source added
return dist[0:tot_vertices]Function to implement Johnson Algorithm
def JohnsonAlgorithm(graph):
edges = []
# Create a list of edges for Bellman-Ford Algorithm
for i in range(len(graph)):
for j in range(len(graph[i])):
if graph[i][j] != 0:
edges.append([i, j, graph[i][j]])
# Weights used to modify the original weights
Alter_weigts = BellmanFord_Algorithm(edges, graph, len(graph))
Altered_Graph = [[0 for p in range(len(graph))] for q in
range(len(graph))]
# Modify the weights to get rid of negative weights
for i in range(len(graph)):
for j in range(len(graph[i])):
if graph[i][j] != 0:
Altered_Graph[i][j] = (graph[i][j] +
Alter_weigts[i] - Alter_weigts[j]);
print ('Modified Graph: ' + str(Altered_Graph))
# Run Dijkstra for every vertex as source one by one
for source in range(len(graph)):
print ('\nShortest Distance with vertex ' +
str(source) + ' as the source:\n')
Dijkstra_Algorithm(graph, Altered_Graph, source)Driver Code
graph = [[0, -5, 2, 3], [0, 0, 4, 0], [0, 0, 0, 1], [0, 0, 0, 0]]
JohnsonAlgorithm(graph)
` JavaScript ``
const INF = Number.MAX_VALUE;
// Function to find the vertex with minimum distance from the source function minDistance(dist, visited) { let min = INF; let minIndex = -1;
for (let v = 0; v < dist.length; v++) {
if (!visited[v] && dist[v] < min) {
min = dist[v];
minIndex = v;
}
}
return minIndex;}
// Function to perform Dijkstra's algorithm on the modified graph function dijkstraAlgorithm(graph, alteredGraph, source) { const V = graph.length; const dist = Array(V).fill(INF); const visited = Array(V).fill(false);
dist[source] = 0;
for (let count = 0; count < V - 1; count++) {
const u = minDistance(dist, visited);
visited[u] = true;
for (let v = 0; v < V; v++) {
if (!visited[v] && graph[u][v] !== 0 && dist[u] !== INF && dist[u] + alteredGraph[u][v] < dist[v]) {
dist[v] = dist[u] + alteredGraph[u][v];
}
}
}
console.log(`Shortest Distance from vertex ${source}:`);
for (let i = 0; i < V; i++) {
console.log(`Vertex <span class="katex"><span class="katex-mathml"><math xmlns="http://www.w3.org/1998/Math/MathML"><semantics><mrow><mi>i</mi><mo>:</mo></mrow><annotation encoding="application/x-tex">{i}: </annotation></semantics></math></span><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6595em;"></span><span class="mord"><span class="mord mathnormal">i</span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">:</span></span></span></span>{dist[i] === INF ? "INF" : dist[i]}`);
}}
// Function to perform Bellman-Ford algorithm to calculate shortest distances function bellmanFordAlgorithm(edges, V) { const dist = Array(V + 1).fill(INF); dist[V] = 0;
const edgesWithExtra = edges.slice();
for (let i = 0; i < V; i++) {
edgesWithExtra.push([V, i, 0]);
}
for (let i = 0; i < V; i++) {
for (const [src, dest, weight] of edgesWithExtra) {
if (dist[src] !== INF && dist[src] + weight < dist[dest]) {
dist[dest] = dist[src] + weight;
}
}
}
return dist.slice(0, V);}
// Function to implement Johnson's Algorithm function johnsonAlgorithm(graph) { const V = graph.length; const edges = [];
for (let i = 0; i < V; i++) {
for (let j = 0; j < V; j++) {
if (graph[i][j] !== 0) {
edges.push([i, j, graph[i][j]]);
}
}
}
const alteredWeights = bellmanFordAlgorithm(edges, V);
const alteredGraph = Array.from({ length: V }, () => Array(V).fill(0));
for (let i = 0; i < V; i++) {
for (let j = 0; j < V; j++) {
if (graph[i][j] !== 0) {
alteredGraph[i][j] = graph[i][j] + alteredWeights[i] - alteredWeights[j];
}
}
}
console.log("Modified Graph:");
alteredGraph.forEach(row => {
console.log(row.join(' '));
});
for (let source = 0; source < V; source++) {
console.log(`\nShortest Distance with vertex ${source} as the source:`);
dijkstraAlgorithm(graph, alteredGraph, source);
}}
// Driver Code const graph = [ [0, -5, 2, 3], [0, 0, 4, 0], [0, 0, 0, 1], [0, 0, 0, 0] ];
johnsonAlgorithm(graph);
``
Output
Following matrix shows the shortest distances between every pair of vertices 0 5 8 9 INF 0 3 4 INF INF 0 1 INF INF INF 0
**Time Complexity: The main steps in the algorithm are Bellman-Ford Algorithm called once and Dijkstra called V times. Time complexity of Bellman Ford is O(VE) and time complexity of Dijkstra is O((V + E)Log V). So overall time complexity is O(V2log V + VE).
The time complexity of Johnson's algorithm becomes the same as Floyd Warshall's Algorithm when the graph is complete (For a complete graph E = O(V2). But for sparse graphs, the algorithm performs much better than Floyd Warshall's Algorithm.
**Auxiliary Space: O(V2)