Level with maximum number of nodes (original) (raw)

Last Updated : 25 Apr, 2025

Try it on GfG Practice

Given a binary tree, the task is to find the level in a binary tree that has the maximum number of nodes.

**Note: The root is at level 0.

**Examples:

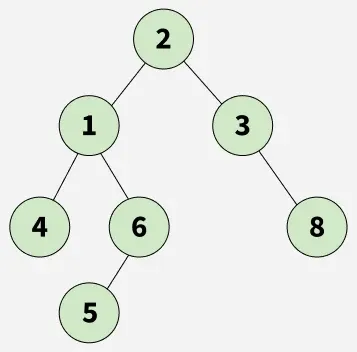
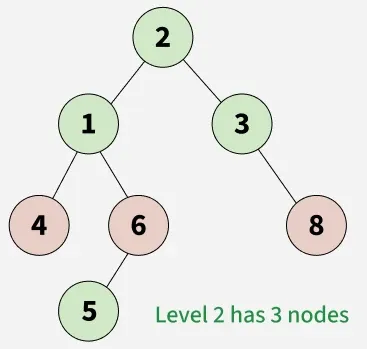
**Input: Binary Tree

**Output : 2
**Explanation:

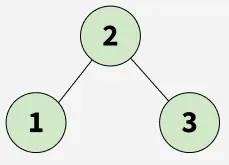
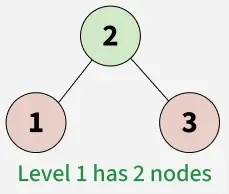
**Input: Binary tree

****Output:**1
**Explanation

Using Breadth First Search - O(n) time and O(n) space

The idea is to traverse the binary tree level by level, keeping track of the number of nodes at each level. As we process each level, we compare its node count with the maximum count found so far, updating our result level if the current level has more nodes. The queue-based BFS naturally groups nodes by their level, making it straightforward to count nodes per level.

Step by step approach:

1. Start with root node in the queue and initialize tracking variables for level, max nodes, and result level.
2. For each level, record its size (number of nodes) from the queue before processing.
3. If current level's size exceeds previous maximum, update the maximum count and result level.
4. Process all nodes at current level, adding their children to queue for next level processing.
5. Return the level that had the maximum number of nodes after all levels are processed. C++ `

// C++ code to find Level with maximum number of nodes using BFS #include #include using namespace std;

class Node { public: int data; Node *left, *right; Node(int x) { data = x; left = nullptr; right = nullptr; } };

int maxNodeLevel(Node *root) { if (root == nullptr) return -1;

queue<Node*> q;
q.push(root);

int level = 0;
int maxNodes = 0;
int maxLevel = 0;

while (!q.empty()) {
    
    // Number of nodes at current level
    int size = q.size();  
    
    if (size > maxNodes) {
        maxNodes = size;
        maxLevel = level;
    }
    
    // Process all nodes at current level
    for (int i = 0; i < size; i++) {
        Node* current = q.front();
        q.pop();
        
        if (current->left)
            q.push(current->left);
        if (current->right)
            q.push(current->right);
    }
    
    level++;
}

return maxLevel;

}

int main() {

//          2
//        /   \
//       1     3
//      / \     \
//     4   6     8
//    /
//   5
Node* root = new Node(2);
root->left = new Node(1);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(6);
root->right->right = new Node(8);
root->left->left->left = new Node(5);

cout <<  maxNodeLevel(root) << endl;

return 0;

}

Java

// Java code to find Level with maximum number of nodes using BFS import java.util.Queue; import java.util.LinkedList;

class Node { int data; Node left, right; Node(int x) { data = x; left = null; right = null; } }

class GfG {

// A function to find level with maximum number of nodes
static int maxNodeLevel(Node root) {
    if (root == null)
        return -1;

    Queue<Node> q = new LinkedList<>();
    q.add(root);

    int level = 0;
    int maxNodes = 0;
    int maxLevel = 0;

    while (!q.isEmpty()) {

        // Number of nodes at current level
        int size = q.size();  

        if (size > maxNodes) {
            maxNodes = size;
            maxLevel = level;
        }

        // Process all nodes at current level
        for (int i = 0; i < size; i++) {
            Node current = q.poll();

            if (current.left != null)
                q.add(current.left);
            if (current.right != null)
                q.add(current.right);
        }

        level++;
    }

    return maxLevel;
}

public static void main(String[] args) {

    //          2
    //        /   \
    //       1     3
    //      / \     \
    //     4   6     8
    //    /
    //   5
    Node root = new Node(2);
    root.left = new Node(1);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(6);
    root.right.right = new Node(8);
    root.left.left.left = new Node(5);

    System.out.println(maxNodeLevel(root));
}

}

Python

Python code to find Level with maximum number of nodes using BFS

from collections import deque

class Node: def init(self, x): self.data = x self.left = None self.right = None

A function to find level with maximum number of nodes

def maxNodeLevel(root): if root is None: return -1

q = deque()
q.append(root)

level = 0
maxNodes = 0
maxLevel = 0

while q:

    # Number of nodes at current level
    size = len(q)

    if size > maxNodes:
        maxNodes = size
        maxLevel = level

    # Process all nodes at current level
    for _ in range(size):
        current = q.popleft()

        if current.left:
            q.append(current.left)
        if current.right:
            q.append(current.right)

    level += 1

return maxLevel

if name == "main":

#          2
#        /   \
#       1     3
#      / \     \
#     4   6     8
#    /
#   5
root = Node(2)
root.left = Node(1)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(6)
root.right.right = Node(8)
root.left.left.left = Node(5)

print(maxNodeLevel(root))

C#

// C# code to find Level with maximum number of nodes using BFS using System; using System.Collections.Generic;

class Node { public int data; public Node left, right; public Node(int x) { data = x; left = null; right = null; } }

class GfG {

// A function to find level with maximum number of nodes
static int maxNodeLevel(Node root) {
    if (root == null)
        return -1;

    Queue<Node> q = new Queue<Node>();
    q.Enqueue(root);

    int level = 0;
    int maxNodes = 0;
    int maxLevel = 0;

    while (q.Count > 0) {

        // Number of nodes at current level
        int size = q.Count;

        if (size > maxNodes) {
            maxNodes = size;
            maxLevel = level;
        }

        // Process all nodes at current level
        for (int i = 0; i < size; i++) {
            Node current = q.Dequeue();

            if (current.left != null)
                q.Enqueue(current.left);
            if (current.right != null)
                q.Enqueue(current.right);
        }

        level++;
    }

    return maxLevel;
}

static void Main(string[] args) {

    //          2
    //        /   \
    //       1     3
    //      / \     \
    //     4   6     8
    //    /
    //   5
    Node root = new Node(2);
    root.left = new Node(1);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(6);
    root.right.right = new Node(8);
    root.left.left.left = new Node(5);

    Console.WriteLine(maxNodeLevel(root));
}

}

JavaScript

// JavaScript code to find Level with maximum number of nodes using BFS

class Node { constructor(x) { this.data = x; this.left = null; this.right = null; } }

// A function to find level with maximum number of nodes function maxNodeLevel(root) { if (root === null) return -1;

let q = [];
q.push(root);

let level = 0;
let maxNodes = 0;
let maxLevel = 0;

while (q.length > 0) {

    // Number of nodes at current level
    let size = q.length;

    if (size > maxNodes) {
        maxNodes = size;
        maxLevel = level;
    }

    // Process all nodes at current level
    for (let i = 0; i < size; i++) {
        let current = q.shift();

        if (current.left !== null)
            q.push(current.left);
        if (current.right !== null)
            q.push(current.right);
    }

    level++;
}

return maxLevel;

}

// 2 // /
// 1 3 // / \
// 4 6 8 // / // 5 let root = new Node(2); root.left = new Node(1); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(6); root.right.right = new Node(8); root.left.left.left = new Node(5);

console.log(maxNodeLevel(root));

`

**Using Depth First Search - O(n) time and O(n) space

The idea is to use depth-first traversal to visit each node while keeping track of its level, storing the count of nodes for each level in a hash map. As we traverse the tree recursively, we increment the counter for the current level in our map. After the entire tree is traversed, we simply identify which level has the highest node count.

Step by step approach:

1. Create a hash map to store the count of nodes for each level.
2. Perform DFS recursively, passing the current level information to each call.
3. For each node visited, increment the count for its level in the hash map.
4. After full traversal, iterate through the hash map to find the level with maximum nodes.
5. Return the level that has the highest node count. C++ `

// C++ code to find Level with maximum number of nodes using DFS #include #include using namespace std;

class Node { public: int data; Node *left, *right; Node(int x) { data = x; left = nullptr; right = nullptr; } };

// Helper function for DFS void dfs(Node* root, int level, unordered_map<int, int>& levelCount) { if (root == nullptr) return;

// Increment count of nodes at current level
levelCount[level]++;

// Recursively process left and right subtrees
dfs(root->left, level + 1, levelCount);
dfs(root->right, level + 1, levelCount);

}

int maxNodeLevel(Node *root) { if (root == nullptr) return -1;

// Map to store count of nodes at each level
unordered_map<int, int> levelCount;  

// Perform DFS to count nodes at each level
dfs(root, 0, levelCount);

int maxNodes = 0;
int maxLevel = 0;

// Find the level with maximum nodes
for (auto& pair : levelCount) {
    int level = pair.first;
    int count = pair.second;
    
    if (count > maxNodes) {
        maxNodes = count;
        maxLevel = level;
    }
}

return maxLevel;

}

int main() {

//          2
//        /   \
//       1     3
//      / \     \
//     4   6     8
//    /
//   5
Node* root = new Node(2);
root->left = new Node(1);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(6);
root->right->right = new Node(8);
root->left->left->left = new Node(5);

cout << maxNodeLevel(root) << endl;

return 0;

}

Java

// Java code to find Level with maximum number of nodes using DFS import java.util.*;

class Node { int data; Node left, right; Node(int x) { data = x; left = null; right = null; } }

class GfG {

// Helper function for DFS
static void dfs(Node root, int level, 
HashMap<Integer, Integer> levelCount) {
    if (root == null)
        return;

    // Increment count of nodes at current level
    levelCount.put(level, levelCount.getOrDefault(level, 0) + 1);

    // Recursively process left and right subtrees
    dfs(root.left, level + 1, levelCount);
    dfs(root.right, level + 1, levelCount);
}

static int maxNodeLevel(Node root) {
    if (root == null)
        return -1;

    // Map to store count of nodes at each level
    HashMap<Integer, Integer> levelCount = new HashMap<>();

    // Perform DFS to count nodes at each level
    dfs(root, 0, levelCount);

    int maxNodes = 0;
    int maxLevel = 0;

    // Find the level with maximum nodes
    for (Map.Entry<Integer, Integer> pair : levelCount.entrySet()) {
        int level = pair.getKey();
        int count = pair.getValue();

        if (count > maxNodes) {
            maxNodes = count;
            maxLevel = level;
        }
    }

    return maxLevel;
}

public static void main(String[] args) {

    //          2
    //        /   \
    //       1     3
    //      / \     \
    //     4   6     8
    //    /
    //   5
    Node root = new Node(2);
    root.left = new Node(1);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(6);
    root.right.right = new Node(8);
    root.left.left.left = new Node(5);

    System.out.println(maxNodeLevel(root));
}

}

Python

Python code to find Level with maximum number of nodes using DFS

from collections import defaultdict

class Node: def init(self, x): self.data = x self.left = None self.right = None

Helper function for DFS

def dfs(root, level, levelCount): if root is None: return

# Increment count of nodes at current level
levelCount[level] += 1

# Recursively process left and right subtrees
dfs(root.left, level + 1, levelCount)
dfs(root.right, level + 1, levelCount)

def maxNodeLevel(root): if root is None: return -1

# Map to store count of nodes at each level
levelCount = defaultdict(int)

# Perform DFS to count nodes at each level
dfs(root, 0, levelCount)

maxNodes = 0
maxLevel = 0

# Find the level with maximum nodes
for level in levelCount:
    count = levelCount[level]
    if count > maxNodes:
        maxNodes = count
        maxLevel = level

return maxLevel

if name == "main":

#          2
#        /   \
#       1     3
#      / \     \
#     4   6     8
#    /
#   5
root = Node(2)
root.left = Node(1)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(6)
root.right.right = Node(8)
root.left.left.left = Node(5)

print(maxNodeLevel(root))

C#

// C# code to find Level with maximum number of nodes using DFS using System; using System.Collections.Generic;

class Node { public int data; public Node left, right; public Node(int x) { data = x; left = null; right = null; } }

class GfG {

// Helper function for DFS
static void dfs(Node root, int level, Dictionary<int, int> levelCount) {
    if (root == null)
        return;

    // Increment count of nodes at current level
    if (!levelCount.ContainsKey(level))
        levelCount[level] = 0;
    levelCount[level]++;

    // Recursively process left and right subtrees
    dfs(root.left, level + 1, levelCount);
    dfs(root.right, level + 1, levelCount);
}

static int maxNodeLevel(Node root) {
    if (root == null)
        return -1;

    // Map to store count of nodes at each level
    Dictionary<int, int> levelCount = new Dictionary<int, int>();

    // Perform DFS to count nodes at each level
    dfs(root, 0, levelCount);

    int maxNodes = 0;
    int maxLevel = 0;

    // Find the level with maximum nodes
    foreach (var pair in levelCount) {
        int level = pair.Key;
        int count = pair.Value;

        if (count > maxNodes) {
            maxNodes = count;
            maxLevel = level;
        }
    }

    return maxLevel;
}

static void Main(string[] args) {

    //          2
    //        /   \
    //       1     3
    //      / \     \
    //     4   6     8
    //    /
    //   5
    Node root = new Node(2);
    root.left = new Node(1);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(6);
    root.right.right = new Node(8);
    root.left.left.left = new Node(5);

    Console.WriteLine(maxNodeLevel(root));
}

}

JavaScript

// JavaScript code to find Level with maximum number of nodes using DFS class Node { constructor(x) { this.data = x; this.left = null; this.right = null; } }

// Helper function for DFS function dfs(root, level, levelCount) { if (root === null) return;

// Increment count of nodes at current level
if (!levelCount.has(level)) {
    levelCount.set(level, 0);
}
levelCount.set(level, levelCount.get(level) + 1);

// Recursively process left and right subtrees
dfs(root.left, level + 1, levelCount);
dfs(root.right, level + 1, levelCount);

}

function maxNodeLevel(root) { if (root === null) return -1;

// Map to store count of nodes at each level
const levelCount = new Map();

// Perform DFS to count nodes at each level
dfs(root, 0, levelCount);

let maxNodes = 0;
let maxLevel = 0;

// Find the level with maximum nodes
for (let [level, count] of levelCount.entries()) {
    if (count > maxNodes) {
        maxNodes = count;
        maxLevel = level;
    }
}

return maxLevel;

}

// 2 // /
// 1 3 // / \
// 4 6 8 // / // 5 let root = new Node(2); root.left = new Node(1); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(6); root.right.right = new Node(8); root.left.left.left = new Node(5);

console.log(maxNodeLevel(root));

`