Level order traversal line by line (Using One Queue) (original) (raw)

Last Updated : 12 Feb, 2025

Given a **Binary Tree, the task is to print the nodes level-wise, each level on a new line.

**Example:

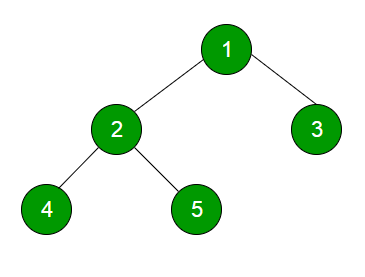
**Input:

**Output:
1
2 3
4 5

Table of Content

[Expected Approach – 1] Using Queue with delimiter – O(n) Time and O(n) Space
[Expected Approach – 2] Using Queue without delimiter – O(n) Time and O(n) Space

[Expected Approach – 1] Using Queue with delimiter – O(n) Time and O(n) Space

The idea is to use single queues anddelimiter to traverse in Level order manner.

First insert the root and a null into the queue.

NULL acts as a delimiter.

Next, pop from the top of the queue and add its left and right nodes to the end of the queue and then add the top element of the queue into container.

When we find the top element of the queue as NULL, it indicates the occurrence of next level. Continue this process till the queues become empty.

Below is the implementation of the above approach:

C++ `

// C++ Program to print level Order // traversal of Binary Tree

#include <bits/stdc++.h> using namespace std;

class Node { public: int data; Node *left, *right;

Node(int val) {
    data = val;
    left = nullptr;
    right = nullptr;
}

};

// Function to do level order traversal and // return a 2D vector vector<vector> levelOrder(Node *root) {

vector<vector<int>> result;
if (root == nullptr) return result;

queue<Node *> q;
q.push(root);
q.push(nullptr);

vector<int> currentLevel;

while (q.size() > 1) {
    Node *curr = q.front();
    q.pop();

    // Condition to check occurrence of next level.
    if (curr == nullptr) {
        result.push_back(currentLevel); 
        currentLevel.clear();           
        q.push(nullptr);                   
    } 
    else {
        currentLevel.push_back(curr->data);  

        if (curr->left) q.push(curr->left);  
        if (curr->right) q.push(curr->right); 
    }
}

if (!currentLevel.empty()) {
    result.push_back(currentLevel); 
}

return result;

}

int main() {

// Binary tree structure:
//
//        1
//       / \
//      2   3
//     / \   \
//    4   5   6


Node *root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->right->right = new Node(6);

vector<vector<int>> traversal = levelOrder(root);
for (const auto &level : traversal) {
    for (int val : level) {
        cout << val << " ";
    }
    cout << "\n";
}

return 0;

}

Java

// Java Program to print level Order // traversal of Binary Tree

import java.util.*;

class Node { int data; Node left, right;

Node(int val) {
    data = val;
    left = null;
    right = null;
}

}

class GfG {

// Function to do level order traversal and
  // return a 2D list
static ArrayList<ArrayList<Integer>> levelOrder(Node root) {
    ArrayList<ArrayList<Integer>> result = new ArrayList<>();
    if (root == null) return result;

    Queue<Node> q = new LinkedList<>();
    q.add(root);
    q.add(null);

    List<Integer> currentLevel = new ArrayList<>();

    while (q.size() > 1) {
        Node curr = q.poll();

        // Condition to check occurrence of next level.
        if (curr == null) {
            result.add(new ArrayList<>(currentLevel)); 
            currentLevel.clear();           
            q.add(null);                   
        } 
        else {
            currentLevel.add(curr.data);  

            if (curr.left != null) q.add(curr.left);  
            if (curr.right != null) q.add(curr.right); 
        }
    }

    if (!currentLevel.isEmpty()) {
        result.add(new ArrayList<>(currentLevel)); 
    }

    return result;
}

public static void main(String[] args) {

    // Binary tree structure:
    //
    //        1
    //       / \
    //      2   3
    //     / \   \
    //    4   5   6
  
    Node root = new Node(1);
    root.left = new Node(2);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(5);
    root.right.right = new Node(6);

    ArrayList<ArrayList<Integer>> traversal = levelOrder(root);
  
    for (ArrayList<Integer> level : traversal) {
        for (int val : level) {
            System.out.print(val + " ");
        }
        System.out.println();
    }
}

}

Python

Python Program to print level Order

traversal of Binary Tree

class Node: def init(self, val): self.data = val self.left = None self.right = None

Function to do level order traversal

and return a 2D list

def levelOrder(root): result = [] if root is None: return result

q = []
q.append(root)
q.append(None)

currentLevel = []

while len(q) > 1:
    curr = q.pop(0)

    # Condition to check occurrence of next level.
    if curr is None:
        result.append(currentLevel)
        currentLevel = []
        q.append(None)
    else:
        currentLevel.append(curr.data)

        if curr.left:
            q.append(curr.left)
        if curr.right:
            q.append(curr.right)

if currentLevel:
    result.append(currentLevel)

return result

if name == "main":

# Binary tree structure:
#
#        1
#       / \
#      2   3
#     / \   \
#    4   5   6
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.right = Node(6)

traversal = levelOrder(root)

for level in traversal:
    print(" ".join(map(str, level)))

C#

// C# Program to print level Order traversal // of Binary Tree

using System; using System.Collections.Generic;

class Node { public int data; public Node left, right;

public Node(int val) {
    data = val;
    left = null;
    right = null;
}

}

class GfG {

// Function to do level order traversal and return a 2D list
static List<List<int>> LevelOrder(Node root) {
    List<List<int>> result = new List<List<int>>();
    if (root == null) return result;

    Queue<Node> q = new Queue<Node>();
    q.Enqueue(root);
    q.Enqueue(null);

    List<int> currentLevel = new List<int>();

    while (q.Count > 1) {
        Node curr = q.Dequeue();

        // Condition to check occurrence of next level.
        if (curr == null) {
            result.Add(new List<int>(currentLevel)); 
            currentLevel.Clear();           
            q.Enqueue(null);                   
        } 
        else {
            currentLevel.Add(curr.data);  

            if (curr.left != null) q.Enqueue(curr.left);  
            if (curr.right != null) q.Enqueue(curr.right); 
        }
    }

    if (currentLevel.Count > 0) {
        result.Add(new List<int>(currentLevel)); 
    }

    return result;
}

static void Main(string[] args) {

    // Binary tree structure:
    //
    //        1
    //       / \
    //      2   3
    //     / \   \
    //    4   5   6
  
    Node root = new Node(1);
    root.left = new Node(2);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(5);
    root.right.right = new Node(6);

    List<List<int>> traversal = LevelOrder(root);
    foreach (var level in traversal) {
        foreach (var val in level) {
            Console.Write(val + " ");
        }
        Console.WriteLine();
    }
}

}

JavaScript

// JavaScript Program to print level Order // traversal of Binary Tree

class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } }

// Function to do level order traversal // and return a 2D array function levelOrder(root) { let result = []; if (root === null) return result;

let q = [];
q.push(root);
q.push(null);

let currentLevel = [];

while (q.length > 1) {
    let curr = q.shift();

    // Condition to check occurrence of next level.
    if (curr === null) {
        result.push(currentLevel);
        currentLevel = [];
        q.push(null);
    } else {
        currentLevel.push(curr.data);

        if (curr.left) q.push(curr.left);
        if (curr.right) q.push(curr.right);
    }
}

if (currentLevel.length > 0) {
    result.push(currentLevel);
}

return result;

}

// Binary tree structure: // // 1 // /
// 2 3 // / \
// 4 5 6

let root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.right = new Node(6);

let traversal = levelOrder(root);

for (let level of traversal) { console.log(level.join(" ")); }

**Time Complexity: O(n), where **n is the number of nodes of binary tree.
**Auxiliary Space: O(n)

[Expected Approach – 2] Using Queue without delimiter – O(n) Time and O(n) Space

To perform a level order traversal of a binary tree, use a queue to process nodes level by level.

Start by enqueuing the root node, then iterate while the queue is not empty.

For each level, determine the number of nodes to process, dequeue each node, store in the container , and enqueue its children.

After processing all nodes at the current level, finally push the current level stored in the result before moving to the next level.

Step-By-Step Implementation :

Initialize a queue, say q. Push root in q. Traverse until **q is not empty:
Create a variable **nodeCount = **q.size().
for(int i = 0; i < nodeCount; i++)
- Create temporary node node *node = q.front() and punish into the container.
- Pop front element from q.
- If **node->left != NULL push node->left in q.
- If **node->right != NULL push node->right in q.
- Push the **current level stored in the **result before moving to the next level.
Finally , return **result. C++ `

// C++ Program to print level Order traversal of Binary Tree

#include <bits/stdc++.h> using namespace std;

class Node { public: int data; Node* left; Node* right;

Node(int val) {
    data = val;
    left = nullptr;
    right = nullptr;
}

};

// Function to do level order traversal and return a 2D vector vector<vector> levelOrder(Node* root) { vector<vector> result; if (root == nullptr) return result;

// Create an empty queue for level order traversal
queue<Node*> q;
q.push(root);

while (!q.empty()) {
  
    // nodeCount (queue size) indicates number of 
      // nodes at current level.
    int nodeCount = q.size();
    vector<int> currentLevel;

    for(int i = 0; i < nodeCount; i++) {
        Node* node = q.front();
        q.pop();
        currentLevel.push_back(node->data);

        if (node->left != nullptr)
            q.push(node->left);
        if (node->right != nullptr)
            q.push(node->right);
    }
    result.push_back(currentLevel);
}

return result;

}

int main() {

// Binary tree structure:
//
//        1
//       / \
//      2   3
//     / \
//    4   5

Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);

vector<vector<int>> traversal = levelOrder(root);
for (const auto& level : traversal) {
    for (int val : level) {
        cout << val << " ";
    }
    cout << endl;
}

return 0;

}

Java

// Java Program to print level Order // traversal of Binary Tree

import java.util.ArrayList; import java.util.LinkedList; import java.util.List; import java.util.Queue;

class Node { int data; Node left, right;

Node(int val) {
    data = val;
    left = null;
    right = null;
}

}

class GfG {

// Function to do level order traversal and return a 2D list
static ArrayList<ArrayList<Integer>> levelOrder(Node root) {
    ArrayList<ArrayList<Integer>> result = new ArrayList<>();
    if (root == null) return result;

    // Create an empty queue for level order traversal
    Queue<Node> q = new LinkedList<>();
    q.add(root);

    while (!q.isEmpty()) {
      
        // nodeCount (queue size) indicates number of
          // nodes at current level.
        int nodeCount = q.size();
        ArrayList<Integer> currentLevel = new ArrayList<>();

        for(int i = 0; i < nodeCount; i++) {
            Node node = q.poll();
            currentLevel.add(node.data);

            if (node.left != null) q.add(node.left);
            if (node.right != null) q.add(node.right);
        }
        result.add(currentLevel);
    }

    return result;
}

public static void main(String[] args) {
  
    // Binary tree structure:
    //
    //        1
    //       / \
    //      2   3
    //     / \
    //    4   5
    //
  
    Node root = new Node(1);
    root.left = new Node(2);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(5);

    ArrayList<ArrayList<Integer>> traversal = levelOrder(root); 
    for (ArrayList<Integer> level : traversal) {
        for (int val : level) {
            System.out.print(val + " ");
        }
        System.out.println();
    }
}

}

Python

Python Program to print level Order

traversal of Binary Tree

class Node: def init(self, val): self.data = val self.left = None self.right = None

Function to do level order traversal

and return a 2D list

def levelOrder(root): result = [] if root is None: return result

# Create an empty queue for level order traversal
q = [root]

while q:
  
    # nodeCount (queue size) indicates number 
    # of nodes at current level.
    nodeCount = len(q)
    currentLevel = []

    for i in range(nodeCount):
        node = q.pop(0)
        currentLevel.append(node.data)

        if node.left is not None:
            q.append(node.left)
        if node.right is not None:
            q.append(node.right)

    result.append(currentLevel)

return result

if name == "main":

# Binary tree structure:
#
#        1
#       / \
#      2   3
#     / \
#    4   5
#

root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)


traversal = levelOrder(root)
for level in traversal:
    for val in level:
        print(val, end=" ")
    print()

C#

// C# Program to print level Order // traversal of Binary Tree

using System; using System.Collections.Generic;

class Node { public int data; public Node left, right;

public Node(int val) {
    data = val;
    left = null;
    right = null;
}

}

class GfG {

// Function to do level order traversal and return a 2D list
static List<List<int>> LevelOrder(Node root) {
    List<List<int>> result = new List<List<int>>();
    if (root == null) return result;

    // Create an empty queue for level order traversal
    Queue<Node> queue = new Queue<Node>();
    queue.Enqueue(root);

    while (queue.Count > 0) {
      
        // nodeCount (queue size) indicates number of
          // nodes at current level.
        int nodeCount = queue.Count;
        List<int> currentLevel = new List<int>();

        for(int i = 0; i < nodeCount; i++) {
            Node node = queue.Dequeue();
            currentLevel.Add(node.data);

            if (node.left != null) queue.Enqueue(node.left);
            if (node.right != null) queue.Enqueue(node.right);
        }
        result.Add(currentLevel);
    }

    return result;
}

static void Main(string[] args) {
  
    // Binary tree structure:
    //
    //        1
    //       / \
    //      2   3
    //     / \
    //    4   5
  
    Node root = new Node(1);
    root.left = new Node(2);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(5);

    List<List<int>> traversal = LevelOrder(root);
    foreach (List<int> level in traversal) {
        foreach (int val in level) {
            Console.Write(val + " ");
        }
        Console.WriteLine();
    }
}

}

JavaScript

// JavaScript Program to print level Order // traversal of Binary Tree

class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } }

// Function to do level order traversal and return a 2D array function levelOrder(root) { const result = []; if (root === null) return result;

// Create an empty queue for level order traversal
const q = [root];

while (q.length > 0) {

    // nodeCount (queue size) indicates number 
    // of nodes at current level.
    const nodeCount = q.length;
    const currentLevel = [];

    for (let i = 0; i < nodeCount; i++) {
        const node = q.shift();
        currentLevel.push(node.data);

        if (node.left !== null) q.push(node.left);
        if (node.right !== null) q.push(node.right);
    }

    result.push(currentLevel);
}

return result;

}

// Binary tree structure: // 1 // /
// 2 3 // /
// 4 5

const root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5);

const traversal = levelOrder(root); for (const level of traversal) { console.log(level.join(" ")); }

**Time complexity: O(n), where n is number of nodes of binary tree.
**Auxiliary Space: O(n)

**Related articles:

Level Order Traversal (Breadth First Search or BFS) of Binary Tree

Print level order traversal line by line