Longest Increasing Subsequence (LIS) (original) (raw)
Last Updated : 03 Mar, 2025
Given an array **arr[] of size **n, the task is to find the **length of the **Longest Increasing Subsequence (LIS) i.e., the longest possible subsequence in which the elements of the subsequence are **sorted in **increasing order.
**Examples:
**Input: arr[] = [3, 10, 2, 1, 20]
**Output: 3
**Explanation: The longest increasing subsequence is 3, 10, 20**Input: arr[] = [30, 20, 10]
****Output:**1
**Explanation: The longest increasing subsequences are [30], [20] and [10]**Input: arr[] = [2, 2, 2]
**Output: 1
**Explanation: We consider only strictly increasing.**Input: arr[] = [10, 20, 35, 80]
**Output: 4
**Explanation: The whole array is sorted
Table of Content
- [Naive Approach] Using Recursion - Exponential Time and Linear Space
- [Better Approach - 1] Using Memoization - O(n^2) Time and O(n) Space
- [Better Approach - 2] Using DP (Bottom Up Tabulation) - O(n^2) Time and O(n) Space
- [Expected Approach] Using Binary Search - O(n Log n) Time and O(n) Space
- Problems based on LIS
[Naive Approach] Using Recursion - Exponential Time and Linear Space
The idea to do traverse the input array from left to right and find lengthof the Longest Increasing Subsequence (LIS) ending with every element **arr[i]. Let the length found for arr[i] be **L[i]. At the end we return maximum of all L[i] values. Now to compute L[i], we use recursion, we consider all smaller elements onleft of arr[i], recursively compute LIS value for all the smaller elements on left, take the **maximum of all and **add 1 to it. If there is no smaller element on left of an element, we **return 1.
Let L(i) be the **length of the LIS ending at index i such that **arr[i] is the last element of the LIS. Then, L(i) can be recursively written as:
- **L(i) = 1 + max(L(prev) ) where 0 < **prev < i and arr[prev] < arr[i]; or
- **L(i) = 1, if no such prev exists.
Formally, the length of LIS ending at index **i, is 1 greater than the maximum of lengths of all LIS ending at some index **prev such that **arr[prev] < arr[i] where prev < i.
After we fill the L array, we find LIS as maximum of all in L[]
Overall LIS = max(L[i]) where 0 <= i < n
We can see that the above recurrence relation follows the **optimal substructure property. Follow the below illustration to see overlapping subproblems.
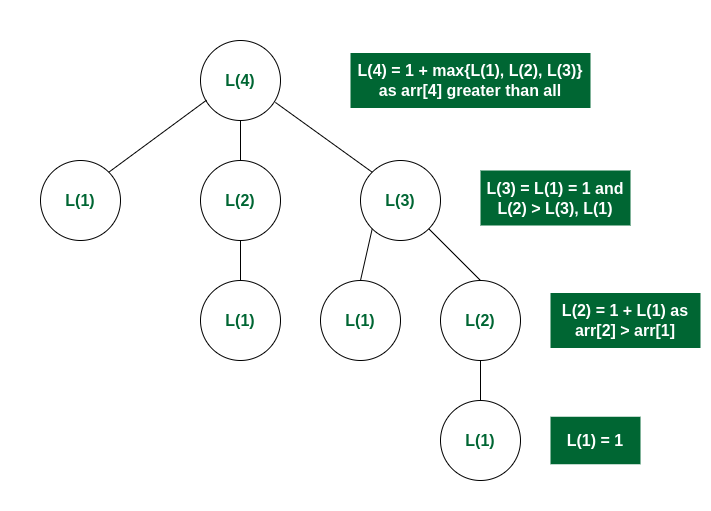
Consider arr[] = [3, 10, 2, 11]
**L(i): Denotes LIS of subarray ending at position 'i'
Recursion Tree
C++ `
// Cpp program to find lis using recursion // in Exponential Time and Linear Space #include <bits/stdc++.h> using namespace std;
// Returns LIS of subarray ending with index i. int lisEndingAtIdx(vector& arr, int idx) {
// Base case
if (idx == 0)
return 1;
// Consider all elements on the left of i,
// recursively compute LISs ending with
// them and consider the largest
int mx = 1;
for (int prev = 0; prev < idx; prev++)
if (arr[prev] < arr[idx])
mx = max(mx, lisEndingAtIdx(arr, prev) + 1);
return mx;}
int lis(vector& arr) { int n = arr.size(); int res = 1; for (int i = 1; i < n; i++) res = max(res, lisEndingAtIdx(arr, i)); return res; }
int main() { vector arr = { 10, 22, 9, 33, 21, 50, 41, 60 }; cout << lis(arr); return 0; }
Java
// Java program to find lis using recursion // in Exponential Time and Linear Space import java.util.*;
class GfG { static int lisEndingAtIdx(int[] arr, int idx) {
// Base case
if (idx == 0)
return 1;
// Consider all elements on the left of i,
// recursively compute LISs ending with
// them and consider the largest
int mx = 1;
for (int prev = 0; prev < idx; prev++)
if (arr[prev] < arr[idx])
mx = Math.max(mx, lisEndingAtIdx(arr, prev) + 1);
return mx;
}
static int lis(int[] arr) {
int n = arr.length;
int res = 1;
for (int idx = 1; idx < n; idx++)
res = Math.max(res, lisEndingAtIdx(arr, idx));
return res;
}
public static void main(String[] args) {
int[] arr = { 10, 22, 9, 33, 21, 50, 41, 60 };
System.out.println(lis(arr));
}}
Python
Python program to find lis using recursion
in Exponential Time and Linear Space
def lisEndingAtIdx(arr, idx):
# Base case
if idx == 0:
return 1
# Consider all elements on the left of i,
# recursively compute LISs ending with
# them and consider the largest
mx = 1
for prev in range(idx):
if arr[prev] < arr[idx]:
mx = max(mx, lisEndingAtIdx(arr, prev) + 1)
return mxdef lis(arr): n = len(arr) res = 1 for idx in range(1, n): res = max(res, lisEndingAtIdx(arr, idx)) return res
if name == "main": arr = [10, 22, 9, 33, 21, 50, 41, 60] print(lis(arr))
C#
// C# program to find lis using recursion // in Exponential Time and Linear Space using System; using System.Collections.Generic;
class GfG { static int lisEndingAtIdx(List arr, int idx) { // Base case if (idx == 0) return 1;
// Consider all elements on the left of i,
// recursively compute LISs ending with
// them and consider the largest
int mx = 1;
for (int prev = 0; prev < idx; prev++)
if (arr[prev] < arr[idx])
mx = Math.Max(mx, lisEndingAtIdx(arr, prev) + 1);
return mx;
}
static int lis(List<int> arr) {
int n = arr.Count;
int res = 1;
for (int idx = 1; idx < n; idx++)
res = Math.Max(res, lisEndingAtIdx(arr, idx));
return res;
}
static void Main(string[] args) {
List<int> arr = new List<int> { 10, 22, 9, 33, 21, 50, 41, 60 };
Console.WriteLine(lis(arr));
}}
JavaScript
// JavaScript program to find lis using recursion // in Exponential Time and Linear Space function lisEndingAtIdx(arr, idx) {
// Base case
if (idx === 0)
return 1;
// Consider all elements on the left of i,
// recursively compute LISs ending with
// them and consider the largest
let mx = 1;
for (let prev = 0; prev < idx; prev++) {
if (arr[prev] < arr[idx]) {
mx = Math.max(mx,
lisEndingAtIdx(arr, prev) + 1);
}
}
return mx;}
function lis(arr) { let n = arr.length; let res = 1; for (let idx = 1; idx < n; idx++) { res = Math.max(res, lisEndingAtIdx(arr, idx)); } return res; }
let arr = [ 10, 22, 9, 33, 21, 50, 41, 60 ]; console.log(lis(arr));
`
[Better Approach - 1] Using Memoization - O(n^2) Time and O(n) Space
If notice carefully, we can see that the above **recursive function lisEndingAtIdx() also follows the **overlapping subproblems property i.e., same substructure solved again and again in different recursion call paths. We can avoid this using the memoization approach. Since there is only **one parameter that changes in recursive calls and the range of the parameter goes from **0 to n-1, so we us a 1D array of size n and initialize it as -1 to indicate that the values are not computed yet.
C++ `
#include <bits/stdc++.h> using namespace std;
int lisEndingAtIdx(vector& arr, int idx, vector& memo) {
// Base case
if (idx == 0)
return 1;
// Check if the result is already computed
if (memo[idx] != -1)
return memo[idx];
// Consider all elements on left of i,
// recursively compute LISs ending with
// them and consider the largest
int mx = 1;
for (int prev = 0; prev < idx; prev++)
if (arr[prev] < arr[idx])
mx = max(mx, lisEndingAtIdx(arr, prev, memo) + 1);
// Store the result in the memo array
memo[idx] = mx;
return memo[idx];}
int lis(vector& arr) {
int n = arr.size();
vector<int> memo(n, -1);
int res = 1;
for (int i = 1; i < n; i++)
res = max(res, lisEndingAtIdx(arr, i, memo));
return res;}
int main() { vector arr = { 10, 22, 9, 33, 21, 50, 41, 60 }; cout << lis(arr); return 0; }
Java
import java.util.*;
class GfG { static int lisEndingAtIdx(int[] arr, int idx, int[] memo) {
// Base case
if (idx == 0)
return 1;
// Check if the result is already computed
if (memo[idx] != -1)
return memo[idx];
// Consider all elements on left of i,
// recursively compute LISs ending with
// them and consider the largest
int mx = 1;
for (int prev = 0; prev < idx; prev++)
if (arr[prev] < arr[idx])
mx = Math.max(mx, lisEndingAtIdx(arr, prev, memo) + 1);
// Store the result in the memo array
memo[idx] = mx;
return memo[idx];
}
static int lis(int[] arr) {
int n = arr.length;
int[] memo = new int[n];
Arrays.fill(memo, -1);
int res = 1;
for (int idx = 1; idx < n; idx++)
res = Math.max(res, lisEndingAtIdx(arr, idx, memo));
return res;
}
public static void main(String[] args) {
int[] arr = {10, 22, 9, 33, 21, 50, 41, 60};
System.out.println(lis(arr));
}}
Python
def lisEndingAtIdx(arr, idx, memo):
# Base case
if idx == 0:
return 1
# Check if the result is already computed
if memo[idx] != -1:
return memo[idx]
# Consider all elements on left of i,
# recursively compute LISs ending with
# them and consider the largest
mx = 1
for prev in range(idx):
if arr[prev] < arr[idx]:
mx = max(mx, lisEndingAtIdx(arr, prev, memo) + 1)
# Store the result in the memo array
memo[idx] = mx
return memo[idx]def lis(arr): n = len(arr)
memo = [-1] * n
res = 1
for idx in range(1, n):
res = max(res, lisEndingAtIdx(arr, idx, memo))
return resif name == "main": arr = [10, 22, 9, 33, 21, 50, 41, 60] print(lis(arr))
C#
using System; using System.Collections.Generic;
class GfG { static int lisEndingAtIdx(List arr, int idx, int[] memo) {
// Base case
if (idx == 0)
return 1;
// Check if the result is already computed
if (memo[idx] != -1)
return memo[idx];
// Consider all elements on left of i,
// recursively compute LISs ending with
// them and consider the largest
int mx = 1;
for (int prev = 0; prev < idx; prev++)
if (arr[prev] < arr[idx])
mx = Math.Max(mx, lisEndingAtIdx(arr, prev, memo) + 1);
// Store the result in the memo array
memo[idx] = mx;
return memo[idx];
}
static int lis(List<int> arr) {
int n = arr.Count;
int[] memo = new int[n];
for(int i = 0; i < n; i++) {
memo[i] = -1;
}
int res = 1;
for (int idx = 1; idx < n; idx++)
res = Math.Max(res, lisEndingAtIdx(arr, idx, memo));
return res;
}
static void Main(string[] args) {
List<int> arr = new List<int> {10, 22, 9, 33, 21, 50, 41, 60};
Console.WriteLine(lis(arr));
}}
JavaScript
function lisEndingAtIdx(arr, idx, memo) {
// Base case
if (idx === 0)
return 1;
// Check if the result is already computed
if (memo[idx] !== -1)
return memo[idx];
// Consider all elements on left of i,
// recursively compute LISs ending with
// them and consider the largest
let mx = 1;
for (let prev = 0; prev < idx; prev++) {
if (arr[prev] < arr[idx]) {
mx = Math.max(
mx, lisEndingAtIdx(arr, prev, memo) + 1);
}
}
// Store the result in the memo array
memo[idx] = mx;
return memo[idx];}
function lis(arr) { const n = arr.length;
const memo = Array(n).fill(-1);
let res = 1;
for (let idx = 1; idx < n; idx++) {
res = Math.max(res, lisEndingAtIdx(arr, idx, memo));
}
return res;}
const arr = [ 10, 22, 9, 33, 21, 50, 41, 60 ]; console.log(lis(arr));
`
[Better Approach - 2] Using DP (Bottom Up Tabulation) - O(n^2) Time and O(n) Space
The **tabulation approach for finding the **Longest Increasing Subsequence (LIS) solves the problem iteratively in a **bottom-up manner. The idea is to maintain a **1D array lis[], where **lis[i] stores the length of the longest increasing subsequence that **ends at index i. Initially, each element in lis[] is set to 1, as the smallest possible subsequence for any element is the element itself.
The algorithm then iterates over each element of the array. For each element **arr[i], it checks all **previous elements arr[0] to arr[i-1]. If **arr[i] is greater than arr[prev] (ensuring the subsequence is increasing), it updates **lis[i] to the maximum of its current value or lis[prev] + 1, indicating that we can extend the subsequence ending at **arr[prev] by **including arr[i].
Finally, the **length of the longest increasing subsequence is the maximum value in the lis[] array.
C++ `
#include <bits/stdc++.h> using namespace std;
// lis() returns the length of the longest // increasing subsequence in arr of size n int lis(vector& arr) { int n = arr.size(); vector lis(n, 1);
// Compute optimized LIS values in
// bottom-up manner
for (int i = 1; i < n; i++) {
for (int prev = 0; prev < i; prev++) {
if (arr[i] > arr[prev] && lis[i] < lis[prev] + 1) {
lis[i] = lis[prev] + 1;
}
}
}
// Return maximum value in lis
return *max_element(lis.begin(), lis.end());}
int main() { vector arr = { 10, 22, 9, 33, 21, 50, 41, 60 }; cout << lis(arr) << endl; return 0; }
Java
import java.lang.*;
class GfG {
// lis() returns the length of the longest
// increasing subsequence in arr[] of size n
static int lis(int arr[]) {
int n = arr.length;
int lis[] = new int[n];
// Initialize LIS values for all indexes
for (int i = 0; i < n; i++)
lis[i] = 1;
// Compute optimized LIS values in
// bottom up manner
for (int i = 1; i < n; i++)
for (int prev = 0; prev < i; prev++)
if (arr[i] > arr[prev] && lis[i] < lis[prev] + 1)
lis[i] = lis[prev] + 1;
// Pick maximum of all LIS values
int max = 1;
for (int i = 0; i < n; i++)
max = Math.max(max, lis[i]);
return max;
}
public static void main(String args[]) {
int arr[] = { 10, 22, 9, 33, 21, 50, 41, 60 };
System.out.println(lis(arr));
}}
Python
lis returns length of the longest
increasing subsequence in arr of size n
def lis(arr): n = len(arr)
# Declare the list (array) for LIS and
# initialize LIS values for all indexes
lis = [1] * n
# Compute optimized LIS values in bottom
# -up manner
for i in range(1, n):
for prev in range(0, i):
if arr[i] > arr[prev]:
lis[i] = max(lis[i], lis[prev] + 1)
# Return the maximum of all LIS values
return max(lis)if name == 'main': arr = [10, 22, 9, 33, 21, 50, 41, 60] print(lis(arr))
C#
using System;
class GfG {
// lis() returns the length of the longest
// increasing subsequence in arr[] of size n
static int lis(int[] arr) {
int n = arr.Length;
int[] lis = new int[n];
// Initialize LIS values for all indexes
for (int i = 0; i < n; i++)
lis[i] = 1;
// Compute optimized LIS values in bottom up manner
for (int i = 1; i < n; i++) {
for (int prev = 0; prev < i; prev++) {
if (arr[i] > arr[prev] && lis[i] < lis[prev] + 1)
lis[i] = lis[prev] + 1;
}
}
// Pick maximum of all LIS values
int max = 0;
for (int i = 0; i < n; i++) {
if (max < lis[i])
max = lis[i];
}
return max;
}
static void Main() {
int[] arr = { 10, 22, 9, 33, 21, 50, 41, 60 };
Console.WriteLine(lis(arr));
}}
JavaScript
// lis() returns the length of the longest // increasing subsequence in arr[] of size n function lis(arr) { let n = arr.length;
let lis = Array(n).fill(0);
let max = 0;
// Initialize LIS values for all indexes
for (let i = 0; i < n; i++)
lis[i] = 1;
// Compute optimized LIS values in
// bottom up manner
for (let i = 1; i < n; i++) {
for (let prev = 0; prev < i; prev++) {
if (arr[i] > arr[prev] && lis[i] < lis[prev] + 1)
lis[i] = lis[prev] + 1;
}
}
// Pick maximum of all LIS values
for (let i = 0; i < n; i++)
if (max < lis[i])
max = lis[i];
return max;}
let arr = [10, 22, 9, 33, 21, 50, 41, 60]; console.log(lis(arr));
`
[Expected Approach] **Using Binary Search - O(n Log n) Time and O(n) Space
We can solve this in **O(n Log n) time using Binary Search. The idea is to traverse the given sequence and maintain a separate list of **sorted subsequence so far. For every new element, find its position in the sorted subsequence using Binary Search.
Refer Longest Increasing Subsequence Size (N * logN) for details.