Minimum swap required to convert binary tree to binary search tree (original) (raw)
Last Updated : 25 Nov, 2024
Given an array **arr[] which represents a Complete Binary Tree i.e., if **index i is the **parent, index **2*i + 1 is the left child and index 2*i + 2 is **the right child. The task is to find the **minimum number of **swaps required to convert it into a **Binary Search Tree.
**Examples:
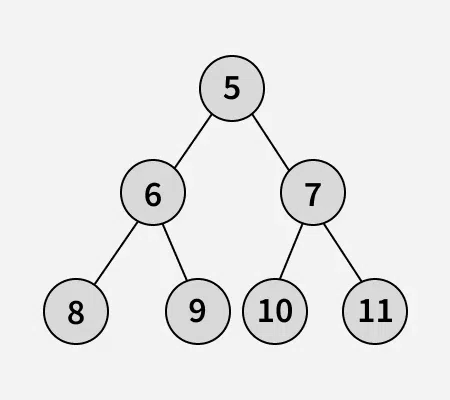
**Input: arr[] = [5, 6, 7, 8, 9, 10, 11]
**Output: 3
**Explanation:
Binary tree of the given array:
Swap 1: Swap node 8 with node 5.
Swap 2: Swap node 9 with node 10.
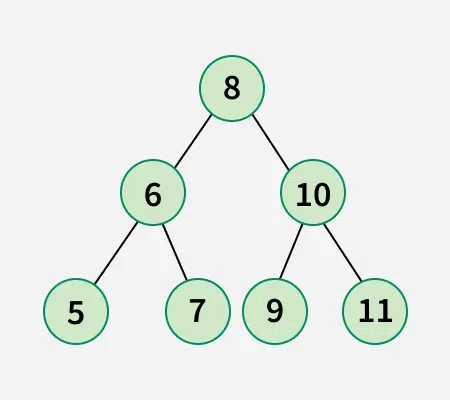
Swap 3: Swap node 10 with node 7.So, minimum 3 swaps are required to obtain the below binary search tree:
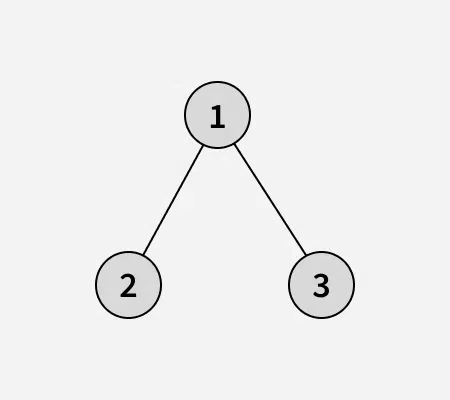
**Input: arr[] = [1, 2, 3]
**Output: 1
**Explanation:
Binary tree of the given array:
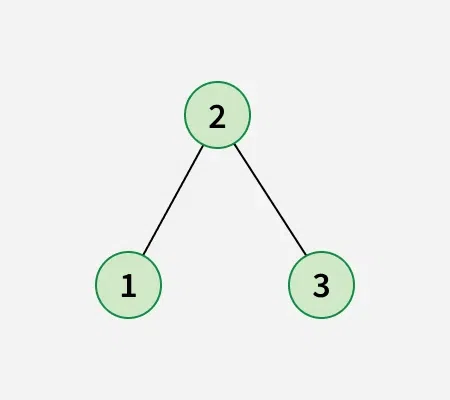
After swapping node 1 with node 2, obtain the below binary search tree:
**Approach:
The idea is to use the fact that **inorder traversalof **Binary Search Tree is in **increasing order of their value.
So, find the inorder traversal of the Binary Tree and **store it in the array and try to **sort the array. Theminimum number of swap required to get the array sorted will be the answer.
C++ `
// C++ program for Minimum swap required // to convert binary tree to binary search tree
#include<bits/stdc++.h> using namespace std;
// Function to perform inorder traversal of the binary tree // and store it in vector v void inorder(vector& arr, vector& inorderArr, int index) {
int n = arr.size();
// If index is out of bounds, return
if (index >= n)
return;
// Recursively visit left subtree
inorder(arr, inorderArr, 2 * index + 1);
// Store current node value in vector
inorderArr.push_back(arr[index]);
// Recursively visit right subtree
inorder(arr, inorderArr, 2 * index + 2);}
// Function to calculate minimum swaps // to sort inorder traversal int minSwaps(vector& arr) { int n = arr.size(); vector inorderArr;
// Get the inorder traversal of the binary tree
inorder(arr, inorderArr, 0);
// Create an array of pairs to store value
// and original index
vector<pair<int, int>> t(inorderArr.size());
int ans = 0;
// Store the value and its index
for (int i = 0; i < inorderArr.size(); i++)
t[i] = {inorderArr[i], i};
// Sort the pair array based on values
// to get BST order
sort(t.begin(), t.end());
// Find minimum swaps by detecting cycles
for (int i = 0; i < t.size(); i++) {
// If the element is already in the
// correct position, continue
if (i == t[i].second)
continue;
// Otherwise, perform swaps until the element
// is in the right place
else {
// Swap elements to correct positions
swap(t[i].first, t[t[i].second].first);
swap(t[i].second, t[t[i].second].second);
}
// Check if the element is still not
// in the correct position
if (i != t[i].second)
--i;
// Increment swap count
ans++;
}
return ans;}
int main() {
vector<int> arr = { 5, 6, 7, 8, 9, 10, 11 };
cout << minSwaps(arr) << endl;}
Java
// Java program for Minimum swap required // to convert binary tree to binary search tree import java.util.Arrays;
class GfG {
// Function to perform inorder traversal of the binary tree
// and store it in an array
static void inorder(int[] arr, int[] inorderArr,
int index, int[] counter) {
int n = arr.length;
// Base case: if index is out of bounds, return
if (index >= n)
return;
// Recursively visit left subtree
inorder(arr, inorderArr, 2 * index + 1, counter);
// Store current node value in the inorder array
inorderArr[counter[0]] = arr[index];
counter[0]++;
// Recursively visit right subtree
inorder(arr, inorderArr, 2 * index + 2, counter);
}
// Function to calculate minimum swaps
// to sort inorder traversal
static int minSwaps(int[] arr) {
int n = arr.length;
int[] inorderArr = new int[n];
int[] counter = new int[1];
// Get the inorder traversal of the binary tree
inorder(arr, inorderArr, 0, counter);
// Create an array of pairs to store the value
// and its original index
int[][] t = new int[n][2];
int ans = 0;
// Store the value and its original index
for (int i = 0; i < n; i++) {
t[i][0] = inorderArr[i];
t[i][1] = i;
}
// Sort the array based on values to get BST order
Arrays.sort(t, (a, b) -> Integer.compare(a[0], b[0]));
// Find minimum swaps by detecting cycles
boolean[] visited = new boolean[n];
// Iterate through the array to find cycles
for (int i = 0; i < n; i++) {
// If the element is already visited or in
// the correct place, continue
if (visited[i] || t[i][1] == i)
continue;
// Start a cycle and find the number of
// nodes in the cycle
int cycleSize = 0;
int j = i;
while (!visited[j]) {
visited[j] = true;
j = t[j][1];
cycleSize++;
}
// If there is a cycle, we need (cycleSize - 1)
// swaps to sort the cycle
if (cycleSize > 1) {
ans += (cycleSize - 1);
}
}
// Return the total number of swaps
return ans;
}
public static void main(String[] args) {
int[] arr = {5, 6, 7, 8, 9, 10, 11};
System.out.println(minSwaps(arr));
}}
` Python ``
Python program for Minimum swap required
to convert binary tree to binary search tree
Function to perform inorder traversal of the binary tree
and store it in an array
def inorder(arr, inorderArr, index):
# If index is out of bounds, return
n = len(arr)
if index >= n:
return
# Recursively visit left subtree
inorder(arr, inorderArr, 2 * index + 1)
# Store current node value in inorderArr
inorderArr.append(arr[index])
# Recursively visit right subtree
inorder(arr, inorderArr, 2 * index + 2)Function to calculate minimum swaps
to sort inorder traversal
def minSwaps(arr): inorderArr = []
# Get the inorder traversal of the binary tree
inorder(arr, inorderArr, 0)
# Create a list of pairs to store value and original index
t = [(inorderArr[i], i) for i in range(len(inorderArr))]
ans = 0
# Sort the list of pairs based on values
# to get BST order
t.sort()
# Initialize visited array
visited = [False] * len(t)
# Find minimum swaps by detecting cycles
for i in range(len(t)):
# If already visited or already in the
# correct place, skip
if visited[i] or t[i][1] == i:
continue
# Start a cycle and find the number of
# nodes in the cycle
cycleSize = 0
j = i
# Process all elements in the cycle
while not visited[j]:
visited[j] = True
j = t[j][1]
cycleSize += 1
# If there is a cycle of size `cycle_size`, we
# need `cycle_size - 1` swaps
if cycleSize > 1:
ans += (cycleSize - 1)
# Return total number of swaps
return ansif name == "main": arr = [5, 6, 7, 8, 9, 10, 11] print(minSwaps(arr))
C#
// C# program for Minimum swap required // to convert binary tree to binary search tree using System; using System.Linq;
class GfG {
// Function to perform inorder traversal of the binary tree
// and store it in an array
static void Inorder(int[] arr, int[] inorderArr, int index, ref int counter) {
int n = arr.Length;
// Base case: if index is out of bounds, return
if (index >= n)
return;
// Recursively visit left subtree
Inorder(arr, inorderArr, 2 * index + 1, ref counter);
// Store current node value in inorderArr
inorderArr[counter] = arr[index];
counter++;
// Recursively visit right subtree
Inorder(arr, inorderArr, 2 * index + 2, ref counter);
}
// Function to calculate minimum
// swaps to sort inorder traversal
static int MinSwaps(int[] arr) {
int n = arr.Length;
int[] inorderArr = new int[n];
int counter = 0;
// Get the inorder traversal of the binary tree
Inorder(arr, inorderArr, 0, ref counter);
// Create an array of pairs to store value
// and original index
var t = new (int, int)[n];
for (int i = 0; i < n; i++) {
t[i] = (inorderArr[i], i);
}
// Sort the array based on values to get BST order
Array.Sort(t, (a, b) => a.Item1.CompareTo(b.Item1));
// Initialize visited array
bool[] visited = new bool[n];
int ans = 0;
// Find minimum swaps by detecting cycles
for (int i = 0; i < n; i++) {
// If already visited or already in
// the correct place, skip
if (visited[i] || t[i].Item2 == i)
continue;
// Start a cycle and find the number
// of nodes in the cycle
int cycleSize = 0;
int j = i;
// Process all elements in the cycle
while (!visited[j]) {
visited[j] = true;
j = t[j].Item2;
cycleSize++;
}
// If there is a cycle of size `cycle_size`, we
// need `cycle_size - 1` swaps
if (cycleSize > 1)
{
ans += (cycleSize - 1);
}
}
// Return total number of swaps
return ans;
}
static void Main(string[] args) {
int[] arr = { 5, 6, 7, 8, 9, 10, 11 };
Console.WriteLine(MinSwaps(arr));
}}
`` JavaScript `
// Javascript program for Minimum swap required // to convert binary tree to binary search tree
// Inorder traversal to get values in sorted order function inorder(arr, inorderArr, index) {
// If index is out of bounds, return
if (index >= arr.length)
return;
// Recursively visit left subtree
inorder(arr, inorderArr, 2 * index + 1);
// Store current node value in array
inorderArr.push(arr[index]);
// Recursively visit right subtree
inorder(arr, inorderArr, 2 * index + 2);}
// Function to calculate minimum swaps to sort inorder // traversal function minSwaps(arr) {
let inorderArr = [];
// Get the inorder traversal of the binary tree
inorder(arr, inorderArr, 0);
// Create an array of pairs to store value and original
// index
let t = inorderArr.map((val, i) => [val, i]);
let ans = 0;
// Sort the pair array based on values to get BST order
t.sort((a, b) => a[0] - b[0]);
// Find minimum swaps by detecting cycles
let visited = Array(arr.length)
.fill(false);
for (let i = 0; i < t.length; i++) {
// If the element is already in the correct
// position, continue
if (visited[i] || t[i][1] === i)
continue;
// Otherwise, perform swaps until the element is in
// the right place
let cycleSize = 0;
let j = i;
while (!visited[j]) {
visited[j] = true;
j = t[j][1];
cycleSize++;
}
// If there is a cycle, we need (cycleSize - 1)
// swaps to sort the cycle
if (cycleSize > 1) {
ans += (cycleSize - 1);
}
}
// Return total number of swaps
return ans;}
let arr = [ 5, 6, 7, 8, 9, 10, 11 ]; console.log(minSwaps(arr));
`
**Time Complexity: O(n*logn) where n is the number of elements in array.
**Auxiliary Space: O(n) because it is using extra space for array
**Exercise: Can we extend this to normal binary tree, i.e., a binary tree represented using left and right pointers, and not necessarily complete?