numpy.absolute() in Python (original) (raw)

Last Updated : 29 Nov, 2018

numpy.absolute(arr, out = None, ufunc ‘absolute’) : This mathematical function helps user to calculate absolute value of each element. For complex input, a + ib, the absolute value is 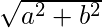\sqrt { a^2 + b^2 }.Parameters :

arr : [arraylike] Input array or object whose elements, we need to test.

Return :

An array with absolute value of each array.

Code #1 : Working

import numpy as np

arr1 = [ 1 , - 3 , 15 , - 466 ]

print ( "Absolute Value of arr1 : \n" ,

`` np.absolute(arr1))

arr2 = [ 23 , - 56 ]

print ( "\nAbsolute Value of arr2 : \n" ,

`` np.absolute(arr2))

Output :

Absolute Value of arr1 : [ 1 3 15 466]

Absolute Value of arr2 : [23 56]

Code #2 : Working with complex numbers

import numpy as np

a = 4 + 3j

print ( "Absolute(4 + 3j) : " ,

`` np.absolute(a))

b = 16 + 13j

print ( "\nAbsolute value(16 + 13j) : " ,

`` np.absolute(b))

Output :

Absolute(4 + 3j) : 5.0

Absolute value(16 + 13j) : 20.6155281281

Code #3: Graphical Representation of numpy.absolute()

import numpy as np

import matplotlib.pyplot as plt

a = np.linspace(start = - 5 , stop = 5 ,

`` num = 6 , endpoint = True )

print ( "Graphical Representation : \n" ,

`` np.absolute(a))

plt.title( "blue : with absolute\nred : without absolute" )

plt.plot(a, np.absolute(a))

plt.plot(a, a, color = 'red' )

plt.show()

Output :

Graphical Representation : [ 5. 3. 1. 1. 3. 5.]

References : https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.absolute.html.

Similar Reads