One Dimensional Array in Java (original) (raw)
Last Updated : 28 May, 2025
An **array is a type of **data structure that can store a collection of elements. These elements are stored in contiguous memory locations and provide efficient access to each element based on the index of each array element.
In this article, we will learn about a **one-dimensional array in Java.
What is an Array?
Arrays are commonly used for storing and manipulating data in programming languages because they offer fast access to the elements based on their indices and provide efficient memory usage.
**Syntax
dataType [] arrayName = new dataType [arraySize] ;
One-Dimensional Array
One of the most commonly used types of arrays is the one-dimensional array. It represents a simple list of elements where each item can be accessed using a single index.
**Note: To know how to declare and initialize an array, refer to this article: Declare and Initialize an Array in Java
Example of a One-Dimensional Array
Below is an example demonstrating a one-dimensional array in Java:
Java `
// Java Program to implement // One-Dimensional Array
// Driver Class public class Geeks {
// Main Function
public static void main(String[] args)
{
// Declare and initialize an array of integers
int[] numbers = { 10, 20, 30, 40, 50 };
System.out.println("Original Array:");
printArray(numbers);
// Accessing elements of the array
System.out.println("\nElement at index 2: "
+ numbers[2]);
// Modifying an element of the array
numbers[3] = 45;
System.out.println("\nModified Array:");
printArray(numbers);
// Calculating the sum of elements in the array
int sum = calculateSum(numbers);
System.out.println("\nSum of elements in the array: "
+ sum);
}
// Method to print the elements of an array
public static void printArray(int[] arr)
{
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
// Method to calculate the sum of elements in an array
public static int calculateSum(int[] arr)
{
int sum = 0;
for (int num : arr) {
sum += num;
}
return sum;
}}
`
Output
Original Array: 10 20 30 40 50
Element at index 2: 30
Modified Array: 10 20 30 45 50
Sum of elements in the array: 155
Memory Organization of a One-Dimensional Array
In memory, a one-dimensional array in Java is a c**ontiguous block of the memory locations allocated to the hold elements of the same data type. Each element occupies a fixed amount of memory determined by the data type of array. The elements in the array are stored sequentially in the memory by the one by one.
**Example:
int [ ] numbers = new int [5] ;
The memory organization as shown below: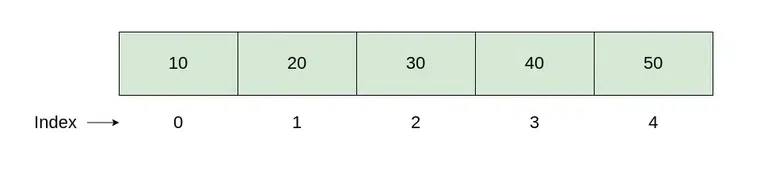
- In the above diagram, 10, 20, 30, 40, 50 are represents the individual elements of the array.
- The length of the array is 5. The length of array is count from 1.
- The index of the array is count from 0.
- Each element is stored at the specific index starting from the 0 and going up to the [size-1].
- The memory addresses are allocated for the each element are contiguous, meaning they are adjacent to the each other in the memory.
Basic Operations on One-Dimensional Array
Basic operations on a one-dimensional array is include the **accessing elements, inserting elements, deleting elements, searching for elements and sorting elements. Below are the basic operations performed on a one-dimensional array with the time complexity and space complexity:
| Operations | Description | Complexity |
|---|---|---|
| Accessing Elements | Accessing elements in an array involved the retrieving values and stored at a specific index. | Time Complexity: O(1)Space Complexity:O(1) |
| Inserting Elements | Inserting an element into array is involved the adding a new value at the specific index or at end of the array. If the array is filled, it will may be required resizing. | Time Complexity:O(1): If inserting at the end of the array without resizing the array.O(n): If inserting at the specific index or at the end of array with resizing, where n is the number of the elements in array. Space Complexity:O(1): If the array is no need to resize.O(n): If the array is required to resize, here n is the number of elements of array. |
| Deleting Elements | Deleting element from an array is involve the removing a value from the specific index and shifting subsequent elements to fill gap in an array. | Time Complexity: O(n)Space Complexity: O(1) |
| Searching for Elements | Searching for specific element in an array is involve traversing the array for find the element in an array. | Time Complexity:O(n): Linear time complexity for the sequential search, the worst-case scenario involved the traversing the entire array.O(log n): If the array is binary search is used and sorted, where n is the number of the elements in an array.Space Complexity: O(1): Constant space complexity as no additional memory is required. |
| Sorting Elements | Sorting elements in an array is involve arranging the elements in the specific order such as ascending order or descending order. | Time Complexity:O(n^2): Quadratic time complexity for the inefficient sorting algorithms such as bubble sort or selection sort.O(n log n): Average time complexity for the efficient sorting algorithms such as merge sort, heap sort or quick sort.Space Complexity:O(1): If the sorting algorithm is an in-place algorithm that doesn't require the extra space.O(n): If the additional space is required for the sorting such as merge sort. |
Implementation of One-Dimensional Array in Java
This Java program demonstrates the implementation of the one-dimensional array and it performs the basic operations like initialization, accessing elements, inserting elements, deleting elements, searching for elements and sorting elements:
Java `
// Java Program to implement // One Dimensional Array import java.util.Arrays;
// Driver Class public class Geeks {
// Main Function
public static void main(String[] args)
{
// Initializing an array
int[] numbers = new int[5];
// Inserting elements into the array
numbers[0] = 10;
numbers[1] = 30;
numbers[2] = 20;
numbers[3] = 50;
numbers[4] = 40;
// Accessing elements in the array
System.out.println("Element at index 0: " + numbers[0]);
System.out.println("Element at index 3: " + numbers[3]);
// Deleting an element from the array
deleteElement(numbers,2);
// Delete element at index 2
System.out.println(
"Array after deleting element at index 2: "
+ Arrays.toString(numbers));
// Searching for an element in the array
int searchElement = 30;
int index = searchElement(numbers, searchElement);
if (index != -1) {
System.out.println("Element " + searchElement
+ " found at index "
+ index);
}
else {
System.out.println("Element " + searchElement
+ " not found in the array");
}
// Sorting the array
Arrays.sort(numbers);
System.out.println("Sorted array: "
+ Arrays.toString(numbers));
}
// Function to delete an element from the array
public static void deleteElement(int[] arr, int index)
{
if (index < 0 || index >= arr.length) {
System.out.println(
"Invalid index. Element cannot be deleted.");
}
else {
for (int i = index; i < arr.length - 1; i++) {
arr[i] = arr[i + 1];
}
arr[arr.length - 1] = 0;
// Set the last element to 0 or default
// value
}
}
// Function to search for an element in the array
public static int searchElement(int[] arr, int element)
{
for (int i = 0; i < arr.length; i++) {
if (arr[i] == element) {
// Element found, return its index
return i;
}
}
// Element not found
return -1;
}}
`
Output
Element at index 0: 10 Element at index 3: 50 Array after deleting element at index 2: [10, 30, 50, 40, 0] Element 30 found at index 1 Sorted array: [0, 10, 30, 40, 50]
Application of One-Dimensional Array
One-Dimensional arrays are widely used in various domains because of its simplicity, efficiency and versatility. Here are the some common applications:
- Lists and Collections
- Data Storage and Retrieval
- Stacks and Queues
- Matrices and Vectors
- Dynamic Programming
- Sorting and Searching Algorithms
- Graph Algorithms
- Histograms and Frequency Counting
- Image Processing
- Cryptography
**Important Notes:
In Java, arrays have a fixed length and this is accessible via the lengthproperty.
For example:
int[] numbers = new int[5];
System.out.println(numbers.length); // Outputs 5
When iterating through an array, always use the **length property to avoid ArrayIndexOutOfBoundsException:
for (int i = 0; i < numbers.length; i++) {
System.out.println(numbers[i]);
}
Arrays are fixed in size, if you need a dynamically resizable collection, consider using classes like ArrayList from the Java Collections Framework.