Postorder Traversal of Binary Tree (original) (raw)

Last Updated : 28 Mar, 2025

**Postorder traversal is a tree traversal method that follows the Left-Right-Root order:

The **left subtree is visited first.
The **right subtree is visited next.
The **root node is processed last.

How does Postorder Traversal work?

**Key Properties:

It is used for tree deletion because subtrees are deleted before the current node.
It is also useful for generating the postfix expression from an expression tree.

Examples:

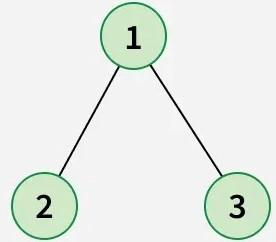
**Input:

**Output: 2 3 1
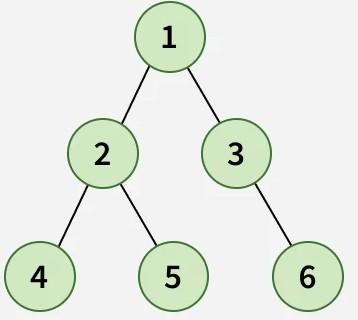
**Explanation: Postorder Traversal visits the nodes in the following order: **Left, **Right, **Root. Therefore, we visit the left node 2, then the right node 3and lastly the root node 1.

**Input:

Output: 4 5 2 6 3 1
Explanation: Postorder Traversal (Left → Right → Root).** Visit 4 → 5 → 2 → 6 → 3 → 1, resulting in 4 5 2 6 3 1.

Algorithm:

If root is NULL then return

Recursively traverse the left subtree.

Recursively traverse the right subtree.

Process the root node (e.g., print its value).

C++ `

#include <bits/stdc++.h> using namespace std;

// Structure of a Binary Tree Node struct Node { int data; struct Node *left, *right; Node(int v) { data = v; left = right = nullptr; } };

// Function to print postorder traversal void printPostorder(struct Node* node) { if (node == nullptr) return;

// First recur on left subtree
printPostorder(node->left);

// Then recur on right subtree
printPostorder(node->right);

// Now deal with the node
cout << node->data << " ";

}

int main() { struct Node* root = new Node(1); root->left = new Node(2); root->right = new Node(3); root->left->left = new Node(4); root->left->right = new Node(5); root->right->right = new Node(6);

printPostorder(root);

return 0;

}

C

#include <stdio.h> #include <stdlib.h>

// Structure of a Binary Tree Node struct Node { int data; struct Node *left, *right; };

// Function to print postorder traversal void printPostorder(struct Node* node) { if (node == NULL) return;

// First recur on left subtree
printPostorder(node->left);

// Then recur on right subtree
printPostorder(node->right);

// Now deal with the node
printf("%d ", node->data);

}

int main() { struct Node* root = (struct Node*)malloc(sizeof(struct Node)); root->data = 1; root->left = (struct Node*)malloc(sizeof(struct Node)); root->left->data = 2; root->right = (struct Node*)malloc(sizeof(struct Node)); root->right->data = 3; root->left->left = (struct Node*)malloc(sizeof(struct Node)); root->left->left->data = 4; root->left->right = (struct Node*)malloc(sizeof(struct Node)); root->left->right->data = 5; root->right->right = (struct Node*)malloc(sizeof(struct Node)); root->right->right->data = 6;

printPostorder(root);

return 0;

}

Java

class Node { int data; Node left, right; Node(int v) { data = v; left = right = null; } }

public class GfG{ // Function to print postorder traversal void printPostorder(Node node) { if (node == null) return;

    // First recur on left subtree
    printPostorder(node.left);

    // Then recur on right subtree
    printPostorder(node.right);

    // Now deal with the node
    System.out.print(node.data + " ");
}

public static void main(String[] args) {
    Node root = new Node(1);
    root.left = new Node(2);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(5);
    root.right.right = new Node(6);

    GfG tree = new GfG();
    tree.printPostorder(root);
}

}

Python

class Node: def init(self, v): self.data = v self.left = None self.right = None

Function to print postorder traversal

def print_postorder(node): if node is None: return

# First recur on left subtree
print_postorder(node.left)

# Then recur on right subtree
print_postorder(node.right)

# Now deal with the node
print(node.data, end=' ')

if name == 'main': root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) root.right.right = Node(6)

print_postorder(root)

C#

using System;

// Structure of a Binary Tree Node public class Node { public int data; public Node left, right; public Node(int v) { data = v; left = right = null; } }

public class GfG {

// Function to print postorder traversal
static void printPostorder(Node node)
{
    if (node == null)
        return;

    // First recur on left subtree
    printPostorder(node.left);

    // Then recur on right subtree
    printPostorder(node.right);

    // Now deal with the node
    Console.Write(node.data + " ");
}

static public void Main()
{

    Node root = new Node(1);
    root.left = new Node(2);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(5);
    root.right.right = new Node(6);

    printPostorder(root);
}

}

JavaScript

// Structure of a Binary Tree Node class Node { constructor(v) { this.data = v; this.left = null; this.right = null; } }

// Function to print postorder traversal function printPostorder(node) { if (node == null) { return; }

// First recur on left subtree printPostorder(node.left);

// Then recur on right subtree printPostorder(node.right);

// Now deal with the node console.log(node.data + " "); }

// Driver code function main() { let root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.right = new Node(6);

printPostorder(root); }

main();

**Time Complexity: O(n)
**Auxiliary Space: O(h), h is the height of the tree

In the worst case, **h can be the same as **n (when the tree is a skewed tree)
In the best case, **h can be the same as **log n (when the tree is a complete tree)