Print negative weight cycle in a Directed Graph (original) (raw)

Last Updated : 22 Aug, 2022

Given a weighted directed graph consisting of V vertices and E edges. The task is to print the cyclic path whose sum of weight is negative. If there is no such path present then print "-1".

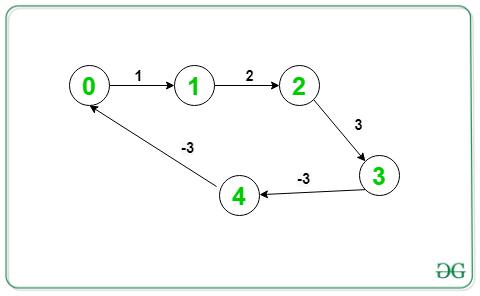
Input: V = 5, E = 5, Below is the graph:

Here, for the given negative cycle o/p (1->2->3->4->1) ; In fig there has to be Edge from 4-->1 not from 4-->0

Output: 1 2 3 4 1
Explanation:
Given graph contains a negative cycle, (1->2->3->4->1)

Input: V = 5, E = 5, Below is the graph:

Output: 0 1 2 3 4 0
Explanation:
Given graph contains a negative cycle, (0->1->2->3->4->0)

Approach: The idea is to use Bellman-Ford Algorithm which is used to detect a negative cycle or not. To print the negative cycles, perform the Nth iteration of Bellman-Ford and pick a vertex from any edge which is relaxed in this iteration. Using this vertex and its ancestors, the negative cycle can be printed. Below are the steps:

• Perform N-1 iterations of Bellman-Ford algorithm and relax each edge (u, v). Keep track of parent of each vertex and store in an array parent[].
• Now, do one more iteration and if no edge relaxation take place in this Nth iteration, then there is no cycle of negative weight exists in the graph.
• Otherwise take a variable C and store the vertex v from any edge (u, v), which is relaxed in the Nth iteration.
• Now, starting from the C vertex go towards its ancestors until a cycle is found and finally print it.
• This cycle will be the desired cycle of negative weight.

Below is the implementation of the above approach:

C++ `

// C++ program for the above approach #include <bits/stdc++.h> using namespace std;

// Structure to represent a weighted // edge in graph struct Edge { int src, dest, weight; };

// Structure to represent a directed // and weighted graph struct Graph {

// V -> Number of vertices,
// E -> Number of edges
int V, E;

// Graph is represented as an
// array of edges
struct Edge* edge;

};

// Creates a new graph with V vertices // and E edges struct Graph* createGraph(int V, int E) { struct Graph* graph = new Graph; graph->V = V; graph->E = E; graph->edge = new Edge[graph->E]; return graph; }

vector vis; // Function runs Bellman-Ford algorithm // and prints negative cycle(if present) void NegCycleBellmanFord(struct Graph* graph, int src) { int V = graph->V; int E = graph->E; int dist[V]; int parent[V];

// Initialize distances from src
// to all other vertices as INFINITE
// and all parent as -1
for (int i = 0; i < V; i++) {

    dist[i] = INT_MAX;
    parent[i] = -1;
}
dist[src] = 0;
vis[src] = 0;
// Relax all edges |V| - 1 times.
bool flg = true;
for (int i = 1; i <= V - 1; i++) {
  if(flg==false)
        break;
  flg=false;
    for (int j = 0; j < E; j++) {

        int u = graph->edge[j].src;
        int v = graph->edge[j].dest;
        int weight = graph->edge[j].weight;

        if (dist[u] != INT_MAX
            && dist[u] + weight < dist[v]) {
            flg = true;
              vis[v] = 1;
            dist[v] = dist[u] + weight;
            parent[v] = u;
        }
    }
}

// Check for negative-weight cycles
int C = -1;
for (int i = 0; i < E; i++) {

    int u = graph->edge[i].src;
    int v = graph->edge[i].dest;
    int weight = graph->edge[i].weight;

    if (dist[u] != INT_MAX
        && dist[u] + weight < dist[v]) {

        // Store one of the vertex of
        // the negative weight cycle
        C = v;
        break;
    }
}

if (C != -1) {

    for (int i = 0; i < V; i++)
        C = parent[C];

    // To store the cycle vertex
    vector<int> cycle;
    for (int v = C;; v = parent[v]) {

        cycle.push_back(v);
        if (v == C
            && cycle.size() > 1)
            break;
    }

    // Reverse cycle[]
    reverse(cycle.begin(), cycle.end());

    // Printing the negative cycle
    for (int v : cycle)
        cout << v << ' ';
    cout << endl;
   return;
}

}

// Driver Code int main() { // Number of vertices in graph int V = 5;

// Number of edges in graph
int E = 5;

struct Graph* graph = createGraph(V, E);
vis.resize(V,0);
// Given Graph
graph->edge[0].src = 1;
graph->edge[0].dest = 0;
graph->edge[0].weight = 1;

graph->edge[1].src = 1;
graph->edge[1].dest = 2;
graph->edge[1].weight = 2;

graph->edge[2].src = 2;
graph->edge[2].dest = 3;
graph->edge[2].weight = 3;

graph->edge[3].src = 3;
graph->edge[3].dest = 4;
graph->edge[3].weight = -3;

graph->edge[4].src = 4;
graph->edge[4].dest = 1;
graph->edge[4].weight = -3;

graph->edge[5].src = 5;
graph->edge[5].dest = 6;
graph->edge[5].weight = -1;

graph->edge[6].src = 6;
graph->edge[6].dest = 7;
graph->edge[6].weight =-1;

graph->edge[7].src = 7;
graph->edge[7].dest = 5;
graph->edge[7].weight =-1;

// Function Call
  for(int src = 0;src<V;src++)
{
  if(vis[src]==0)
     NegCycleBellmanFord(graph, src);
} 
    cout << "-1\n";
return 0;

}

Java

// Java program for the above approach import java.util.ArrayList; import java.util.Collections;

class GFG{

// Structure to represent a weighted // edge in graph static class Edge { int src, dest, weight; }

// Structure to represent a directed // and weighted graph static class Graph {

// V. Number of vertices, E.
// Number of edges
int V, E;

// Graph is represented as
// an array of edges.
Edge[] edge;

}

// Creates a new graph with V vertices // and E edges static Graph createGraph(int V, int E) { Graph graph = new Graph(); graph.V = V; graph.E = E; graph.edge = new Edge[graph.E];

for(int i = 0; i < graph.E; i++)
{
    graph.edge[i] = new Edge();
}

return graph;

}

// Function runs Bellman-Ford algorithm // and prints negative cycle(if present) static void NegCycleBellmanFord(Graph graph, int src) { int V = graph.V; int E = graph.E; int[] dist = new int[V]; int[] parent = new int[V];

// Initialize distances from src
// to all other vertices as INFINITE
// and all parent as -1
for(int i = 0; i < V; i++) 
{
    dist[i] = 1000000;
    parent[i] = -1;
}
dist[src] = 0;

// Relax all edges |V| - 1 times.
for(int i = 1; i <= V - 1; i++)
{
    for(int j = 0; j < E; j++)
    {
        int u = graph.edge[j].src;
        int v = graph.edge[j].dest;
        int weight = graph.edge[j].weight;

        if (dist[u] != 1000000 && 
            dist[u] + weight < dist[v])
        {
            dist[v] = dist[u] + weight;
            parent[v] = u;
        }
    }
}

// Check for negative-weight cycles
int C = -1;
for(int i = 0; i < E; i++) 
{
    int u = graph.edge[i].src;
    int v = graph.edge[i].dest;
    int weight = graph.edge[i].weight;

    if (dist[u] != 1000000 && 
        dist[u] + weight < dist[v])
    {
        
        // Store one of the vertex of
        // the negative weight cycle
        C = v;
        break;
    }
}

if (C != -1)
{
    for(int i = 0; i < V; i++)
        C = parent[C];

    // To store the cycle vertex
    ArrayList<Integer> cycle = new ArrayList<>();
    for(int v = C;; v = parent[v])
    {
        cycle.add(v);
        
        if (v == C && cycle.size() > 1)
            break;
    }

    // Reverse cycle[]
    Collections.reverse(cycle);

    // Printing the negative cycle
    for(int v : cycle)
        System.out.print(v + " ");
        
    System.out.println();
} 
else
    System.out.println(-1);

}

// Driver Code public static void main(String[] args) {

// Number of vertices in graph
int V = 5;

// Number of edges in graph
int E = 5;

Graph graph = createGraph(V, E);

// Given Graph
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
graph.edge[0].weight = 1;

graph.edge[1].src = 1;
graph.edge[1].dest = 2;
graph.edge[1].weight = 2;

graph.edge[2].src = 2;
graph.edge[2].dest = 3;
graph.edge[2].weight = 3;

graph.edge[3].src = 3;
graph.edge[3].dest = 4;
graph.edge[3].weight = -3;

graph.edge[4].src = 4;
graph.edge[4].dest = 1;
graph.edge[4].weight = -3;

// Function Call
NegCycleBellmanFord(graph, 0);

} }

// This code is contributed by sanjeev2552

Python3

Python3 program for the above approach

Structure to represent a weighted

edge in graph

class Edge:
def init(self): self.src = 0 self.dest = 0 self.weight = 0

Structure to represent a directed

and weighted graph

class Graph:

def __init__(self):
    
    # V. Number of vertices, E.
    # Number of edges
    self.V = 0
    self.E = 0
    
    # Graph is represented as
    # an array of edges.
    self.edge = []
 

Creates a new graph with V vertices

and E edges

def createGraph(V, E): graph = Graph(); graph.V = V; graph.E = E; graph.edge = [Edge() for i in range(graph.E)] return graph;

Function runs Bellman-Ford algorithm

and prints negative cycle(if present)

def NegCycleBellmanFord(graph, src): V = graph.V; E = graph.E; dist =[1000000 for i in range(V)] parent =[-1 for i in range(V)] dist[src] = 0;

# Relax all edges |V| - 1 times.
for i in range(1, V):
    for j in range(E):

        u = graph.edge[j].src;
        v = graph.edge[j].dest;
        weight = graph.edge[j].weight;

        if (dist[u] != 1000000 and
            dist[u] + weight < dist[v]):
        
            dist[v] = dist[u] + weight;
            parent[v] = u;

# Check for negative-weight cycles
C = -1;    
for i in range(E):   
    u = graph.edge[i].src;
    v = graph.edge[i].dest;
    weight = graph.edge[i].weight;

    if (dist[u] != 1000000 and 
        dist[u] + weight < dist[v]):
         
        # Store one of the vertex of
        # the negative weight cycle
        C = v;
        break;
     
if (C != -1):       
    for i in range(V):       
        C = parent[C];

    # To store the cycle vertex
    cycle = []       
    v = C
    
    while (True):
        cycle.append(v)
        if (v == C and len(cycle) > 1):
            break;
        v = parent[v]

    # Reverse cycle[]
    cycle.reverse()

    # Printing the negative cycle
    for v in cycle:       
        print(v, end = " ");             
    print()   
else:
    print(-1);

Driver Code

if name=='main':

# Number of vertices in graph
V = 5;

# Number of edges in graph
E = 5; 
graph = createGraph(V, E);

# Given Graph
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
graph.edge[0].weight = 1;

graph.edge[1].src = 1;
graph.edge[1].dest = 2;
graph.edge[1].weight = 2;

graph.edge[2].src = 2;
graph.edge[2].dest = 3;
graph.edge[2].weight = 3;

graph.edge[3].src = 3;
graph.edge[3].dest = 4;
graph.edge[3].weight = -3;

graph.edge[4].src = 4;
graph.edge[4].dest = 1;
graph.edge[4].weight = -3;

# Function Call
NegCycleBellmanFord(graph, 0);

This code is contributed by Pratham76

C#

// C# program for the above approach using System; using System.Collections; using System.Collections.Generic;

class GFG {

// Structure to represent a weighted
// edge in graph
class Edge {
    public int src, dest, weight;
}
// Structure to represent a directed
// and weighted graph
class Graph {

    // V. Number of vertices, E. Number of edges
    public int V, E;

    // graph is represented as an array of edges.
    public Edge[] edge;
}

// Creates a new graph with V vertices
// and E edges
static Graph createGraph(int V, int E)
{
    Graph graph = new Graph();
    graph.V = V;
    graph.E = E;
    graph.edge = new Edge[graph.E];

    for (int i = 0; i < graph.E; i++) {
        graph.edge[i] = new Edge();
    }

    return graph;
}

// Function runs Bellman-Ford algorithm
// and prints negative cycle(if present)
static void NegCycleBellmanFord(Graph graph, int src)
{
    int V = graph.V;
    int E = graph.E;
    int[] dist = new int[V];
    int[] parent = new int[V];

    // Initialize distances from src
    // to all other vertices as INFINITE
    // and all parent as -1
    for (int i = 0; i < V; i++) {

        dist[i] = 1000000;
        parent[i] = -1;
    }
    dist[src] = 0;

    // Relax all edges |V| - 1 times.
    for (int i = 1; i <= V - 1; i++) {
        for (int j = 0; j < E; j++) {

            int u = graph.edge[j].src;
            int v = graph.edge[j].dest;
            int weight = graph.edge[j].weight;

            if (dist[u] != 1000000
                && dist[u] + weight < dist[v]) {

                dist[v] = dist[u] + weight;
                parent[v] = u;
            }
        }
    }

    // Check for negative-weight cycles
    int C = -1;
    for (int i = 0; i < E; i++) {

        int u = graph.edge[i].src;
        int v = graph.edge[i].dest;
        int weight = graph.edge[i].weight;

        if (dist[u] != 1000000
            && dist[u] + weight < dist[v]) {

            // Store one of the vertex of
            // the negative weight cycle
            C = v;
            break;
        }
    }

    if (C != -1) {

        for (int i = 0; i < V; i++)
            C = parent[C];

        // To store the cycle vertex
        ArrayList cycle = new ArrayList();
        for (int v = C;; v = parent[v]) {

            cycle.Add(v);
            if (v == C && cycle.Count > 1)
                break;
        }

        // Reverse cycle[]
        cycle.Reverse();

        // Printing the negative cycle
        foreach(int v in cycle) Console.Write(v + " ");
        Console.WriteLine();
    }
    else
        Console.WriteLine(-1);
}

// Driver Code
public static void Main(string[] args)
{

    // Number of vertices in graph
    int V = 5;

    // Number of edges in graph
    int E = 5;

    Graph graph = createGraph(V, E);

    // Given Graph
    graph.edge[0].src = 0;
    graph.edge[0].dest = 1;
    graph.edge[0].weight = 1;

    graph.edge[1].src = 1;
    graph.edge[1].dest = 2;
    graph.edge[1].weight = 2;

    graph.edge[2].src = 2;
    graph.edge[2].dest = 3;
    graph.edge[2].weight = 3;

    graph.edge[3].src = 3;
    graph.edge[3].dest = 4;
    graph.edge[3].weight = -3;

    graph.edge[4].src = 4;
    graph.edge[4].dest = 1;
    graph.edge[4].weight = -3;

    // Function Call
    NegCycleBellmanFord(graph, 0);
}

}

// This code is contributed by rutvik_56

JavaScript

`

Time Complexity: O(V*E)
Auxiliary Space: O(V)