Python Data Structures (original) (raw)

**Data Structures are a way of organizing data so that it can be accessed more efficiently depending upon the situation. Data Structures are fundamentals of any programming language around which a program is built. Python helps to learn the fundamental of these data structures in a simpler way as compared to other programming languages.

Python Data Structures

In this article, we will discuss the Data Structures in the Python Programming Language and how they are related to some specific Python Data Types. We will discuss all the in-built data structures like list tuples, dictionaries, etc. as well as some advanced data structures like trees, graphs, etc.

Lists

Python Lists are just like the arrays, declared in other languages which is an ordered collection of data. It is very flexible as the items in a list do not need to be of the same type.

The implementation of Python List is similar to Vectors in C++ or ArrayList in JAVA. The costly operation is inserting or deleting the element from the beginning of the List as all the elements are needed to be shifted. Insertion and deletion at the end of the list can also become costly in the case where the preallocated memory becomes full.

We can create a list in python as shown below.

**Example: Creating Python List

Python `

List = [1, 2, 3, "GFG", 2.3] print(List)

Output

[1, 2, 3, 'GFG', 2.3]

List elements can be accessed by the assigned index. In python starting index of the list, sequence is 0 and the ending index is (if N elements are there) N-1.

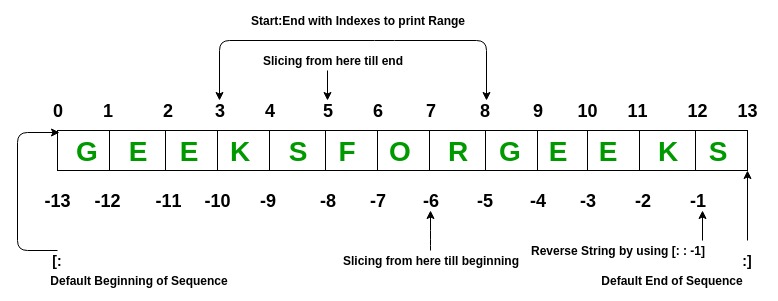
python-list-slicing

**Example: Python List Operations

Python `

Creating a List with

the use of multiple values

List = ["Geeks", "For", "Geeks"] print("\nList containing multiple values: ") print(List)

Creating a Multi-Dimensional List

(By Nesting a list inside a List)

List2 = [['Geeks', 'For'], ['Geeks']] print("\nMulti-Dimensional List: ") print(List2)

accessing a element from the

list using index number

print("Accessing element from the list") print(List[0])
print(List[2])

accessing a element using

negative indexing

print("Accessing element using negative indexing")

print the last element of list

print(List[-1])

print the third last element of list

print(List[-3])

Output

List containing multiple values: ['Geeks', 'For', 'Geeks']

Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks

Dictionary

Python dictionary is like hash tables in any other language with the time complexity of O(1). It is an unordered collection of data values, used to store data values like a map, which, unlike other Data Types that hold only a single value as an element, Dictionary holds the key:value pair. Key-value is provided in the dictionary to make it more optimized.

Indexing of Python Dictionary is done with the help of keys. These are of any hashable type i.e. an object whose can never change like strings, numbers, tuples, etc. We can create a dictionary by using curly braces ({}) or dictionary comprehension.

**Example: Python Dictionary Operations

Python `

Creating a Dictionary

Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]} print("Creating Dictionary: ") print(Dict)

accessing a element using key

print("Accessing a element using key:") print(Dict['Name'])

accessing a element using get()

method

print("Accessing a element using get:") print(Dict.get(1))

creation using Dictionary comprehension

myDict = {x: x**2 for x in [1,2,3,4,5]} print(myDict)

Output

Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25}

Tuple

Python Tuple is a collection of Python objects much like a list but Tuples are immutable in nature i.e. the elements in the tuple cannot be added or removed once created. Just like a List, a Tuple can also contain elements of various types.

In Python, tuples are created by placing a sequence of values separated by ‘comma’ with or without the use of parentheses for grouping of the data sequence.

**Note: Tuples can also be created with a single element, but it is a bit tricky. Having one element in the parentheses is not sufficient, there must be a trailing ‘comma’ to make it a tuple.

Example: Python Tuple Operations

Python `

Creating a Tuple with

the use of Strings

Tuple = ('Geeks', 'For') print("\nTuple with the use of String: ") print(Tuple)

Creating a Tuple with

the use of list

list1 = [1, 2, 4, 5, 6] print("\nTuple using List: ") Tuple = tuple(list1)

Accessing element using indexing

print("First element of tuple") print(Tuple[0])

Accessing element from last

negative indexing

print("\nLast element of tuple") print(Tuple[-1])

print("\nThird last element of tuple") print(Tuple[-3])

Output

Tuple with the use of String: ('Geeks', 'For')

Tuple using List: First element of tuple 1

Last element of tuple 6

Third last element of tuple 4

Set

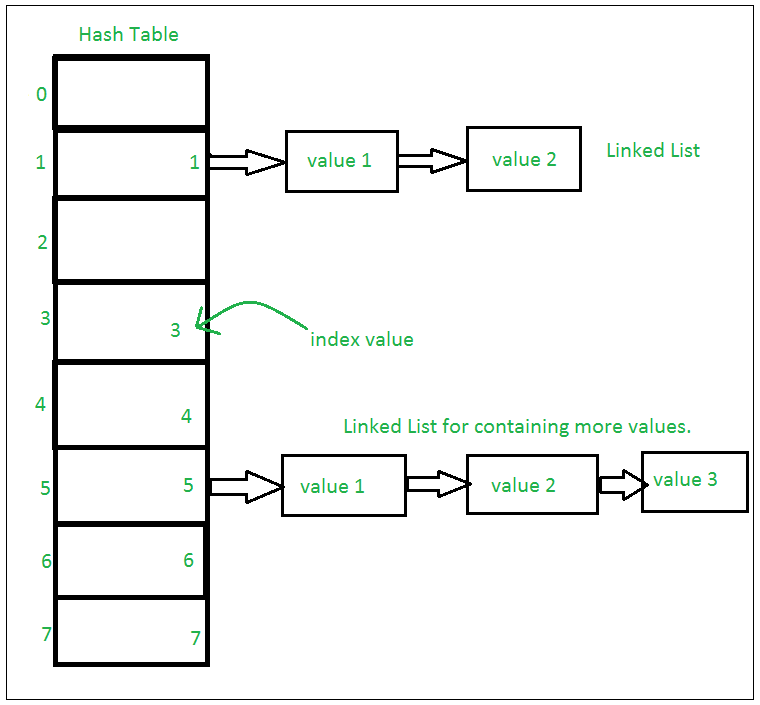
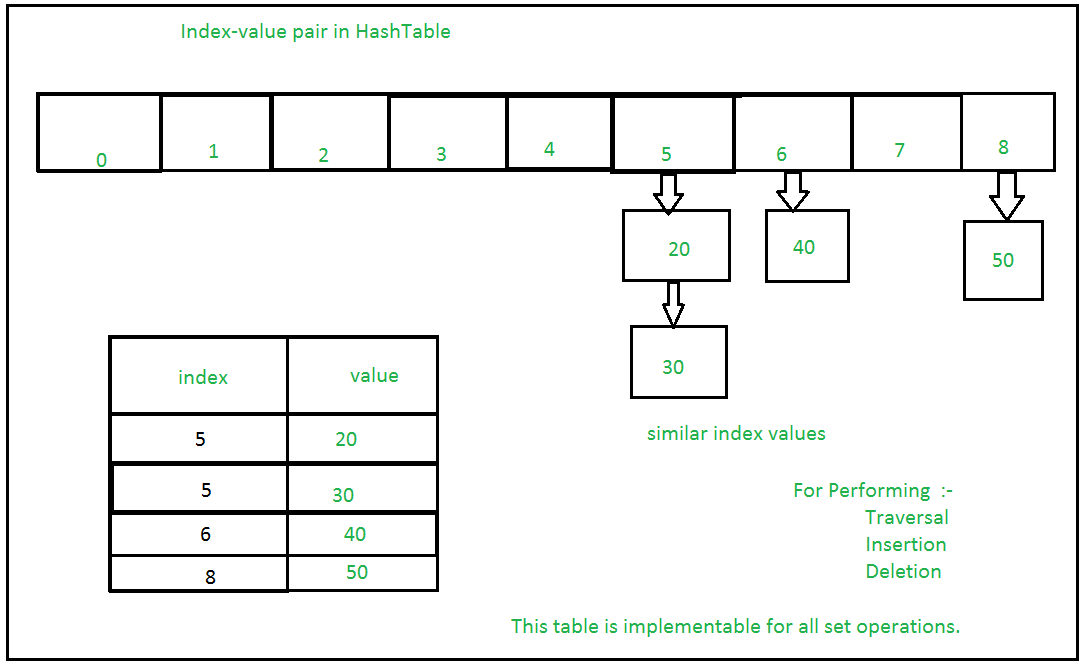
Python Set is an unordered collection of data that is mutable and does not allow any duplicate element. Sets are basically used to include membership testing and eliminating duplicate entries. The data structure used in this is Hashing, a popular technique to perform insertion, deletion, and traversal in O(1) on average.

If Multiple values are present at the same index position, then the value is appended to that index position, to form a Linked List. In, CPython Sets are implemented using a dictionary with dummy variables, where key beings the members set with greater optimizations to the time complexity.

**Set Implementation:

Internal Working of Set

**Sets with Numerous operations on a single HashTable:

Internal Working of Set

Example: Python Set Operations

Python `

Creating a Set with

a mixed type of values

(Having numbers and strings)

Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks']) print("\nSet with the use of Mixed Values") print(Set)

Accessing element using

for loop

print("\nElements of set: ") for i in Set: print(i, end =" ") print()

Checking the element

using in keyword

print("Geeks" in Set)

Output

Set with the use of Mixed Values {1, 2, 'Geeks', 4, 6, 'For'}

Elements of set: 1 2 Geeks 4 6 For True

Frozen Sets

Frozen sets in Python are immutable objects that only support methods and operators that produce a result without affecting the frozen set or sets to which they are applied. While elements of a set can be modified at any time, elements of the frozen set remain the same after creation.

If no parameters are passed, it returns an empty frozenset.

Python `

Same as {"a", "b","c"}

normal_set = set(["a", "b","c"])

print("Normal Set") print(normal_set)

A frozen set

frozen_set = frozenset(["e", "f", "g"])

print("\nFrozen Set") print(frozen_set)

Uncommenting below line would cause error as

we are trying to add element to a frozen set

frozen_set.add("h")

Output

Normal Set {'a', 'c', 'b'}

Frozen Set frozenset({'g', 'e', 'f'})

String

Python Strings are arrays of bytes representing Unicode characters. In simpler terms, a string is an immutable array of characters. Python does not have a character data type, a single character is simply a string with a length of 1.

**Note: As strings are immutable, modifying a string will result in creating a new copy.

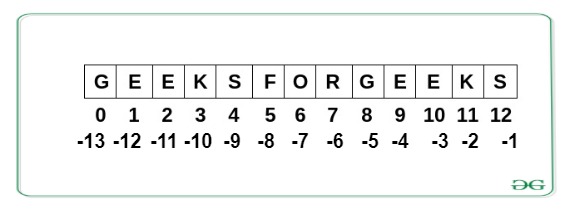
strings

Example: Python Strings Operations

Python `

String = "Welcome to GeeksForGeeks" print("Creating String: ") print(String)

Printing First character

print("\nFirst character of String is: ") print(String[0])

Printing Last character

print("\nLast character of String is: ") print(String[-1])

Output

Creating String: Welcome to GeeksForGeeks

First character of String is: W

Last character of String is: s

Bytearray

Python Bytearray gives a mutable sequence of integers in the range 0 <= x < 256.

Example: Python Bytearray Operations

Python `

Creating bytearray

a = bytearray((12, 8, 25, 2)) print("Creating Bytearray:") print(a)

accessing elements

print("\nAccessing Elements:", a[1])

modifying elements

a[1] = 3 print("\nAfter Modifying:") print(a)

Appending elements

a.append(30) print("\nAfter Adding Elements:") print(a)

Output

Creating Bytearray: bytearray(b'\x0c\x08\x19\x02')

Accessing Elements: 8

After Modifying: bytearray(b'\x0c\x03\x19\x02')

After Adding Elements: bytearray(b'\x0c\x03\x19\x02\x1e')

Till now we have studied all the data structures that come built-in into core Python. Now let dive more deep into Python and see the collections module that provides some containers that are useful in many cases and provide more features than the above-defined functions.

Collections Module

Python collection module was introduced to improve the functionality of the built-in datatypes. It provides various containers let’s see each one of them in detail.

Counters

A counter is a sub-class of the dictionary. It is used to keep the count of the elements in an iterable in the form of an unordered dictionary where the key represents the element in the iterable and value represents the count of that element in the iterable. This is equivalent to a bag or multiset of other languages.

Example: Python Counter Operations

Python `

from collections import Counter

With sequence of items

print(Counter(['B','B','A','B','C','A','B','B','A','C']))

with dictionary

count = Counter({'A':3, 'B':5, 'C':2}) print(count)

count.update(['A', 1]) print(count)

Output

Counter({'B': 5, 'A': 3, 'C': 2}) Counter({'B': 5, 'A': 3, 'C': 2}) Counter({'B': 5, 'A': 4, 'C': 2, 1: 1})

OrderedDict

An OrderedDict is also a sub-class of dictionary but unlike a dictionary, it remembers the order in which the keys were inserted.

Example: Python OrderedDict Operations

Python `

from collections import OrderedDict

print("Before deleting:\n") od = OrderedDict() od['a'] = 1 od['b'] = 2 od['c'] = 3 od['d'] = 4

for key, value in od.items(): print(key, value)

print("\nAfter deleting:\n") od.pop('c') for key, value in od.items(): print(key, value)

print("\nAfter re-inserting:\n") od['c'] = 3 for key, value in od.items(): print(key, value)

Output

Before deleting:

a 1 b 2 c 3 d 4

After deleting:

a 1 b 2 d 4

After re-inserting:

a 1 b 2 d 4 c 3

DefaultDict

DefaultDict is used to provide some default values for the key that does not exist and never raises a KeyError. Its objects can be initialized using DefaultDict() method by passing the data type as an argument.

**Note: default_factory is a function that provides the default value for the dictionary created. If this parameter is absent then the KeyError is raised.

Example: Python DefaultDict Operations

Python `

from collections import defaultdict

Defining the dict

d = defaultdict(int)

L = [1, 2, 3, 4, 2, 4, 1, 2]

Iterate through the list

for keeping the count

for i in L:

# The default value is 0
# so there is no need to
# enter the key first
d[i] += 1

print(d)

Output

defaultdict(<class 'int'>, {1: 2, 2: 3, 3: 1, 4: 2})

ChainMap

A ChainMap encapsulates many dictionaries into a single unit and returns a list of dictionaries. When a key is needed to be found then all the dictionaries are searched one by one until the key is found.

Example: Python ChainMap Operations

Python `

from collections import ChainMap

d1 = {'a': 1, 'b': 2} d2 = {'c': 3, 'd': 4} d3 = {'e': 5, 'f': 6}

Defining the chainmap

c = ChainMap(d1, d2, d3) print(c)

print(c['a']) print(c['g'])

**Output

ChainMap({'a': 1, 'b': 2}, {'c': 3, 'd': 4}, {'e': 5, 'f': 6}) 1

KeyError: 'g'

NamedTuple

A NamedTuple returns a tuple object with names for each position which the ordinary tuples lack. For example, consider a tuple names student where the first element represents fname, second represents lname and the third element represents the DOB. Suppose for calling fname instead of remembering the index position you can actually call the element by using the fname argument, then it will be really easy for accessing tuples element. This functionality is provided by the NamedTuple.

Example: Python NamedTuple Operations

Python `

from collections import namedtuple

Declaring namedtuple()

Student = namedtuple('Student',['name','age','DOB'])

Adding values

S = Student('Nandini','19','2541997')

Access using index

print ("The Student age using index is : ",end ="") print (S[1])

Access using name

print ("The Student name using keyname is : ",end ="") print (S.name)

Output

The Student age using index is : 19 The Student name using keyname is : Nandini

Deque

Deque (Doubly Ended Queue) is the optimized list for quicker append and pop operations from both sides of the container. It provides O(1) time complexity for append and pop operations as compared to the list with O(n) time complexity.

Python Deque is implemented using doubly linked lists therefore the performance for randomly accessing the elements is O(n).

Example: Python Deque Operations

Python `

importing "collections" for deque operations

import collections

initializing deque

de = collections.deque([1,2,3])

using append() to insert element at right end

inserts 4 at the end of deque

de.append(4)

printing modified deque

print("The deque after appending at right is : ") print(de)

using appendleft() to insert element at left end

inserts 6 at the beginning of deque

de.appendleft(6)

printing modified deque

print("The deque after appending at left is : ") print(de)

using pop() to delete element from right end

deletes 4 from the right end of deque

de.pop()

printing modified deque

print("The deque after deleting from right is : ") print(de)

using popleft() to delete element from left end

deletes 6 from the left end of deque

de.popleft()

printing modified deque

print("The deque after deleting from left is : ") print(de)

Output

The deque after appending at right is : deque([1, 2, 3, 4]) The deque after appending at left is : deque([6, 1, 2, 3, 4]) The deque after deleting from right is : deque([6, 1, 2, 3]) The deque after deleting from left is : deque([1, 2, 3])

UserDict

UserDict is a dictionary-like container that acts as a wrapper around the dictionary objects. This container is used when someone wants to create their own dictionary with some modified or new functionality.

Example: Python UserDict

Python `

from collections import UserDict

Creating a Dictionary where

deletion is not allowed

class MyDict(UserDict):

# Function to stop deletion
# from dictionary
def __del__(self):
    raise RuntimeError("Deletion not allowed")
    
# Function to stop pop from
# dictionary
def pop(self, s = None):
    raise RuntimeError("Deletion not allowed")
    
# Function to stop popitem
# from Dictionary
def popitem(self, s = None):
    raise RuntimeError("Deletion not allowed")

Driver's code

d = MyDict({'a':1, 'b': 2, 'c': 3})

print("Original Dictionary") print(d)

d.pop(1)

**Output

Original Dictionary {'a': 1, 'b': 2, 'c': 3}

RuntimeError: Deletion not allowed

UserList

UserList is a list-like container that acts as a wrapper around the list objects. This is useful when someone wants to create their own list with some modified or additional functionality.

Examples: Python UserList

Python `

Python program to demonstrate

userlist

from collections import UserList

Creating a List where

deletion is not allowed

class MyList(UserList):

# Function to stop deletion
# from List
def remove(self, s = None):
    raise RuntimeError("Deletion not allowed")
    
# Function to stop pop from
# List
def pop(self, s = None):
    raise RuntimeError("Deletion not allowed")

Driver's code

L = MyList([1, 2, 3, 4])

print("Original List") print(L)

Inserting to List"

L.append(5) print("After Insertion") print(L)

Deleting From List

L.remove()

**Output

Original List [1, 2, 3, 4] After Insertion [1, 2, 3, 4, 5]

RuntimeError: Deletion not allowed

UserString

UserString is a string-like container and just like UserDict and UserList, it acts as a wrapper around string objects. It is used when someone wants to create their own strings with some modified or additional functionality.

Example: Python UserString

Python `

from collections import UserString

Creating a Mutable String

class Mystring(UserString):

# Function to append to
# string
def append(self, s):
    self.data += s
    
# Function to remove from
# string
def remove(self, s):
    self.data = self.data.replace(s, "")

Driver's code

s1 = Mystring("Geeks") print("Original String:", s1.data)

Appending to string

s1.append("s") print("String After Appending:", s1.data)

Removing from string

s1.remove("e") print("String after Removing:", s1.data)

Output

Original String: Geeks String After Appending: Geekss String after Removing: Gkss

Now after studying all the data structures let’s see some advanced data structures such as stack, queue, graph, linked list, etc. that can be used in Python Language.

Linked List

A linked list is a linear data structure, in which the elements are not stored at contiguous memory locations. The elements in a linked list are linked using pointers as shown in the below image:

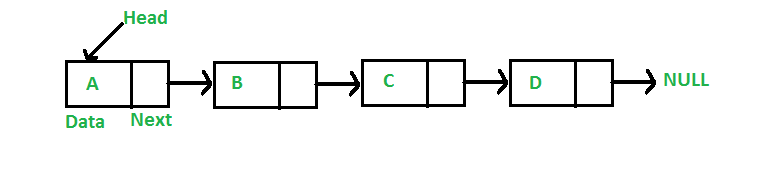
A linked list is represented by a pointer to the first node of the linked list. The first node is called the head. If the linked list is empty, then the value of the head is NULL. Each node in a list consists of at least two parts:

Data
Pointer (Or Reference) to the next node

Example: Defining Linked List in Python

Python `

Node class

class Node:

# Function to initialize the node object
def __init__(self, data):
    self.data = data # Assign data
    self.next = None # Initialize
                    # next as null

Linked List class

class LinkedList:

# Function to initialize the Linked
# List object
def __init__(self):
    self.head = None

Let us create a simple linked list with 3 nodes.

Python `

A simple Python program to introduce a linked list

Node class

class Node:

# Function to initialise the node object
def __init__(self, data):
    self.data = data # Assign data
    self.next = None # Initialize next as null

Linked List class contains a Node object

class LinkedList:

# Function to initialize head
def __init__(self):
    self.head = None

Code execution starts here

if name=='main':

# Start with the empty list
list = LinkedList()

list.head = Node(1)
second = Node(2)
third = Node(3)

'''
Three nodes have been created.
We have references to these three blocks as head,
second and third

list.head     second             third
    |             |                 |
    |             |                 |
+----+------+     +----+------+     +----+------+
| 1 | None |     | 2 | None |     | 3 | None |
+----+------+     +----+------+     +----+------+
'''

list.head.next = second; # Link first node with second

'''
Now next of first Node refers to second. So they
both are linked.

list.head     second             third
    |             |                 |
    |             |                 |
+----+------+     +----+------+     +----+------+
| 1 | o-------->| 2 | null |     | 3 | null |
+----+------+     +----+------+     +----+------+
'''

second.next = third; # Link second node with the third node

'''
Now next of second Node refers to third. So all three
nodes are linked.

list.head     second             third
    |             |                 |
    |             |                 |
+----+------+     +----+------+     +----+------+
| 1 | o-------->| 2 | o-------->| 3 | null |
+----+------+     +----+------+     +----+------+
'''

Linked List Traversal

In the previous program, we have created a simple linked list with three nodes. Let us traverse the created list and print the data of each node. For traversal, let us write a general-purpose function printList() that prints any given list.

Python `

A simple Python program for traversal of a linked list

Node class

class Node:

# Function to initialise the node object
def __init__(self, data):
    self.data = data # Assign data
    self.next = None # Initialize next as null

Linked List class contains a Node object

class LinkedList:

# Function to initialize head
def __init__(self):
    self.head = None

# This function prints contents of linked list
# starting from head
def printList(self):
    temp = self.head
    while (temp):
        print (temp.data)
        temp = temp.next

Code execution starts here

if name=='main':

# Start with the empty list
list = LinkedList()

list.head = Node(1)
second = Node(2)
third = Node(3)

list.head.next = second; # Link first node with second
second.next = third; # Link second node with the third node

list.printList()

Stack

A stack is a linear data structure that stores items in a Last-In/First-Out (LIFO) or First-In/Last-Out (FILO) manner. In stack, a new element is added at one end and an element is removed from that end only. The insert and delete operations are often called push and pop.

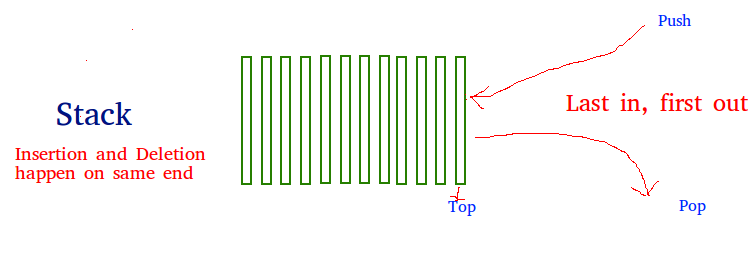
Stack in python

The functions associated with stack are:

**empty() – Returns whether the stack is empty – Time Complexity: O(1)
**size() – Returns the size of the stack – Time Complexity: O(1)
**top() – Returns a reference to the topmost element of the stack – Time Complexity: O(1)
**push(a) – Inserts the element ‘a’ at the top of the stack – Time Complexity: O(1)
**pop() – Deletes the topmost element of the stack – Time Complexity: O(1)

Python Stack Implementation

Stack in Python can be implemented using the following ways:

list
Collections.deque
queue.LifoQueue

**Implementation using List

Python’s built-in data structure list can be used as a stack. Instead of push(), append() is used to add elements to the top of the stack while pop() removes the element in LIFO order.

Python `

stack = []

append() function to push

element in the stack

stack.append('g') stack.append('f') stack.append('g')

print('Initial stack') print(stack)

pop() function to pop

element from stack in

LIFO order

print('\nElements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop())

print('\nStack after elements are popped:') print(stack)

uncommenting print(stack.pop())

will cause an IndexError

as the stack is now empty

Output

Initial stack ['g', 'f', 'g']

Elements popped from stack: g f g

Stack after elements are popped: []

**Implementation using collections.deque:

Python stack can be implemented using the deque class from the collections module. Deque is preferred over the list in the cases where we need quicker append and pop operations from both the ends of the container, as deque provides an O(1) time complexity for append and pop operations as compared to list which provides O(n) time complexity.

Python `

from collections import deque

stack = deque()

append() function to push

element in the stack

stack.append('g') stack.append('f') stack.append('g')

print('Initial stack:') print(stack)

pop() function to pop

element from stack in

LIFO order

print('\nElements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop())

print('\nStack after elements are popped:') print(stack)

uncommenting print(stack.pop())

will cause an IndexError

as the stack is now empty

Output

Initial stack: deque(['g', 'f', 'g'])

Elements popped from stack: g f g

Stack after elements are popped: deque([])

**Implementation using queue module

The queue module also has a LIFO Queue, which is basically a Stack. Data is inserted into Queue using the put() function and get() takes data out from the Queue.

Python `

from queue import LifoQueue

Initializing a stack

stack = LifoQueue(maxsize = 3)

qsize() show the number of elements

in the stack

print(stack.qsize())

put() function to push

element in the stack

stack.put('g') stack.put('f') stack.put('g')

print("Full: ", stack.full()) print("Size: ", stack.qsize())

get() function to pop

element from stack in

LIFO order

print('\nElements popped from the stack') print(stack.get()) print(stack.get()) print(stack.get())

print("\nEmpty: ", stack.empty())

Output

0 Full: True Size: 3

Elements popped from the stack g f g

Empty: True

Queue

As a stack, the queue is a linear data structure that stores items in a First In First Out (FIFO) manner. With a queue, the least recently added item is removed first. A good example of the queue is any queue of consumers for a resource where the consumer that came first is served first.

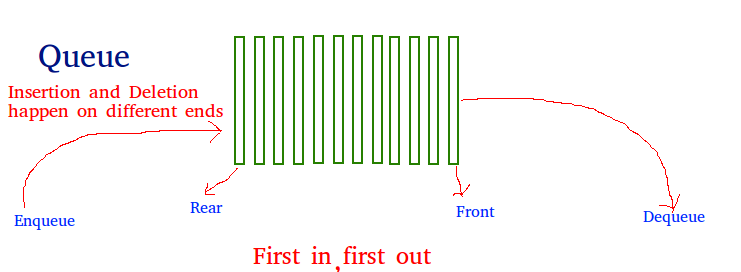
Queue in Python

Operations associated with queue are:

**Enqueue: Adds an item to the queue. If the queue is full, then it is said to be an Overflow condition – Time Complexity: O(1)
**Dequeue: Removes an item from the queue. The items are popped in the same order in which they are pushed. If the queue is empty, then it is said to be an Underflow condition – Time Complexity: O(1)
**Front: Get the front item from queue – Time Complexity: O(1)
**Rear: Get the last item from queue – Time Complexity: O(1)

Python queue Implementation

Queue in Python can be implemented in the following ways:

list
collections.deque
queue.Queue

**Implementation using list

Instead of enqueue() and dequeue(), append() and pop() function is used.

Python `

Initializing a queue

queue = []

Adding elements to the queue

queue.append('g') queue.append('f') queue.append('g')

print("Initial queue") print(queue)

Removing elements from the queue

print("\nElements dequeued from queue") print(queue.pop(0)) print(queue.pop(0)) print(queue.pop(0))

print("\nQueue after removing elements") print(queue)

Uncommenting print(queue.pop(0))

will raise and IndexError

as the queue is now empty

Output

Initial queue ['g', 'f', 'g']

Elements dequeued from queue g f g

Queue after removing elements []

**Implementation using collections.deque

Deque is preferred over the list in the cases where we need quicker append and pop operations from both the ends of the container, as deque provides an O(1) time complexity for append and pop operations as compared to list which provides O(n) time complexity.

Python `

from collections import deque

Initializing a queue

q = deque()

Adding elements to a queue

q.append('g') q.append('f') q.append('g')

print("Initial queue") print(q)

Removing elements from a queue

print("\nElements dequeued from the queue") print(q.popleft()) print(q.popleft()) print(q.popleft())

print("\nQueue after removing elements") print(q)

Uncommenting q.popleft()

will raise an IndexError

as queue is now empty

Output

Initial queue deque(['g', 'f', 'g'])

Elements dequeued from the queue g f g

Queue after removing elements deque([])

**Implementation using the queue.Queue

queue.Queue(maxsize) initializes a variable to a maximum size of maxsize. A maxsize of zero ‘0’ means an infinite queue. This Queue follows the FIFO rule.

Python `

from queue import Queue

Initializing a queue

q = Queue(maxsize = 3)

qsize() give the maxsize

of the Queue

print(q.qsize())

Adding of element to queue

q.put('g') q.put('f') q.put('g')

Return Boolean for Full

Queue

print("\nFull: ", q.full())

Removing element from queue

print("\nElements dequeued from the queue") print(q.get()) print(q.get()) print(q.get())

Return Boolean for Empty

Queue

print("\nEmpty: ", q.empty())

q.put(1) print("\nEmpty: ", q.empty()) print("Full: ", q.full())

This would result into Infinite

Loop as the Queue is empty.

print(q.get())

Output

Full: True

Elements dequeued from the queue g f g

Empty: True

Empty: False Full: False

Priority Queue

Priority Queues are abstract data structures where each data/value in the queue has a certain priority. For example, In airlines, baggage with the title “Business” or “First-class” arrives earlier than the rest. Priority Queue is an extension of the queue with the following properties.

An element with high priority is dequeued before an element with low priority.
If two elements have the same priority, they are served according to their order in the queue. Python `

A simple implementation of Priority Queue

using Queue.

class PriorityQueue(object): def init(self): self.queue = []

def __str__(self):
    return ' '.join([str(i) for i in self.queue])

# for checking if the queue is empty
def isEmpty(self):
    return len(self.queue) == 0

# for inserting an element in the queue
def insert(self, data):
    self.queue.append(data)

# for popping an element based on Priority
def delete(self):
    try:
        max = 0
        for i in range(len(self.queue)):
            if self.queue[i] > self.queue[max]:
                max = i
        item = self.queue[max]
        del self.queue[max]
        return item
    except IndexError:
        print()
        exit()

if name == 'main': myQueue = PriorityQueue() myQueue.insert(12) myQueue.insert(1) myQueue.insert(14) myQueue.insert(7) print(myQueue)
while not myQueue.isEmpty(): print(myQueue.delete())

Output

12 1 14 7 14 12 7 1

Heap queue (or heapq)

heapq module in Python provides the heap data structure that is mainly used to represent a priority queue. The property of this data structure in Python is that each time the smallest heap element is popped(min-heap). Whenever elements are pushed or popped, heap structure is maintained. The heap[0] element also returns the smallest element each time.

It supports the extraction and insertion of the smallest element in the O(log n) times.

Python `

importing "heapq" to implement heap queue

import heapq

initializing list

li = [5, 7, 9, 1, 3]

using heapify to convert list into heap

heapq.heapify(li)

printing created heap

print ("The created heap is : ",end="") print (list(li))

using heappush() to push elements into heap

pushes 4

heapq.heappush(li,4)

printing modified heap

print ("The modified heap after push is : ",end="") print (list(li))

using heappop() to pop smallest element

print ("The popped and smallest element is : ",end="") print (heapq.heappop(li))

Output

The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1

Binary Tree

A tree is a hierarchical data structure that looks like the below figure –

  tree
 ----
  j    <-- root
/   \

f k
/ \
a h z <-- leaves

The topmost node of the tree is called the root whereas the bottommost nodes or the nodes with no children are called the leaf nodes. The nodes that are directly under a node are called its children and the nodes that are directly above something are called its parent.

A binary tree is a tree whose elements can have almost two children. Since each element in a binary tree can have only 2 children, we typically name them the left and right children. A Binary Tree node contains the following parts.

Data
Pointer to left child
Pointer to the right child

Example: Defining Node Class

Python `

A Python class that represents an individual node

in a Binary Tree

class Node: def init(self,key): self.left = None self.right = None self.val = key

Now let’s create a tree with 4 nodes in Python. Let’s assume the tree structure looks like below –

  tree
 ----
  1    <-- root
/   \

2 3
/
4

Example: Adding data to the tree

Python `

Python program to introduce Binary Tree

A class that represents an individual node in a

Binary Tree

class Node: def init(self,key): self.left = None self.right = None self.val = key

create root

root = Node(1) ''' following is the tree after above statement 1 /
None None'''

root.left = Node(2); root.right = Node(3);

''' 2 and 3 become left and right children of 1 1 /
2 3 / \ /
None None None None'''

root.left.left = Node(4); '''4 becomes left child of 2 1 /
2 3 / \ /
4 None None None /
None None'''

Tree Traversal

Trees can be traversed in different ways. Following are the generally used ways for traversing trees. Let us consider the below tree –

  tree
 ----
  1    <-- root
/   \

2 3
/
4 5

**Depth First Traversals:

Inorder (Left, Root, Right) : 4 2 5 1 3
Preorder (Root, Left, Right) : 1 2 4 5 3
Postorder (Left, Right, Root) : 4 5 2 3 1

**Algorithm Inorder(tree)

Traverse the left subtree, i.e., call Inorder(left-subtree)
Visit the root.
Traverse the right subtree, i.e., call Inorder(right-subtree)

**Algorithm Preorder(tree)

Visit the root.
Traverse the left subtree, i.e., call Preorder(left-subtree)
Traverse the right subtree, i.e., call Preorder(right-subtree)

**Algorithm Postorder(tree)

Traverse the left subtree, i.e., call Postorder(left-subtree)
Traverse the right subtree, i.e., call Postorder(right-subtree)
Visit the root. Python `

Python program to for tree traversals

A class that represents an individual node in a

Binary Tree

class Node: def init(self, key): self.left = None self.right = None self.val = key

A function to do inorder tree traversal

def printInorder(root):

if root:

    # First recur on left child
    printInorder(root.left)

    # then print the data of node
    print(root.val),

    # now recur on right child
    printInorder(root.right)

A function to do postorder tree traversal

def printPostorder(root):

if root:

    # First recur on left child
    printPostorder(root.left)

    # the recur on right child
    printPostorder(root.right)

    # now print the data of node
    print(root.val),

A function to do preorder tree traversal

def printPreorder(root):

if root:

    # First print the data of node
    print(root.val),

    # Then recur on left child
    printPreorder(root.left)

    # Finally recur on right child
    printPreorder(root.right)

Driver code

root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print("Preorder traversal of binary tree is") printPreorder(root)

print("\nInorder traversal of binary tree is") printInorder(root)

print("\nPostorder traversal of binary tree is") printPostorder(root)

Output

Preorder traversal of binary tree is 1 2 4 5 3

Inorder traversal of binary tree is 4 2 5 1 3

Postorder traversal of binary tree is 4 5 2 3 1

Time Complexity – O(n)

**Breadth-First or Level Order Traversal

Level order traversal of a tree is breadth-first traversal for the tree. The level order traversal of the above tree is 1 2 3 4 5.

For each node, first, the node is visited and then its child nodes are put in a FIFO queue. Below is the algorithm for the same –

Create an empty queue q
temp_node = root /*start from root*/
Loop while temp_node is not NULL
- print temp_node->data.
- Enqueue temp_node’s children (first left then right children) to q
- Dequeue a node from q Python `

Python program to print level

order traversal using Queue

A node structure

class Node:

# A utility function to create a new node
def __init__(self ,key):
    self.data = key
    self.left = None
    self.right = None

Iterative Method to print the

height of a binary tree

def printLevelOrder(root):

# Base Case
if root is None:
    return

# Create an empty queue
# for level order traversal
queue = []

# Enqueue Root and initialize height
queue.append(root)

while(len(queue) > 0):

    # Print front of queue and
    # remove it from queue
    print (queue[0].data)
    node = queue.pop(0)

    # Enqueue left child
    if node.left is not None:
        queue.append(node.left)

    # Enqueue right child
    if node.right is not None:
        queue.append(node.right)

Driver Program to test above function

root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5)

print ("Level Order Traversal of binary tree is -") printLevelOrder(root)

Output

Level Order Traversal of binary tree is - 1 2 3 4 5

Time Complexity: O(n)

Graph

A graph is a nonlinear data structure consisting of nodes and edges. The nodes are sometimes also referred to as vertices and the edges are lines or arcs that connect any two nodes in the graph. More formally a Graph can be defined as a Graph consisting of a finite set of vertices(or nodes) and a set of edges that connect a pair of nodes.

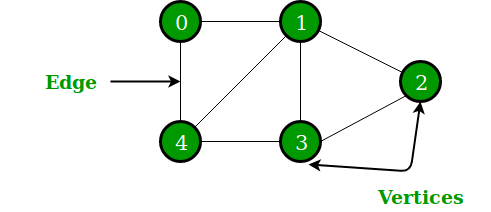
In the above Graph, the set of vertices V = {0,1,2,3,4} and the set of edges E = {01, 12, 23, 34, 04, 14, 13}.

The following two are the most commonly used representations of a graph.

Adjacency Matrix
Adjacency List

Adjacency Matrix

Adjacency Matrix is a 2D array of size V x V where V is the number of vertices in a graph. Let the 2D array be adj[][], a slot adj[i][j] = 1 indicates that there is an edge from vertex i to vertex j. The adjacency matrix for an undirected graph is always symmetric. Adjacency Matrix is also used to represent weighted graphs. If adj[i][j] = w, then there is an edge from vertex i to vertex j with weight w.

Python `

A simple representation of graph using Adjacency Matrix

class Graph: def init(self,numvertex): self.adjMatrix = [[-1]*numvertex for x in range(numvertex)] self.numvertex = numvertex self.vertices = {} self.verticeslist =[0]*numvertex

def set_vertex(self,vtx,id):
    if 0<=vtx<=self.numvertex:
        self.vertices[id] = vtx
        self.verticeslist[vtx] = id

def set_edge(self,frm,to,cost=0):
    frm = self.vertices[frm]
    to = self.vertices[to]
    self.adjMatrix[frm][to] = cost
    
    # for directed graph do not add this
    self.adjMatrix[to][frm] = cost

def get_vertex(self):
    return self.verticeslist

def get_edges(self):
    edges=[]
    for i in range (self.numvertex):
        for j in range (self.numvertex):
            if (self.adjMatrix[i][j]!=-1):
                edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j]))
    return edges
    
def get_matrix(self):
    return self.adjMatrix

G =Graph(6) G.set_vertex(0,'a') G.set_vertex(1,'b') G.set_vertex(2,'c') G.set_vertex(3,'d') G.set_vertex(4,'e') G.set_vertex(5,'f') G.set_edge('a','e',10) G.set_edge('a','c',20) G.set_edge('c','b',30) G.set_edge('b','e',40) G.set_edge('e','d',50) G.set_edge('f','e',60)

print("Vertices of Graph") print(G.get_vertex())

print("Edges of Graph") print(G.get_edges())

print("Adjacency Matrix of Graph") print(G.get_matrix())

**Output

Vertices of Graph

[‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’]

Edges of Graph

[(‘a’, ‘c’, 20), (‘a’, ‘e’, 10), (‘b’, ‘c’, 30), (‘b’, ‘e’, 40), (‘c’, ‘a’, 20), (‘c’, ‘b’, 30), (‘d’, ‘e’, 50), (‘e’, ‘a’, 10), (‘e’, ‘b’, 40), (‘e’, ‘d’, 50), (‘e’, ‘f’, 60), (‘f’, ‘e’, 60)]

Adjacency Matrix of Graph

[[-1, -1, 20, -1, 10, -1], [-1, -1, 30, -1, 40, -1], [20, 30, -1, -1, -1, -1], [-1, -1, -1, -1, 50, -1], [10, 40, -1, 50, -1, 60], [-1, -1, -1, -1, 60, -1]]

Adjacency List

An array of lists is used. The size of the array is equal to the number of vertices. Let the array be an array[]. An entry array[i] represents the list of vertices adjacent to the ith vertex. This representation can also be used to represent a weighted graph. The weights of edges can be represented as lists of pairs. Following is the adjacency list representation of the above graph.

Adjacency List Representation of Graph

Python `

A class to represent the adjacency list of the node

class AdjNode: def init(self, data): self.vertex = data self.next = None

A class to represent a graph. A graph

is the list of the adjacency lists.

Size of the array will be the no. of the

vertices "V"

class Graph: def init(self, vertices): self.V = vertices self.graph = [None] * self.V

# Function to add an edge in an undirected graph
def add_edge(self, src, dest):
  
    # Adding the node to the source node
    node = AdjNode(dest)
    node.next = self.graph[src]
    self.graph[src] = node

    # Adding the source node to the destination as
    # it is the undirected graph
    node = AdjNode(src)
    node.next = self.graph[dest]
    self.graph[dest] = node

# Function to print the graph
def print_graph(self):
    for i in range(self.V):
        print("Adjacency list of vertex {}\n head".format(i), end="")
        temp = self.graph[i]
        while temp:
            print(" -> {}".format(temp.vertex), end="")
            temp = temp.next
        print(" \n")

Driver program to the above graph class

if name == "main": V = 5 graph = Graph(V) graph.add_edge(0, 1) graph.add_edge(0, 4) graph.add_edge(1, 2) graph.add_edge(1, 3) graph.add_edge(1, 4) graph.add_edge(2, 3) graph.add_edge(3, 4)

graph.print_graph()

Output

Adjacency list of vertex 0 head -> 4 -> 1

Adjacency list of vertex 1 head -> 4 -> 3 -> 2 -> 0

Adjacency list of vertex 2 head -> 3 -> 1

Adjacency list of vertex 3 head -> 4 -> 2 -> 1

Adjacency list of vertex 4 head -> 3 -> 1 -> 0

Graph Traversal

**Breadth-First Search or BFS

Breadth-First Traversal for a graph is similar to Breadth-First Traversal of a tree. The only catch here is, unlike trees, graphs may contain cycles, so we may come to the same node again. To avoid processing a node more than once, we use a boolean visited array. For simplicity, it is assumed that all vertices are reachable from the starting vertex.

For example, in the following graph, we start traversal from vertex 2. When we come to vertex 0, we look for all adjacent vertices of it. 2 is also an adjacent vertex of 0. If we don’t mark visited vertices, then 2 will be processed again and it will become a non-terminating process. A Breadth-First Traversal of the following graph is 2, 0, 3, 1.

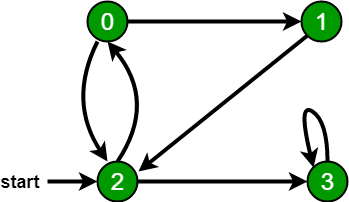
Python `

Python3 Program to print BFS traversal

from a given source vertex. BFS(int s)

traverses vertices reachable from s.

from collections import defaultdict

This class represents a directed graph

using adjacency list representation

class Graph:

# Constructor
def __init__(self):

    # default dictionary to store graph
    self.graph = defaultdict(list)

# function to add an edge to graph
def addEdge(self,u,v):
    self.graph[u].append(v)

# Function to print a BFS of graph
def BFS(self, s):

    # Mark all the vertices as not visited
    visited = [False] * (max(self.graph) + 1)

    # Create a queue for BFS
    queue = []

    # Mark the source node as
    # visited and enqueue it
    queue.append(s)
    visited[s] = True

    while queue:

        # Dequeue a vertex from
        # queue and print it
        s = queue.pop(0)
        print (s, end = " ")

        # Get all adjacent vertices of the
        # dequeued vertex s. If a adjacent
        # has not been visited, then mark it
        # visited and enqueue it
        for i in self.graph[s]:
            if visited[i] == False:
                queue.append(i)
                visited[i] = True

Driver code

Create a graph given in

the above diagram

g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3)

print ("Following is Breadth First Traversal" " (starting from vertex 2)") g.BFS(2)

This code is contributed by Neelam Yadav

Output

Following is Breadth First Traversal (starting from vertex 2) 2 0 3 1

Time Complexity: O(V+E) where V is the number of vertices in the graph and E is the number of edges in the graph.

**Depth First Search or DFS

Depth First Traversal for a graph is similar to Depth First Traversal of a tree. The only catch here is, unlike trees, graphs may contain cycles, a node may be visited twice. To avoid processing a node more than once, use a boolean visited array.

**Algorithm:

Create a recursive function that takes the index of the node and a visited array.
Mark the current node as visited and print the node.
Traverse all the adjacent and unmarked nodes and call the recursive function with the index of the adjacent node. Python `

Python3 program to print DFS traversal

from a given graph

from collections import defaultdict

This class represents a directed graph using

adjacency list representation

class Graph:

# Constructor
def __init__(self):

    # default dictionary to store graph
    self.graph = defaultdict(list)

# function to add an edge to graph
def addEdge(self, u, v):
    self.graph[u].append(v)

# A function used by DFS
def DFSUtil(self, v, visited):

    # Mark the current node as visited
    # and print it
    visited.add(v)
    print(v, end=' ')

    # Recur for all the vertices
    # adjacent to this vertex
    for neighbour in self.graph[v]:
        if neighbour not in visited:
            self.DFSUtil(neighbour, visited)

# The function to do DFS traversal. It uses
# recursive DFSUtil()
def DFS(self, v):

    # Create a set to store visited vertices
    visited = set()

    # Call the recursive helper function
    # to print DFS traversal
    self.DFSUtil(v, visited)

Driver code

Create a graph given

in the above diagram

g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3)

print("Following is DFS from (starting from vertex 2)") g.DFS(2)

Output

Following is DFS from (starting from vertex 2) 2 0 1 3

Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.