Queue using Stacks (original) (raw)

Last Updated : 28 Mar, 2025

Given a stack that supports push and pop operations, your task is to implement a queue using one or more instances of that stack along with its operations.

Stack and Queue with insert and delete operations

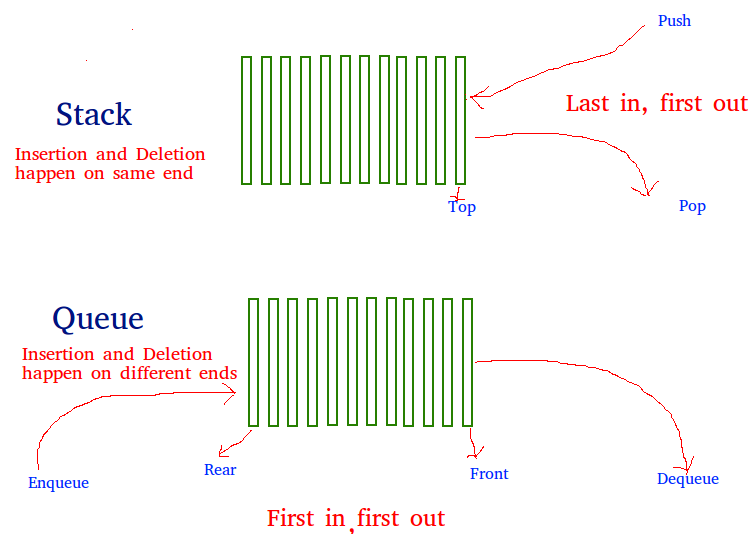
Table of Content

By Making Enqueue Operation Costly
By Making Dequeue Operation Costly
Queue Implementation Using One Stack and Recursion

**By Making Enqueue Operation Costly

A queue can be implemented using two stacks. Let the queue be represented as q, and the stacks used for its implementation be s1 and s2.

In this approach, the **enqueue operation is made costly by transferring elements from stack1 to stack2 before adding the new element. This ensures that the elements in stack2 are in the correct order for dequeuing. The **dequeue operation remains efficient, as it simply involves popping elements from stack2.

**enqueue(q, x):

While stack1 is not empty, push everything from stack1 to stack2.
Push x to stack1 (assuming size of stacks is unlimited).
Push everything back to stack1.

**dequeue(q):

If stack1 is empty then error.
Pop an item from stack1 and return it.

Below is given the **implementation:

C++ `

#include <bits/stdc++.h> using namespace std;

struct Queue { stack s1, s2;

void enqueue(int x) {

    // Move all elements from s1 to s2
    while (!s1.empty()) {
        s2.push(s1.top());
        s1.pop();
    }

    // Push item into s1
    s1.push(x);

    // Push everything back to s1
    while (!s2.empty()) {
        s1.push(s2.top());
        s2.pop();
    }
}

// Dequeue an item from the queue
int dequeue() {

    // if first stack is empty
    if (s1.empty()) {
        return -1;
    }

    // Return top of s1
    int x = s1.top();
    s1.pop();
    return x;
}

};

// Driver code int main() { Queue q; q.enqueue(1); q.enqueue(2); q.enqueue(3);

cout << q.dequeue() << '\n';
cout << q.dequeue() << '\n';
cout << q.dequeue() << '\n';

return 0;

}

Java

import java.util.*;

public class GfG {

static class Queue {
    Stack<Integer> s1 = new Stack<>();
    Stack<Integer> s2 = new Stack<>();

    void enqueue(int x) {

        // Move all elements from s1 to s2
        while (!s1.empty()) {
            s2.push(s1.peek());
            s1.pop();
        }

        // Push item into s1
        s1.push(x);

        // Push everything back to s1
        while (!s2.empty()) {
            s1.push(s2.peek());
            s2.pop();
        }
    }

    // Dequeue an item from the queue
    int dequeue() {

        // if first stack is empty
        if (s1.empty()) {
            return -1;
        }

        // Return top of s1
        int x = s1.peek();
        s1.pop();
        return x;
    }
}

public static void main(String[] args) {
    Queue q = new Queue();
    q.enqueue(1);
    q.enqueue(2);
    q.enqueue(3);

    System.out.println(q.dequeue());
    System.out.println(q.dequeue());
    System.out.println(q.dequeue());
}

}

Python

class Queue: def init(self): self.s1 = [] self.s2 = []

def enqueue(self, x):

    # Move all elements from s1 to s2
    while self.s1:
        self.s2.append(self.s1.pop())

    # Push item into s1
    self.s1.append(x)

    # Push everything back to s1
    while self.s2:
        self.s1.append(self.s2.pop())

# Dequeue an item from the queue
def dequeue(self):

    # if first stack is empty
    if not self.s1:
        return -1

    # Return top of s1
    x = self.s1.pop()
    return x

if name == "main": q = Queue() q.enqueue(1) q.enqueue(2) q.enqueue(3)

print(q.dequeue())
print(q.dequeue())
print(q.dequeue())

C#

using System; using System.Collections.Generic;

public class GfG {

public class Queue {
    Stack<int> s1 = new Stack<int>();
    Stack<int> s2 = new Stack<int>();

    public void Enqueue(int x) {

        // Move all elements from s1 to s2
        while (s1.Count > 0) {
            s2.Push(s1.Peek());
            s1.Pop();
        }

        // Push item into s1
        s1.Push(x);

        // Push everything back to s1
        while (s2.Count > 0) {
            s1.Push(s2.Peek());
            s2.Pop();
        }
    }

    // Dequeue an item from the queue
    public int Dequeue() {

        // if first stack is empty
        if (s1.Count == 0) {
            return -1;
        }

        // Return top of s1
        int x = s1.Peek();
        s1.Pop();
        return x;
    }
}

public static void Main(string[] args) {
    Queue q = new Queue();
    q.Enqueue(1);
    q.Enqueue(2);
    q.Enqueue(3);

    Console.WriteLine(q.Dequeue());
    Console.WriteLine(q.Dequeue());
    Console.WriteLine(q.Dequeue());
}

}

JavaScript

// class Queue { constructor() { this.s1 = []; this.s2 = []; }

enqueue(x) {

    // Move all elements from s1 to s2
    while (this.s1.length) {
        this.s2.push(this.s1.pop());
    }

    // Push item into s1
    this.s1.push(x);

    // Push everything back to s1
    while (this.s2.length) {
        this.s1.push(this.s2.pop());
    }
}

// Dequeue an item from the queue
dequeue() {

    // if first stack is empty
    if (this.s1.length === 0) {
        return -1;
    }

    // Return top of s1
    let x = this.s1.pop();
    return x;
}

}

function main() { let q = new Queue(); q.enqueue(1); q.enqueue(2); q.enqueue(3);

console.log(q.dequeue());
console.log(q.dequeue());
console.log(q.dequeue());

}

main();

**Time Complexity: O(n), for push operation, and O(1) for pop operation.
**Auxiliary Space: O(n).

**By Making Dequeue Operation Costly

In this approach, the new element is pushed onto the top of stack1 during the **enqueue operation. For the **dequeue operation, if stack2 is empty, all elements are transferred from stack1 to stack2, and the element at the top of stack2 is returned.

**enqueue(q, x):

Push x to stack1 (assuming size of stacks is unlimited).

**dequeue(q):

If both stacks are empty then error.
If stack2 is empty
- While stack1 is not empty, push everything from stack1 to stack2.
Pop the element from stack2 and return it.

Below is given the **implementation:

C++ `

#include <bits/stdc++.h> using namespace std;

struct Queue { stack s1, s2;

// Enqueue an item to the queue
void enqueue(int x) {

    // Push item into the first stack
    s1.push(x);
}

// Dequeue an item from the queue
int dequeue() {

    // if both stacks are empty
    if (s1.empty() && s2.empty()) {
        return -1;
    }

    // if s2 is empty, move
    // elements from s1
    if (s2.empty()) {
        while (!s1.empty()) {
            s2.push(s1.top());
            s1.pop();
        }
    }

    // return the top item from s2
    int x = s2.top();
    s2.pop();
    return x;
}

};

int main() { Queue q;

q.enqueue(1);
q.enqueue(2);
q.enqueue(3);

cout << q.dequeue() << '\n'; 
cout << q.dequeue() << '\n'; 
cout << q.dequeue() << '\n'; 

return 0;

}

Java

import java.util.*;

public class GfG {

static class Queue {
    Stack<Integer> s1 = new Stack<>();
    Stack<Integer> s2 = new Stack<>();

    // Enqueue an item to the queue
    void enqueue(int x) {

        // Push item into the first stack
        s1.push(x);
    }

    // Dequeue an item from the queue
    int dequeue() {

        // if both stacks are empty
        if (s1.empty() && s2.empty()) {
            return -1;
        }

        // if s2 is empty, move
        // elements from s1
        if (s2.empty()) {
            while (!s1.empty()) {
                s2.push(s1.peek());
                s1.pop();
            }
        }

        // return the top item from s2
        int x = s2.peek();
        s2.pop();
        return x;
    }
}

public static void main(String[] args) {
    Queue q = new Queue();

    q.enqueue(1);
    q.enqueue(2);
    q.enqueue(3);

    System.out.println(q.dequeue());
    System.out.println(q.dequeue());
    System.out.println(q.dequeue());
}

}

Python

class Queue: def init(self): self.s1 = [] self.s2 = []

# Enqueue an item to the queue
def enqueue(self, x):

    # Push item into the first stack
    self.s1.append(x)

# Dequeue an item from the queue
def dequeue(self):

    # if both stacks are empty
    if not self.s1 and not self.s2:
        return -1

    # if s2 is empty, move
    # elements from s1
    if not self.s2:
        while self.s1:
            self.s2.append(self.s1.pop())

    # return the top item from s2
    x = self.s2.pop()
    return x

if name == "main": q = Queue()

q.enqueue(1)
q.enqueue(2)
q.enqueue(3)

print(q.dequeue())
print(q.dequeue())
print(q.dequeue())

C#

using System; using System.Collections.Generic;

public class GfG {

public class Queue {
    Stack<int> s1 = new Stack<int>();
    Stack<int> s2 = new Stack<int>();

    // Enqueue an item to the queue
    public void Enqueue(int x) {

        // Push item into the first stack
        s1.Push(x);
    }

    // Dequeue an item from the queue
    public int Dequeue() {

        // if both stacks are empty
        if (s1.Count == 0 && s2.Count == 0) {
            return -1;
        }

        // if s2 is empty, move
        // elements from s1
        if (s2.Count == 0) {
            while (s1.Count > 0) {
                s2.Push(s1.Peek());
                s1.Pop();
            }
        }

        // return the top item from s2
        int x = s2.Peek();
        s2.Pop();
        return x;
    }
}

public static void Main(string[] args) {
    Queue q = new Queue();

    q.Enqueue(1);
    q.Enqueue(2);
    q.Enqueue(3);

    Console.WriteLine(q.Dequeue());
    Console.WriteLine(q.Dequeue());
    Console.WriteLine(q.Dequeue());
}

}

JavaScript

// class Queue { constructor() { this.s1 = []; this.s2 = []; }

// Enqueue an item to the queue
enqueue(x) {

    // Push item into the first stack
    this.s1.push(x);
}

// Dequeue an item from the queue
dequeue() {

    // if both stacks are empty
    if (this.s1.length === 0 && this.s2.length === 0) {
        return -1;
    }

    // if s2 is empty, move
    // elements from s1
    if (this.s2.length === 0) {
        while (this.s1.length) {
            this.s2.push(this.s1.pop());
        }
    }

    // return the top item from s2
    let x = this.s2.pop();
    return x;
}

}

function main() { let q = new Queue();

q.enqueue(1);
q.enqueue(2);
q.enqueue(3);

console.log(q.dequeue());
console.log(q.dequeue());
console.log(q.dequeue());

}

main();

**Time Complexity: O(n), for pop operation, and O(1) for push operation. This approach is definitely more efficient than first approach. In the first approach, all elements are moved twice during the **enqueue operation, which is less efficient. However, in this approach, elements are only moved once during the **dequeue operation, and only if stack2 is empty. This leads to an amortized time complexity of the **dequeue operation being Θ(1).
**Space Complexity: O(n)

Queue Implementation Using One Stack and Recursion

A queue can also be implemented using a single user-defined stack and recursion (via the function call stack).

**enqueue(x)

Push the element x onto stack1.

**dequeue()

If stack1 is empty, return an error.
If stack1 has only one element, return it.
Otherwise, recursively pop all elements from stack1, store the popped element in a variable res, then push res back into stack1 and return res.

Step 3 ensures that the last popped element is always returned. Since the recursion halts when there is only one item left in stack1 (as described in step 2), the last element of stack1 is returned by the dequeue() function, with all other elements being pushed back into stack1 in the process.

Below is given the **implementation:

C++ `

#include <bits/stdc++.h> using namespace std;

struct Queue { stack s;

// Enqueue an item to the queue
void enqueue(int x) {
    s.push(x);
}

// Dequeue an item from the queue
int dequeue() {
    if (s.empty()) {
        return -1;
    }

    // pop an item from the stack
    int x = s.top();
    s.pop();

    // if stack becomes empty, return
    // the popped item
    if (s.empty())
        return x;

    // recursive call
    int item = dequeue();

    // push popped item back to the stack
    s.push(x);

    // return the result of dequeue() call
    return item;
}

};

int main() { Queue q; q.enqueue(1); q.enqueue(2); q.enqueue(3);

cout << q.dequeue() << '\n';
cout << q.dequeue() << '\n';
cout << q.dequeue() << '\n';

return 0;

}

Java

import java.util.*;

public class GfG {

static class Queue {
    Stack<Integer> s = new Stack<>();

    // Enqueue an item to the queue
    void enqueue(int x) {
        s.push(x);
    }

    // Dequeue an item from the queue
    int dequeue() {
        if (s.empty()) {
            return -1;
        }

        // pop an item from the stack
        int x = s.peek();
        s.pop();

        // if stack becomes empty, return
        // the popped item
        if (s.empty())
            return x;

        // recursive call
        int item = dequeue();

        // push popped item back to the stack
        s.push(x);

        // return the result of dequeue() call
        return item;
    }
}

public static void main(String[] args) {
    Queue q = new Queue();
    q.enqueue(1);
    q.enqueue(2);
    q.enqueue(3);

    System.out.println(q.dequeue());
    System.out.println(q.dequeue());
    System.out.println(q.dequeue());
}

}

Python

class Queue: def init(self): self.s = []

# Enqueue an item to the queue
def enqueue(self, x):
    self.s.append(x)

# Dequeue an item from the queue
def dequeue(self):
    if not self.s:
        return -1

    # pop an item from the stack
    x = self.s[-1]
    self.s.pop()

    # if stack becomes empty, return
    # the popped item
    if not self.s:
        return x

    # recursive call
    item = self.dequeue()

    # push popped item back to the stack
    self.s.append(x)

    # return the result of dequeue() call
    return item

if name == "main": q = Queue() q.enqueue(1) q.enqueue(2) q.enqueue(3)

print(q.dequeue())
print(q.dequeue())
print(q.dequeue())

C#

using System; using System.Collections.Generic;

public class GfG {

public class Queue {
    Stack<int> s = new Stack<int>();

    // Enqueue an item to the queue
    public void Enqueue(int x) {
        s.Push(x);
    }

    // Dequeue an item from the queue
    public int Dequeue() {
        if (s.Count == 0) {
            return -1;
        }

        // pop an item from the stack
        int x = s.Peek();
        s.Pop();

        // if stack becomes empty, return
        // the popped item
        if (s.Count == 0)
            return x;

        // recursive call
        int item = Dequeue();

        // push popped item back to the stack
        s.Push(x);

        // return the result of dequeue() call
        return item;
    }
}

public static void Main(string[] args) {
    Queue q = new Queue();
    q.Enqueue(1);
    q.Enqueue(2);
    q.Enqueue(3);

    Console.WriteLine(q.Dequeue());
    Console.WriteLine(q.Dequeue());
    Console.WriteLine(q.Dequeue());
}

}

JavaScript

// class Queue { constructor() { this.s = []; }

// Enqueue an item to the queue
enqueue(x) {
    this.s.push(x);
}

// Dequeue an item from the queue
dequeue() {
    if (this.s.length === 0) {
        return -1;
    }

    // pop an item from the stack
    let x = this.s[this.s.length - 1];
    this.s.pop();

    // if stack becomes empty, return
    // the popped item
    if (this.s.length === 0)
        return x;

    // recursive call
    let item = this.dequeue();

    // push popped item back to the stack
    this.s.push(x);

    // return the result of dequeue() call
    return item;
}

}

function main() { let q = new Queue(); q.enqueue(1); q.enqueue(2); q.enqueue(3);

console.log(q.dequeue());
console.log(q.dequeue());
console.log(q.dequeue());

}

main();

**Time Complexity: O(n), for push operation, and O(1) for pop operation. The difference from above method is that in this method element is returned and all elements are restored back in a single call.
**Auxiliary Space: O(n)