Sort an array after applying the given equation (original) (raw)

Last Updated : 16 May, 2025

Try it on GfG Practice

Given an integer array **arr[] sorted in ascending order, along with three integers: **A, B, and C. The task is to transform each element **x in the array using the quadratic function **A*(x^2) + B*x + C. After applying this transformation to every element, return the modified array in sorted order.

**Examples:

**Input: arr[] = [-4, -2, 0, 2, 4], A = 1, B = 3, C = 5
**Output: [3, 5, 9, 15, 33]
**Explanation: After applying f(x) = 1*x2+ 3*x + 5 to each x, we get [9, 3, 5, 15, 33]. After sorting this array, the array becomes [3, 5, 9, 15, 33].

**Input: arr[] = [-3, -1, 2, 4], A = -1, B = 0, C = 0
**Output: [-16, -9, -4, -1]
**Explanation: After applying f(x) = -1*x2 to each x, we get [-9, -1, -4, -16 ]. After sorting this array, the array becomes [-16, -9, -4, -1].

**Input: arr[] = [-1, 0, 1, 2, 3, 4], A = -1, B = 2, C = -1
**Output: [-9, -4, -4, -1, -1, 0]

Table of Content

• [Brute Force Approach] Apply the Equation and Sort - O(n*log(n)) Time and O(1) Space
• [Expected Approach] Using Two Pointers - O(n) Time and O(n) Space

[Brute Force Approach] Apply the Equation and Sort - O(n*log(n)) Time and O(1) Space

The **idea is to directly transform each element in the array, i.e. for each element **x in **arr[], apply the given equation **A*x 2 + B*x + C in-place and then simply **sort the array in **ascending order.

C++ `

#include <bits/stdc++.h> using namespace std;

// Function to apply quadratic transformation int evaluate(int x, int A, int B, int C) { return A * x * x + B * x + C; }

// Function to transform and sort the array in-place vector sortArray(vector &arr, int A, int B, int C) { int n = arr.size();

vector<int> transformed;
// Apply the transformation
for (int i = 0; i < n; i++) {
    transformed.push_back(evaluate(arr[i], A, B, C));
}

// Sort the transformed array
sort(transformed.begin(), transformed.end());

return transformed;

}

int main() { vector arr = {-4, -2, 0, 2, 4}; int A = 1, B = 3, C = 5;

vector<int> res = sortArray(arr, A, B, C);

for (int val : res) {
    cout << val << " ";
}

return 0;

}

Java

import java.util.*;

class GfG {

// Function to apply quadratic transformation
static int evaluate(int x, int A, int B, int C) {
    return A * x * x + B * x + C;
}

// Function to transform and sort the array (returns ArrayList<Integer>)
static ArrayList<Integer> sortArray(int[] arr, int A, int B, int C) {
    int n = arr.length;
    Integer[] transformed = new Integer[n];

    // Apply the transformation and store in array
    for (int i = 0; i < n; i++) {
        transformed[i] = evaluate(arr[i], A, B, C);
    }

    // Sort the array
    Arrays.sort(transformed);

    // Convert to ArrayList and return
    return new ArrayList<>(Arrays.asList(transformed));
}

public static void main(String[] args) {
    int[] arr = {-4, -2, 0, 2, 4};
    int A = 1, B = 3, C = 5;

    ArrayList<Integer> res = sortArray(arr, A, B, C);

    for (int val : res) {
        System.out.print(val + " ");
    }
}

}

Python

Python Code to Sort array after applying

equation using Brute Force Approach

Function to apply quadratic transformation

def evaluate(x, A, B, C): return A * x * x + B * x + C

Function to transform and sort the array, returning a new list

def sortArray(arr, A, B, C): # Create a new array with the transformed values transformed = [evaluate(x, A, B, C) for x in arr]

# Sort the transformed array
transformed.sort()

return transformed

if name == "main": arr = [-4, -2, 0, 2, 4] A, B, C = 1, 3, 5

res = sortArray(arr, A, B, C)

for val in res:
    print(val, end=" ")

C#

using System; using System.Collections.Generic;

class GfG{ // Function to apply quadratic transformation static int evaluate(int x, int A, int B, int C){

    return A * x * x + B * x + C;
}

// Function to transform and sort the array (returns List<int>)
static List<int> sortArray(int[] arr, int A, int B, int C){
    
    int n = arr.Length;
    int[] transformed = new int[n];

    // Apply transformation
    for (int i = 0; i < n; i++){
        
        transformed[i] = evaluate(arr[i], A, B, C);
    }

    // Sort the transformed array
    Array.Sort(transformed);

    // Convert to List<int> and return
    return new List<int>(transformed);
}

static void Main(){
    
    int[] arr = { -4, -2, 0, 2, 4 };
    int A = 1, B = 3, C = 5;

    List<int> res = sortArray(arr, A, B, C);

    foreach (int val in res){
        
        Console.Write(val + " ");
    }
}

}

JavaScript

// JavaScript Code to Sort array after applying // equation using Brute Force Approach

// Function to apply quadratic transformation function evaluate(x, A, B, C) { return A * x * x + B * x + C; }

// Function to transform and sort the array in-place function sortArray(arr, A, B, C) { let n = arr.length;

let transformed = [];
// Apply the transformation in-place
for (let i = 0; i < n; i++) {
    transformed.push(evaluate(arr[i], A, B, C));
}

// Sort the transformed array
transformed.sort((a, b) => a - b);

return transformed;

}

// Driver Code let arr = [-4, -2, 0, 2, 4]; let A = 1, B = 3, C = 5;

let res = sortArray(arr, A, B, C);

for (let val of res) { process.stdout.write(val + " "); }

`

**[Expected Approach] Using Two Pointers - O(n) Time and O(n) Space

The **idea is to use the fact that input array is sorted and apply a **Two-Pointer approach. After applying the quadratic transformation to each element, the smallest and largest values will always be at the **ends of the array (Why? The equation given is parabolic. So the result of applying it to a sorted array will result in an array that will have a maximum/minimum with the sub-arrays to its left and right sorted)

We process from both ends using **two pointers (left and right) moving towards each other. By comparing the transformed values of **arr[left] and **arr[right], we can fill a new array (newArr) starting either from the front or the back depending on whether the **coefficient A is positive or negative. The observation here is:

• if **A >= 0, the largest values will be at the end
• while if **A < 0, the largest values will be at the beginning.

There are two distinct cases when working with a quadratic transformation of a sorted array, and the nature of the function depends on the coefficient **A.

**Case 1: A > 0 – Convex parabola (opens upwards) → **Has a valley (minimum point)

• The largest transformed values lie at the ends of the array.
• We fill the result array **from end to start using two pointers.

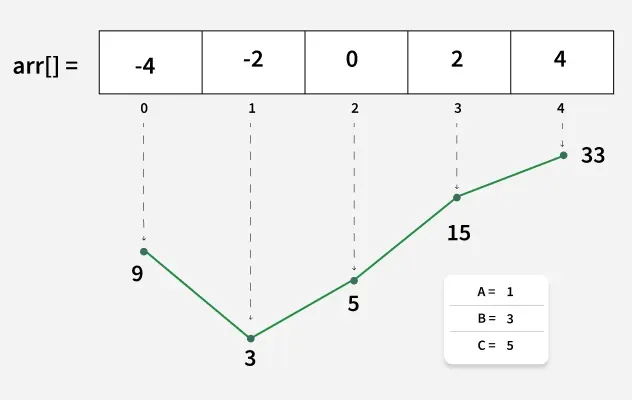
**Case 2: A < 0 – Concave parabola (opens downwards) → **Has a peak (maximum point)

• The smallest transformed values lie at the ends.
• We fill the result array **from start to end using two pointers.

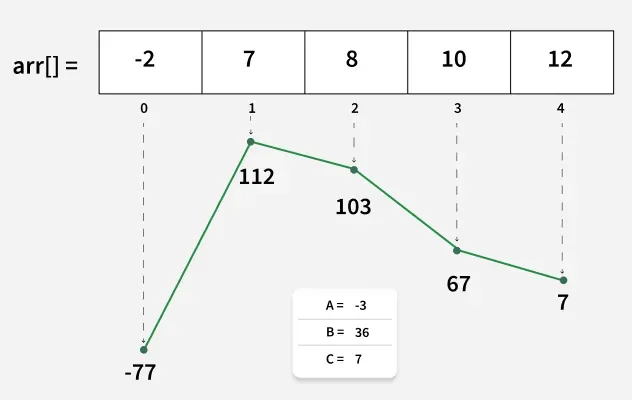
**Step-by-Step Implementation:

• Start by initializing two pointers: **left at the beginning and **right at the end of the array.
• Create a new array **newArr of the same size to store the transformed and sorted values.
• Determine the **index where you will start filling **newArr based on whether **A is positive or negative.
• Loop through the array using the **left and **right pointers, comparing the transformed values of **arr[left] and **arr[right].
• Depending on the sign of **A, place the larger of the two values at the appropriate position in **newArr.
• After processing all elements, copy the sorted values from **newArr back to the original **arr.
• Finally, return the modified **arr containing the transformed and sorted values.

**Illustration:

C++ `

#include <bits/stdc++.h> using namespace std;

// Function to apply quadratic transformation int evaluate(int x, int A, int B, int C) { return A * x * x + B * x + C; }

// Function to transform and sort the array vector sortArray(vector &arr, int A, int B, int C) { int n = arr.size(); vector newArr(n);

int left = 0, right = n - 1;
int index = (A >= 0) ? n - 1 : 0;

// Two-pointer approach to fill newArr 
while (left <= right) {
    int leftVal = evaluate(arr[left], A, B, C);
    int rightVal = evaluate(arr[right], A, B, C);

    if (A >= 0) {
        if (leftVal > rightVal) {
            newArr[index--] = leftVal;
            left++;
        } else {
            newArr[index--] = rightVal;
            right--;
        }
    } else {
        if (leftVal < rightVal) {
            newArr[index++] = leftVal;
            left++;
        } else {
            newArr[index++] = rightVal;
            right--;
        }
    }
}

return newArr;

}

int main() { vector arr = {-4, -2, 0, 2, 4}; int A = 1, B = 3, C = 5;

vector<int> res = sortArray(arr, A, B, C);

for (int val : res) {
    cout << val << " ";
}

return 0;

}

Java

import java.util.*;

class GfG {

// Function to apply quadratic transformation
public static int evaluate(int x, int A, int B, int C) {
    return A * x * x + B * x + C;
}

// Function to transform and sort the array
public static ArrayList<Integer> sortArray(int[] arr, int A, int B, int C) {
    int n = arr.length;
    int[] newArr = new int[n];

    int left = 0, right = n - 1;
    int index = (A >= 0) ? n - 1 : 0;

    // Two-pointer approach to fill newArr from end or start
    while (left <= right) {
        int leftVal = evaluate(arr[left], A, B, C);
        int rightVal = evaluate(arr[right], A, B, C);

        if (A >= 0) {
            if (leftVal > rightVal) {
                newArr[index--] = leftVal;
                left++;
            } else {
                newArr[index--] = rightVal;
                right--;
            }
        } else {
            if (leftVal < rightVal) {
                newArr[index++] = leftVal;
                left++;
            } else {
                newArr[index++] = rightVal;
                right--;
            }
        }
    }

    // Convert array to ArrayList and return
    ArrayList<Integer> result = new ArrayList<>();
    for (int val : newArr) {
        result.add(val);
    }

    return result;
}

public static void main(String[] args) {
    int[] arr = {-4, -2, 0, 2, 4};
    int A = 1, B = 3, C = 5;

    ArrayList<Integer> res = sortArray(arr, A, B, C);

    for (int val : res) {
        System.out.print(val + " ");
    }
}

}

Python

Python Code to Sort array after applying

equation using Two Pointer Approach

Function to apply quadratic transformation

def evaluate(x, A, B, C): return A * x * x + B * x + C

Function to transform and sort the array

def sortArray(arr, A, B, C): n = len(arr) newArr = [0] * n

left, right = 0, n - 1
index = n - 1 if A >= 0 else 0

# Two-pointer approach to fill newArr
# from end or start
while left <= right:
    leftVal = evaluate(arr[left], A, B, C)
    rightVal = evaluate(arr[right], A, B, C)

    if A >= 0:
        # Fill from end
        if leftVal > rightVal:
            newArr[index] = leftVal
            left += 1
            index -= 1
        else:
            newArr[index] = rightVal
            right -= 1
            index -= 1
    else:
        # Fill from start
        if leftVal < rightVal:
            newArr[index] = leftVal
            left += 1
            index += 1
        else:
            newArr[index] = rightVal
            right -= 1
            index += 1

return newArr

if name == "main": arr = [-4, -2, 0, 2, 4] A = 1 B = 3 C = 5

res = sortArray(arr, A, B, C)
print(*res)

C#

using System; using System.Collections.Generic;

class GfG {

// Function to apply quadratic transformation
public static int evaluate(int x, int A, int B, int C) {
    return A * x * x + B * x + C;
}

// Function to transform and sort the array
public static List<int> sortArray(int[] arr, int A, int B, int C) {
    int n = arr.Length;
    int[] newArr = new int[n];

    int left = 0, right = n - 1;
    int index = (A >= 0) ? n - 1 : 0;

    // Two-pointer approach to fill newArr
    while (left <= right) {
        int leftVal = evaluate(arr[left], A, B, C);
        int rightVal = evaluate(arr[right], A, B, C);

        if (A >= 0) {
            if (leftVal > rightVal) {
                newArr[index--] = leftVal;
                left++;
            } else {
                newArr[index--] = rightVal;
                right--;
            }
        } else {
            if (leftVal < rightVal) {
                newArr[index++] = leftVal;
                left++;
            } else {
                newArr[index++] = rightVal;
                right--;
            }
        }
    }

    return new List<int>(newArr);
}

public static void Main(string[] args) {
    int[] arr = {-4, -2, 0, 2, 4};
    int A = 1, B = 3, C = 5;

    List<int> res = sortArray(arr, A, B, C);

    foreach (int val in res) {
        Console.Write(val + " ");
    }
}

}

JavaScript

// JavaScript Code to Sort array after applying // equation using Two Pointer Approach

// Function to apply quadratic transformation function evaluate(x, A, B, C) { return A * x * x + B * x + C; }

// Function to transform and sort the array function sortArray(arr, A, B, C) { let n = arr.length; let newArr = new Array(n);

let left = 0, right = n - 1;
let index = (A >= 0) ? n - 1 : 0;

// Two-pointer approach to fill newArr
// from end or start
while (left <= right) {
    let leftVal = evaluate(arr[left], A, B, C);
    let rightVal = evaluate(arr[right], A, B, C);

    if (A >= 0) {
        // Fill from end
        if (leftVal > rightVal) {
            newArr[index] = leftVal;
            left++;
            index--;
        } else {
            newArr[index] = rightVal;
            right--;
            index--;
        }
    } else {
        // Fill from start
        if (leftVal < rightVal) {
            newArr[index] = leftVal;
            left++;
            index++;
        } else {
            newArr[index] = rightVal;
            right--;
            index++;
        }
    }
}

// Assign values back to arr
for (let i = 0; i < n; i++) {
    arr[i] = newArr[i];
}

return arr;

}

// Driver Code let arr = [-4, -2, 0, 2, 4]; let A = 1, B = 3, C = 5;

let res = sortArray(arr, A, B, C);

console.log(res.join(' '));

`