Tiling Problem (original) (raw)

Last Updated : 16 Dec, 2024

Try it on GfG Practice

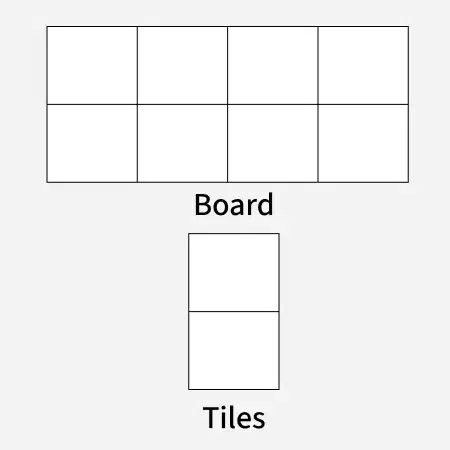
Given a "2 x n" board and **tiles of size "2 x 1", the task is to **count the number of ways to tile the given board using the **2 x 1 tiles. A tile can either be placed **horizontally i.e., as a 1 x 2 tile or **vertically i.e., as 2 x 1 tile.

**Examples:

**Input: n = 4
**Output: 5
**Explanation: For a 2 x 4 board, there are 5 ways

• All 4 vertical (1 way)
• All 4 horizontal (1 way)
• 2 vertical and 2 horizontal (3 ways)

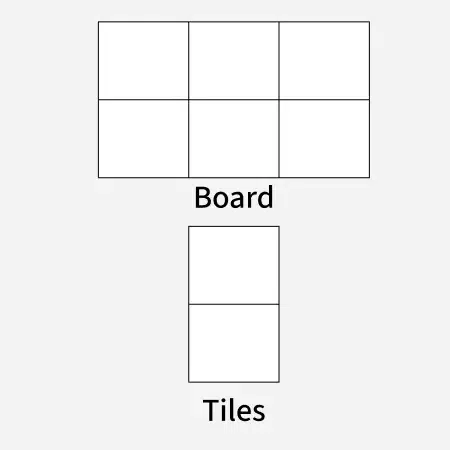
**Input: n = 3
**Output: 3
**Explanation: We need 3 tiles to tile the board of size 2 x 3.
We can tile the board using the following ways

• Place all 3 tiles vertically.
• Place 1 tile vertically and the remaining 2 tiles horizontally (2 ways)

Table of Content

• Using Recursion - O(2^n) Time and O(n) Space
• Using Top-Down DP (Memoization) - O(n) Time and O(n) Space
• Using Bottom-Up DP (Tabulation) - O(n) Time and O(n) Space
• Using Space Optimized DP - O(n) Time and O(1) Space

Using Recursion - O(2^n) Time and O(n) Space

The idea is to explore **two possible ways to place tiles on a **2 x n board: either placing a **vertical tile (2 x 1) which reduces the problem to filling a 2 x (n-1) board, or placing **two horizontal tiles (1 x 2) which reduces the problem to filling a **2 x (n-2) board. At each step, we **sum these two possibilities, creating a recursive solution where the total number of ways to tile the board is the sum of ways for the smaller subproblems.

Mathematically the recurrence relation will look like the following:

**numberOfWays(n) = numberOfWays(n-1) + numberOfWays(n-2).

**Base Cases:

• numberOfWays(n) = 1, if n = 0.
• numberOfWays(n) = 0, if n < 0.

C++ `

// C++ program to implement // tiling problem using recursion #include <bits/stdc++.h> using namespace std;

int numberOfWays(int n) {

// Base Case: invalid n 
if (n<0) return 0;

// Base case: valid n 
if (n == 0) return 1;

int ans = 0;

// count ways if one tile 
// is placed vertically
ans = numberOfWays(n-1);

// count ways if two tiles 
// are placed horizontly.
ans += numberOfWays(n-2);

return ans;

}

int main() { int n = 4; cout<<numberOfWays(n);

return 0;

}

Java

// Java program to implement // tiling problem using recursion

class GfG {

static int numberOfWays(int n) {
    
    // Base Case: invalid n 
    if (n < 0) return 0;
    
    // Base case: valid n 
    if (n == 0) return 1;
    
    int ans = 0;
    
    // count ways if one tile 
    // is placed vertically
    ans = numberOfWays(n - 1);
    
    // count ways if two tiles 
    // are placed horizontally.
    ans += numberOfWays(n - 2);
    
    return ans;
}

public static void main(String[] args) {
    int n = 4;
    System.out.println(numberOfWays(n));
}

}

Python

Python program to implement

tiling problem using recursion

def numberOfWays(n):

# Base Case: invalid n 
if n < 0:
    return 0

# Base case: valid n 
if n == 0:
    return 1

ans = 0

# count ways if one tile 
# is placed vertically
ans = numberOfWays(n - 1)

# count ways if two tiles 
# are placed horizontally.
ans += numberOfWays(n - 2)

return ans

if name == "main": n = 4 print(numberOfWays(n))

C#

// C# program to implement // tiling problem using recursion

using System;

class GfG {

static int numberOfWays(int n) {
    
    // Base Case: invalid n 
    if (n < 0) return 0;
    
    // Base case: valid n 
    if (n == 0) return 1;
    
    int ans = 0;
    
    // count ways if one tile 
    // is placed vertically
    ans = numberOfWays(n - 1);
    
    // count ways if two tiles 
    // are placed horizontally.
    ans += numberOfWays(n - 2);
    
    return ans;
}

static void Main(string[] args) {
    int n = 4;
    Console.WriteLine(numberOfWays(n));
}

}

JavaScript

// JavaScript program to implement // tiling problem using recursion

function numberOfWays(n) {

// Base Case: invalid n 
if (n < 0) return 0;

// Base case: valid n 
if (n === 0) return 1;

let ans = 0;

// count ways if one tile 
// is placed vertically
ans = numberOfWays(n - 1);

// count ways if two tiles 
// are placed horizontally.
ans += numberOfWays(n - 2);

return ans;

}

const n = 4; console.log(numberOfWays(n));

`

Using Top-Down DP (Memoization) - O(n) Time and O(n) Space

If we notice carefully, we can observe that the above recursive solution holds the following two properties of Dynamic Programming:

**1. Optimal Substructure: Number of ways to add **i'th tile, i.e., **numberOfWays(i), depends on the optimal solutions of the subproblems **numberOfWays(i-1), and **numberOfWays(i-2). By comparing these optimal substructures, we can efficiently calculate the number of ways to add i' th tile.

**2. Overlapping Subproblems: While applying a recursive approach in this problem, we notice that certain subproblems are computed multiple times. For example, for n = 4, **numberOfWays(3) and numberOfWays(2) are called. **numberOfWays(3) again calls numberOfWays(2) which leads to Overlapping Subproblems.

• There are only is **one parameter: i that changes in the recursive solution. So we create a **1D array of size n+1 for memoization.
• We initialize this **array as -1 to indicate nothing is computed initially.
• Now we modify our recursive solution to first check if the value is -1, then only make recursive calls. This way, we avoid re-computations of the same subproblems. C++ `

// C++ program to implement // tiling problem using memoization #include <bits/stdc++.h> using namespace std;

int countRecur(int n, vector &memo) {

// Base Case: invalid n 
if (n<0) return 0;

// Base case: valid n 
if (n == 0) return 1;

// If value is memoized
if (memo[n] != -1) return memo[n];

int ans = 0;

// count ways if one tile 
// is placed vertically
ans = countRecur(n-1, memo);

// count ways if two tiles 
// are placed horizontly.
ans += countRecur(n-2, memo);

return memo[n] = ans;

}

int numberOfWays(int n) { vector memo(n+1, -1); return countRecur(n, memo); }

int main() { int n = 4; cout<<numberOfWays(n);

return 0;

}

Java

// Java program to implement // tiling problem using memoization import java.util.Arrays;

class GfG {

static int countRecur(int n, int[] memo) {
    
    // Base Case: invalid n 
    if (n < 0) return 0;
    
    // Base case: valid n 
    if (n == 0) return 1;
    
    // If value is memoized
    if (memo[n] != -1) return memo[n];
    
    int ans = 0;
    
    // count ways if one tile 
    // is placed vertically
    ans = countRecur(n - 1, memo);
    
    // count ways if two tiles 
    // are placed horizontally.
    ans += countRecur(n - 2, memo);
    
    return memo[n] = ans;
}

static int numberOfWays(int n) {
    int[] memo = new int[n + 1];
    Arrays.fill(memo, -1);
    return countRecur(n, memo);
}

public static void main(String[] args) {
    int n = 4;
    System.out.println(numberOfWays(n));
}

}

Python

Python program to implement

tiling problem using memoization

def countRecur(n, memo):

# Base Case: invalid n 
if n < 0:
    return 0

# Base case: valid n 
if n == 0:
    return 1

# If value is memoized
if memo[n] != -1:
    return memo[n]

ans = 0

# count ways if one tile 
# is placed vertically
ans = countRecur(n - 1, memo)

# count ways if two tiles 
# are placed horizontally.
ans += countRecur(n - 2, memo)

memo[n] = ans
return memo[n]

def numberOfWays(n): memo = [-1] * (n + 1) return countRecur(n, memo)

if name == "main": n = 4 print(numberOfWays(n))

C#

// C# program to implement // tiling problem using memoization

using System;

class GfG {

static int countRecur(int n, int[] memo) {
    
    // Base Case: invalid n 
    if (n < 0) return 0;
    
    // Base case: valid n 
    if (n == 0) return 1;
    
    // If value is memoized
    if (memo[n] != -1) return memo[n];
    
    int ans = 0;
    
    // count ways if one tile 
    // is placed vertically
    ans = countRecur(n - 1, memo);
    
    // count ways if two tiles 
    // are placed horizontally.
    ans += countRecur(n - 2, memo);
    
    return memo[n] = ans;
}

static int numberOfWays(int n) {
    int[] memo = new int[n + 1];
    for (int i = 0; i <= n; i++) {
        memo[i] = -1;
    }
    return countRecur(n, memo);
}

static void Main(string[] args) {
    int n = 4;
    Console.WriteLine(numberOfWays(n));
}

}

JavaScript

// JavaScript program to implement // tiling problem using memoization

function countRecur(n, memo) {

// Base Case: invalid n 
if (n < 0) return 0;

// Base case: valid n 
if (n === 0) return 1;

// If value is memoized
if (memo[n] !== -1) return memo[n];

let ans = 0;

// count ways if one tile 
// is placed vertically
ans = countRecur(n - 1, memo);

// count ways if two tiles 
// are placed horizontally.
ans += countRecur(n - 2, memo);

return memo[n] = ans;

}

function numberOfWays(n) { const memo = Array(n + 1).fill(-1); return countRecur(n, memo); }

const n = 4; console.log(numberOfWays(n));

`

Using Bottom-Up DP (Tabulation) - O(n) Time and O(n) Space

The idea is to fill the **DP table based on **previous values. For each tile, we either **add it **vertically or **horizontally to computenumber of ways. The table is filled in an iterative manner from i = 2 to n.

The dynamic programming relation is as follows:

• **dp[i] = dp[i-1] + dp[i-2]

C++ `

// C++ program to implement // tiling problem using tabulation #include <bits/stdc++.h> using namespace std;

int numberOfWays(int n) { if (n==0 || n==1) return 1;

vector<int> dp(n+1);

dp[0] = 1;
dp[1] = 1;

for (int i=2; i<=n; i++) {
    dp[i] = dp[i-1] + dp[i-2];
}

return dp[n];

}

int main() { int n = 4; cout<<numberOfWays(n);

return 0;

}

Java

// Java program to implement // tiling problem using tabulation

import java.util.*;

class GfG {

static int numberOfWays(int n) {
    if (n == 0 || n == 1) return 1;
    
    int[] dp = new int[n + 1];
    
    dp[0] = 1;
    dp[1] = 1;
    
    for (int i = 2; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    
    return dp[n];
}

public static void main(String[] args) {
    int n = 4;
    System.out.println(numberOfWays(n));
}

}

Python

Python program to implement

tiling problem using tabulation

def numberOfWays(n): if n == 0 or n == 1: return 1

dp = [0] * (n + 1)

dp[0] = 1
dp[1] = 1

for i in range(2, n + 1):
    dp[i] = dp[i - 1] + dp[i - 2]

return dp[n]

if name == "main": n = 4 print(numberOfWays(n))

C#

// C# program to implement // tiling problem using tabulation

using System;

class GfG {

static int numberOfWays(int n) {
    if (n == 0 || n == 1) return 1;
    
    int[] dp = new int[n + 1];
    
    dp[0] = 1;
    dp[1] = 1;
    
    for (int i = 2; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    
    return dp[n];
}

static void Main(string[] args) {
    int n = 4;
    Console.WriteLine(numberOfWays(n));
}

}

JavaScript

// JavaScript program to implement // tiling problem using tabulation

function numberOfWays(n) { if (n === 0 || n === 1) return 1;

const dp = new Array(n + 1).fill(0);

dp[0] = 1;
dp[1] = 1;

for (let i = 2; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
}

return dp[n];

}

const n = 4; console.log(numberOfWays(n));

`

Using Space Optimized DP - O(n) Time and O(1) Space

In **previous approach of dynamic programming we have derived the relation between states as given below:

• **dp[i] = dp[i-1] + dp[i-2]

If we observe that for calculating **current dp[i] state we only need **dp[i-1] and **dp[i-2]. There is no need to store all the **previous states just **two previous state is used to compute result.

C++ `

// C++ program to implement // tiling problem using space optimised dp #include <bits/stdc++.h> using namespace std;

int numberOfWays(int n) { if (n==0 || n==1) return 1;

int prev2 = 1;
int prev1 = 1;

for (int i=2; i<=n; i++) {
    int curr = prev1+prev2;
    
    prev2 = prev1;
    prev1 = curr;
}

return prev1;

}

int main() { int n = 4; cout<<numberOfWays(n);

return 0;

}

Java

// Java program to implement // tiling problem using space optimised dp

import java.util.*;

class GfG {

static int numberOfWays(int n) {
    if (n == 0 || n == 1) return 1;
    
    int prev2 = 1;
    int prev1 = 1;
    
    for (int i = 2; i <= n; i++) {
        int curr = prev1 + prev2;
        
        prev2 = prev1;
        prev1 = curr;
    }
    
    return prev1;
}

public static void main(String[] args) {
    int n = 4;
    System.out.println(numberOfWays(n));
}

}

Python

Python program to implement

tiling problem using space optimised dp

def numberOfWays(n): if n == 0 or n == 1: return 1

prev2 = 1
prev1 = 1

for i in range(2, n + 1):
    curr = prev1 + prev2
    prev2 = prev1
    prev1 = curr

return prev1

if name == "main": n = 4 print(numberOfWays(n))

C#

// C# program to implement // tiling problem using space optimised dp

using System;

class GfG {

static int numberOfWays(int n) {
    if (n == 0 || n == 1) return 1;
    
    int prev2 = 1;
    int prev1 = 1;
    
    for (int i = 2; i <= n; i++) {
        int curr = prev1 + prev2;
        
        prev2 = prev1;
        prev1 = curr;
    }
    
    return prev1;
}

static void Main(string[] args) {
    int n = 4;
    Console.WriteLine(numberOfWays(n));
}

}

JavaScript

// JavaScript program to implement // tiling problem using space optimised dp

function numberOfWays(n) { if (n === 0 || n === 1) return 1;

let prev2 = 1;
let prev1 = 1;

for (let i = 2; i <= n; i++) {
    let curr = prev1 + prev2;
    prev2 = prev1;
    prev1 = curr;
}

return prev1;

}

const n = 4; console.log(numberOfWays(n));

`

**Related articles:

• Nth Fibonacci Number
• Count the number of ways to tile the floor of size n x m using 1 x m size tiles