Time and Space Complexity Analysis of Quick Sort (original) (raw)
Last Updated : 18 Nov, 2024
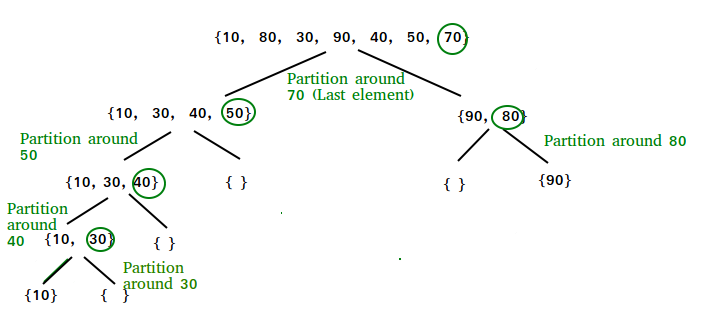
The **time complexity of **Quick Sort is **O(n log n) on **average case, but can become **O(n^2) in the **worst-case. The **space complexity of **Quick Sort in the **best case is **O(log n), while in the **worst-case scenario, it becomes **O(n) due to unbalanced partitioning causing a skewed recursion tree that requires a call stack of size O(n).
Quick Sort Algorithm
| Variation | Time Complexity | Auxiliary Space |
|---|---|---|
| Best Case | O(n log n) | O(log n) |
| Average Case | O(n log n) | O(log n) |
| Worst Case | O(n^2) | O(n) |
Time Complexity Analysis of Quick Sort:
Let us consider the following terminologies:
**T(K): Time complexity of quicksort of K elements
**P(K): Time complexity for finding the position of pivot among K elements.
Best Case Time Complexity Analysis of Quick Sort: **O(N * logN)
The best case occurs when we select the pivot as the mean. So here
T(N) = 2 * T(N / 2) + N * constant
Now T(N/2) is also 2*T(N / 4) + N / 2 * constant. So,
T(N) = 2*(2*T(N / 4) + N / 2 * constant) + N * constant
= 4 * T(N / 4) + 2 * constant * N.
So, we can say that
T(N) = 2k * T(N / 2k) + k * constant * N
then, 2k = N
k = log2N
So **T(N) = N * T(1) + N * log 2 N. Therefore, the time complexity is **O(N * logN).
Worst Case Time Complexity Analysis of Quick Sort: **O(N 2 ).
The worst case will occur when the array gets divided into two parts, one part consisting of N-1 elements and the other and so on. So,
T(N) = T(N - 1) + N * constant
= T(N - 2) + (N - 1) * constant + N * constant = T(N - 2) + 2 * N * constant - constant
= T(N - 3) + 3 * N * constant - 2 * constant - constant
. . .
= T(N - k) + k * N * constant - (k - 1) * constant - . . . - 2*constant - constant
= T(N - k) + k * N * constant - constant * (k*(k - 1))/2
If we put k = N in the above equation, then
T(N) = T(0) + N * N * constant - constant * (N * (N-1)/2)
= N2 - N*(N-1)/2
= N2/2 + N/2
So the worst case complexity is **O(N 2 )
Average Case Time Complexity Analysis of Quick Sort: **O(N * logN)
For the average case consider the array gets divided into two parts of size **k and ****(N-k)**. So,
T(N) = T(N - k) + T(k)
= 1 / N * [ \sum_{i = 1}^{N-1} T(i) + \sum_{i = 1}^{N-1} T(N-i) ]
As \sum_{i = 1}^{N-1} T(i) and \sum_{i = 1}^{N-1} T(N-i) are equal likely functions, we can say
T(N) = 2/N * [ \sum_{i = 1}^{N-1} T(i) ]
N * T(N) = 2 * [ \sum_{i = 1}^{N-1} T(i) ]
Also, we can write
(N - 1) * T(N - 1) = 2 * [ \sum_{i = 1}^{N-2} T(i) ]
If we subtract the above two equations, we get
N * T(N) - (N - 1) * T(N - 1) = 2 * T(N - 1) + N2 * constant - (N - 1)2 * constant
N * T(N) = T(N - 1) * (2 + N - 1) + constant + 2 * N * constant - constant
= (N + 1) * T(N - 1) + 2 * N * constant
Divide both side by N*(N-1) and we will get
T(N) / (N + 1) = T(N - 1)/N + 2 * constant / (N + 1) --- (i)
If we put N = N-1 it becomes
T(N - 1) / N = T(N - 2)/(N - 1) + 2*constant/N
Therefore, the equation (i) can be written as
T(N) / (N + 1) = T(N - 2)/(N - 1) + 2*constant/(N + 1) + 2*constant/N
Similarly, we can get the value of T(N-2) by replacing N by (N-2) in the equation (i). At last it will be like
T(N) / (N + 1) = T(1)/2 + 2*constant * [1/2 + 1/3 + . . . + 1/(N - 1) + 1/N + 1/(N + 1)]
T(N) = 2 * constant * log2N * (N + 1)
If we ignore the constant it becomes
T(N) = log2N * (N + 1)
So the time complexity is **O(N * logN).
Space Analysis of Quick Sort:
**Worst-case scenario: **O(n) due to unbalanced partitioning leading to a skewed recursion tree requiring a call stack of size O(n).
**Best-case scenario: O(log n) as a result of balanced partitioning leading to a balanced recursion tree with a call stack of size O(log n).