Vertical Traversal of a Binary Tree (original) (raw)
Last Updated : 04 Feb, 2025
Given a **Binary Tree, the task is to find its vertical traversal starting from the **leftmost level to the **rightmost level. If multiple nodes pass through a vertical line, they should be printed as they appear in the **level order traversal of the tree.
**Examples:
**Input:
**Output: [[4], [2], [1, 5, 6], [3, 8], [7], [9]]
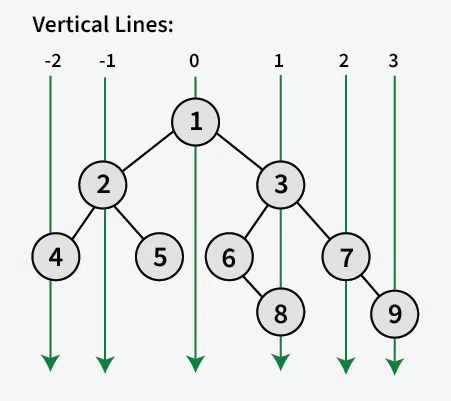
**Explanation: The below image shows the horizontal distances used to print vertical traversal starting from the leftmost level to the rightmost level.
Table of Content
- Brute Force Approach - O(n^2) Time and O(n) Space
- Using map - O(n*log n) Time and O(n) Space
- Using Hashmap - O(n) Time and O(n) Space
**[Naive Approach] - O(n^2) Time and O(n) Space
The idea is to traverse the tree once and get the **minimum and maximum horizontal distance with respect to **root. For the tree shown above, minimum distance is **-2 (for node with value 4) and **maximum distance is **3 (For node with value 9).
Once we have **maximum and **minimum distances from root, we iterate for each vertical line at distance **minimum to **maximum from root, and for each vertical line traverse the tree and return the nodes which lie on that vertical line. Please refer to Vertical Order using Brute Force for this approach.
**[Expected Approach - 1] Using DFS and Hashmap - O(n) Time and O(n) Space
The idea is to traverse the tree using **dfs and maintain a **hash map to store nodes at each horizontal distance (HD) from the root. Starting with an HD of 0 at the root, the HD is **decremented for left children and **incremented for right children. As we traverse, we **add each node's value to the **map based on its **HD. Finally, we **collect the nodes from the map in **increasing order of HD to produce the vertical order of the tree.
C++ `
//Driver Code Starts // C++ code for Vertical Traversal of a Binary Tree // using HashMap and DFS (Depth First Search)
#include #include #include using namespace std;
class Node { public: int data; Node *left, *right;
Node(int x) {
data = x;
left = nullptr;
right = nullptr;
}}; //Driver Code Ends
// Helper function to perform DFS and // store nodes at different horizontal distances void DFS(Node* root, int hd, int &mn, unordered_map<int, vector> &mp) { if (root == nullptr) return;
// Store the current node in the map at horizontal distance hd
mp[hd].push_back(root->data);
// Update the minimum horizontal distance
mn = min(mn, hd);
// Recursively traverse the left and right subtrees
DFS(root->left, hd - 1, mn, mp);
DFS(root->right, hd + 1, mn, mp);}
// Function to perform vertical order traversal of a binary tree vector<vector> verticalOrder(Node *root) {
// HashMap to store nodes at each horizontal distance
unordered_map<int, vector<int>> mp;
// Variable to track the minimum horizontal distance
int mn = 0;
// Perform DFS to fill the hashmap with vertical levels
DFS(root, 0, mn, mp);
vector<vector<int>> res;
int hd = mn;
// Traverse the map from minimum to maximum horizontal distance
while(mp.find(hd) != mp.end()) {
res.push_back(mp[hd]);
hd++;
}
return res;}
//Driver Code Starts int main() {
// Constructing the binary tree:
// 1
// / \
// 2 3
// / \ / \
// 4 5 6 7
// \ \
// 8 9
Node *root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->right->left = new Node(6);
root->right->right = new Node(7);
root->right->left->right = new Node(8);
root->right->right->right = new Node(9);
vector<vector<int>> res = verticalOrder(root);
for(vector<int> temp: res) {
cout << "[ ";
for (int val: temp)
cout << val << " ";
cout << "] ";
}
return 0;}
//Driver Code Ends
Java
//Driver Code Starts // Java code for Vertical Traversal of a Binary Tree // using HashMap, DFS, and ArrayList
import java.util.*;
class Node { int data; Node left, right;
Node(int x) {
data = x;
left = null;
right = null;
}}
class GfG { //Driver Code Ends
// Helper function to perform DFS and
// store nodes at different horizontal distances
static void DFS(Node root, int hd, int[] mn,
HashMap<Integer, ArrayList<Integer>> mp) {
if (root == null)
return;
// Store the current node in the map at horizontal distance hd
if (!mp.containsKey(hd))
mp.put(hd, new ArrayList<>());
mp.get(hd).add(root.data);
// Update the minimum horizontal distance
mn[0] = Math.min(mn[0], hd);
// Recursively traverse the left and right subtrees
DFS(root.left, hd - 1, mn, mp);
DFS(root.right, hd + 1, mn, mp);
}
// Function to perform vertical order traversal of a binary tree
static ArrayList<ArrayList<Integer>> verticalOrder(Node root) {
// HashMap to store nodes at each horizontal distance
HashMap<Integer, ArrayList<Integer>> mp = new HashMap<>();
// Array to track the minimum horizontal distance (mutable)
int[] mn = {0};
// Perform DFS to fill the hashmap with vertical levels
DFS(root, 0, mn, mp);
ArrayList<ArrayList<Integer>> res = new ArrayList<>();
int hd = mn[0];
// Traverse the map from minimum to maximum horizontal distance
while (mp.containsKey(hd)) {
res.add(mp.get(hd));
hd++;
}
return res;
}//Driver Code Starts
public static void main(String[] args) {
// Constructing the binary tree:
// 1
// /
// 2 3
// / \ /
// 4 5 6 7
// \
// 8 9
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
root.right.right.right = new Node(9);
ArrayList<ArrayList<Integer>> res = verticalOrder(root);
for (ArrayList<Integer> temp : res) {
System.out.print("[ ");
for (int val : temp)
System.out.print(val + " ");
System.out.print("] ");
}
}}
//Driver Code Ends
Python
#Driver Code Starts
Python code for Vertical Traversal of a Binary Tree
using HashMap and DFS (Depth First Search)
class Node: def init(self, x): self.data = x self.left = None self.right = None #Driver Code Ends
Helper function to perform DFS and
store nodes at different horizontal distances
def DFS(root, hd, mn, mp): if root is None: return
# Store the current node in the map at horizontal distance hd
if hd not in mp:
mp[hd] = []
mp[hd].append(root.data)
# Update the minimum horizontal distance
mn[0] = min(mn[0], hd)
# Recursively traverse the left and right subtrees
DFS(root.left, hd - 1, mn, mp)
DFS(root.right, hd + 1, mn, mp)Function to perform vertical order traversal of a binary tree
def verticalOrder(root): # Dictionary to store nodes at each horizontal distance mp = {}
# List to track the minimum horizontal distance (mutable)
mn = [0]
# Perform DFS to fill the dictionary with vertical levels
DFS(root, 0, mn, mp)
res = []
hd = mn[0]
# Traverse the dictionary from minimum to maximum horizontal distance
while hd in mp:
res.append(mp[hd])
hd += 1
return res#Driver Code Starts
if name == "main":
# Constructing the binary tree:
# 1
# /
# 2 3
# / \ /
# 4 5 6 7
# \
# 8 9
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
root.right.left.right = Node(8)
root.right.right.right = Node(9)
res = verticalOrder(root)
for temp in res:
print("[", " ".join(map(str, temp)), "]", end=" ")#Driver Code Ends
C#
//Driver Code Starts // C# code for Vertical Traversal of a Binary Tree // using Dictionary and DFS (Depth First Search)
using System; using System.Collections.Generic;
class Node { public int data; public Node left, right;
public Node(int x) {
data = x;
left = null;
right = null;
}}
class GfG { //Driver Code Ends
// Helper function to perform DFS and
// store nodes at different horizontal distances
static void DFS(Node root, int hd, ref int mn, Dictionary<int, List<int>> mp) {
if (root == null)
return;
// Store the current node in the dictionary at horizontal distance hd
if (!mp.ContainsKey(hd))
mp[hd] = new List<int>();
mp[hd].Add(root.data);
// Update the minimum horizontal distance
mn = Math.Min(mn, hd);
// Recursively traverse the left and right subtrees
DFS(root.left, hd - 1, ref mn, mp);
DFS(root.right, hd + 1, ref mn, mp);
}
// Function to perform vertical order traversal of a binary tree
static List<List<int>> verticalOrder(Node root) {
// Dictionary to store nodes at each horizontal distance
Dictionary<int, List<int>> mp = new Dictionary<int, List<int>>();
// Variable to track the minimum horizontal distance
int mn = 0;
// Perform DFS to fill the dictionary with vertical levels
DFS(root, 0, ref mn, mp);
List<List<int>> res = new List<List<int>>();
int hd = mn;
// Traverse the dictionary from minimum to maximum horizontal distance
while (mp.ContainsKey(hd)) {
res.Add(mp[hd]);
hd++;
}
return res;
}//Driver Code Starts static void Main() { // Constructing the binary tree: Node root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.left = new Node(6); root.right.right = new Node(7); root.right.left.right = new Node(8); root.right.right.right = new Node(9);
List<List<int>> res = verticalOrder(root);
foreach (var temp in res) {
Console.Write("[ ");
foreach (var val in temp)
Console.Write(val + " ");
Console.Write("] ");
}
}} //Driver Code Ends
JavaScript
//Driver Code Starts // JavaScript code for Vertical Traversal of a Binary Tree // using HashMap and DFS (Depth First Search)
class Node { constructor(x) { this.data = x; this.left = null; this.right = null; } } //Driver Code Ends
// Helper function to perform DFS and // store nodes at different horizontal distances function DFS(root, hd, mn, mp) { if (root === null) return;
// Store the current node in the map at horizontal distance hd
if (!mp.has(hd))
mp.set(hd, []);
mp.get(hd).push(root.data);
// Update the minimum horizontal distance
mn.val = Math.min(mn.val, hd);
// Recursively traverse the left and right subtrees
DFS(root.left, hd - 1, mn, mp);
DFS(root.right, hd + 1, mn, mp);}
// Function to perform vertical order traversal of a binary tree function verticalOrder(root) {
// Map to store nodes at each horizontal distance
let mp = new Map();
// Variable to track the minimum horizontal distance
let mn = { val: 0 };
// Perform DFS to fill the map with vertical levels
DFS(root, 0, mn, mp);
let res = [];
let hd = mn.val;
// Traverse the map from minimum to maximum horizontal distance
while (mp.has(hd)) {
res.push(mp.get(hd));
hd++;
}
return res;}
//Driver Code Starts // Driver Code
// Constructing the binary tree:
// 1
// /
// 2 3
// / \ /
// 4 5 6 7
// \
// 8 9
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
root.right.right.right = new Node(9);
let res = verticalOrder(root);
let output = ""; res.forEach(temp => { output += "[ "; temp.forEach(val => output += val + " "); output += "] "; }); console.log(output);
//Driver Code Ends
`
Output
[ 4 ] [ 2 ] [ 1 5 6 ] [ 3 8 ] [ 7 ] [ 9 ]
**[Expected Approach - 2] Using BFS and Hashmap - O(n) Time and O(n) Space
This approach is similar to the above approach but here we traverse the tree using BFS traversal.
Refer Vertical Traversal of a Binary Tree using BFS for detailed explanation.
**Related article: