What is Memoization? A Complete Tutorial (original) (raw)
Last Updated : 29 Nov, 2024
In this tutorial, we will dive into **memoization, a powerful optimization technique that can drastically improve the performance of certain algorithms. Memoization helps by storing the results of expensive function calls and reusing them when the same inputs occur again. This avoids redundant calculations, making your code more efficient.
The term "**Memoization" comes from the Latin word "**memorandum" (**to remember), which is commonly shortened to "**memo" in American English, and which means "**to transform the results of a function into something to remember".
In computing, **memoization is used to **speed up computer programs by eliminating the **repetitive computation of results, and by avoiding repeated calls to functions that process the same input.
Table of Content
- What is Memoization?
- Why is Memoization used?
- Where to use Memoization?
- Types of Memoization
- How Memoization technique is used in Dynamic Programming?
- How Memoization is different from Tabulation?
- Coding Practice Problems on Memoization
- Conclusion
**What is Memoization?
**Memoization is an optimization technique primarily used to enhance the performance of algorithms by **storing the results of expensive function calls and reusing them when the same inputs occur again. The term comes from "**memorandum", which refers to a note intended to help with memory.
Memoization is particularly effective in scenarios involving **repeated computations, like **recursive algorithms, where the same calculations may be performed multiple times.
Why is Memoization used?
**Memoization is a specific form of **caching that is used in **dynamic programming. The purpose of caching is to **improve the performance of our programs and keep data accessible that can be used later. It basically **stores the previously calculated result of the subproblem and **reuses the stored result for the same subproblem. This removes the extra effort to calculate again and again for the same problem.
Where to use Memoization?
**Memoization is useful in situations where **previously calculated results can be reused. It is particularly effective in **recursive problems, especially those involving **overlapping subproblems, where the same calculations are repeated multiple times.
Example of Memoization: Finding nth Fibonacci Number
The Fibonacci sequence is a **classic example of how **memoization can optimize **recursive algorithms by eliminating redundant computations.
The Fibonacci sequence is defined as:
**Base Case: F(0) = 0 and F(1) = 1
**Recursive Cases: F(n) = F(n-1) + F(n-2)Using **recursion, solving F(n) involves repeatedly breaking the problem into **smaller subproblems. However, **many of these subproblems are recalculated multiple times, leading to inefficiency. For instance, computing **F(5) will independently calculate F(3) and F(2) multiple times. By using memoization, **we store the results of already computed subproblems in a cache, allowing us to reuse them whenever the same subproblem arises again. This eliminates redundant calculations and significantly improves efficiency. Please refer to Nth Fibonacci Number for implementation.
**Without memoization, the time complexity of finding the nth Fibonacci number using recursion is **O(2^n), as the function repeatedly solves overlapping subproblems, creating an **exponential number of recursive calls. For instance, **F(3) and F(2) are recalculated **multiple times when computing F(5), leading to inefficiency. **With memoization, the time complexity reduces to O(n) because each Fibonacci number is computed **only once and stored for reuse. This eliminates redundant computations and ensures **a linear traversalfrom F(0) and F(n), significantly improving performance.
**Types of Memoization
The implementation of **memoization depends on the **parameters that change and are responsible for solving the problem. Memoization can be applied in various ways, based on the number of arguments in the recursive function. Below are some common types of memoization:
**1D Memoization: Used when the recursive function has **one argument whose value changes with every function call.
**2D Memoization: Used when the recursive function has **two arguments whose values change with every function call.
**3D Memoization: Used when the recursive function has **three arguments whose values change with every function call.
Please refer to Memoization (1D, 2D and 3D) for better understanding.
How Memoization technique is used in Dynamic Programming?
Dynamic programming helps to efficiently solve problems that have **overlapping subproblems and optimal substructure properties. The idea behind dynamic programming is to break the problem into **smaller sub-problems and save the result for future use, thus eliminating the need to compute the result repeatedly.
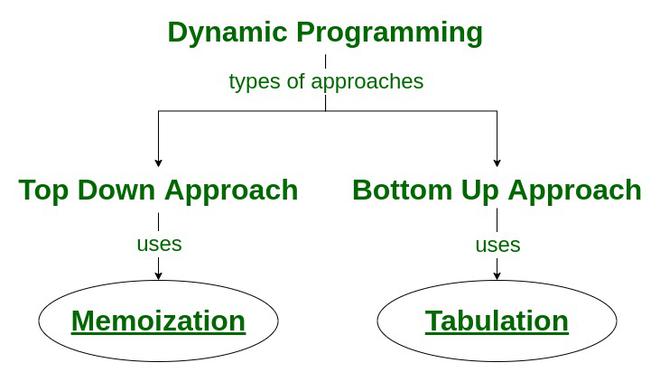
There are two approaches to formulate a dynamic programming solution:
- **Top-Down Approach: _This approach follows the **memoization technique. It consists of **recursion and **caching. In computation, recursion represents the process of calling functions repeatedly, whereas cache refers to the process of storing intermediate results.
- **Bottom-Up Approach: _This approach uses the **tabulation technique to implement the dynamic programming solution. It addresses the same problems as before, but without recursion. In this approach, iteration replaces recursion. Hence, there is **no stack overflow error or overhead of recursive procedures.
How Memoization technique is used in Dynamic Programming
How Memoization is different from Tabulation?
| Memoization | Tabulation | |
|---|---|---|
| State | State transition relation is easy to think. | State transition relation is difficult to think. |
| Code | Code is easy and less complicated. | Code gets complicated when a lot of conditions are required. |
| Speed | Slow due to many **recursive calls and return statements. | Fast, as we directly access previous states from the table. |
| Subproblem solving | If some subproblems in the subproblem space need not be solved at all, the **memoized solution has the advantage of solving only those subproblems that are definitely required. | If all subproblems must be solved at least once, a bottom-up dynamic programming algorithm usually outperforms a top-down memoized algorithm by a constant factor. |
| Table Entries | Unlike the Tabulated version, all entries of the lookup table are not necessarily filled in Memoized version. The table is filled on demand. | In the Tabulated version, starting from the first entry, all entries are filled one by one |
Please refer to Tabulation vs Memoization for better understanding.
Coding Practice Problems on Memoization
| Question | Article | Practice |
|---|---|---|
| Count ways to reach the n’th stair | View | Solve |
| Word Break Problem | DP-32 | View | Solve |
| Program for Fibonacci numbers | View | Solve |
| nth Catalan Number | View | Solve |
| Gold Mine Problem | View | Solve |
| Subset Sum Problem | View | Solve |
| Cutting a Rod | View | Solve |
| Min Cost Path | View | Solve |
| Minimum number of jumps to reach end | View | Solve |
| Longest Palindromic Substring | Set 1 | View | Solve |
| Longest Repeating Subsequence | View | Solve |
| Count ways to reach the nth stair using step 1, 2 or 3 | View | Solve |
| Count of different ways to express n as the sum of 1, 3 and 4 | View | Solve |
| Count number of ways to cover a distance | View | Solve |
| Count of arrays having consecutive element with different values | View | Solve |
| Largest Sum Contiguous Subarray | View | Solve |
| Smallest sum contiguous subarray | View | Solve |
| Unique paths in a Grid with Obstacles | View | Solve |
| Different ways to sum n using numbers greater than or equal to m | View | Solve |
Conclusion
Memoization is a programming concept and can be applied to any programming language. Its absolute goal is to optimize the program. Usually, this problem is seen when programs perform heavy computations. This technique cache all the previous result that is computed so that it will not have to recalculate for the same problem.