ENSO and cholera: A nonstationary link related to climate change? (original) (raw)
Abstract
We present here quantitative evidence for an increased role of interannual climate variability on the temporal dynamics of an infectious disease. The evidence is based on time-series analyses of the relationship between El Niño/Southern Oscillation (ENSO) and cholera prevalence in Bangladesh (formerly Bengal) during two different time periods. A strong and consistent signature of ENSO is apparent in the last two decades (1980–2001), while it is weaker and eventually uncorrelated during the first parts of the last century (1893–1920 and 1920–1940, respectively). Concomitant with these changes, the Southern Oscillation Index (SOI) undergoes shifts in its frequency spectrum. These changes include an intensification of the approximately 4-yr cycle during the recent interval as a response to the well documented Pacific basin regime shift of 1976. This change in remote ENSO modulation alone can only partially serve to substantiate the differences observed in cholera. Regional or basin-wide changes possibly linked to global warming must be invoked that seem to facilitate ENSO transmission. For the recent cholera series and during specific time intervals corresponding to local maxima in ENSO, this climate phenomenon accounts for over 70% of disease variance. This strong association is discontinuous in time and can only be captured with a technique designed to isolate transient couplings.
A main issue at the center of the current debate on climate change is the impact that any anthropogenic-induced changes will have on human society (1, 2). Of considerable importance among these impacts are those affecting human health, particularly the spread and intensification of water-born (1, 3–7) and vector-born diseases (1, 8, 9). A central difficulty that precludes quantitative assessment of these impacts arises from the lack of studies comparing past and present dynamics of infectious diseases over sufficiently long time periods relevant to climate change. For endemic diseases with a long history, such as cholera in Bangladesh, the existence of historical records and on-going surveillance programs make such a comparison possible. Studies of climate and disease so far have been limited to two main areas: the exploration of links between temporal patterns of disease and the interannual variability of climate, mainly El Niño/Southern Oscillation (ENSO; e.g., ref. 7), and the building of scenarios for the geographical spread of disease with climate change (e.g., refs. 10 and 11). The former addresses only interannual variability; it does not address long-term change. Thus, for endemic diseases such as cholera, one key question has been overlooked. Has the interannual variability of climate become a stronger driver of disease dynamics in recent decades? Currently, there is considerable interest in the consequences of climate change for the interannual variability of climate itself, particularly for ENSO and associated phenomena (12). In this context, the question of a nonstationary link between climate variability and disease dynamics is central to address the effect of climate change.
We provide here evidence for a change in the association of cholera dynamics and ENSO from the first to the last decades of the 20th century. Previous results support a role of ENSO in cholera dynamics in the past 2 decades in the Indian subcontinent, specifically in Bangladesh (7). Historical data for cholera in former Bengal allow us to compare here past and present patterns of disease prevalence and their relationship to climate variability.
Methods and Data
We will use a variety of techniques to demonstrate a strong and consistent association between cholera levels and ENSO in the past 2 decades, which is initially more irregular in the earlier time period and then absent from the historical record. Singular spectrum analysis (SSA; Appendix) is first applied to isolate the main interannual variability in the data. To determine the frequencies present in these interannual patterns, the power spectra of the reconstructed time series are obtained with the maximum entropy method (MEM; ref. 13). Comparison of the dominant frequencies supports an intensification of the role of climate variability from past to present. The original time series are then analyzed to quantify the strength of the association between cholera and ENSO with a method specifically developed to identify transient couplings (ref. 14; Appendix). The strong recent coupling is discontinuous in time, occurring during intervals of local maxima in ENSO. Results are interpreted in light of the reported variation in regional climate in the past decades.
The data for the historical period (hereafter referred to as past) consist of monthly cholera mortality for the district of Dhaka in former Bengal from 1893 to 1940 (15, 16). The mortality data were normalized to a constant fraction of the population (mortality per thousand) based on population censuses for Bengal available every 10 yr (from 1891 to 1941), with population numbers between censuses interpolated linearly. The data for the recent period (hereafter referred as present) were obtained by the ICDDR (International Center for Diarrhoeal Disease Research, Bangladesh) in Dhaka from a systematic subsample of all patients visiting their hospital. The selection of patients for cholera testing, which includes both inpatients and outpatients, is carried out randomly and not on the basis of diarrhoeal symptoms. The percentage tested that is infected with cholera is reported monthly from 1980–2001 (see Fig. 1 and Appendix). The Southern Oscillation Index (SOI) series covers the same time intervals as for cholera (17, 18).
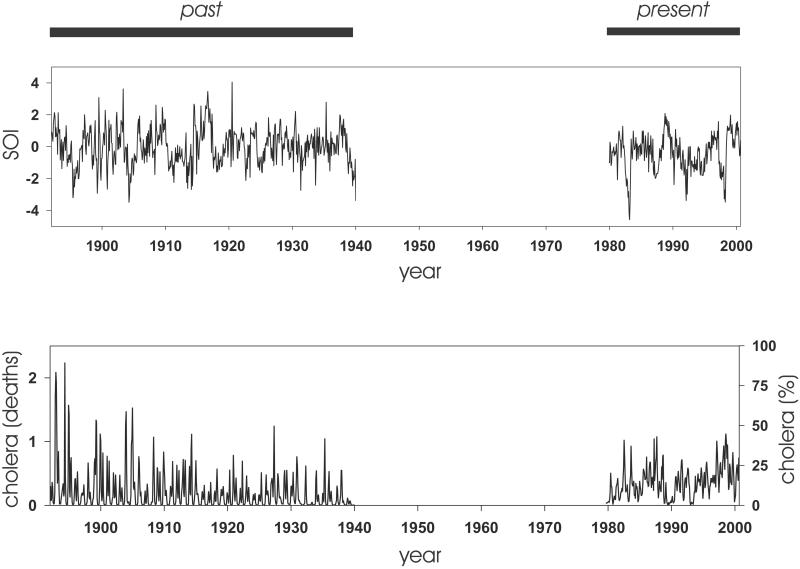
Figure 1.
(Upper) Standardized SOI series for the past (1893–1940) and present (1980–2001) periods. Values between 1940 and 1980 are not shown in accordance with the period with no cholera data. (Lower) Total cholera deaths (mortality) in Dhaka (Bangladesh) for the historical period 1893–1940, and percentage of cholera cases (cholera morbidity) in the same region for the present period (1980–2001). Scale at left is in mortality per 1,000 individuals and scale at right refers to percentages (see Methods and Data).
Results
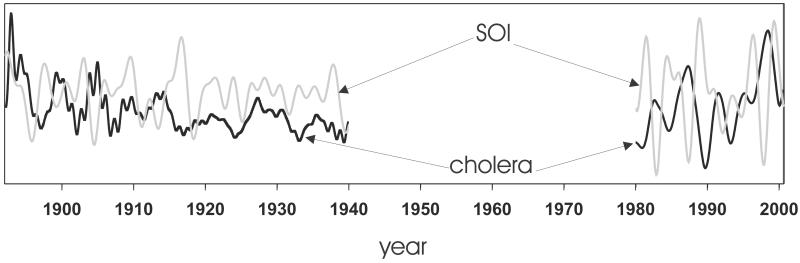
SSA was applied to each of the four time series with seasonality removed to isolate the dominant interannual variation in the dynamics (19–21). Fig. 2 shows the temporal evolution of the resulting reconstructions (RCs) corresponding to the first four eigenvalues. A more prominent quasiquadrennial cycle (a period of between 4 and 5 yr) seems to dominate the present portion of both records (Fig. 2; and see also Fig. 4) with a striking correspondence of maxima of cholera to minima of SOI. The past reconstructed dynamics for both cholera and ENSO seem to change in amplitude and in dominant frequencies around 1915–20. Concomitant cycles of opposite phase are not apparent in the past, particularly after 1915–1920 with a few exceptions in the earlier part of the record around 1899 and 1905, and perhaps also 1912. Examination of the variance spectrum for the SSA decomposition and of the frequency spectrum for the reconstructed time series allow us to examine these observations quantitatively.
Figure 2.
Reconstructions of the first cluster of eigenvalues detected by SSA (refs. 19 and 20, and Appendix) of the cholera and SOI series in Fig. 1. The reconstruction of principal components (PCs) 1 to 4 for cholera is plotted in black, whereas that of PCs 1 to 4 for SOI is shown in gray. In all cases, a window length of 60 months was used for the reconstructions to capture periods of ≈2 and 4 yr (the quasibiennial and quasiquadrennial components, respectively) in both ENSO and cholera.
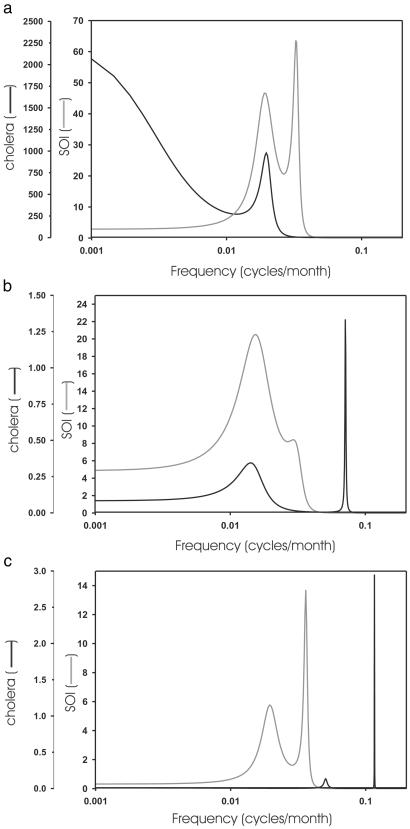
Figure 4.
Frequency spectra computed for the reconstructed time series of cholera and SOI of Fig. 2, for the present (a) and past divided into two periods, 1893–1920 (b) and 1920–1940 (c). The frequency spectra were obtained with the MEM. During the last 2 decades, a quasiquadrennial cycle is present for both ENSO and cholera which closely matches in frequency (a). This correspondence is also seen for the first part of the historical record (b: main period at 6.5 yr) but disappears with no clear dominant frequency in the interannual variability of cholera in the later part (c). The spectrum of SOI for the present shows a more important contribution of the 4–5 yr range. This part of the spectrum weakens around 1920 (c). (For consistency, results were crosschecked with those from the multitaper method spectrum analysis).
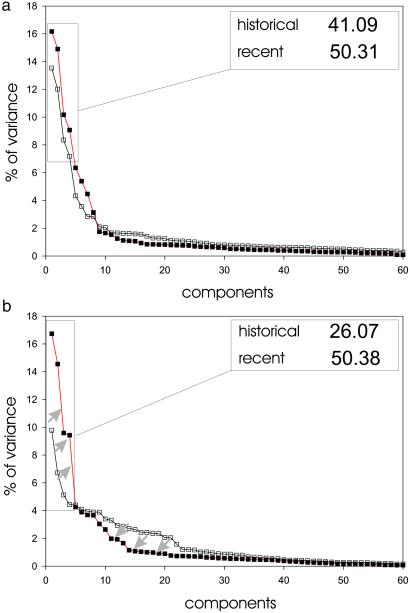
Comparison of the SSA variance spectra between past and present shows a substantial increase in the relative weight of the four eigenvalues accounting for the dominant interannual variability of cholera (from 26% to 50%, Fig. 3b). There is also an increase for SOI in the contribution of the dominant eigenvalues, although it is a more moderate one (from 41% to 50%, Fig. 3a). As typically observed for nonlinear signals, three different portions in the variance spectrum can be consistently isolated: (i) a group of dominant and significant eigenvalues; (ii) an intermediate slope; and finally (iii) a noise floor (Fig. 3b). These regions are interpreted as corresponding to (i) the deterministic variability generated by internal processes and/or extrinsic forcing, which contains the main oscillatory components; (ii) the nonlinear interactions between the former; and finally (iii) the unpredictable part of the signal undistinguishable from noise (22). For cholera, there is both a substantial increase in the relative importance of the first part of the spectrum as well as a noticeable decrease in the contribution of the middle region, from past to present (Fig. 3b). Based on the comparison below of the dominant frequencies present in the reconstructed time series, we interpret these changes as the result of a more prominent role of climate forcing by ENSO in the present.
Figure 3.
Variance spectra for the series in Fig. 1. (a) SOI. (b) Cholera. White and black squares refer to past and present intervals, respectively. The relative variance accounted for by the four reconstructed components of Fig. 2 is shown separately for the historical and present periods in Inset. Gray arrows in b indicate the changes occurring in the different portions of the spectra. For all analyses, a window length of 60 months was selected to be able to isolate the typical temporal scales of El Niño.
Fig. 4 shows the frequency spectra for the reconstructed time series. Dominant frequencies correspond to peaks in these spectra. For both variables, the frequency spectra show changes over time but demonstrate that the interannual variability of present cholera, a cycle of ≈4- to 5-yr periodicity, matches clearly the dominant frequency of SOI (Fig. 4a). For the past, the data were analyzed both for the whole time series and for the first and second parts separately to examine possible changes before and after 1915–1920. Results show that, for the first part of the historical record, a peak of ≈6.5 yr is present for both cholera and SOI (Fig. 4b). This correspondence breaks down, however, when for SOI, the contribution of this component weakens in the second part of the record (Fig. 4c). These changes in the frequency spectrum of SOI are consistent with those described for ENSO in the literature (23). These results support a nonstationary relationship between cholera in Dhaka and ENSO, with climate variability acting as a strong driver of disease dynamics in recent times.
To examine this possibility further, we analyzed the original data with a method that specifically quantifies the strength of the association between variables and does so locally in time. This property of scale-dependent correlation (SDC) analysis (14) is important because reported linear correlations between disease dynamics and climate variability, which average over the whole record, are typically low (7). Two possible reasons arise: either climatic variables are weak drivers and the dynamics of disease are influenced by myriad other factors, or they are strong drivers but in a nonlinear fashion acting only during specific intervals of time corresponding to extreme events. The latter implies a discontinuous association between variables that is not properly addressed by standard statistical techniques but is detected by SDC analysis, a time series method specifically developed to isolate transient signals (14).
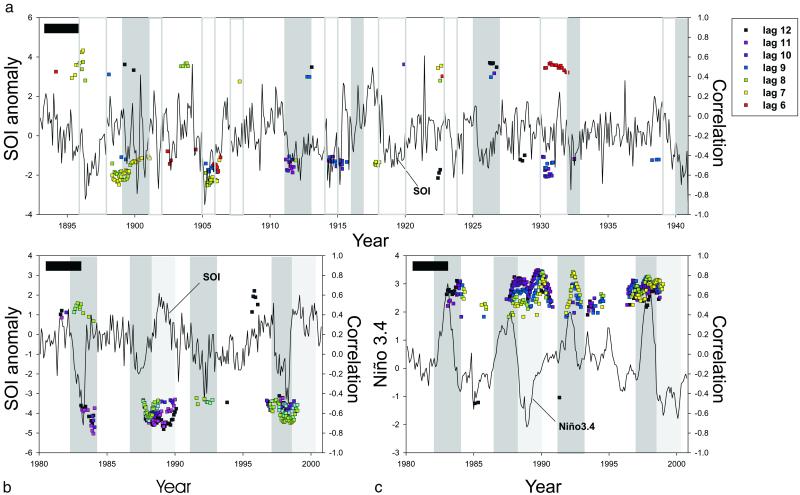
Fig. 5 shows the results of the analysis applied to past and present intervals. These results show again sharp contrasts between past and present, with evidence for a stronger and more consistent association between variables in recent times. SDC analysis essentially obtains correlation values locally in time by computing and determining the significance of correlation coefficients in windows of a given size along the two records and for a given time lag between the variables (14). In Fig. 5, only local correlation values significant at the 0.01 level are reported and shown with respect to the position of the time window for the ENSO index. For the historical records, the pattern of significant correlations is sparse and highly irregular, with few correlations significant at P < 0.01. The distributions of these correlations in time show no consistent regular aggregation with respect to SOI maxima or minima. Only in the first part of the historical data, small clusters of negative correlations barely comparable to present ones are apparent for two of these clusters and weaker otherwise (Fig. 5a). In the present, significant and typically higher correlations (often as high as 0.9, with a maximum for the La Niña of 1988–89) are obtained for the recent records, but they are discontinuous in time (Fig. 5 b and c). The times of such high correlations cluster and coincide with both warm and cold phases of ENSO, as shown by superimposing on the figure an alternating banded pattern for the reported El Niño and La Niña episodes identified since 1980. A delay ranging from +7 to +12 months between the peaks (whether positive or negative) in ENSO and the maximum correlation with cholera is apparent from Fig. 5 b and c). In addition, all groups of correlations are of the same sign, negative for SOI (Fig. 5b) and positive for Niño 3.4 (Fig. 5c), indicating an increase/decrease in cholera after warm/cold ENSO events, respectively. In the present, however, no association persists between cholera and ENSO for intervals among peaks. The coupling between cholera and ENSO is, therefore, strong but transient, occurring only during specific intervals of time corresponding to extreme events (Fig. 5 b and c). This on–off relationship may result from a threshold above which the influence of climate on disease dynamics is activated. This finding explains the low and uninformative value of the linear correlation between variables that is obtained by averaging over periods of coupling and decoupling (a maximum of r = +0.29 at a lag of 10 months for the present record).
Figure 5.
Results of the SDC analysis (14) for both the historical or past period (a) and the present interval (b and c). SDC analysis computes all possible correlations between fragments of a given size for all locations in the two series. Several window sizes were inspected in intermediate plots (not shown) for each analysis, namely S = 200, S = 100, and S = 25. The window S = 25 was chosen as a scale that produces the highest local correlations. This fragment size appears as a black bar in the top-left corner of each graph. Significant correlations are represented by points anchored in the central value of the fragment size (S) that has been used to calculate correlations. In this figure, the ENSO time series (SOI or Niño 3.4) is used as the reference data set to display the location of significant correlations. The colors of the dots correspond to different time lags for the location of the respective fragment in the cholera data set, with cholera lagging SOI in b or Niño 3.4 in c. Significance levels are P < 0.01 for all points in the graph, and P < 0.00001 for the overall SDC pattern (14). Boxes refer to strong–very strong El Niño (dark boxes), strong–very strong La Niña (light-gray boxes), and moderate ENSO episodes (white boxes). Episodes were classified according to standardized terminology, both for the historical ENSO period (39) and for the recent interval (40). The analysis identifies isolated episodes of covariation and quantifies the corresponding local contribution to the overall variance. Local correlations in the four EN episodes attain values up to a maximum of r(−8 months)xy = 0.84 (P < 0.0001) in the EN of 1991. The highest values for the La Niña of 1988 are r(−11 months)xy = 0.86 (P < 0.0001). Thus, ENSO accounts for over 70% of total variability in the recent cholera series during transient intervals of association. These intervals overlap with the timing of the highest cholera cases. Outside these intervals, the two dynamics decouple, with correlation values close to zero. Comparison among results obtained with both SOI and Niño 3.4 indicate the superior utility of oceanic conditions in the tropical Pacific as remote predictors for cholera (c). Values attained are slightly higher for Niño 3.4, and the clusters associated to each episode are formed by many more correlations than when calculated with the SOI. Because of the quality of historical SST records in the Niño region, only sea-level pressures (or SOI) were considered for that period. Correlations with Niño 3.4 are able to capture peaks in cholera for the complex 1991–1994 episode, an episode otherwise insensitive to SOI analyses. An ENSO signature clearly dominates the recent cholera series, whereas it is more inconsistent and then largely absent from first and second parts of the historical record, respectively. (See Appendix and ref. 14 for further details on the method).
Discussion
An intensification of the role of ENSO in cholera dynamics must be interpreted in light of the known changes of ENSO itself in the past decades and ultimately tied to variation in regional climate to provide a mechanistic explanation. The ENSO system is the primary driver of interannual variability in global climate, but its long-term behavior is poorly understood. Instrumental observations reveal a shift in 1976, unique in this past century, toward an intensified hydrologic cycle under doubled CO2 scenarios (24) and warmer and wetter conditions in the tropical Pacific, with widespread climatic and ecological consequences. It is further recognized that the recent changes in the influence of El Niño in the subtropics are closely related to this shift in ENSO, with a tendency toward warmer events since the late 1970s and the appearance of occasional episodes of prolonged warm anomalies such as the one in the early 1990s. From the 1980s onwards, there has been a noticeable increase in the variance of ENSO, with a strong amplification in its quasiquadrennial component (Fig. 2) relative to other periods in the record for which the quasibiennial component is dominant (25).
At a regional level, it has been documented that changes in the ENSO quasiquadrennial component of the last 3 decades occur in coincidence with a southeastward shift in the Walker circulation anomalies (26). This period also coincides with record high global mean temperatures (27). From both observations and model simulations, these changes in ENSO are also qualitatively consistent with those expected from increased greenhouse gases in the atmosphere (28), although this subject remains controversial (29–31). Resulting conditions have favored through the local Hadley cell a reduced subsidence over the Indian region and an increase in surface air temperature (SAT; refs. 25 and 32). An additional increase in SAT in Eurasia linked to the global warming trend seems also to contribute to a much greater warming of the Indian subcontinent compared with the adjacent tropical oceans (33). Both ENSO and these global warming effects have contributed to winter (December, January, and February) temperature increases in the Indian region, of between 2 and 3° C in 1981–1997 with regard to 1871–1980 (26). Maxima in temperatures centered over the Tibetan Plateau and more inland areas also could strongly affect the snowpack dynamics in the Himalayas, ultimately altering its interannual retreat–recovery dynamics and affecting the monsoonal flow and the river flood discharge over the lowlands in coastal Bangladesh.
Warming over land in the Indian subcontinent may have noticeable effects on the temperature of water bodies that serve as an environmental habitat and as a vehicle of transmission for the bacterium. Water temperature is known to affect the proliferation of the bacterium (34). Regional correlation maps have shown a significant association of temperature with the recent cholera data for Dhaka (7). Enhanced warming also can affect disease transmission by changing human behavior, with a possible increase in the contact with contaminated water sources under warm conditions immediately before and during the spring, when the first seasonal peak in cholera is typically observed in Dhaka. The effect of more extreme ENSO and global warming conditions of drought and flood, which remain to be examined but are consistent with future global and regional scenarios (35), also might impact sanitation conditions critical to cholera transmission.
Individually or in combination, any of these factors could now underlie a more effective role of climate variability in the dynamics of cholera. A higher mean in the climatology also could facilitate the more frequent attainment of a threshold that, when surpassed, activates an identifiable effect in cholera.
Most observational and modeling evidence points so far to an increase in both the amplitude and variability of ENSO in the years to come under a global warming scenario (36) or, alternatively, as the result of natural variability on decadal or longer time scales (37). The consequences for infectious diseases are only now beginning to be foreseen. Our results support a sustained, and possibly intensified, future role of ENSO in the interannual variability of cholera.
Supplementary Material
Supporting Figure
Acknowledgments
We thank M. A. Rodríguez-Arias and J. A. Morguí for useful discussions, M. J. Bouma for the historical data, and A. P. Dobson for comments on an earlier version of the manuscript. This work was supported by a National Oceanic and Atmospheric Administration grant (Joint Program on Climate Variability and Human Health, with Electric Power Research Institute–National Science Foundation–Environmental Protection Agency–National Aeronautics and Space Administration) and a James S. McDonnell Foundation Centennial fellowship (to M.P.) and by Ramon y Cajal Contract MCYT (to X.R.).
Abbreviations
ENSO
El Niño/Southern Oscillation
SOI
Southern Oscillation Index
SSA
singular spectrum analysis
SDC
scale-dependent correlation
Methods and Data
SSA.
SSA provides a decomposition of the signal into its significant and noisy parts (19–21). Specifically, SSA decomposes the dynamics of a time series into a (nonlinear) trend, oscillatory components, including those with anharmonic shapes, and noise. Based on principal component analysis, the method yields a set of eigenvalues and eigenvectors from a symmetric covariance matrix. This matrix contains in column j and row i the covariance of the data at lag i-j. It is obtained by first augmenting the time series of interest, say n(t), into a multivariate time series N(t) = [n(t + 1), n(t + 2), … , n(t + M)] where M is called the window length or embedding dimension. The eigenvalues of the covariance matrix quantify the variance associated with each eigenvector and are plotted in decreasing order in the SSA variance spectrum (Fig. 3). The corresponding eigenvectors are known as empirical orthogonal functions or EOFs. Projection of the signal onto the EOFs gives the principal components (PCs). To reconstruct the time series, the EOFs associated with the first group of significant eigenvalues are chosen, and the associated PCs are combined. The reconstructions (RCs) preserve the phase of the time series and produce no loss of information, in the sense that the sum of all individual reconstructed components gives the original time series. SSA has been shown to be well suited for the analysis of short and noisy time series from nonlinear systems (21).
Here, several realizations of SSA were performed for each time series, with varying window length M, to check for consistency in the decomposition obtained. The shape of the eigenspectrum is roughly independent of M in the four cases (for both cholera and SOI in the past and present intervals), except for historical cholera, which presents slight variations because of its nonstationary character. Monte Carlo tests for red and white noise were used in all cases to assess the significance of the components analyzed with respect to noise realizations (38). The two empirical orthogonal functions (EOFs) in each one of the two leading pairs (EOFs 1 and 2 and EOFs 3 and 4) are in phase quadrature and correspond to a pair of eigenvalues that are approximately equal and have overlapping error bars. Such pairs provide evidence for oscillatory components (32).
SDC Analysis.
In SDC analysis (14), correlations are calculated among fragments of a given size (S = length of fragment or window) between the two series and at all locations in both series. The analysis is repeated for different window sizes to identify the intermediate spatial scale that yields the highest correlation values. Local correlations in SDC approach the values of the traditional linear-lag correlation when fragments are comparable in length to the whole series. As S decreases, local patches of higher correlation values typically develop, identifying intervals of stronger association. As S drops below the temporal scale of coupling, local correlations decrease and the patches fragment into random patterns. For a given window size, the significance of specific correlation values between two fragments is evaluated with a randomization test. Surrogate series (random rearrangements of the original data) are first produced by random rearrangements of the original data. SDC uses both an exact randomization procedure, in which all possible rearrangements without repetition are enumerated, and a random sampling of all these possible rearrangements. Specifically, for a given number of data points s, if the required number of permutations (m) is larger than the possible number of surrogates (m > s!), SDC generates all of the rearrangements; otherwise, it switches to a sampled randomization test. The null hypothesis of the test states that the observed correlation between two fragments at a given scale is due to chance alone (HO: rO = 0). Under these conditions, any correlation calculated after a random rearrangement of the elements of one of the segments will be an expected result of HO. SDC performs m random permutations inside the fragments of the first series (_X_[_i,i+s_]) and then correlates each rearranged segment with the second series (_Y_[_j,j+s_]) to yield the reference distribution under the null hypothesis. This distribution is then used to calculate the probability of the observed correlation, P(rO). Because we are interested in all of the significant correlations, SDC performs different one-tailed tests depending on the sign. When rO is significant [with P(rO) < α for the selected significance threshold α], SDC adds a dot in the graph (e.g., Fig. 5). Significance is also evaluated for the overall pattern of correlations for all possible locations of fragments in a two-dimensional graph whose pattern is tested against the expectation of a binomial-based null model. In this graph, each point represents the location and intensity of a significant correlation above a threshold value.
Cholera Data.
Cholera percentages are used, rather than cholera cases, for the recent period because in the surveillance program, the total number of people tested varied over time (as this number is a fixed percentage of the population visiting the clinic). Thus, percent cases is a better surrogate for real cholera cases in the population at large. However, cholera cases and percent cholera cases are highly correlated (rxy = +0.93, P < 0.001; Fig. 6, which is published as supporting information on the PNAS web site, www.pnas.org), and the choice of variable does not alter our results. For the past, cholera mortality provides another surrogate for cholera cases, as a large fraction of infected persons died of the disease (16). Our analyses and conclusions are based largely on the temporal patterns of variation (frequencies and timing of events) and covariation within time periods. They do not rely on the direct comparison of absolute values and variances of the cholera data. This observation justifies the use of two different measurements (deaths and percent cases) for cholera levels.
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
See commentary on page 12506.
References
- 1.Watson R T, Zinyowera M C, Moss R H. IPCC Special Report on The Regional Impacts of Climate Change: An Assessment of Vulnerability. Cambridge, U.K.: Cambridge Univ. Press; 1998. [Google Scholar]
- 2.Huq S S. Science. 2001;294:1617. doi: 10.1126/science.294.5547.1617. [DOI] [PubMed] [Google Scholar]
- 3.Colwell R R. Science. 1996;274:2025–2031. doi: 10.1126/science.274.5295.2025. [DOI] [PubMed] [Google Scholar]
- 4.World Health Organization. Regional Health Report 1996. Geneva: W.H.O.; 1996. [Google Scholar]
- 5.Brandling-Bennett A D, Pinheiro F. Emerging Infectious Diseases. 1996;2:59–61. doi: 10.3201/eid0201.960109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.McCarthy M. Lancet. 2001;357:1183. doi: 10.1016/S0140-6736(00)04388-9. [DOI] [PubMed] [Google Scholar]
- 7.Pascual M, Rodó X, Ellner S, Colwell R, Bouma M. Science. 2000;289:1766–1769. doi: 10.1126/science.289.5485.1766. [DOI] [PubMed] [Google Scholar]
- 8.Martens W J, Niessen L W, Rotmans J, Jetten T H, McMichael A. Environ Health Perspect. 1995;103:458–464. doi: 10.1289/ehp.95103458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.McMichael A, Haines A, Slooff R, Kovats S, editors. World Health Organization. Climate Change and Human Health. Geneva: W.H.O.; 1996. [Google Scholar]
- 10.Jetten T H, Focks D A. Am J Trop Med Hyg. 1997;57:285–297. doi: 10.4269/ajtmh.1997.57.285. [DOI] [PubMed] [Google Scholar]
- 11.Martens W J, Jetten T H, Rotmans J, Niessen L W. Global Environ Change. 1995;5:195–209. doi: 10.1289/ehp.95103458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hartmann D L. Science. 2002;295:811–812. doi: 10.1126/science.1068447. [DOI] [PubMed] [Google Scholar]
- 13.Childers D G, editor. Modern Spectrum Analysis. New York: IEEE; 1978. [Google Scholar]
- 14.Rodó X. Clim Dyn. 2001;18:203–217. [Google Scholar]
- Sanitary Commissioner for Bengal Reports (yearly) Bengal Public Health Reports, 1891–1942 (Bengal Secretariat, Calcutta and Bengal Government, Alipore).
- 16.Bouma M J, Pascual M. Hydrobiologia. 2001;460:147–156. [Google Scholar]
- 17.Ropelewski C F, Jones P D. Mon Wea Rev. 1987;115:2161–2165. [Google Scholar]
- 18.Allan R J, Nicholls N, Jones P D, Butterworth I J. J Clim. 1991;4:743–749. [Google Scholar]
- 19.Broomhead D S, King G. Physica D. 1986;20:217–236. [Google Scholar]
- 20.Vautard R, Ghil M. Physica D. 1989;35:395–424. [Google Scholar]
- 21.Vautard R, Yiou P, Ghil M. Physica D. 1992;58:95–126. [Google Scholar]
- 22.Yiou P, Ghil M, Jouzel J, Paillard D, Vautard R. Clim Dyn. 1994;9:371–389. [Google Scholar]
- 23.Torrence C, Compo G P. Bull Am Met Soc. 1998;79:61–78. [Google Scholar]
- 24.Graham N E. Simulation of Recent Global Temperature Trends. Scripps Institute for Oceanography; 1994. , No. 9425. [DOI] [PubMed] [Google Scholar]
- 25.Webster P J, Magana V O, Palmer T N, Shukla J, Tomas R A, Yanai M, Yasunari T. J Geophys Res. 1998;103:14451–14510. [Google Scholar]
- 26.Kumar K K, Rajagopalan B, Cane M A. Science. 1999;284:2156–2159. doi: 10.1126/science.284.5423.2156. [DOI] [PubMed] [Google Scholar]
- 27.Shrestha A B, Wake C, Dibb J, Mayewski P. Int J Clim. 2000;20:317–327. [Google Scholar]
- 28.Dai A, Trenberth K, Karl T. Geophys Res Lett. 1998;25:3367–3370. [Google Scholar]
- 29.Urban F E, Cole J, Overpeck J. Nature (London) 2000;407:989–993. doi: 10.1038/35039597. [DOI] [PubMed] [Google Scholar]
- 30.Trenberth K, Hoar T. Geophys Res Lett. 1996;23:57–60. [Google Scholar]
- 31.Knutson T R, Manabe S. J Clim. 1998;11:2273–2296. [Google Scholar]
- 32.Klein S A, Soden B J, Lau N-C. J Clim. 1999;12:917–932. [Google Scholar]
- 33.Meehl G A, Washington W M. Nature (London) 1996;382:56–60. [Google Scholar]
- 34.Singleton F L, Atwell R W, Jangi M S, Colwell R R. Appl Environ Microbiol. 1984;44:1047–1058. doi: 10.1128/aem.44.5.1047-1058.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Houghton J T, Ding Y, Griggs D J, Noguer M, van der Linden P J, Xiaosu D, editors. Climate Change 2001: The Scientific Basis. Cambridge, U.K.: Cambridge Univ. Press; 2001. [Google Scholar]
- 36.Timmermann A. Nature (London) 1999;398:694–697. [Google Scholar]
- 37.Chen J, Carlson B E, DelGenio A D. Science. 2002;295:838–841. doi: 10.1126/science.1065835. [DOI] [PubMed] [Google Scholar]
- 38.Dettinger M D, Ghil M, Strong C M, Weibel W, Yiou P. EOS Trans Am Geophys Union. 1995;76:12–21. [Google Scholar]
- 39.Quinn W H, Neal V, Mayolo S E. J Geophys Res. 1987;92:14.449–14.461. [Google Scholar]
- 40.Smith C A, Sardeshmukh P. Int J Clim. 2000;20:1543–1557. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Figure