Cellular dynamics extracted from populations of fixed cells reveals a feedback between growth and progression through the cell cycle (original) (raw)
. Author manuscript; available in PMC: 2013 Aug 28.
Published in final edited form as: Nature. 2013 Feb 28;494(7438):480–483. doi: 10.1038/nature11897
Abstract
Biologists have long been concerned about what constrains variation in cell size; yet, progress on this question has been slow and stymied by experimental limitations1. We describe a new method, ergodic rate analysis (ERA), that uses single cell measurements of fixed steady-state populations to accurately infer the rates of molecular events, including rates of cell growth. ERA exploits the fact that the number of cells in a particular state is related to the average transit time through that state2. With this method, one can calculate full time trajectories of any feature that can be labeled fixed cells, for example levels of phospho-proteins or total cellular mass. Using ERA we find evidence for a size-discriminatory process at the G1/S transition that acts to decrease cell-to-cell size variation.
Size is an obvious and distinguishing feature of cells, characteristic of their physiology and pathology. A barrier to studying size control in mammalian cells is the inaccuracy in measuring size, growth rate, and the dynamics of pathways controlling growth and proliferation1. To overcome these obstacles, we developed ergodic rate analysis (ERA), a procedure for extracting dynamics and regulatory relationships from a single image of a population of individual fixed cells. ERA makes use of the fact that, at steady state, the number of cells in any particular molecular state is related to the rate at which cells transit through that state2. Using this method, we calculated the dynamics of cell growth and cell cycle progression and investigated the processes that limit size variation.
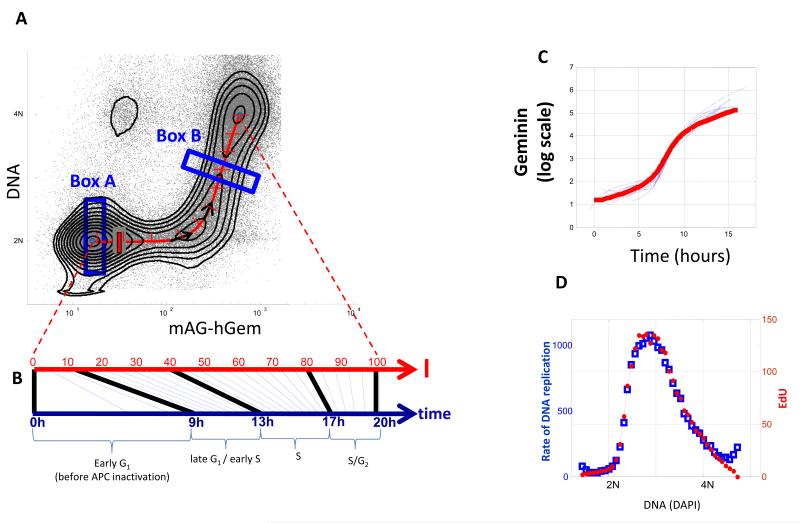
To determine precise cell cycle dynamics from a single image of fixed cells we considered the fact that unsynchronized proliferating cells are often found to be in a quasi-steady state, in which the proportion of cells in each phase of the cell cycle is stable (Fig. 1). We determine cell cycle position by measuring the levels of both DNA and a fluorescent reporter of the Geminin degron (mAG-hGem)3. In the context of the present study, mAG-hGem serves as a marker for activity of anaphase promoting complex (APC). The scatter plot in Fig 1 demonstrates the well-known decrease in APC activity in late G1 (resulting in mAG-hGem accumulation), which is followed by doubling of DNA in S-phase. Reactivation of APC at mitosis results in a sharp fall in mAG-hGem fluorescence followed by cytokinesis where DNA levels drop by one half (Fig. 1). For populations 12 hours post fixation that have not reached confluence, the distribution, f, of cells in the plane defined by these two measurements is independent of the time at which cells were sampled and fixed, as shown in the supplementary material. The existence of a stationary state condition imposes a quantitative relationship between the proportion of cells in different regions of the plot and the rates of molecular events (i.e. changes in DNA and APC activity). For example, in Fig 1, because every cycling cell passes through the labeled regions A and B, the higher cell count in region A must mean that cells traverse this region at slower rates than in region B (see Box 1).
Figure 1.
Dynamic information from static data using ERA. (A) Levels of DNA (DAPI) and Geminin (mAG-hGem) in an unsynchronized, exponential population of HeLa cells. The black contour lines denote the distribution, f, of cells within the DNA/Geminin plane. Also shown is the average cell cycle trajectory, I, (red). The different densities of cells in boxes A and B result from the different rates at which cells traverse those regions. (B) The transformation of the cell cycle axis, I, to a real time axis. For convenience we chose 100 units of I to represent a complete path from the beginning of G1 to the end of G2. Comparison of ERA with direct dynamical measurements (C-D). (C) Accumulation of Geminin (mAG-hGem) was followed in 10 individual live cells by time lapse microscopy (blue lines) and compared to the dynamics of mAG-hGem calculated from fixed cells using ERA (red). (D) DNA replication rate was measured by exposing cells to a 20 min. pulse of EdU (5-ethynyl-2′-deoxyuridine, Invitrogen) prior to fixation. Average levels of EdU fluorescence per cell (indicating rate of DNA replication) are plotted (blue) as a function of DAPI, giving a measure of the mean rate of DNA replication as a function of passage through S. For comparison, ERA was used to calculate DNA replication rates directly from fixed cells not treated with EdU (red).
Box 1. The ERA Balance Equation.
ERA rests on the fact that at steady state the difference, - _Nt_N~g(fv), between the rates at which cells enter and leave any given molecular state must be balanced by the increase in cell count in that state. Nt is the total number of cells in the population at time t, f is the proportion of cells in the given state ( indicated by the black contour lines in Fig 1), and v is the rate at which cells pass through that state. Since f does not change with time, the number of cells at any given state as a function of time is fNt = fN0eαt. These considerations result in a simple balance equation:
where α is the proportion of cells dividing per unit time and B is a term accounting for cell division (see Supplementary material). As we will show, Eq. 1 can be used to derive accurate time profiles from a single measurement on a population of fixed cells. If more parameters are measured, the dimensionality of the plot increases but the analyses remain the same. Eq. 1 is free of any mechanistic assumptions or free variables and is grounded only on a basic conservation principle akin to conservation of mass. Eq. 1 and its implementations throughout this study are based on two main assumptions outlined in detail in the Supplementary material: the first is that the representation axes (which in the present study are DNA and APC activity) appropriately represent both individual and collective cell behavior and the second is that the steady state assumptions described above apply.
Our goal in this study was to use Eq. 1 (Box 1) to determine the growth rate of cells at different points in the cell cycle, in other words to solve for v. To solve Eq. 1 we reduced the number of dimensions from DNA (1st dim) and APC/C activity (2nd dim) to a single dimension, I, representing cell cycle progression over time (see Box 2). While I is not directly measured, it can be calculated from f, which is obtained experimentally (see Supplementary material). Fig 1A shows I (red curve) superimposed on the single cell measurements.
Box 2. Reducing the dimensionality of Equation 1.
Confining Eq. 1 to the cell cycle trajectory, I, and integrating results in an expression (Eq. 2) that relates measured probability density, f, to the rate, ω, of progression through the cell cycle, we have:
where F(1)= O`11f(1)d1. Furthermore, since w(l)° d1dt, we can use results of Eq. 2 to calculate a complete time axis for the dynamics of the measured processes using:
| t(10)=o~1=1o´101wd1 | (Eq. 3) |
|---|
where t(ℓ0) is the time it takes for cell starting at position I=1 (G1) to reach position I0 on the cell cycle axis, I. As shown in Fig 1, Equations 1-3 transform a single, non-temporal, measurement on fixed cells into temporal trajectories represented on time axis, t. Fig 1B shows the non-linear transformation (the ERA transform) of a path, I, defined by molecular events, onto a time axis. We conveniently chose 100 units of I to represent a complete path from G1 to G2. We do not include M (metaphase) in this analysis since the number of cells in M is very small. Real time enters this calculation through the doubling time of the population, τ=log(2)α. For solutions of ERA in more than 2 dimensions see Supplementary material.
Fig. 1C compares mAG-hGem dynamics of live cells obtained from time lapse microscopy to dynamics of fixed cells calculated by ERA. There is near perfect agreement. To further demonstrate the utility of ERA, we compared the rate of DNA replication obtained by labeling live cells with EdU to the rate of DNA replication obtained by ERA of DAPI stain intensity in fixed cells (Fig. 1D). As with the previous example, we obtained a striking overlap between the measurements. Both examples demonstrate that ERA calculations can resolve dynamics on the order of minutes.
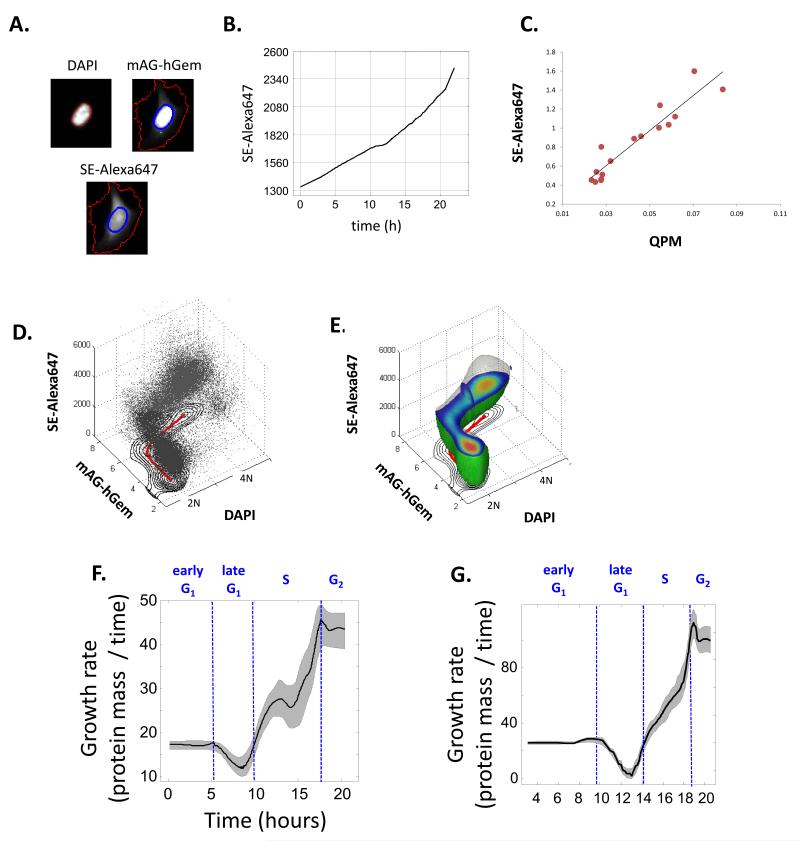
To characterize cell growth dynamics during the cell cycle we quantified the protein mass of individual cells by measuring the total fluorescence intensity from cells stained with a succinimidyl ester dye (SE-A647), which covalently reacts with lysyl groups. This is a good measure of protein mass4 and correlates well with physical measurements of dry mass by quantitative phase microscopy (QPM), whose accuracy is better than 1%5 (Fig. 2C). From these measurements, we assembled a 3-dimensional single-cell dataset simultaneously reporting cell size and cell cycle stage for millions of fixed cells (Fig 2 A,D,E). As expected, our data demonstrates an approximate doubling in protein fluorescence in a single cell cycle (Figure 2B).
Figure 2.
Calculation of growth as a function of cell cycle progression using ERA. (A) Cells were stained and imaged for DNA content (DAPI), the geminin degron (mAG-hGem) and for protein content (succinimidyl ester-Alexa 647 (SE-A647)). (B) Growth during cell cycle progression, computed by ERA. (C) Comparison of SE-A647 fluorescence intensity with quantitative phase microscopy measurements in single cells. Each data point represents a single cell measured for both protein content (SE-647) and phase retardation (QPM). (D) A scatter plot for the levels of DNA (DAPI) Geminin (mAG-hGem) and cell size (SE-A647) in an unsynchronized population of HeLa cells. Also shown is the projection of the 2-dimensional distribution of Geminin and DNA overlaid with I. (E) The 3-dimensional probability distribution from the data shown in 2D (F, G) Growth rate versus time for HeLa (F) and RPE1 (G) calculated by ERA. Confidence intervals are shown as described in Supplementary material.
For four very different cell lines the growth in mass during the cell cycle, as calculated by ERA, produced very similar trajectories that are neither linear nor exponential (Fig 2F, 2G and Supplementary material). The results show that growth rates increase with progression in cell cycle and reach a maximum during G2, consistent with a recent study using QPM6. What is novel is a transient slowdown in protein accumulation rate at the G1/S transition in all cell lines (Fig 2 F-G). Since this slow down occurs for a relatively short time, it is not surprising that it was not detected in previous time course measurements on synchronized populations. Further, by aligning cells using molecular markers of cell cycle progression rather than time, ERA avoids the clouding effects of imperfect synchronization. Plots of growth rate as a function of mass are similar to those obtained recently with the suspended microchannel resonator7 (Supplementary material)
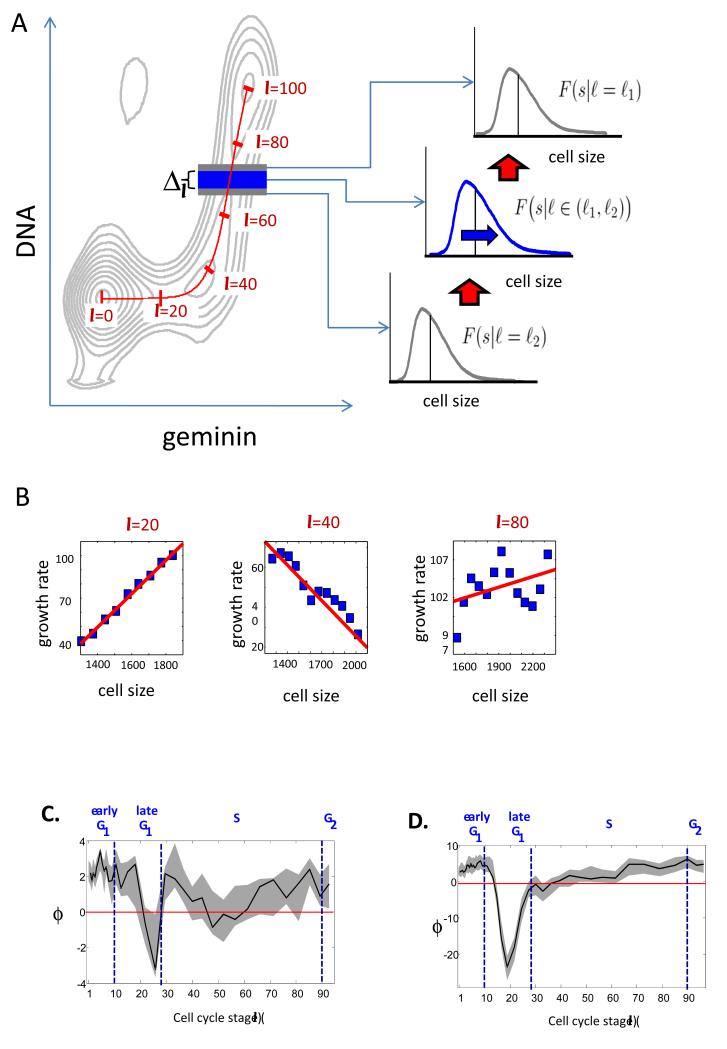
The existence of stable and narrow distributions of cell size suggests cell-autonomous feedbacks controlling size variability. To search for such feedbacks we calculated the joint dependency of growth rate, v, on size, s, and cell cycle position, I (Fig. 3). The size distribution within any interval along the cell cycle path l, Δℓ = (ℓ− w,ℓ+ w), is governed exclusively by (Fig 3): (i) the size distribution of cells entering the interval from the previous cell cycle stage, (ii) the size distribution of cells leaving the interval into a later cell cycle stage, and (iii) cell growth within the interval. Such a formulation allows the construction of a 3-term balance equation relating growth rate to cell size within the interval (see Box 3).
Figure 3.
Rate of cell growth as a function of size and cell cycle. Size discrimination at the G1/S transition. (A) Calculation of growth rate as a function of size for a defined interval, ΔI, on the cell cycle axis, I. To calculate feedback regulation as a function of cell size, the size distributions of cells entering and leaving ΔI are estimated from the sizes of cells on the boundary of ΔI. (B) Plots of growth-rate vs. cell-size at late G1 ( I = 20 ), the G1/S transition ( I = 40) and late S-phase ( I = 80 ). (C,D) The slope, φ, of growth rate vs. cell size plotted as a function of I, for (C), HeLa cells and (D), RPE1 cells. The red horizontal line positioned at φ = 0 is added to emphasize the distinction between positive and negative slopes (positive and negative feedbacks). Blue vertical lines demarcate borders between different stages of cell cycle. Confidence intervals are in gray.
Box 3. Analyzing growth as a function of size.
To obtain the size distributions of cells entering and leaving a given interval we consider the size distributions of cells positioned at the borders of that interval (Fig 3A). These distributions are formally approximated by the conditional probability distributions, F(s | ℓ − w) and F(s | ℓ + w), where F(s | ℓ − w) is the cumulative probability distribution of cell size, s, among cells in the state ℓ − w at the entrance to the interval Δℓ= (ℓ− w,ℓ+ w) (marked red in Fig. 13, Supplementary material), and similarly with F(s| ℓ + w). The width, Δℓ = 2_w_, represents the resolution limit of the calculation. Using this construction we obtain an equation for the rate of cell growth as a function of cell size:
| v(s,Δℓ)=α(2−λA)F(s∣ℓ−w)−(2−λA−λB)F(s0∣ℓ+w)−F(s∣Δℓ)λBf(s∣Δℓ)λB | (Eq. 4) |
|---|
Where F(s,|Δℓ) = F(s | (ℓ −w,ℓ + w)) l is the size distribution within the interval, Δℓ, λA is the fraction of cells occupying all cell cycle stages preceding Δℓ, and λB is the fraction of cells in Δℓ. We use the notation F and f to refer to cumulative and non-cumulative probability distributions, respectively. To further evaluate how the growth-rate/cell-size dependency relates to cell cycle rogression, we translate along the cell cycle axis and repeatedly solve Eq. 4 for all points on I.
Fig 3B plots how growth rate, v, depends on cell size, s, at three different points in the cell cycle; late G1 (I=20), the G1/S transition (I=40) and late S-phase (I=80). A surprising result of this analysis is the shift to a negative slope of growth rate versus cell size for cells around the G1/S transition (see slope for I=40). This negative slope is surprising as it implies that at this point small cells have higher growth rates than larger cells. This cell-size dependent growth rate implies a negative feedback linking growth rate to cell size, effectively constraining cell-to-cell size variability in the population.
Fig. 3A & 3D shows the slope, φ, of the growth rate vs. cell size as a function of the cell cycle progression axis, I. A positive φ implies that larger cells have higher growth rates than smaller cells, while negative φ implies the opposite; φ =0 indicates that growth is independent of cell size. Calculating φ for four different cell lines (Fig 3A, 3D and Supplementary material) yields feedback spectra that consistently acquire negative values at the G1/S transition. The strict interpretation that cell size negatively feeds back on growth rate at G1/S depends on the assumption that progression along I is independent of cell size (see Supplementary material). This is not the only possibility. An alternative interpretation is that size variation is limited not by repressing the growth rate of large cells but by inhibiting the rate at which small cells progress along the cell cycle. Whichever of these interpretations is correct, Eq. 4 identifies fingerprints of a cell-size discriminatory process, occurring at the G1/S transition, that distinguishes small and large cells and results in an increase in the homogeneity of cell size in the proliferating population. These results support very early findings suggesting cell size regulation at the G1/S transition8.
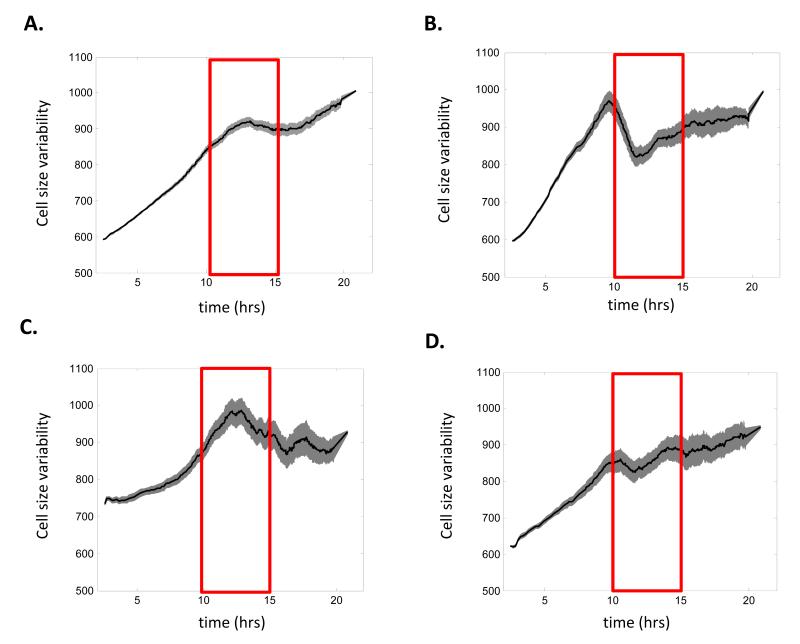
To test further whether growth at G1/S is different for large and small cells, we treated HeLa cells for one hour with a proteasome inhibitor (MG132), a translation inhibitor (cycloheximide), or an mTOR inhibitor (Rapamycin). If growth rates and cell cycle progression were independent of cell size, both large and small cells would be equally affected by any treatment. Our results show that MG132 increased the variation in the size of cells at G1/S. (Fig. 4B). Cycloheximide had the opposite effect (Fig 4C). mTOR inhibition also decreased cell-to-cell size variability, but to a lesser extent than cycloheximide (Fig 4D). These results suggest that the decrease in cell size variance is at least partially driven by a cell-size discriminating proteasome activity. The possibility that size variation is further controlled by size dependent translation activity seems less likely in light of the decreased size variation following cycloheximide treatment.
Figure 4.
Cell size variability (full width/half maximum) as a function of cell cycle time for HeLa cells incubated for 1hr with (A) 0.001 v/v Dimethylsulfoxide; (B); 1uM cycloheximide; (C ); 10uM G132; M (D) 100nM rapamycin. Confidence intervals are shown in gray.
Proliferating cells in an unsynchronized population are distributed among different molecular states (i.e. cell cycle stages). In situations where this distribution does not change with time and where individual cells shift from state to state in a defined sequence, it is possible to calculate dynamical features from simple static single cell measurements9,10 which may be obtained from microscopy or flow cytometry., We have showed that both our primary measurements and the functions derived from them are time-invariant (see Supplementary material), thereby meeting these criteria. Others11 previously suggested that data from fixed cells could, in principle, be used to extract dynamic information; we have now provided an explicit mathematical framework to make this analysis possible. Using ERA we show that cell-to-cell size variation is regulated by a negative feedback at the G1/S transition. We can also use ERA to characterize other dynamic processes that cannot in general be measured in real time in living cells, such as the temporal changes in phosphoproteins during the cell cycle (Supplementary material)
Methods Summary
Reagents, cells and antibodies are described in the supplement. Cells were plated and fixed at 105 cells per ml in 15cm dishes. They were fixed in paraformaldehyde, permealized and stained with 0.04 ug/ml succinimidyl ester linked Alexa dyes diluted in DMSO (Alexa Fluor 647 carboxylic acid, succinimidyl ester, Invitrogen, A-20106). Slides were imaged on a with a Nikon Ti Inverted Fluorescence Microscope with Perfect Focus controlled by Nikon Elements software. We used the scan-slide function to image the full area of the slide at 20× magnification. Image analysis was performed with custom written software (EnsembleThresher). The details of the software and the calculation of the ERA parameters are discussed in detail in the supplement.
Supplementary Material
Supplemental data
Acknowledgements
We thank Allon Klein, Yifat Merbl, Shay Tal and Jared Toettcher for consistent and valuable insights at the beginning of and throughout this project. We thank Jennifer Waters and the staff of The Nikon Imaging Center at Harvard Medical School for help and support. We especially thank Rebecca Ward for her critique of the paper and the National Institute of General Medical Sciences (GM26875) for support of this work.
Footnotes
Author Contributions
R.K. and J.L. developed the method (ERA) for extracting dynamic information and calculating feedback spectra from fixed populations, designed algorithms, wrote all image-processing software and analyzed data. R.K. designed all experiments, and wrote the manuscript. J.L. contributed significantly to all conceptual challenges and to writing the manuscript. M.B.G. contributed conceptually, made important measurements and calculations and contributed to the writing of the manuscript. S.O. provided interferometry-derived cell mass measurements. G.L. and M.W.K. contributed to the formulation of the problem, development of the ideas and the writing of the manuscript.
References cited
- 1.Mitchison JM. Growth during the cell cycle. Int Rev Cytol. 2003;226:165–258. doi: 10.1016/s0074-7696(03)01004-0. [DOI] [PubMed] [Google Scholar]
- 2.Deen WM. Analysis of transport phenomena. 2nd edn Oxford University Press; 2012. [Google Scholar]
- 3.Sakaue-Sawano A, et al. Visualizing spatiotemporal dynamics of multicellular cell-cycle progression. Cell. 2008;132:487–498. doi: 10.1016/j.cell.2007.12.033. doi:10.1016/j.cell.2007.12.033. [DOI] [PubMed] [Google Scholar]
- 4.Mitchison JM. The biology of the cell cycle. University Press; 1971. p. 128. [Google Scholar]
- 5.Popescu G, et al. Optical imaging of cell mass and growth dynamics. Am J Physiol Cell Physiol. 2008;295:C538–544. doi: 10.1152/ajpcell.00121.2008. doi:10.1152/ajpcell.00121.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mir M, et al. Optical measurement of cycle-dependent cell growth. Proc Natl Acad Sci U S A. 2011;108:13124–13129. doi: 10.1073/pnas.1100506108. doi:10.1073/pnas.1100506108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Son S, et al. Direct observation of mammalian cell growth and size regulation. Nat Methods. 2012;9:910–912. doi: 10.1038/nmeth.2133. doi:10.1038/nmeth.2133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Killander D, Zetterberg A. A quantitative cytochemical investigation of the relationship between cell mass and initiation of DNA synthesis in mouse fibroblasts in vitro. Exp Cell Res. 1965;40:12–20. doi: 10.1016/0014-4827(65)90285-5. [DOI] [PubMed] [Google Scholar]
- 9.Hendrix RW, Zwaan J. Cell shape regulation and cell cycle in embryonic lens cells. Nature. 1974;247:145–147. doi: 10.1038/247145a0. [DOI] [PubMed] [Google Scholar]
- 10.Tzur A, Kafri R, LeBleu VS, Lahav G, Kirschner MW. Cell growth and size homeostasis in proliferating animal cells. Science. 2009;325:167–171. doi: 10.1126/science.1174294. doi:10.1126/science.1174294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jacobberger JW, Avva J, Sreenath SN, Weis MC, Stefan T. Dynamic epitope expression from static cytometry data: principles and reproducibility. PLoS One. 2012;7:e30870. doi: 10.1371/journal.pone.0030870. doi:10.1371/journal.pone.0030870. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental data