Size-dependent control of colloid transport via solute gradients in dead-end channels (original) (raw)

Significance

Dead-end geometries are commonly found in many porous systems. Particle transport into such dead-end pores is often important, but is difficult to achieve owing to the confinement. It is natural to expect that Brownian motion is the sole mechanism to deliver the particles into the pores, but that mechanism is, unfortunately, slow and inefficient. Here, we introduce solute gradient to control the transport of particles in dead-end channels. We demonstrate a size effect such that larger particles tend to focus more and reside deeper in the channels. Our findings suggest a potential pathway to many useful applications that are difficult to achieve in dead-end geometries such as particle sorting and sample preconcentration, which are important in pharmaceuticals and healthcare industries.

Keywords: colloid, diffusiophoresis, solute gradient, size effect, dead-end channel

Abstract

Transport of colloids in dead-end channels is involved in widespread applications including drug delivery and underground oil and gas recovery. In such geometries, Brownian motion may be considered as the sole mechanism that enables transport of colloidal particles into or out of the channels, but it is, unfortunately, an extremely inefficient transport mechanism for microscale particles. Here, we explore the possibility of diffusiophoresis as a means to control the colloid transport in dead-end channels by introducing a solute gradient. We demonstrate that the transport of colloidal particles into the dead-end channels can be either enhanced or completely prevented via diffusiophoresis. In addition, we show that size-dependent diffusiophoretic transport of particles can be achieved by considering a finite Debye layer thickness effect, which is commonly ignored. A combination of diffusiophoresis and Brownian motion leads to a strong size-dependent focusing effect such that the larger particles tend to concentrate more and reside deeper in the channel. Our findings have implications for all manners of controlled release processes, especially for site-specific delivery systems where localized targeting of particles with minimal dispersion to the nontarget area is essential.

The ability of a particle to migrate along a local solute concentration gradient, which is referred to as diffusiophoresis, has been exploited to direct transport in a variety of systems, e.g., artificial swimmers (1, 2) and collective behaviors of active colloids (3, 4). One physical mechanism for diffusiophoresis originates from surface–solute interactions, where the solute gradient sets up an osmotic pressure gradient within a narrow interaction region. This gradient leads to fluid flow along the surface of a particle, in which case propulsion occurs in the opposite direction and is referred to as chemiphoresis (5, 6). In addition, differences in diffusivities between anions and cations lead to spontaneous electrophoresis of a particle, giving an additional propulsion mechanism. A particular feature of diffusiophoresis is that the diffusiophoretic mobility, or the phoretic velocity, of a particle is independent of its size, as long as the thickness of the interaction region, e.g., the Debye screening layer when the interaction is electrostatic, is much thinner than the size of the particle (6). This feature allows the utilization of diffusiophoresis for enhancing transport of microscale particles, leading to orders of magnitude higher transport rates compared with pure diffusion (7). However, this size independence could also be a source of frustration because it precludes useful effects such as sorting or controlling transport by particle size.

We anticipate that size-independent particle mobility breaks down when the thickness of the surface–solute interaction region becomes comparable to the size of the particle. Already more than a century ago this feature has been well appreciated in the field of electrokinetics as the Hückel limit (8) where the electrophoretic mobility of a particle is 2/3 of the Smoluchowski mobility if the thickness of Debye screening layer κ−1 is larger than the particle radius a, i.e., κa<1. Likewise, there are a number of investigations, mostly theoretical, on the effect of finite Debye layer thickness on the diffusiophoretic mobility, which have shown that the influence of finite κa is much stronger than for electrophoresis due to the presence of chemiphoresis (9–11). Because a finite Debye layer effect can lead to size-dependent particle mobility, we revisit the influence of finiteness of κa on the diffusiophoretic mobility, and exploit it in a useful way.

One application of size-dependent diffusiophoresis is particle transport into dead-end geometries, which is important to many industrial applications including drug delivery and disinfection. When characterizing transport processes, transferring fluid and/or particles into dead-end geometries or pores is a significant challenge as such geometries do not allow any net fluid flow within the system. Recently, it has been shown that diffusiophoresis can be used to pump colloidal particles and oil emulsions in and out of dead-end capillaries, which have significant implications for oil recovery systems (12).

Here, we use size-dependent diffusiophoresis to control colloid transport in a dead-end channel. The observed size dependence is attributed to the abovementioned finite Debye layer effect. This key insight can be exploited pragmatically, to achieve useful end points such as size-dependent particle sorting and separation. We show that theory accounting for finite κa is in a good agreement with the experimental observations.

Further, we demonstrate that a judicious choice of ions for multicomponent solutes can also be used to gain exquisite control of the phenomenon, importantly at constant osmolarity, which is critical for in vivo applications, either preventing colloid particles from entering a dead-end channel, or promoting entry as for a single binary ionic solute such as NaCl. These observations suggest future applications in drug delivery (13, 14).

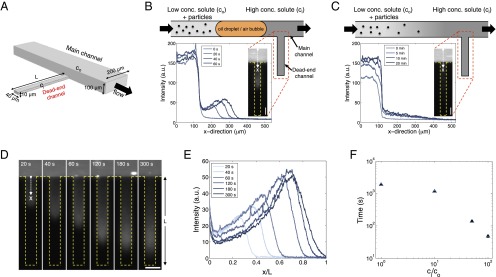
To impose a solute gradient along a dead-end channel, we have used a microfluidic approach (Fig. 1_A_), where the entrance of the dead-end channel is connected to the main flow channel so that the solute concentration (co) can be regulated at the entrance. Additionally, the height of the dead-end channel is much thinner (≈10 μm) than the main channel (≈100 μm), such that the disturbance from the main channel can be minimized (15).

Fig. 1.

Fig. 1.

Colloid transport in a dead-end channel induced by a solute gradient. (A) Setup for enabling transport experiments in a dead-end channel with minimum disturbance from a continuous flow. (B) Steplike initial solute and colloid concentrations were realized by inserting an oil droplet or an air bubble in between two liquids with different solute concentrations. (C) Otherwise, a gradual concentration was observed due to mixing. Insets are the fluorescent intensity distributions of colloidal particles (polystyrene latex beads, diameter 0.19 μm) along the dead-end channel. (D) Sequential images and (E) intensity distributions of colloids (particle diameter 0.19 μm) migrating along a dead-end channel in the presence of a solute gradient (NaCl: ci = 2 mM, co = 0.02 mM). Channelwise direction, x, is normalized by the length of the dead-end channel, L (=400 μm). (F) Time taken for the colloidal particles to reach the middle of the dead-end channel with 50% of the inlet fluorescent intensity (0.5Ii) under different solute gradients. (Scale bars: 50 μm.)

Moreover, unlike electrophoresis or thermophoresis, where the field gradient is generally constant, diffusion in a dead-end channel is time dependent. Therefore, to observe the transient dynamics, especially at the early stages of the solute and colloid transport, a steplike initial concentration profile is desired. To achieve this condition, we inserted in the main channel an immiscible fluid such as an oil droplet or an air bubble to separate the leading solution, which fills in the dead-end channel first, with the trailing solution that has different solute conditions and contains the colloidal particles (Fig. 1_B_). This sequential approach works as an effective gate leading to a repeatable constant inlet concentration at the start of the experiment. In the absence of this flow design, the trailing fluid that contains the colloidal particles will be mixed with the leading fluid during the delivery to the inlet of the dead-end channel. This results in >10 min of dead time before the steady-state inlet condition is reached (Fig. 1_C_); such a delay would obscure and compromise the results we report here.

Using this setup, we study the colloid transport in a dead-end channel induced by a solute gradient. Because the colloidal particles migrate toward higher solute concentrations with our current choice of solutes, we keep the initial inner solute concentration (ci) high and the outer solute concentration (co) low, unless otherwise noted. Typical transport dynamics of colloids in the presence of a solute gradient are shown in Fig. 1 D and E and Movie S1. Owing to the solute (NaCl) gradient, the colloid transport into the dead-end channel is accelerated by nearly two orders of magnitude compared with the pure diffusion case (i.e., no solute gradient) as shown in Fig. 1_F_.

The enhanced colloid transport is not surprising as it has already been reported in a number of studies (7, 16, 17). However, we have also observed that the density profile of the leading colloids is nonuniform in the lateral direction, and the colloidal particles tend to concentrate as they transport along the channel (Fig. 1 D and E). These features stem from the intrinsic geometrical confinement of the dead-end channel. In the presence of a solute gradient along a channel, a diffusioosmotic flow is induced, which has a pluglike flow profile. Because a dead-end geometry does not allow any net flux, a pressure gradient is established that opposes the osmotic flow. In consequence, as the pressure-driven flow has an essentially parabolic profile, summing up these two components results in a circulating flow where the velocity at the center of the channel is opposite to the wall slip velocity. This flow is analogous to an electrokinetic pump where an electroosmotic flow that is induced by an external electric field is balanced by a Poiseuille flow in a dead-end channel and leads to a circulating flow developed nearly instantaneously within the entire channel (18).

In our system, because the solute concentration is diffusing out over time (ci>co), the circulating flow slowly propagates toward the closed end of the channel (Supporting Information, Movie S2). Along with this flow, particles experience phoretic motion, and thus the net motion of the particles is the sum of the fluid flow and the phoretic movement, which leads to the lateral curvature of the density profile, as also observed in a recent study by Kar et al. (12).

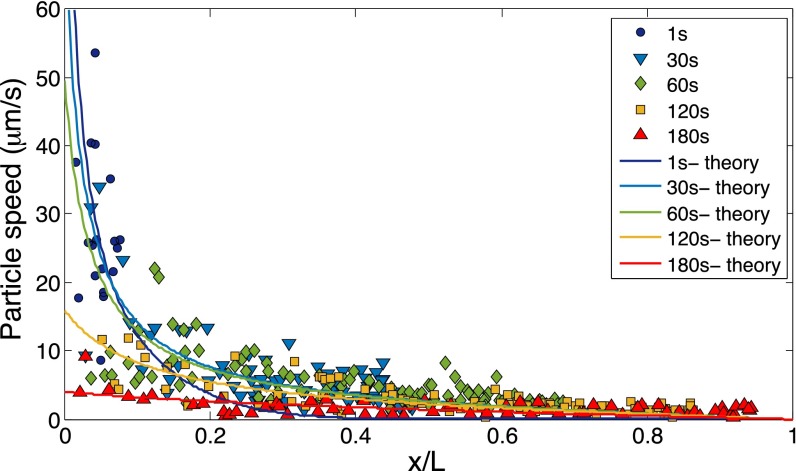
The transient nature of solute diffusion in a dead-end channel also leads to another significant effect: particle focusing. Because the gradient of the solute concentration is always decreasing along the channel due to diffusion, the particle phoretic velocity, which is proportional to ∇lnc, decreases as the particles move deeper into the channel (Fig. S1). Thus, particles tend to accumulate near the leading edge of the migrating colloidal front (17, 19), which creates a pluglike colloidal “wave” that can be quantitatively identified from the time-dependent fluorescence intensity distribution along the channel (Fig. 1 D and E).

Fig. S1.

Fig. S1.

Measurement of the particle (diameter 1.01 μm) speed along the dead-end channel driven by a solute gradient (NaCl: ci=2 mM, co=0.02 mM). Solid curves represent theoretical results.

This colloidal wave leads to preconcentration, separation, and sorting of particles, which could be useful to many applications. The quantitative factors that define the colloidal wave are the location of the peak, the amplitude, and the width of the wave. In theory, these factors are set by the transport properties of the particle and the solute, namely the diffusiophoretic mobility of the particle (Γp) and diffusivity of the particle (Dp) and the solute (Ds). In detail, the transient distribution of colloids (concentration n) in the presence of a solute gradient can be described by an advection–diffusion equation that is coupled to the solute diffusion, which drives the advection of colloids. The velocity of the particles is defined as v=vp+vf where vp=Γp∇lnc is the particle velocity driven by diffusiophoresis and vf is the flow velocity driven by solute gradient (see Supporting Information for full derivation of vf). Using the conservation law ∂n/∂t + ∇ ⋅ j = 0, where j = −Dp∇n + vn is the particle flux, the dimensionless equation for the colloid density N can be expressed as

∂N∂τ=DpDs∇2N−ΓpDs∇(N∇lnC)−∇⋅(VN), [1]

where C is the dimensionless solute concentration, τ is the dimensionless time (tDs/L2, where L is a characteristic length scale), and V is the dimensionless fluid velocity, which is defined as V=vfL/Ds. The first term on the right-hand side of Eq. 1 represents the diffusion of colloids, whereas the latter terms represent the colloid advection driven by a solute gradient.

In general, Γp is commonly regarded as a size-independent value in the thin Debye layer approximation (κa→∞). When the thickness of the Debye layer becomes comparable to the size of the particle, the diffusiophoretic mobility becomes size dependent, Γp(κa). Following the pioneering work of Prieve and coworkers (9, 10), the size-dependent diffusiophoretic mobility of the particles is expressed as

Γp=ϵ2η(kBTZe)2u01−u1/(u0 κa), [2]

where ϵ is the permittivity of the medium, η is the viscosity of the medium, kB is the Boltzmann constant, T is the temperature, Z is the valence of the solute, and e is the elementary charge. Also, u0 and u1 are functions of the zeta potential. The lowest order contribution for very large particles or vanishing thickness of the Debye layer (κa→∞) is

u0=2βZeζpkBT+8 ln cosh(Zeζp4kBT). [3]

Here, ζp is the zeta potential of the particles and β=(D+−D−)/(D++D−), where D+ and D− are the diffusivities of cations and anions, respectively. The first and second terms on the right-hand side of Eq. 3 represent electrophoresis and chemiphoresis, respectively. For u1, lengthy expressions can be found in (9) (see Supporting Information for further discussion).

A remarkable fact is that even when κa≈100, unlike electrophoretic mobility (20), the predicted diffusiophoretic mobility deviates noticeably from Γp(κa→∞) (10). When κa≈10, which is a general condition for common diffusiophoresis experiments (7, 12, 16, 17), the diffusiophoretic mobility is predicted to be almost an order of magnitude lower, depending on ζp (10). Our experimental conditions are in a similar range, κa≈2−40 [κ−1=13.6 nm when c=(ci+co)/2≈1 mM], indicating that size effects can be significant.

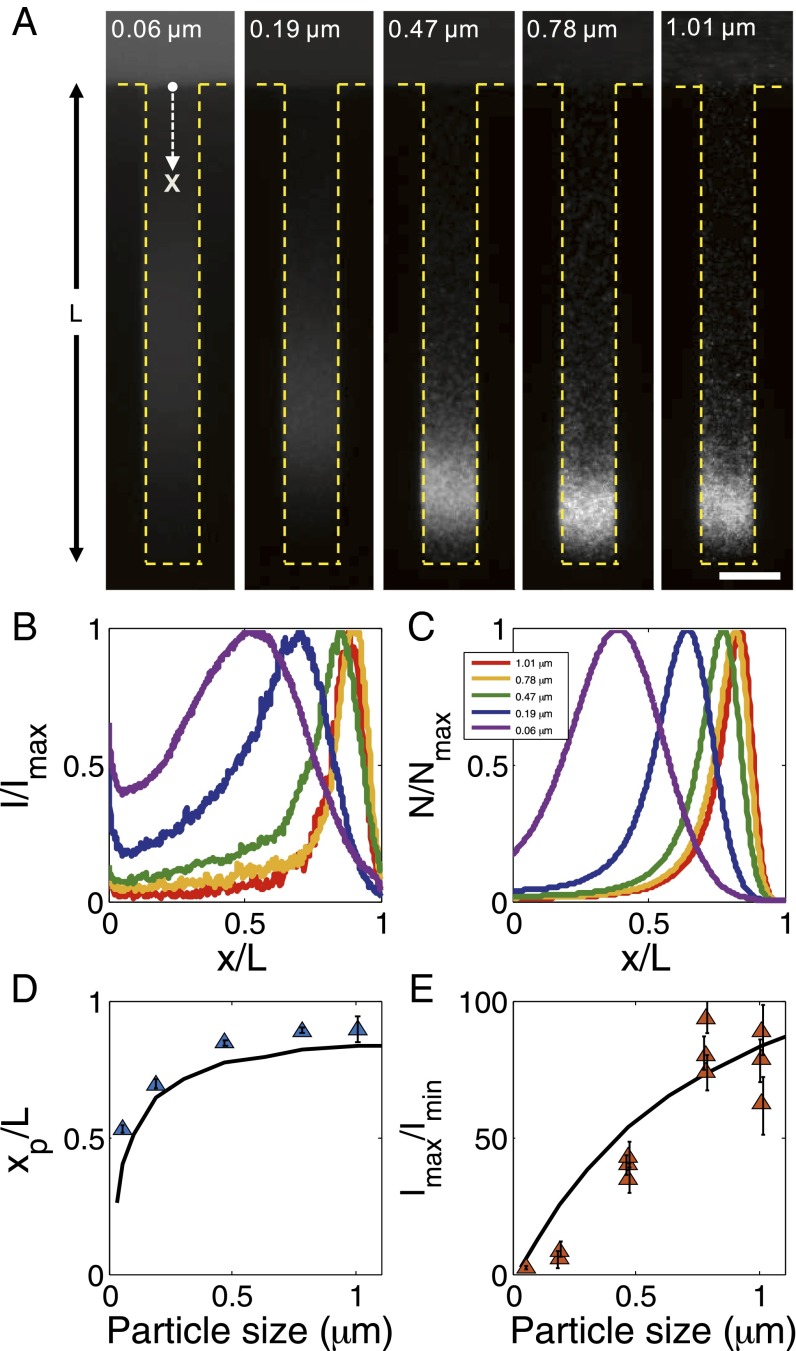
The diffusiophoresis of particles with different sizes in a dead-end channel is shown in Fig. 2. Owing to the broad range of κa, we observe strong size-dependent particle focusing, where the larger particles tend to reside deeper in the channel, and they generally tend to concentrate more (Fig. 2_A_ and Movie S3). For instance, the smallest particles (2a=0.057 μm) show a focusing ratio of about 2, and the terminal peak position xp is about 50% of the channel length L at t=300 s, whereas, the largest particles (2a=1.01 μm) show a focusing ratio as large as 100, and the particles travel nearly to the end of the channel without noticeable dispersion (Fig. 2 D and E).

Fig. 2.

Fig. 2.

Size-dependent particle focusing driven by a solute gradient (NaCl: ci = 2 mM, co = 0.02 mM). (A) Fluorescent images and (B) intensity distributions of colloids with different diameters ranging from 0.06 to 1.01 μm at t = 300 s. The intensity I is normalized by the maximum intensity Imax. (C) Theoretical prediction for colloid density profiles with different diameters at t = 300 s. Plot of (D) peak position (xp) and (E) focus magnitude (Imax/Imin, Imin is the minimum intensity near the inlet) for various particles at t = 300 s obtained from B. Black curves represent theoretical predictions. (Scale bar: A, 50 μm.)

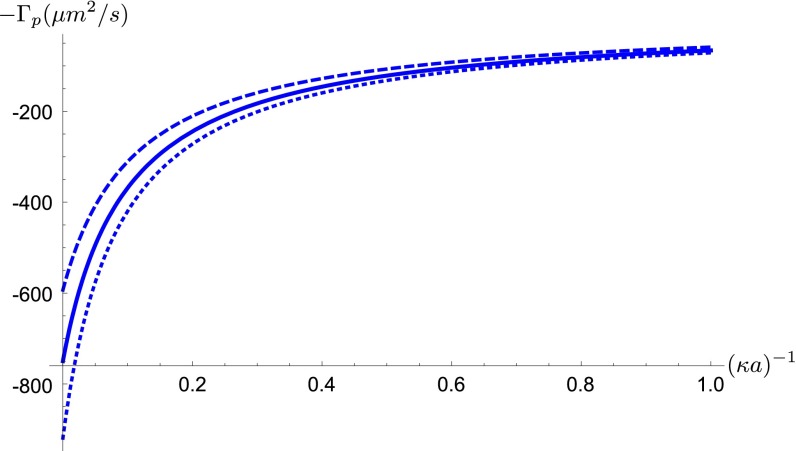
For a given zeta potential (−70 mV), Γp is estimated to vary by almost a factor of 5 based on Eq. 2 for our range of particle sizes (Fig. S3). Considering that Dp also changes significantly with size based on the Stokes–Einstein relation, a combination of diffusiophoresis and Brownian diffusion leads to a strong size effect, which is confirmed from a good agreement between the experiment and the theory based on Eqs. 1 and 2 (Fig. 2 B and C). The discrepancy near the entrance of the channel for small particles shown in Fig. 2_C_ mainly comes from the penetration of the fluorescent signal coming from the main channel because of the strong optical density required for small particles.

Fig. S3.

Fig. S3.

Dependence of particle diffusiophoretic mobility Γp on the particle radius a and the Debye layer thickness κ−1. Solid line: ζp=−70 mV, Dotted line: ζp=−80 mV, Dashed line: ζp=−60 mV.

Other possible size-dependent phenomena include particle–particle interactions (5), wall interactions (21), hydrodynamic dispersion (22), gravimetric effects (21), electrokinetic lift (23), etc., but we argue that these effects are negligible compared with the finite κa effect (detailed discussion in Supporting Information). Note that the presence of the fluid advection does not significantly influence the particle transport, but only contributes to the lateral inhomogeneity in the early stage, which is confirmed by comparing the theoretical results with and without the solute gradient-induced fluid advection (Figs. S4 and S7; Supporting Information).

Fig. S4.

Fig. S4.

Calculated colloid transport in the presence of a solute gradient. (A) Solute distribution versus time. Particle distribution versus time for (B) small particles (diameter 0.06 μm) and (C) large particles (diameter 1.01 μm). Solid lines indicate calculations with fluid advection induced by solute gradient, whereas dashed lines indicate calculations without fluid advection.

Fig. S7.

Fig. S7.

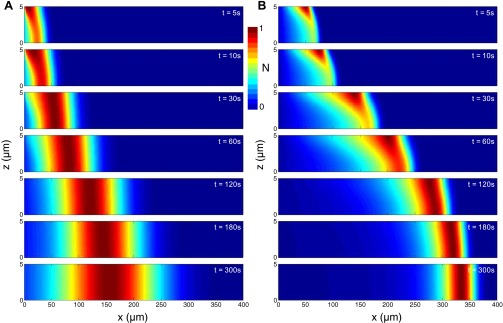
Numerical simulation results of the side view (x_–_z plane) of the particle migration along a dead-end channel driven by a solute gradient in the presence of flow advection; z=0 refers to the centerline of the channel, such that the images represent upper half of the channel. Particle size: (A) 0.06 and (B) 1.01 μm.

All of the demonstrated results so far were driven by a single solute gradient with a contrast of 100 (NaCl: ci = 2 mM, co = 0.02 mM), which may be limited for practical applications, especially with in vivo drug delivery where a strong solute gradient may lead to an osmotic shock. Thus, to seek broader insights of diffusiophoresis so as to gain further control over the movement of colloidal particles, we focus on the role of individual mechanisms that contribute to the overall transport. Recall that diffusiophoresis has two contributions, one from chemical potential differences (chemiphoresis), and the other from differences between the diffusivities of anions and cations, which creates a local electric field (electrophoresis). Considering that the diffusivity of K+ is nearly identical to that of Cl− (DK+/DCl− = 0.97, cf. DNa+/DCl− = 0.66; ref. 24), we suggest that there can be an alternative strategy to control colloid transport besides a single solute gradient: by displacing a solute with another solution containing different species. Analogous to a liquid junction potential (25, 26), the interdiffusion of multicomponent solutes having equimolar concentration also generates a spontaneous electric field that can allow electrophoresis. For instance, the interdiffusion of NaCl and KCl solutions can generate an electric field of ∼40 V/m, which is comparable to the single solute (NaCl) gradient case (Supporting Information).

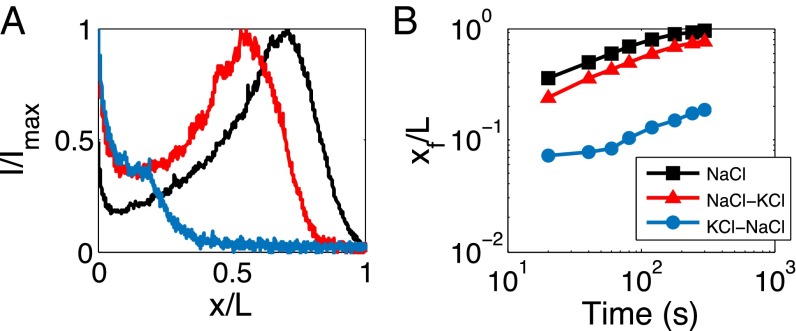
Using this strategy, we can create a local electric field that gives rise to the electrophoresis of the particles in the channelwise direction so that the colloid transport into the channel is enhanced by locating NaCl inside the dead-end channel and displacing it with KCl, which flows through the main channel. As illustrated in Fig. 3 A and B (Movie S4), we show that this strategy allows particle focusing and fast colloidal transport that is comparable to the single solute gradient case (black curves). This “displacement” strategy is desired when a constant osmolarity of the solution is required, such as with in vivo transport systems.

Fig. 3.

Fig. 3.

Interdiffusion of equimolar multicomponent solutes (ci = co = 2 mM) for inducing diffusiophoresis in a dead-end channel under constant osmolarity. (A) Fluorescent intensity distribution at 300 s and (B) trace of front position, xf=x(i=0.2Ii), for different solute configurations (blue: inner = KCl, outer = NaCl; red: inner = NaCl, outer = KCl). Results of a single solute with a gradient (NaCl: ci = 2 mM, co = 0.02 mM) are presented in black for comparison.

Likewise, if we place NaCl and KCl in the opposite configuration, the electric field is now generated in a reverse direction, which is expected to slow down the colloid transport. Indeed, such an initial distribution of electrolyte completely prevents the colloidal particles from going into the channel until the electric field has vanished (blue curve in Fig. 3_B_; Movie S4). This effect lasts for over a minute, which is the same order of magnitude as the solute diffusion time, L2/Ds∼100 s. This approach may have a significant implication in programmable drug delivery applications where such an electric field can serve as a trigger for drug release (27).

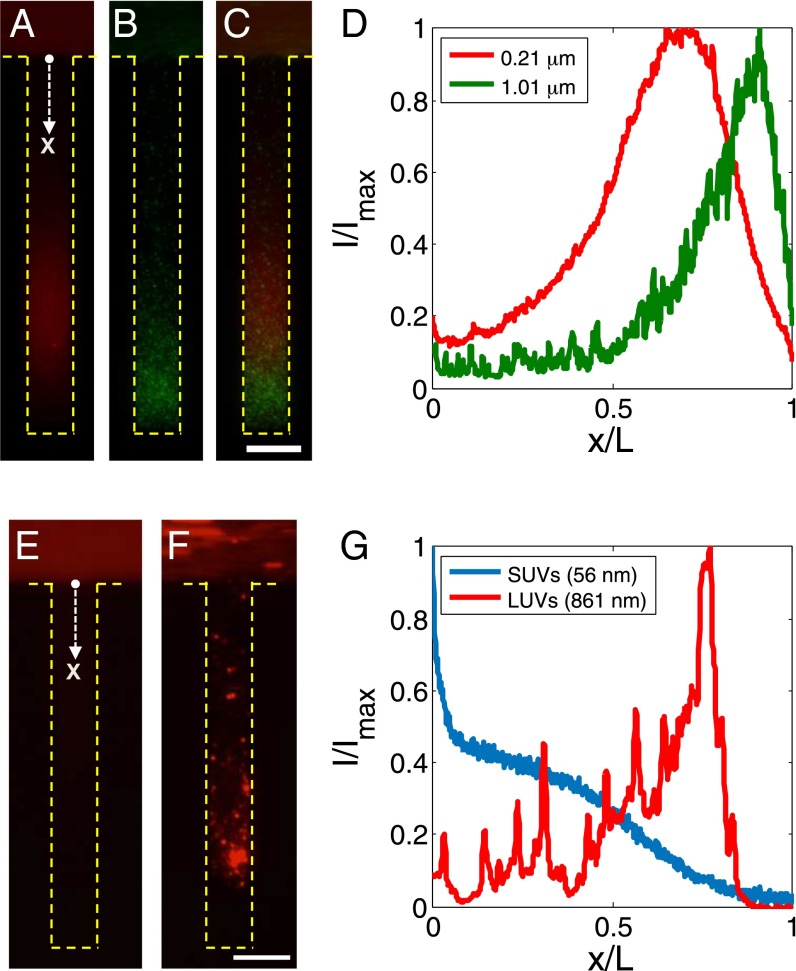
We have demonstrated an effective way of delivering colloidal particles into dead-end channels by imposing solute gradients, either by a single solute gradient, or by multispecies interdiffusion. We further demonstrated that size-dependent diffusiophoresis can be obtained by controlling κa, a fact that is commonly ignored. A key observation regarding the size-dependent diffusiophoresis is that there is a tendency for the larger particles to focus more and transport farther into the channel, which suggests many technological implications such as particle sorting that are otherwise difficult to achieve in dead-end geometries. As demonstrated in Fig. 4 A–D (Movie S5), particle sorting from a mixture of two (or more) particles having different sizes can be simply achieved. This feature is enabled by the fact that particle–particle interactions are very weak for phoretically driven particles such that the particles are easily separated without interfering with neighboring particles (5).

Fig. 4.

Fig. 4.

Control of colloidal particles in dead-end channels via a solute gradient for various applications. (A–D) Size-dependent particle sorting from mixture of particles in a dead-end channel driven by a solute gradient (NaCl: ci = 2 mM, co = 0.02 mM). The mixture consists of polystyrene particles having diameters of 0.21 and 1.01 μm dyed with different fluorophores. (A–C) Fluorescent images of (A) diameter = 0.21 μm particles and (B) 1.01 μm particles at t = 300 s, and (C) intensity distributions of A and B along the channel. D is an overlaid image of A and B. (E–G) Control of lipid vesicles for drug delivery applications. Fluorescent images of (E) SUVs (mean diameter ≈ 56 nm) and (F) LUVs (mean diameter ≈ 861 nm), and (G) intensity distributions of the vesicles along the channel at t = 300 s. (Scale bars: 50 μm.)

In addition to particle sorting, size-dependent diffusiophoresis can be important especially in pharmaceuticals because it makes it possible to manipulate the final concentration and location of particles within deep pores with controlled dispersion based on their sizes. As an example, delivery of lipid vesicles (lipid composition is provided in Materials and Methods) in deep pores can be manipulated via imposing a solute gradient across the pore, where the peak penetration depth and the concentration ratio of the vesicles are controllable based on the size of the vesicles (Fig. 4 E–G and Movie S6). This demonstration implies the possible application of size-dependent diffusiophoresis in site-specific delivery systems where localized targeting of particles with minimal dispersion to the periphery is desired (14).

Materials and Methods

Materials.

Fluorescent polystyrene latex particles were purchased from Bangslab. NaCl, KCl, EDTA, Hepes, NaOH, and chloroform were purchased from Sigma Aldrich. 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dioleoyl-sn-glycero-3-phospho-l-serine (sodium salt) (DOPS), and 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-_N_-(lissamine rhodamine B sulfonyl) (ammonium salt) (Rh-DPPE) were purchased from Avanti Polar Lipids. Polydimethylsiloxane (PDMS) was purchased from Dow Corning (Sylgard 184).

Sample Preparations.

The polystyrene latex particles were dispersed in either NaCl or KCl solutions prepared from deionized water with concentration of 0.05 wt%. Lipid vesicles were prepared from a lipid mixture of DOPC/DOPS/Rh-DPPE in a 89.5/9.5/1 mol% ratio dissolved in chloroform. Small unilamellar vesicles (SUVs) were prepared via the standard sonication method (28); 1 mg of lipid mixture was dried overnight under vacuum. Then, the dried lipids were rehydrated with a buffer solution (0.5 mM Hepes, 0.5 mM EDTA, adjusted with 1 M NaOH to pH≈ 8) followed by sonication using a tip sonicator for 10 min. Large unilamellar vesicles (LUVs) were prepared via the electroformation method (29). Fifty μg of lipid mixture was spread on the surfaces of indium tin oxide (ITO) glass slides, then dried overnight under vacuum. The ITO glass slides were separated by a PDMS gasket, which was filled with Hepes buffer solution. An AC electrical field (1.7 Vpp, 10 Hz) was applied to the ITO glass slides for 30 min to form LUVs. The diameter and the zeta potential of the polystyrene particles and lipid vesicles were measured using Zetasizer Nano-ZS (Malvern Instruments).

Experimental Setup.

All channels were made from PDMS with a two-step lithography process for making a thin dead-end channel (∼10 μm) that is connected to the thick main channel (∼100 μm). The ratio between the elastomer base and the cross-linker was 10:1.5 to enhance the stiffness of the channels. The channels were sealed with the same PDMS slab to ensure that all of the surfaces are the same. The fabricated PDMS channels were immersed in aqueous solution overnight before the experiments to prevent water permeation. The flow rate was controlled using a feedback-controlled pump (MFCS-EZ; Fluigent) that is equipped with a precise flow meter (Flowunit; Fluigent). Under the low Reynolds number flow conditions that apply here, the main channel flow penetrates a distance of order ∼10 μm into the side channel. The Péclet number at the entrance, Uw/Ds, where U is flow velocity near the entrance of the dead-end channel (≈10 μm/s), w is the width of the channel (40 μm), and Ds is the solute diffusivity (≈1.5×10−9 m2/s), can be reduced below 1, so the advection from the main flow can be neglected.

Particle Speed Measurements

The speed of the particles was obtained by correlating two consecutive image frames (time interval 0.2 s). Only particles near the centerline of the channel were measured (Fig. S1).

Modeling of the Particle Dynamics

Governing Equations.

The time-dependent migration of particles induced by a solute gradient can be described by an advection–diffusion equation that is coupled to the diffusion equation for solutes. The model domain is illustrated in Fig. S2, where the length of the dead-end channel is L, the colloidal particles are in a well-mixed reservoir at the left end, and the colloidal particles are migrating toward the dead end of the channel.

Fig. S2.

Fig. S2.

Schematic illustration of a dead-end channel with length L and height 2h.

The diffusion equation for determining the solute concentration distribution within this domain is expressed as

where c is the solute concentration and Ds is the ambipolar diffusion coefficient for the solute. Ds is defined as Ds≡2D+D−/(D++D−), where D+ and D− are the diffusivities of cations and anions, respectively. The boundary condition is given by c=co at x=0, and the initial condition is given by c=ci at t=0. Owing to the boundary condition, c is independent of y and z, i.e., c(x,y,z,t)=c(x,t). The solution to Eq. S1 under given conditions is

c(x,t)=co+(ci−co)∑n=0∞bn⁡sin(λnx/L)e−λn2Dst/L2, [S2]

where bn=2(1−⁡cos⁡λn)/λn and λn=(2n+1)π/2.

The solute concentration gradient drives the colloid migration. Assuming that the concentration gradient can be linearized on the scale of the particles, the diffusiophoretic velocity is given by (6)

where vp is the particle velocity and Γp is the diffusiophoretic mobility of a particle. On top of particle diffusiophoresis, the solute gradient induces flow advection vf, which is a consequence of balance between diffusioosmosis and Poiseuille flow. The diffusioosmotic flow is driven by a wall slip velocity of vf,wall=−Γw∇ln⁡c, where Γw is the diffusiophoretic mobility of the wall. This flow is further derived in the following section.

Denoting v = vp + vf, we can obtain the time-dependent particle dynamics using the advection–diffusion equation

where n is the colloid density and Dp is the particle diffusivity. The boundary condition is given by n=ni at x=0, and the initial condition is given by n=0 at t=0, because the channel initially contains no particles.

Following the work of Prieve (9, 10), the diffusiophoretic mobility of the particles is estimated using the fact that the Debye layer thickness κ−1 is smaller than the particle radius a. We have

Γp=ϵ2η(kBTZe)2u01−u1/(u0 κa), [S5]

where ϵ is the permittivity of the medium, η is the viscosity of the medium, kB is the Boltzmann constant, T is the temperature, Z is the valence of the solute, and e is the elementary charge; u0 and u1 are functions of the zeta potential. The lowest order contribution for very large particles or vanishing thickness of the Debye layer (κa→∞) is

u0=2βZeζpkBT + 8 ln cosh(Zeζp4kBT). [S6]

Here, ζp is the zeta potential of the particles and β=(D+−D−)/(D++D−). The first and second terms on the right-hand side of Eq. S6 represent electrophoresis and chemiphoresis, respectively. For u1, lengthy expressions can be found in ref. 9. In principle, this correction for finite Debye layer thickness depends on the details of the flow field around the colloid, which is affected in our case by the Poiseuille-like channel flow. With the channel height 2_h_, the corrections due to channel flow are of order (a/(2h))2≃10−2 and have thus been neglected. Solute convection outside the diffuse layer could also affect the diffusiophoretic speed (30). However, the Péclet number of the solute is estimated as vpa/Ds≈10−2, which allows to neglect convection in our case. Fig. S3 shows the mobility estimates for particles with ζp=−70 mV in a NaCl solution as used in this work.

For estimating the wall slip velocity vf,wall we assume that corrections ∼(κL)−1 due to the finite thickness of the Debye layer are negligible. Thus, we have

Γw=ϵη(kBTZe)2(βZeζwkBT+4ln cosh(Zeζw4kBT)), [S7]

where ζw is the zeta potential of the wall.

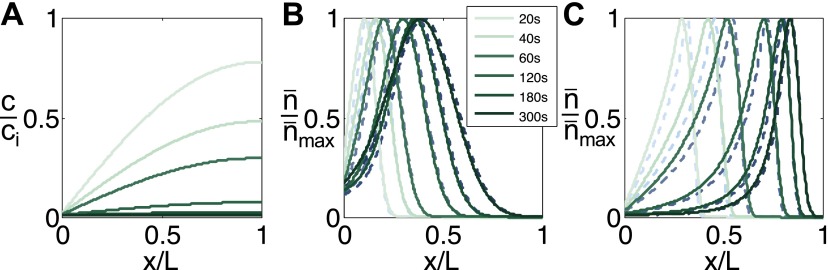
Taking ζp=−70 mV and ζw=−30 mV (31), we obtain Γp≈270 and 610 μm2 s−1 for the particles with diameter of 0.06 and 1.01 μm, respectively, and Γw≈210 μm2 s−1. The results obtained by solving Eq. S4 with these values are presented in Fig. S4; n¯ in Fig. S4 B and C is the particle concentration averaged along the depth direction, i.e., n¯=(2h)−1∫−hhn dz, where 2h is the height of the channel (10 μm). As presented, the size-dependent particle focusing behavior is clearly observed where the larger particles (Fig. S4_C_) tend to focus more and migrate deeper into the channel compared with the smaller particles (Fig. S4_B_). The solid lines indicate results obtained by neglecting the fluid advection, i.e., v=vp, whereas the dashed lines represent full consideration of the circulating flow, i.e., v=vp+vf. As shown, the presence of the fluid advection does not significantly influence the particle distribution. Only a slight deviation is observed at the early stage of the large particles due to the slow particle dispersion along the depth direction (z). This hydrodynamic dispersion is further dealt with below.

Fluid Advection Induced by Solute Gradient: Lubrication Approximation.

Consider diffusiophoretic flow in a dead-end channel. Here we treat a 2D problem, where the velocity field v(x,z)=(vx(x,z),vz(x,z)), with x the axial direction into the channel and z the depth direction, where the origin is the center of the channel. As a first step we assume that along the channel boundaries, there is a specified slip velocity vf,wall(x)=−Γw∇ln c, which is tied to gradient in the (logarithm of the) local concentration field. In the experiments the channel height 2h=10 μm and the transport occurs along a pore with length L≫h. Thus, as the local Reynolds numbers are small, and the thickness of the electrical double layer is assumed small compared with h, we solve Stokes equations, η∇2vf=∇p in the channel. The velocity profile is assumed to be symmetric about z=0, with vf=exvf,wall(x) along z=h. Because h≪L we use the lubrication approximation,

η∂2vx∂z2=∂p∂x and ∂p∂z=0, [S8]

and where vz is determined using the continuity equation, ∂vx/∂x + ∂vz/∂z = 0. The pressure gradient is established by enforcing that there is zero net volume flux across a cross-section of the channel. These steps lead to the axial velocity distribution

vx(x,z)=−Γw2d lncdx[3(zh)2−1]. [S9]

From continuity, and enforcing zero normal velocity at z=0 (the solution automatically satisfies zero normal velocity at z=h), we find

vz(x,z)=Γw2d2lncdx2[z((zh)2−1)]. [S10]

It should be noted that this lubrication flow is invalid at the far end (x=L) because it does not satisfy the no-slip boundary condition at the wall at the end of the channel. This effect should be order h, and is also small correction because the solute concentration gradient is always very weak at the far end.

Fluid Advection Induced by Solute Gradient: Lattice Boltzmann Simulation.

The lattice Boltzmann (LB) method is well suited to exploring the flow fields that are generated in dead-end channels by electroosmotic and diffusioosmotic wall slip boundary conditions. Here, LB is used to calculate the time-dependent 3D flow in a 200 × 40 × 10 μm dead-end channel, similar to the experimental situation. The results complement the lubrication solution in Eqs. S9 and S10 above. A shorter capillary than generally used in the experiments is chosen for numerical convenience, without losing any of the phenomenology. An animation of the flow field in the z midplane is shown in Movie S2.

For the calculation, we use an LB lattice with a grid spacing of 1 μm. Walls are added in the y and z planes and at one end of the channel in the x direction. The other end is open and a 40-μm gap is incorporated in the x direction beyond this point to represent the main channel. The walls are one LB-lattice-spacing thick. Thus, the LB calculation is run on a 240 × 42 × 12 lattice, with walls as just described, and periodic boundary conditions in the y and z directions in the gap region.

The y and z plane walls have assigned an _x_-dependent wall slip velocity in the x direction, derived from the salt concentration gradient via (as above)

vf,wall=−Γwd lncdx, [S11]

where Γw is the wall slip coefficient (which is related to the wall ζ potential). For the solute concentration we use c=co+(ci−co)erf(x/4Dst) which is the solution of Eq. S1 appropriate to the relatively short times considered here (Dst/L2≤0.043).

We use a double-relaxation-time D3Q15 LB scheme, with a rest state of weight 16, as described in refs. 32–34, to simulate Stokes flow (i.e., strict zero Reynolds number). For the stress relaxation parameter we use τ=0.8, which is known to have a good range of wave-vector-independent viscosity in terms of generalized hydrodynamics (33). The viscosity in the scheme is ν=(2τ−1)/6=0.1 in LB units. This sets the time scale over which the flow field reaches steady state: because the longest length is the capillary length, Lx=200 LB units, this time is of the order Lx2/ν=4×105 LB time steps.

Walls are implemented using the link-bounce-back method described by Ladd (35, 36); this ensures a stick boundary condition. To implement the wall slip velocity we apply a local, _x_-dependent body force in the fluid nodes immediately adjacent to the wall nodes. The overall scale of the local body force (and likewise the actual value of Γw) is immaterial in Stokes flow because it only serves to set the overall magnitude. Here the scale factor is chosen so that the maximum wall slip velocity at the starting time (where the velocity field is highest) is of order 0.1 in LB units; this limits compressibility artifacts. We initially tried to use Ladd’s link-bounce-back method for moving boundaries to represent the wall slip velocity field, but we found that this is marred by subtle numerical instabilities.

To make the individual movie frames, we impose the wall slip velocity according to Eq. S11 above, and run for 105 LB time steps to reach close to steady state according to the above estimate. This is done for 140 values of Dst (one for each frame of the movie) starting from Dst=50 and incrementing in steps of Dst=50. At the end point 4Dst=4×7,000≈170 so the salt concentration gradient has penetrated significantly more than half way into the capillary. For each value of Dst we sample the midheight velocity field, which has no z component by reflection symmetry. This (vx,vy) field is then used to generate an image frame containing representative streamlines, plus the vorticity (circulation) in the z direction represented as a color field. The stack of 140 image frames is assembled into Movie S2.

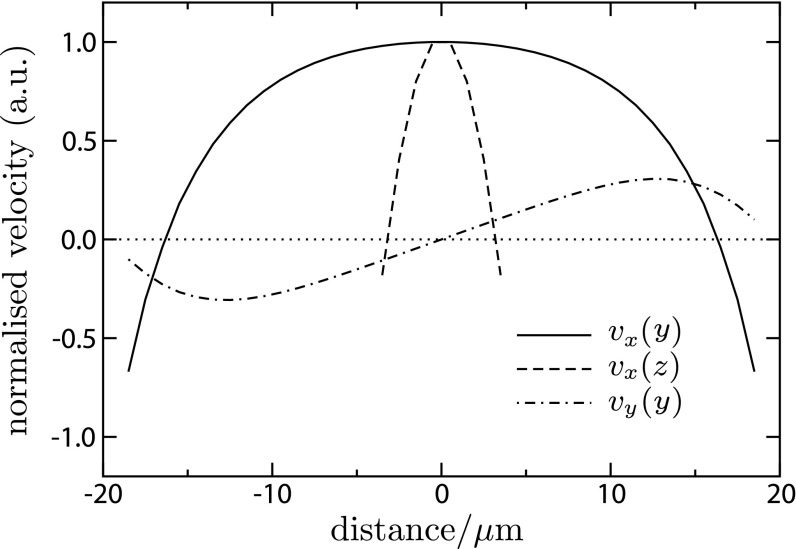
A representative section of the flow field near the entry to the capillary, at an early time Dst=1,600, is shown in Fig. S5. The flow profile in the vertical direction, vx(z), is close to a combination of plug flow and pure parabolic pressure-driven Poiseuille flow, which corresponds to our expectation from the lubrication flow in Eq. S9. However, the flow profile in the transverse direction, vx(y), is a blunted parabola, which is positive in the center and negative along the walls. The blunted shape arises from the additional friction due to the top and bottom walls. Our expectation is that this component of the flow is mainly responsible for the lateral curvature of the density profile of the colloid particles. Accompanying the longitudinal flow is a skew-symmetric lateral recirculation, vy(y), away from the centerline and toward the walls. This is the transverse analog of Eq. S10.

Fig. S5.

Fig. S5.

Representative flow field in capillary at x=15 μm from the open end and Dst=1,600 μm2 (i.e., 4Dst=80 μm). Shown is the longitudinal (vx) component of the flow field as a function of the distance from the center of the capillary in the transverse (y) and vertical (z) directions, and the transverse (vy) component in the transverse (y) direction.

Note that ∫vx dy is obviously nonzero in Fig. S5 because of the z dependence: it is only the total integrated longitudinal flow that should vanish, ∬vx dy dz=0 (this follows by integrating ∇⋅v=0 over a control volume that cuts the capillary in a plane normal to the longitudinal direction). We have checked that the LB flow field meets this test, or more precisely, since our LB is a compressible flow solver, we check that ∬ρ vx dy dz vanishes where ρ is the density (it was a failure of this test this that alerted us to the numerical problems with the moving-boundary link-bounce-back scheme).

Further Discussion on Additional Size Effects

Although there is a good agreement between the experiment and the theory when the finite Debye screening layer is fully taken into account, there still exists possible size-dependent phenomena worth mentioning. In what follows, we will discuss some of the possible phenomena that may exist.

Particle–Particle Interactions.

As the theory assumes an infinitely dilute medium, the first possible effect that comes to mind is the particle–particle interactions. This possibility occurs because the particle focusing is enhanced as the particle size becomes larger. Consider 2a≈1.01 μm diameter colloids for example: in bulk, the number density n of the particles is around 1 × 109/mL (or, 1 × 10−3 μm−3). Then, the packing fraction 4πa3n/3≈5 × 10−4 is very small. At a focusing ratio of 100, the number density n≈1011/mL (or 0.1 μm−3), and the subsequent packing fraction 4πa3n/3≈0.05, which is still very low.

As noted by Anderson (5), hydrodynamic interactions between particles undergoing phoretic motions are typically weak as long as the distance between the particles is much larger than the Debye layer thickness (which is in the order of 10 nm in our case). This is because the flow perturbation about a particle decays as r−3, where r is the distance away from the particle. Because the packing fraction of the particles, even at the maximum focusing ratio, is estimated as ≲0.05, hydrodynamic particle–particle interactions should be insignificant in our case.

Gravimetric Effects.

The density of the particles (polystyrene latex beads) is 1.05 g/mL, whereas the presence of NaCl at millimolar concentration makes negligible contribution to the solvent specific gravity. So the particles are mildly negatively buoyant (Δρ=0.05 g/mL). Then the scale heights for the particles, hs=kBT/(ΔρVg), where V is the volume of the particle and g is the gravitational constant, are estimated in Table S1. Because the height of the channel is 2h=10 μm, the scale height becomes comparable to the channel height for particle diameters ≳0.78 μm. The expected ratio in particle density between the top and the bottom of the channel is e−2h/hs, given as the third column in Table S1. Therefore, for 0.78- and 1.01- μm particles respectively, we estimate a 25% and 47% change in particle density in the vertical direction.

Table S1.

Properties of various polystyrene latex particles

Diameter (μm) hs (μm) exp(−2h/hs) Dp (μm2 s−1) vf,wallh/Dp h2/Dp (s)
0.06 87,100 0.99989 8.5 9 3
0.19 2,350 0.996 2.5 29 10
0.47 155 0.94 1.03 73 24
0.78 34.0 0.75 0.62 121 40
1.01 15.7 0.53 0.48 156 52

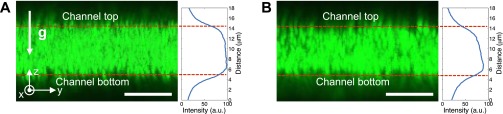
However, from the confocal microscope cross-sectional images of the particles inside a dead-end channel under stationary conditions (Fig. S6), the actual particle distribution is shown to be not as significant as what we have estimated: the particle density differences are measured as only of the order 4% and 15%, for 0.78- and 1.01-μm particles, respectively. We observe a noticeable wall-exclusion effect that effectively reduces the height of the channel, so that the actual particle density difference is smaller than the estimate.

Fig. S6.

Fig. S6.

Cross-section of dead-end channels filled with colloidal particles taken by confocal microscope (TCS SP5; Leica). Particle size: (A) 0.78 μm and (B) 1.01 μm; solution 0.02 mM NaCl. The particles were under stationary conditions. The final images are obtained by overlaying 300 consecutive images having time interval of 3 s. Line-averaged fluorescent intensity distribution, I(z)=∫I(y,z)dy along the vertical direction is also presented.

Wall Exclusion.

As the size of the particles become larger, wall exclusion becomes more important because the particle centers cannot approach the walls closer than the radius of the particle, a. Therefore, in a simplistic picture, the particles are more distributed within the middle portion of the circulating flow. This will tend to enhance the advective contribution to the particle migration, and will be an effect that increases as O(a/h) rather than the much sharper gravimetric effect. However, for the given dimensions a/h≲0.1, so we estimate that the wall-exclusion effect is on the order of 10% at maximum.

Electrokinetic Lift.

In the presence of particle motion near a charged wall, a so-called electrokinetic lift force (normal to the wall) arises due to the nonzero hydrodynamic stress within the gap between the particle and the wall (23). This force may give rise to an additional wall-exclusion effect so that the particles are more concentrated in the middle of the channel, where they experience the advective motion that gives rise to the particle migration toward the dead end. Our expectation is that electrokinetic lift operates only near the walls and could be captured by an additional wall-exclusion effect.

Hydrodynamic Dispersion.

Considering the detailed flow profile (e.g., Fig. S5), there could in principle be significant hydrodynamic dispersion effects arising both from particles diffusing across streamlines and from streamlines diverging due to the recirculating component of the flow. To get an idea of the potential importance of these effects in terms of size, we use the wall slip velocity vf,wall as the typical flow speed to calculate the Péclet number, vf,wallh/Dp, appropriate to dispersion in the vertical plane [because Γw≈210 μm2 s−1, and Δ(lnc)=ln100 over a distance of the order 100 μm, we have vf,wall=Γw ∂ln⁡c/∂x≈15 μm s−1]. The results (fifth column in Table S1) indicate that hydrodynamic dispersion is probably not negligible, and shows a strong size effect.

The full 2D simulation allows us to fully analyze the detailed particle dispersion dynamics over time and space, which is shown in Fig. S7. In the early stage, the particles migrate toward the wall because of the strong recirculating flow field that convects the particles. At the same time, particles are experiencing diffusiophoresis along the channel direction. The combination of these two components leads to accumulation of the particles near the wall, leading to lateral inhomogeneity of particle distribution. After the flow has weakened, the particles spread back to the center of the channel via Brownian motion. The time to diffuse back across the height h for different particles is given in the final column in Table S1. Owing to the size-dependent behavior of Brownian motion, the small particles diffuse back quickly whereas the large particles rather remain and maintain the lateral inhomogeneity. This lateral migration of the particles results in a broader particle distribution along with a slight lagging of the wave, which is clearly seen in Fig. S7. Clearly, however, this hydrodynamic dispersion lag can explain only a small fraction of the observed size dependence of the wave position.

Electrophoretic Contribution to Diffusiophoresis

Single Solute Diffusion.

In the presence of a solute gradient, by solving the Nernst–Planck equations for the cations and anions with a local charge neutrality approximation (37), we can obtain the spontaneous electric field arising from diffusion. The one-dimensional Nernst–Planck equations for cations (+) and anions (−) of charge q are given by

with

j±=−D±(∂c±∂x±c±qkBT∂ϕ∂x), [S13]

where j is the current and ϕ is the electrostatic potential. Assuming local charge neutrality by letting c+=c−=c, we get

and

j+=j−=j=−D+(∂c∂x+cqkBT∂ϕ∂x)=−D−(∂c∂x−cqkBT∂ϕ∂x) . [S15]

Solving these equations leads to the electric field as

E=−∂ϕ∂x=kBTq(D+−D−D++D−)∂ln⁡c∂x, [S16]

and c is obtained by solving the following diffusion equation

∂c∂t=2D+D−D++D−∂2c∂x2 . [S17]

The quantity 2D+D−/(D++D−)≡Ds is the ambipolar diffusion coefficient mentioned above.

Using D+=1.33 × 10−9 m2 s−1 for Na+, D+=1.96 × 10−9 m2 s−1 for K+, and D−=2.03 × 10−9 m2 s−1 for Cl− (24), we obtain an electric field of the order 50 and 4 V m−1 over a distance of the order 100 μm for NaCl and KCl, respectively. The ambipolar diffusion coefficient for NaCl is Ds=1.61 × 10−9 m2 s−1.

Multispecies Interdiffusion.

Likewise, a spontaneous electric field developed by interdiffusion of multiple species (NaCl and KCl) can also be estimated by solving the Nernst–Planck equations for cations (Na+ and K+) and anions (Cl−) with a local charge neutrality approximation. The Nernst–Planck equations for cations and anions are given by

∂cNa+∂t=−∂jNa+∂x=∂∂x(DNa+(∂cNa+∂x+cNa+qkBT∂ϕ∂x)) , [S18]
∂cK+∂t=−∂jK+∂x=∂∂x(DK+(∂cK+∂x+cK+qkBT∂ϕ∂x)) , [S19]
∂cCl−∂t=−∂jCl−∂x=∂∂x(DCl−(∂cCl−∂x−cCl−qkBT∂ϕ∂x)) . [S20]

Local charge neutrality is assumed by letting cCl−=cNa++cK+, so that we infer that the total current is conserved with net global current being zero, i.e., jCl−=jNa++jK+. A numerical calculation of these coupled equations with NaCl and KCl having equimolar concentration gives an electric field of the order 40 V m−1 over a distance of the order 100 μm, i.e., comparable to the NaCl case.

Supplementary Material

Supplementary File

Supplementary File

Supplementary File

Supplementary File

Supplementary File

Supplementary File

Acknowledgments

We thank Jie Feng for help with zeta potential and particle size measurements, and Janine Nunes, Orest Shardt, and Anne-Florence Bitbol for valuable discussions. We also thank the anonymous referees for valuable comments. We acknowledge Unilever Research for support.

Footnotes

Conflict of interest statement: P.B.W. discloses a substantive (>$10,000) stock holding in Unilever PLC.

This article is a PNAS Direct Submission.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary File

Supplementary File

Supplementary File

Supplementary File

Supplementary File

Supplementary File