The Matthew effect in science funding (original) (raw)

Significance

Why do scientists with similar backgrounds and abilities often end up achieving very different degrees of success? A classic explanation is that academic achievement exhibits a “Matthew effect”: Early successes increase future success chances. We analyze data from a large academic funding program that present a unique opportunity to quantify the Matthew effect and identify generative mechanisms. Our results show that winners just above the funding threshold accumulate more than twice as much funding during the subsequent eight years as nonwinners with near-identical review scores that fall just below the threshold. This effect is partly caused by nonwinners ceasing to compete for other funding opportunities, revealing a “participation” mechanism driving the Matthew effect.

Keywords: Matthew effect, cumulative advantage, science funding, regression discontinuity, sociology of science

Abstract

A classic thesis is that scientific achievement exhibits a “Matthew effect”: Scientists who have previously been successful are more likely to succeed again, producing increasing distinction. We investigate to what extent the Matthew effect drives the allocation of research funds. To this end, we assembled a dataset containing all review scores and funding decisions of grant proposals submitted by recent PhDs in a €2 billion granting program. Analyses of review scores reveal that early funding success introduces a growing rift, with winners just above the funding threshold accumulating more than twice as much research funding (€180,000) during the following eight years as nonwinners just below it. We find no evidence that winners’ improved funding chances in subsequent competitions are due to achievements enabled by the preceding grant, which suggests that early funding itself is an asset for acquiring later funding. Surprisingly, however, the emergent funding gap is partly created by applicants, who, after failing to win one grant, apply for another grant less often.

Why is academic success so unequally distributed across scientists? The theory of the Matthew effect identifies a self-reinforcing dynamic in academic stratification borne out of the tendency for a scientist’s past success to positively affect success in the future (1). The theory is that, if only one of two equally talented young scholars is given an award, the award-winning scholar will go on to have the more successful career. This happens because the winner enjoys resource and status advantages over the nonwinner (2–4). These advantages cause differences in future success to further grow, setting in motion a cumulative advantage process of increasing distinction (5–10). To the extent that luck plays a role in early academic success (11), the Matthew effect may undermine meritocracy by allowing an initially fortunate scientist’s recognition to self-perpetuate, while an equally talented but initially less fortunate counterpart remains underappreciated (1, 5–7).

An interdisciplinary literature finds patterns in observational data that are mostly consistent with the Matthew effect (7). Empirical testing of the Matthew effect, however, has been hampered by the possibility that observed cumulative differences in achievement are instead the gradual manifestation of unequal academic promise, which can only be imperfectly measured. While an empirical pattern of academic recognition repeatedly going to the same scientists is consistent with the Matthew effect, it is confounded with interpersonal differences in talent or productivity (12–19). Namely, increased differentiation in publication, citation, award, and employment records may point to endogenously emergent inequality (3, 20–25), but can also be interpreted as delayed revelation of variable ability or effort (5, 7, 10, 13). Measures of academic success follow extremely right-skewed distributions (20–22, 26–30), consistent with the Matthew effect thesis, but these may also reflect a convex correspondence between a scientist’s capability and repute, with only the very best receiving the lion’s share of recognition (5, 7, 8, 10, 18, 19, 31–34).

Our contribution is threefold: First, we address the causal inference problem using a regression-discontinuity approach. Second, we systematically study the Matthew effect in science funding, an important outcome that has received scant attention. And third, we identify a participation mechanism driving the Matthew effect whereby early stage failure inhibits participation in further competition through discouragement and lack of resources.

We argue that the Matthew effect may be particularly dominant in the accumulation of individual research funding. In contrast to scientists judging the quality of research papers, reviewers of grants, especially personal grants, are often explicitly tasked with evaluating the ability and promise of the applicant, using past achievements as criteria. The status mechanism theorized in earlier work, whereby past successes aid quality assessment under uncertainty, should thus be prominent in the allocation of research funds. In addition to status, grants provide a resource that can be invested to improve the quality of subsequent work (1, 24). Studying science funding also enables us to evaluate the proposed participation mechanism, whereby funding success promotes continued participation in future competitions for funding. This mechanism is particularly powerful in the earliest stages of the scientific career, when young scholars make defining career choices that largely depend on their prospects of acquiring permanent university positions. Winning an early grant will motivate scholars to compete for funding again if they suspect that their chances in future competitions have improved as a result.

Data

We perform a critical test of the Matthew effect in early career academic funding in The Netherlands. This empirical context provides an ideal research site. A single granting program, the Innovation Research Incentives Scheme, is the primary funding source for young Dutch scientists. Through this program, the Netherlands Organization of Scientific Research (NWO) has since 2000 concentrated €2,400,000,000 in the hands of a minority of 3,660 applicants with proposals deemed of superior promise. We exploit the feature of the program that funding decisions are made using a hard threshold in evaluation scores, with all winners having higher scores than all nonwinners. This policy makes a regression discontinuity design possible because differentiation among scores near the threshold can be considered “as good as random” (35). We isolate the effects of recent PhDs winning an early career “Veni” grant by comparing the subsequent funding success of nonwinners with evaluation scores just below the threshold to winners with scores just above it. An additional advantage of this research site is that data on applicants in the midcareer “Vidi” competition allow us to assess whether improved rates of success among winners of earlier grants in later contests result from increased participation in these contests. Since the data track many careers for over a decade, we can evaluate the cumulative impact of early career success.

Results

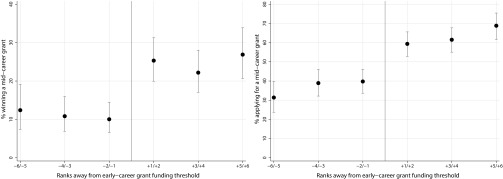
To identify the effect of winning an early career grant on winning a midcareer grant, we calculate the percentage of midcareer grant winners among early career grant applicants at different ranks away from the early career funding threshold (Fig. 1, Left). Those who won an early career award by the smallest margin (+1/+2) are roughly two-and-a-half times more likely to win a midcareer award than those who fell just short of winning an early career award (−1/−2) (exact test, P < 0.001). Parametric estimation (SI Appendix) identifies an effect of the same magnitude and significance. Midcareer award chances do not differ between any other pair of neighboring ranks of applicants in the early career competition, suggesting that this cumulative advantage effect does not spuriously reflect superior proposal quality or scientific ability. The effect is found for both women and men and is robust across academic fields (SI Appendix).

Fig. 1.

Fig. 1.

Effect of an early career grant on winning a midcareer grant (Left) and on applying for a midcareer grant (Right). Shown is the percentage of early career grant applicants winning a midcareer grant (Left, vertical axis) and applying for a midcareer grant (Right, vertical axis) for different evaluation ranks of applicants in the early career grant competition (horizontal axis). Applicants with positive ranks (+) to the right of the funding threshold (vertical line) received an early career grant, while applicants with negative ranks (−) did not. For each estimate, an exact 95% confidence interval is displayed.

To test the presence of the proposed participation mechanism, we calculate the probability that early career grant applicants of different application ranks submit a proposal to the midcareer competition (Fig. 1, Right). We find no significant difference between neighboring pairs of ranks in the probability of applying for a midcareer grant except between winners and nonwinners closest to the threshold (exact test, P < 0.001). Thus, a substantial portion of the increase in the probability of winning a midcareer grant from 10 to 26% resulting from winning an early career grant (Fig. 1, Left) can be accounted for by an increase from 40 to 59% in application chances (Fig. 1, Right). Supplementary analyses reveal that these differences in application chances are not caused by nonwinners exiting academia or moving to another country (SI Appendix), but rather by their decisions to not partake in later competitions.

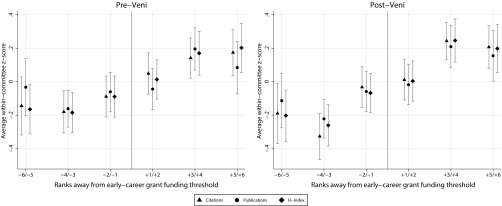
To test whether the observed positive effects on winning a midcareer grant (Fig. 1, Left) can be attributed to increased impact of scholarly work enabled by the early career grant, we compare the number of publications, citations, and H-index of early career applicants of different ranks (Fig. 2). Consistent with prior research (36–38), we find a positive association between ranking in the early career competition and each of the impact measures both before and after the competition. However, none of the impact measures exhibit a discontinuous increase at the cutoff, and the relationship between competition rank and productive achievement is the same before as after the award competition. This finding indicates that the early career grant does not raise measurable dimensions of scientific output (see SI Appendix for analyses further corroborating this conclusion) and therefore does not suggest that winners of early career grants in later competitions are better evaluated than nonwinners for having achieved greater scientific impact as a result of the earlier grant. This result is consistent with the status mechanism proposed in earlier work (1, 24, 25), whereby the improved success chances would be attributable to recognition for having won the early career grant. It is also possible that time and resources made available by the early career grant allow winners to write a higher quality proposal for the midcareer competition.

Fig. 2.

Fig. 2.

Scientific impact before (Left) and after (Right) early career grant competition by ranking. Shown are three measures of scientific impact (vertical axis), the average standardized number of citations (triangles), publications (dots), and H-index (diamonds) for different evaluation ranks of applicants (horizontal axis). Applicants with positive ranks (+) to the right of the funding threshold (vertical line) received an early career grant, while applicants with negative ranks (−) did not. For each estimate, a normal 95% confidence interval is displayed.

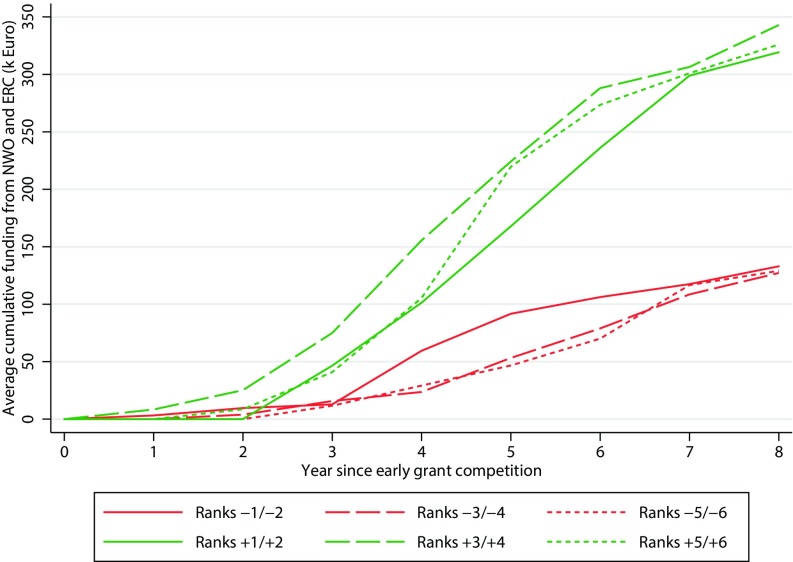
To calculate the long-term impact of winning an early career grant on funding success, we pool the scientists’ overall success in four major grant competitions: the NWO Vidi grant (maximum €800,000), the NWO Vici grant (maximum €1,500,000), the European Research Council (ERC) Starting grant (maximum €1,500,000), and the ERC Consolidator grant (maximum €2,000,000). Consistent with the Matthew effect thesis, we find that the head start given to early career grantees produces a widening gap with nongrantees (Fig. 3). After 4 y, the lowest-ranked winners (+1/+2) have received, on average, €40,000 more in research funding than the best nonwinners (−1/−2) (rank-sum test; P < 0.01), and this difference grows to approximately €180,000 after 8 y (rank-sum test, P < 0.01). Over the entire period the lowest-ranked winners in the early career competition accumulated more than twice as much grant money as the highest-ranked nonwinners, excluding the €250,000 early career grant itself. This gap chiefly reflects differences in funding probabilities, as we find the Euro amounts of later awards received by early career grant winners to equal those of nonwinners (SI Appendix). In stark contrast, winners with neighboring evaluation ranks do not significantly differ from one another in later funding success, nor do nonwinners with neighboring ranks, suggesting that later-stage funding differences between early career grant winners and nonwinners near the funding threshold are not attributable to differences in these scientists’ abilities. The emergent funding gap (€180,000) accounts for 40% of the entire difference in accumulated earnings between the best and worst applicant (€450,000) (SI Appendix), suggesting that the Matthew effect plays a dominant role in the creation of funding inequality.

Fig. 3.

Fig. 3.

Accumulation of grant money by early career grant applicants. Shown is the cumulative amount of funding received in NWO and ERC competitions (vertical axis) as a function of the number of years elapsed since the early career grant competition (horizontal axis). This relationship is shown for different ranks above (green, +) and below (red, −) the early career funding threshold.

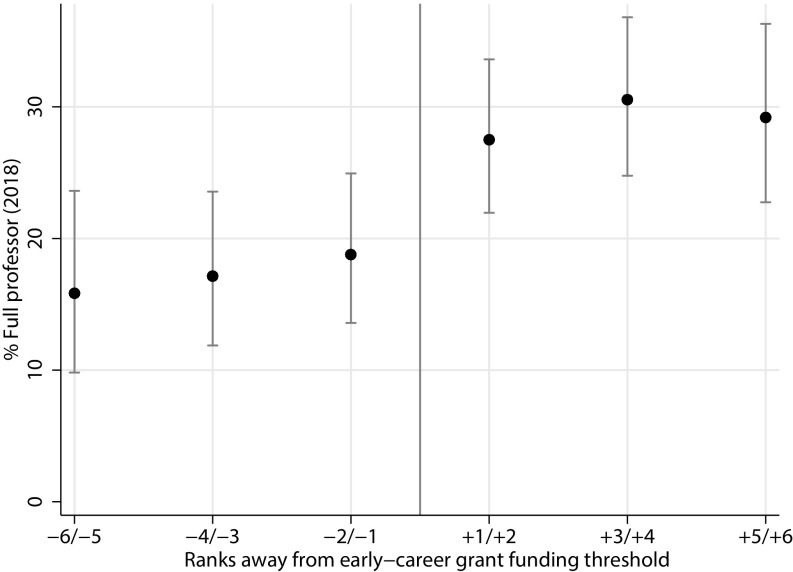
Finally, we explore the possibility that early career grants sort winners into more successful academic career tracks than nonwinners. In Fig. 4, we find that being awarded an early career grant raises long-term prospects of a full professorship by 47% [i.e., from 19 to 28% (P < 0.05)]. This result confirms that the award competition not only produces an enduring rift in funding success, but also has a lasting impact on winners’ and nonwinners’ positions in the academic hierarchy.

Fig. 4.

Fig. 4.

Effect of an early career grant on being full professor 10–16 y later. Shown is the probability of holding a professorship in 2018 (vertical axis) for different evaluation ranks of applicants in the early career grant competition (horizontal axis). Applicants with positive ranks (+) to the right of the funding threshold (vertical line) received an early career grant, while applicants with negative ranks (−) did not. For each estimate, an exact 95% confidence interval is displayed.

Discussion

We conclude that funding of early career scientists exhibits a Matthew effect that operates through two mutually reinforcing processes: On the demand side, candidates who won prior awards are evaluated more positively than nonwinners, while on the supply side, scientists who were successful in past contests select themselves into applicant pools of subsequent contests at higher rates than unsuccessful scientists.

The key institutional features of the Dutch academic funding system that enable the observed demand-side dynamics are widespread in grant competitions elsewhere, which suggest that the positive feedback effect uncovered here is likely to extend to other contexts. Prior academic success is often a merit review criterion, investigators are often unlimited in the number of grants they can pursue, and information about an applicant’s past grants is often available for consideration by reviewers, panelists, and program directors. Our results thus raise the question of whether funding organizations worldwide should change the common practice of providing information on prior awards and other investigator success metrics to evaluators of applications.

The observed tendency for winners of earlier grants to try their luck in later competitions in greater numbers than nonwinners suggests that funding agencies could consider outreach efforts aimed at reducing this gap. One costless measure that agencies may take is providing unsuccessful applicants with detailed information on how close evaluation scores were to the funding threshold, which may prevent near-winners with good past proposals from concluding that future odds are too low for investing time and effort in a new application.

Recent studies have documented rising inequality among scientists across the academic world (38, 39). Not only do our findings suggest that positive feedback in funding may be a key mechanism through which money is increasingly concentrated in the hands of a few extremely successful scholars, but also that the origins of emergent distinction in scientists’ careers may be of an arbitrary nature. This raises the question of whether, especially in fields where materials and infrastructure costs are modest, the distribution of smaller grants across a larger number of scientists could reduce inequality and improve meritocracy without sacrificing efficiency.

Supplementary Material

Supplementary File

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission. C.W. is a guest editor invited by the Editorial Board.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary File