Priority Effects and Nonhierarchical Competition Shape Species Composition in a Complex Grassland Community (original) (raw)
. Author manuscript; available in PMC: 2021 Oct 15.
Published in final edited form as: Am Nat. 2019 Jan 10;193(2):213–226. doi: 10.1086/701434
Abstract
Niche and fitness differences control the outcome of competition, but determining their relative importance in invaded communities—which may be far from equilibrium—remains a pressing concern. Moreover, it is unclear whether classic approaches for studying competition, which were developed predominantly for pairs of interacting species, will fully capture dynamics in complex species assemblages. We parameterized a population-dynamic model using competition experiments of two native and three exotic species from a grassland community. We found evidence for minimal fitness differences or niche differences between the native species, leading to slow replacement dynamics and priority effects, but large fitness advantages allowed exotics to unconditionally invade natives. Priority effects driven by strong interspecific competition between exotic species drove single-species dominance by one of two exotic species in 80% of model outcomes, while a complex mixture of nonhierarchical competition and coexistence between native and exotic species occurred in the remaining 20%. Fungal infection, a commonly hypothesized coexistence mechanism, had weak fitness effects and is unlikely to substantially affect coexistence. In contrast to previous work on pairwise outcomes in largely native-dominated communities, our work supports a role for nearly neutral dynamics and priority effects as drivers of species composition in invaded communities.
Keywords: competition, invasion, coexistence, communities, disease ecology
Introduction
Understanding the long-term outcome of competition in diverse species assemblages is a major goal of ecology, but measuring outcomes empirically is often infeasible when dynamics proceed slowly relative to the timescale of experiments. Theoretical coexistence models based on species differences offer a powerful alternative for predicting competitive outcomes (Burdon and Chilvers 1974; Tilman 1980; Holt et al. 1994). However, linking models to real ecological communities is challenging because realistic parameter estimates are rarely available for species interacting within a single ecological context. Moreover, existing theoretical approaches often make simplifying assumptions—such as reducing analyses to pairs of interacting species rather than considering the full dynamics of the assemblage—that may affect the inferred outcomes. As a result, considerable uncertainty remains about the relative importance of different proposed diversity-maintenance mechanisms, and the outcome of competition can be difficult to predict.
Among several existing theoretical frameworks for species interactions, modern coexistence theory clarifies the mechanisms through which species differences affect the outcome of competition via their effects on niche differences and fitness differences (Chesson 2000). Niche differences are the differences between species in resource use, natural enemies, habitat requirements, or other factors that force per capita impacts of competition within species to exceed those between species (Chesson 2000). These niche differences cause population growth to be negatively frequency dependent because species achieve their highest per capita growth rates when they are rare and interact with mostly heterospecific competitors, while per capita growth declines as species become common and interact with many conspecific competitors. By contrast, in this framework, fitness differences are those differences between species that determine per capita growth rates independent of relative abundance, often including differences in fecundity, resource acquisition, or survival. Coexistence occurs when niche differences, which generate negative frequency-dependent population growth or stabilization, are strong enough to overcome fitness differences between species (Chesson 2000). Alternatively, priority effects can occur when population growth is positively frequency dependent, allowing any species that is initially more common to exclude others but preventing species from invading when rare in the presence of competitors (Mordecai 2011; Fukami et al. 2016). While assessing competitive outcomes in pairs of species with known parameter values is straightforward in this framework, predicting multispecies outcomes remains a challenge (Saavedra et al. 2017; Barabás et al. 2018).
Modern coexistence theory has motivated a suite of studies that empirically measure the strength of niche differences and fitness differences—and, ultimately, the outcome of competition—in natural plant or algal communities. Many of these studies have emphasized the influence of stabilizing niche differences on species coexistence (Turnbull et al. 2005; Adler et al. 2006, 2010; Levine and HilleRisLambers 2009; Narwani et al. 2013; Godoy et al. 2014, 2017; Kraft et al. 2015). However, almost all empirical applications of modern coexistence theory use pairwise growth rates when rare to assess community-wide outcomes (e.g., Adler et al. 2007, 2010; Levine and HilleRisLambers 2009; HilleRisLambers et al. 2012; Mordecai 2013; Godoy et al. 2014; Kraft et al. 2015; Mordecai et al. 2015). A growing body of theory shows that outcomes of competition may depart from pairwise predictions when all species are analyzed simultaneously (e.g., Case 1995; Allesina and Levine 2011; Mayfield and Stouffer 2017; Saavedra et al. 2017) and that even two-species models can depart from the predictions of invasion analyses in some settings (Barabás et al. 2018). Deviations from pairwise predictions may originate from indirect effects on competitor density; nonhierarchical interactions, in which competitive impacts are intransitive; or higher-order interactions, in which the per capita impact of one species on another is mediated by interactions with a third species. In complex communities, it is theoretically possible to observe priority effects within groups of species with high niche overlap and fitness similarity, which occur alongside deterministic coexistence or competitive exclusion between groups of species with larger niche differences and fitness differences. Despite these theoretical developments, there are few empirical examples of communities in which multispecies outcomes depart from two-species predictions (but see Godoy et al. 2017; Mayfield and Stouffer 2017), although alternative stable states have been empirically documented outside the coexistence literature (Fukami et al. 2005; Carpenter et al. 2011; Staver et al. 2011). It is unknown whether departures between pairwise and multispecies predictions are a common biological phenomenon or a quirk of mathematical models. Moreover, it is not clear how ecological contexts—such as the coevolutionary history of the competing species and the level of disturbance—may influence the likelihood of complex multispecies dynamics as compared to negative frequency-dependent stabilization (Ocampo-Ariza et al. 2018).
We hypothesized that complex multispecies dynamics would be likely to emerge in recently invaded systems, in which competing species have not had long coevolutionary histories and hence may not have had sufficient time to evolve into distinct niches (MacDougall et al. 2009). Such systems may be far from equilibrium and may represent an opportunity to study complex multispecies dynamics in the absence of strong stabilizing mechanisms driven by niche differentiation. Moreover, predicting competitive outcomes in recently invaded systems is a pressing concern for conservation, and understanding the processes that have the largest impact on the persistence of native species could help preserve endemic biodiversity. In this study, we investigated competitive outcomes in California grasslands, one of the most ecologically important and widespread ecosystems in the Western United States and a key reservoir of endemic biodiversity (Myers et al. 2000). Simultaneously, California grasslands are heavily invaded and human impacted since the nineteenth century (Mack 1989); exotic annual grasses now dominate, while native perennial bunchgrasses and annual forbs have declined to very low density throughout much of their extent. In the long term, it is not clear whether the exotic annual grasses will competitively exclude native perennial grasses, whether native grasses will stably persist (at reduced densities), or whether priority effects will determine whether native or exotic grasses dominate at a local scale.
Here we combine field experiments with mathematical models to predict the outcome of competition in a community of five co-occurring native and exotic grasses in a grassland ecosystem. We develop and empirically parameterize population-dynamic models for the species in this complex community. The models incorporate a suite of demographic rates experimentally measured for three different exotic annual grasses and two native perennial grasses at a single Northern California grassland site and include the impact of fungal pathogens on those demographic rates, which may affect competitive outcomes by altering fitness differences or by inducing negative frequency dependence of growth rates (Mordecai 2011, 2013). We estimate parameters of the model statistically from field observations of seed output, germination, establishment, seed infection, and adult survival for each of five competing species of exotic annual and native perennial grasses. Using the parameterized model, we study the multispecies outcome of competition, with and without pathogens. Specifically, we ask the following questions: (1) How strong are intra- and interspecific competition between native and exotic grass species? (2) What is the predicted outcome of competition? (3) Do complex outcomes, including priority effects and/or intransitive competition, emerge from the dynamics of the full multispecies assemblage? (4) How strongly do foliar and seed pathogen impacts on demographic rates influence the outcome of competition?
Methods
Empirical Data Collection and Parameter Estimation
Study System.
We chose five focal species that are highly abundant and widespread in California grasslands: exotic annual grasses Avena barbata, Bromus diandrus, and Bromus hordeaceus and native perennial bunchgrasses Stipa pulchra and Elymus glaucus. For each species, we measured a full complement of demographic rates that determine population growth: seed germination, seedling establishment, the impact of competition on per capita seed production, and over-summer survival (for both seedling and adult perennial bunchgrasses). We also assessed seed infection and survival with a common fungal pathogen that causes a disease called black fingers of death, which can kill native and exotic grass seeds (Beckstead et al. 2010). All experimental work was conducted in Jasper Ridge Biological Preserve, located in San Mateo County, California (37°24′N, 122°13′30″W; 66–207 m). This 485-hectare biological preserve is managed by Stanford University and has a Mediterranean climate, with cool, wet winters and warm, dry summers (mean annual precipitation = 622.5 mm; Ackerly et al. 2002). All demographic rates (except the perennial seedling-to-adult-transition probability; see below) were measured in winter 2015 to spring 2016 (the 2016 growing season), an average rainfall year with 601 mm total precipitation distributed over 20 precipitation events.
Competition Experiment and Transect Sampling.
Seed output is an important component of plant reproduction and is strongly impacted by competitor density for many plants (Mordecai 2013; Mordecai et al. 2015). We measured seed output as a function of competitor density by varying the density of each plant species in monoculture and in mixed-species plots and measuring per capita impact on seed production for each competitor species (Levine and HilleRisLambers 2009; Mordecai 2013). The 1-m2 competition plots were randomly assigned to five competitor density treatments, ranging from 10% to 100% of each species’ estimated natural density in monoculture, for each of the seven background species groups (respective seedlings of A. barbata, B. diandrus, B. hordeaceus, and E. glaucus; E. glaucus adults; S. pulchra seedlings; and S. pulchra adults). We also cleared 4-m2 plots of competitors to measure seed output on individuals of each species at low competitor density (though natural recruitment from the seed bank meant that these plots were not completely clear of competition). We used weed matting, weeding, and seed addition to manipulate competitor densities. At the end of the 2016 growing season, we measured seed output from up to three focal plants per species per plot (as available). See the appendix, available online, for a complete description of the competition experiment.
We also measured the impacts of competition on seed production in six transects that naturally varied in plant composition. Each transect varied in grass composition from native perennial dominated at one end to exotic annual dominated at the other, with five 1-m2 plots spanning each transect spaced approximately 5–10 m apart. For each focal plant in the transects, we estimated seed output in both the 2015 and 2016 growing seasons (see appendix).
To assess pathogen damage and its relationship with seed production and competitor density, we visually estimated leaf area damaged by fungal infection on a subset of leaves on each focal plant in both the transects and experimental plots. We used these data to quantify the impact of foliar fungal infection on seed output, as well as the impact of plant species’ local relative abundance on pathogen damage. We note that this approach could underestimate the impact of fungal infection if resistance is generally costly, and most surveyed plants were actively fighting infections.
Our attempt to manipulate competitor densities in the experimental plots was only partially successful because of recruitment from the seed bank. As a result, we combined all focal plants into a single data set of seed outputs and observed competitor densities (rather than using the target densities for the experimental plots). Our final data set included 439 A. barbata, 399 B. hordeaceus, 319 B. diandrus, 387 S. pulchra, and 234 E. glaucus individuals (see appendix for further details).
We used Markov chain Monte Carlo (MCMC) to infer parameters relevant to seed output (λ), competition (α), and foliar infection (β) from our competition experiment data (see “Population-Dynamic Model” and table 1 for parameter definitions) and performed simulation-based validation of our estimation procedure. Full details of this estimation procedure and its validation are provided in the appendix, along with a more detailed description of the experimental design. We repeated the parameter inference procedures on subsets of the data that included either only the experimental plots or only the transects and found that parameter values were of similar magnitude and with overlapping posterior distributions (see fig. A7 and appendix; figs. A1–A8 are available online).
Table 1:
Descriptions of parameters and variables relevant to our population-dynamic model
| Parameters/variables | Description |
|---|---|
| αjl | Per capita competition impact of species l on species j |
| βj | Impact of foliar fungal infection per unit area infected |
| Aj | Mean leaf area infected |
| λj | Mean seed output in the absence of infection and competition |
| fj(t) | Compound impact of competition and infection on seed output |
| Sj | Seed output after accounting for competition and infection |
| gj | Germination fraction |
| γj | Seed survival rate in presence of BFOD pathogen |
| νj | Seedling survival rate |
| ϕjI | Establishment probability for infected seedlings |
| ϕjU | Establishment probability for uninfected seedlings |
| Dl | Density of competitor species l per m2 |
| νj0 | Seedling transition rate in the absence of competition |
| νj(t) | Seedling transition rate after accounting for competition |
| αs | Impact of seedlings on seedling-adult transition |
| αa | Impact of perennials on seedling-adult transition |
| αn | Impact of exotic annuals on seedling-adult transition |
| Ds | Density of seedlings per m2 |
| Da | Density of exotic annuals per m2 |
| Dn | Density of perennials per m2 |
| PjI | Proportion of seedlings infected during seedling-adult transition |
| ξj | Rate of perennial adult over-summer survival |
| nja(t) | No. annual seeds at time t |
| njp(t) | No. perennial seeds at time t |
| aj(t) | No. perennial adults at time t |
Germination Data.
We planted marked seeds of each focal species to track germination and seedling establishment in 30 plots of 25 individuals of each species in November 2015. We recorded their status weekly for 4 weeks in January and February as missing (M), alive (A), or alive with >50% of leaf area with pathogen damage (P). We used a Markov model to estimate the probability of establishing, surviving, and becoming heavily infected for each species by calculating weekly transition probabilities between these three states by plant species and then using the matrix to project forward 4 weeks to estimate the overall probability of germinating and establishing. We repeated this calculation both with pathogens present and with pathogens removed (i.e., as if all individuals experienced the establishment rates of uninfected individuals) in order to understand the impact of pathogens on seedling establishment (fig. A1 shows inferred germination gj and establishment ϕjU and ϕjI for uninfected and infected individuals, respectively, for each species j).
Seed Survival and Infection Data.
Seeds that remain dormant in the seed bank may contribute to population growth when they germinate in future years. To assess survival of nongerminating seeds between years, we buried 30 mesh seed bags containing five sewn compartments of 100 seeds of each focal plant species 2–5 inches deep from November 2015 through July 2016. We retrieved all intact seeds and scored them for black fingers of death (BFOD) pathogen damage (Beckstead et al. 2010; Mordecai 2013), which is likely caused by one of the numerous Pyrenophora species that are common in these sites (Spear and Mordecai 2018). We tested all intact, nongerminated seeds for viability using germinatino, gibberellic acid, and cut tests, as in previous work (Mordecai 2012). We parameterize the fraction of seeds killed from BFOD infection as γj for species j (fig. A2).
Adult Survival Data.
To assess the survival of S. pulchra and E. glaucus, we marked 200 adult perennial bunchgrasses with flags in June 2015 at four sites for each species and revisited prior to senescence in June 2016. We recovered 167 S. pulchra and 170 E. glaucus flags on the second visit and recorded them alive or dead based on observing green tissue and/or new fruiting stalks. We fit binomially distributed models of survival probability for each species using beta-distributed priors with parameters α = 1 and β = 1 (fig. A3).
Perennial Transition from Seedling to Adult.
We modeled perennial seedling over-summer survival as a function of competitor density and per capita competitive effects using data and fitted parameters from previously published work (Mordecai et al. 2015). Briefly, we modeled perennial seedling over-summer survival as a beta-binomially distributed process where for each observation k, the number of surviving seedlings maturing into adulthood was
| Yk∼beta binomial(d,d(1−μk)μk,nk), | (1) |
|---|
where μk = ν/1 + ∑k αjDkj is the expected value over all competitor species j. Here ν is the per capita survival probability in the absence of competition, αj is the per capita competitive effects of individuals of species j, and Dkj is the number of individuals of species j in observation k. In the beta-binomial distribution, d affects the mean and variance, and nk is the number of trials in observation k. The equation for Yk is parameterized so that its mean is equal to μk. Since we lacked the data to separately estimate αj for each individual species in our sample, we estimated an αj for perennial adults, perennial seedlings, and exotic annuals, respectively.
Population-Dynamic Model
Model Structure.
We developed a dynamic model that captures the effects of competition and fungal infection on growth rates for each grass species in our system, which is structurally similar to models developed in previous work (Mordecai 2013; Mordecai et al. 2015). All parameters and variables in the population-dynamic model are listed in table 1. To model the effects of competition on the population growth of each species, we suppose that each plant of species j has a seed output of λj in the absence of competition and that competition and infection reduce seed output by
| fj(t)=11+(∑lαjlDl(t))+Ajβj, | (2) |
|---|
where Dl(t) is the density of competitor species l per square meter at time t and Aj is the mean leaf area that was infected on individuals of species j. The expected seed output of a single individual Sj(t) is then
In the absence of transmission information, we do not explicitly model transmission of fungal pathogens but simply assume that each individual is infected at the mean level of observed foliar fungal infection for species j.
For each species j, we suppose that a fraction gj of the seeds germinate, and among these a fraction γj are infected with a fungal seed pathogen (BFOD). Seeds that germinate and are not infected may then establish or maybe eliminated before they ever produce seeds. We supposed that the probability of establishment depends on foliar fungal infection status and separately estimated the probability of establishment for infected (ϕjI) and uninfected (ϕjU) seedlings for each species j. The proportion of seedlings that are infected during the transition is given by PjI.
Perennial seedlings are presumed to be weak competitors and are not included in the competition model and produce no seeds in the first year of life (Mordecai et al. 2015) but are subject to competition in their survival over their first summer. Perennial seedlings survive at rate νj(t), given by
| νj(t)=νj01+αsDs(t)+αaDa(t)+αnDn(t), | (4) |
|---|
where D is the density of competitors; the subscripts s, a, and n represent perennial seedlings, perennial adults, and annuals, respectively; and νj0 is the survival rate in the absence of competition. For this aspect of the model, we group all annual and perennial plants together instead of computing each species competitive effect separately because we lacked the data necessary to infer the parameters for each species individually. Perennial seedlings that survive the summer then become adults in the following year. Perennial adults are also subject to over-summer mortality at rate (1 − ξj), modeled as competition independent because deaths of adult bunchgrasses are relatively rare (fig. A3).
We model germination rate Gj after accounting for infection and establishment (see “Seed Survival and Infection Data”) with
| Gj=gj(1−γj)(ϕjU(1−PjI)+ϕjIPjI). | (5) |
|---|
Additionally, we suppose that the proportion of seeds remaining in the seed bank after germination and infection Bj is given by
At each time step, for each species j, we track the number of seeds nja(t) for exotic annuals or the number of seeds njp(t) and adults aj(t) for perennials. Combining across seed production, competition, foliar fungal infection, fungal seed infection, germination, establishment, and over-summer survival, the full population growth equations are
| nja(t+1)=nja(t)(Gjλjfj(t)+Bj), | (7) |
|---|
| njp(t+1)=aj(t)λjfj(t)+njp(t)Bj, | (8) |
|---|
| aj(t+1)=aj(t)ξj+njp(t)Gjνj(t). | (9) |
|---|
The germination, adult survival, seed infection, and seedling transition parameters were estimated as described in the previous sections. The competition (α), seed output (λ), and foliar infection burden (β) were estimated using custom MCMC software, as described in the appendix. Simulations of each species in monoculture show a strong positive correlation with observed monoculture densities in the field (fig. A6), suggesting that our model parameterization with independently measured demographic rates accurately describes the system.
Separating Infectious Processes from Competition.
Initially, we considered three broad classes of models that (1) did not include the impacts of infection, (2) included only foliar infection, and (3) included both foliar infection and BFOD pathogen. Since foliar infection had a negligible impact on dynamics and competitive outcomes, we compare models that include only foliar fungal infection to models that include both foliar infection and BFOD. The foliar infection model includes both the parameters relevant to infection of perennial seedlings during their transition to adults and infection of leaves of adult perennials and exotic annuals.
Inferring the Outcome of Competition.
We used the parameterized models to investigate the outcome of competition using both pairwise and multispecies approaches to assess any differences in the outcome across approaches and to understand potentially complex outcomes more mechanistically. First, we used the posterior parameter estimates and the population-dynamic model to compute growth rate when rare (GRWR) for each pair of species. If in a pair of species each has GRWR > 1 (i.e., log(GRWR) > 0, where log is the natural logarithm), then stable coexistence is predicted because the rarer species is expected to increase in prevalence, preventing either species from being excluded (Turelli 1978; but see Case 1995). Pairwise competition calculations were performed in the presence of fungal infection (i.e., including all model parameters pertinent to foliar or seed fungal infection).
To calculate GRWR for each species pair, we sampled the relevant demographic rate parameters from their posterior distributions and simulated one species forward to its stable monoculture density; from there, we computed the growth rate of an invader of another species. For perennials, we computed GRWR as the dominant eigenvalue of the 2 × 2 matrix describing the rate of transition between seed and adult stages, which accounts for their stage-structured life history (Mordecai 2013). For exotic annuals, we calculated GRWR by simulating the addition of a single individual to the monoculture species and calculating the growth rate in the second generation. We also calculated percent difference in GRWR (pdGRWR) as 100(1 – A/B), where B is the GRWR in an empty plot and A is the GRWR under invasion conditions.
Second, we investigated competitive outcomes for the full species assemblage using simulations. Because outcomes could be initial condition dependent, we initialized our simulations at a range of observed densities from the transects. We simulated 600 years and report results of species mixtures at this time point (Mordecai 2013). For species that were not present in a sampled transect, we introduced a pseudo-count of one individual so that each species is initially present in each simulation. We consider species with population sizes exceeding one individual at the end of the simulation to have persisted, while species with less than one individual are excluded.
Last, we performed invasion experiments to better understand the dynamics underlying some of the coexistence outcomes that were predicted under our model. In these experiments, we compared the ability of E. glaucus to invade established S. pulchra plots with and without the presence of an exotic annual competitor. We considered only the subset of posterior parameter estimates in which S. pulchra was predicted to coexist with B. diandrus, excluding all replicates in which single species dominance was predicted. We simulated 100 years of S. pulchra growth in the absence of competitors to allow it to establish. Subsequently, at time t = 100, we either invaded B. diandrus or allowed S. pulchra to continue in the absence of competitors for another 100 years, and finally we introduced a single E. glaucus individual at time t = 200. We summarized these experiments by calculating the proportion of posterior samples in which S. pulchra is able to prevent E. glaucus from invading after 600 simulated years post-invasion. We sampled one set of parameters randomly from among the posterior estimates to display this invasion experiment, but note that we vary the timing of the invasions for the purpose of visualization (fig. 4).
Figure 4:
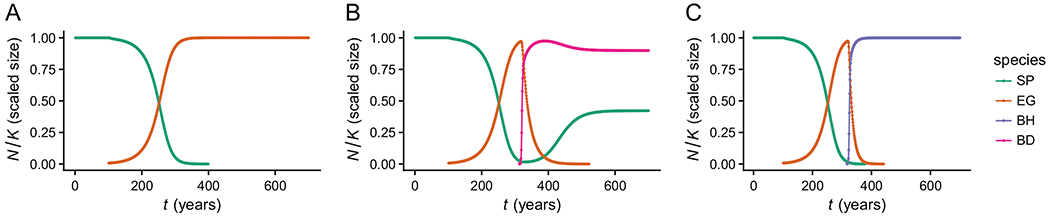
Effect of exotic annuals on invasion dynamics. Panels A–C correspond to a single set of parameter estimates sampled from the posterior distribution. A, Elymus glaucus (EG) invades at t = 100 and is able to establish and eventually replace Stipa pulchra (SP). B, EG invades at t = 100 and is able to establish and gradually replace SP. Bromus diandrus (BD) invades at t = 220 and coexists with SP, reversing the invasion of EG and preventing EG and Bromus hordeaceus (BH) from invading in the future. C, EG invades at t = 100 and is able to establish and gradually replace SP. BH invades at t = 220 and outcompetes both perennials. BD cannot invade due to the priority effect between BD and BH. Units on the _Y_-axis correspond to population sizes relative to monoculture density Perennial native species: S. pulchra, E. glaucus; annual exotic species: B. hordeaceus, B. diandrus. Priority effects occur when the probability of persistence depends strongly on initial density.
Results
Evidence for Strong Interspecies Competition
We calculated the pairwise log(GRWR), where zero is the threshold for invasion, of each species invading a monoculture of each other species to assess the pairwise outcomes of competition (fig. 1A). We also calculated the proportional decrease in GRWR relative to the growth rate in the absence of competition to assess the overall impact of competition on population growth (pdGRWR; fig. 1B). The values plotted in figure 1 represent the mean over 250 independent samples of the parameters from their posterior distribution. If there were strong niche differences between all pairs of species, each species would strongly constrain its own growth rate but have a relatively weak competitive impact on other species. By contrast, we observed high niche overlap in this system, in which interspecific competition constrains invasion growth rates as much or more than intraspecific competition (fig. 1A). Along the diagonal, where each species competes with itself at its stable monoculture density, the log(GRWR) was always very near zero (fig. 1A). When the native perennial species (Elymus glaucus and Stipa pulchra) were the invaders, they were constrained to log growth rates close to zero by all competitors except Avena barbata, which is unable to constrain either species. By contrast, neither perennial species reduced the log(GRWR) of any of the annual species to below zero. Bromus hordeaceus and Bromus diandrus tightly constrained each others’ growth rates but were not strongly constrained by the perennial competitors. Avena barbata was a poor competitor in this community and only constrained itself while being tightly constrained by both of its annual competitors.
Figure 1:
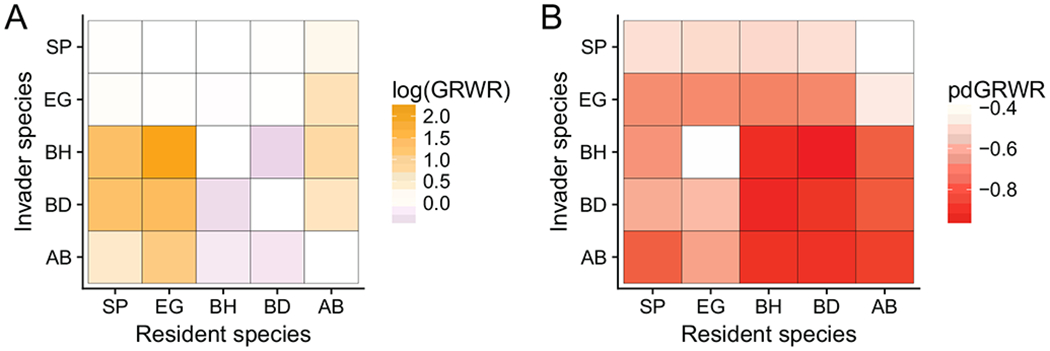
Strength of pairwise competition inferred from the growth rates of invaders introduced at low density to established monocultures of residents. A, Log of growth rate when rare (GRWR) – log(GRWR) > 0 is the invasion criterion. Larger positive values (darker yellow/orange) represent high niche overlap, while darker purple represents less overlap. B, The proportional difference in each species growth rate in the presence of the resident species as compared to its growth rate in the absence of competition. Perennial native species: Stipa pulchra (SP), Elymus glaucus (EG); annual exotic species: Bromus hordeaceus (BH), Bromus diandrus (BD), Avena barbata (AB).
These results are not driven solely by some species having low overall (competition-independent) growth rates, because competition reduced GRWR for nearly all species pairs (fig. 1B). The strongest impacts of competition were of B. diandrus and B. hordeaceus on each other, resulting in growth rates reduced by 95%–96.4% relative to the absence of competition. Elymus glaucus and S. pulchra were also subject to competition with each other, reducing S. pulchra’s growth rate 49.3%–51% and _E. glaucus_’s growth rate by 72.7%–73.6% relative to growth rates in absence of competition. The impacts of B. diandrus and B. hordeaceus on the perennials were of similar magnitude to the observed perennial-perennial impacts.
Predicted Community Composition Is Exotic Annual Dominated
We next sought to investigate competitive outcomes when all five species compete simultaneously. Although it would be possible to perform a multispecies invasion analysis, such analyses can provide misleading results because GRWR exceeding 1 does not necessarily imply stable persistence when more than two species are included (Case 1995; Dormann and Roxburgh 2005; Saavedra et al. 2017). Instead, we examined the outcomes of competition by directly assessing the final simulated community composition across a range of empirically observed densities as initial conditions. For this analysis (fig. 2A), we included the impact of foliar fungal infection on demographic rates but not the pathogen BFOD.
Figure 2:
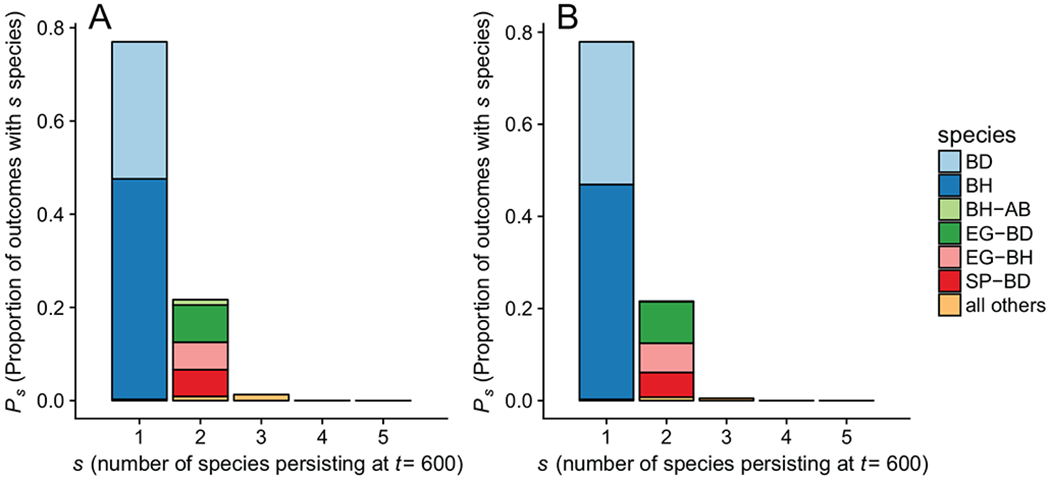
Proportion of outcomes in which a given species or species combination persisted after 600 generations in the population-dynamic model. Each replicate represents a single sample from the posterior distribution of the model parameters and initial competitor densities from a randomly sampled transect from among the set of transects that we measured. The _X_-axis corresponds to the number of species (s) that persisted over 600 simulated years, while the _Y_-axis corresponds to the proportion of replicates (Ps) that resulted in this outcome. Each bar is subdivided into the specific set of species that were observed to have log of growth rate when rare greater than 0 for a particular parameter set and transect sample. All compositions that occurred in under 1% of replicates are grouped into a single color. A, Results from a model that includes foliar fungal infection but not the black fingers of death (BFOD). B, Results from the model that includes both foliar fungal infection and BFOD. Perennial native species: Elymus glaucus (EG), Stipa pulchra (SP); annual exotic species: Bromus diandrus (BD), Bromus hordeaceus (BH), Avena barbata (AB).
Based on our two-species competition observations (fig. 1), we expected that either B. hordeaceus or B. diandrus would persist in most simulations because they have large growth rates even when invading a monoculture of native perennial competitors. Since this species pair displayed large interspecific competition coefficients, we also expected that they would rarely coexist. The pairwise invasion analysis also suggests that A. barbata should rarely persist given its low growth rate in the presence of its competitors and that the native perennials S. pulchra and E. glaucus would sometimes persist, given that their mean replacement rates were typically near one (fig. 1A). Consistent with these expectations, either B. hordeaceus or B. diandrus persisted in 99.7% of simulation replicates (fig. 2A), while the two species almost never coexisted with each other (0.32% of replicates). Avena barbata was nearly always excluded. Native perennials persisted in 22.0% of replicates, usually by coexisting with either B. hordeaceus or B. diandrus, but rarely coexisting with each other (0.39% of replicates).
The wide range of possible outcomes could reflect either uncertainty in the parameter estimates or dependence on the initial conditions of our simulations. To differentiate between these possibilities, we investigated persistence as a function of initial competitor densities (fig. 3). If each species’ success is strongly dependent on initial conditions, this suggests that priority effects play a much larger role in determining community composition than uncertainty in parameter estimates, and vice versa. We observed that the perennial species’ persistence in multispecies competition was weakly dependent on initial community composition: the probability of S. pulchra persistence increased modestly with its initial density. By contrast, the annual species B. hordeaceus and B. diandrus showed striking priority effects driven by strong interspecific competition across the densities of all competitors except A. barbata, which had only modest effects on any species.
Figure 3:
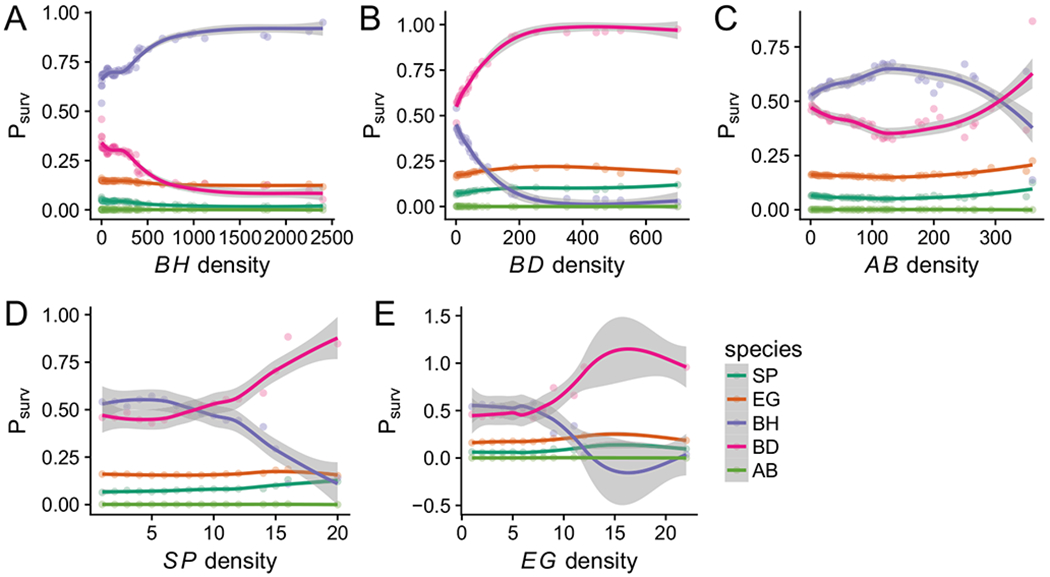
Effect of initial conditions on the outcome of competition. Estimated probability of persistence (_P_surv) of each species (colored points and lines) as a function of initial density of each species in the simulation (_X_-axis). Points represent the proportion of simulations resulting in persistence that were initialized at the corresponding density, while loess curves (and gray uncertainty envelopes) were fit with the function geom_smooth in ggplot. Perennial native species: Stipa pulchra (SP), Elymus glaucus (EG); annual exotic species: Bromus hordeaceus (BH), Bromus diandrus (BD), Avena barbata (AB). Priority effects occur when the probability of persistence depends strongly on initial density.
Nonhierarchical Competition between Natives and Exotics
Notably, the two native perennial species were not equally likely to coexist with each of the dominant exotic annuals: S. pulchra was much more likely to coexist with B. diandrus than B. hordeaceus. To better understand the dynamics driving these outcomes, we compared invasion simulations that included only the native perennials to simulations in which an exotic annual invader preceded the native perennial invader.
When the native perennials competed in the absence of exotic annuals, their dynamics are nearly neutral, as indicated by the near equality of intraspecific and interspecific competition strength (fig. 1A). Although neutral dynamics cannot result in long-term stable coexistence, they are expected to result in relatively slow loss of one of the species (Adler et al. 2007). Nearly neutral dynamics could result in priority effects if interspecific competition is slightly stronger than intraspecific competition. Consistent with these expectations, we observed slow replacement dynamics and priority effects when the native perennial species competed directly (fig. 4A). When S. pulchra was introduced first, 36.4% of simulation replicates resulted in dominance by S. pulchra, whereas 99.9% of replicates in which E. glaucus was introduced first resulted in dominance by E. glaucus. The two perennial species coexisted in only 0.1% of replicates.
We next tested how the invasion of exotic annuals might alter competition outcomes between the two perennial species. When B. diandrus invaded simulated monocultures of S. pulchra, the priority effect preventing E. glaucus from invading was substantially stronger. Among replicates in which S. pulchra and B. diandrus coexisted, E. glaucus was able to invade in only 4.5% (as compared to 52.9% of these same parameter sets when B. diandrus was not included in the simulation). Hence, when coexistence was predicted between S. pulchra and B. diandrus, the presence of the exotic annual B. diandrus increased the likelihood of persistence for S. pulchra at the expense of E. glaucus (fig. 4). These results suggest a strong impact of nonhierarchical competition on outcomes in this system, in which no single species can dominate and coexistence is only possible given specific arrival orders. These dynamics result in deterministic competitive exclusion or coexistence mediated by priority effects that make the final composition dependent on stochastic arrival order.
Seed Infection Hampers a Weak Competitor, A. barbata
While the simulation and invasion results suggest that exotic annuals will dominate perennials and either competitively exclude them or reduce their population sizes, pathogens could reduce this effect if exotic annuals incur a higher fitness cost than perennials from infection. We repeated the simulation experiments in the previous section with the impact of fungal infection by BFOD included (fig. 2B). BFOD decreased the overall success of A. barbata, which was already the weakest annual competitor. Avena barbata persisted in 1.98% of replicates that excluded BFOD but almost never persisted in its presence (0.12% of replicates). Species other than A. barbata were only minimally affected by BFOD, consistent with low rates of infection that we observed empirically (fig. A2).
Discussion
The long-term outcome of competition is difficult to observe directly in nature, so empirically parameterized mathematical models are critical for predicting when competitive exclusion, coexistence, or priority effects are most likely. To date, most studies have focused on pairwise outcomes in multispecies communities, emphasizing the relative strength of niche differences versus fitness differences (Levine and HilleRisLambers 2009; Adler et al. 2010; Narwani et al. 2013; Godoy and Levine 2014; Godoy et al. 2014; Kraft et al. 2015). By contrast, we found a large degree of niche overlap in an empirically parameterized model of an invaded California grassland fig. 1A). The model suggests that competition in multispecies assemblages can lead to complex outcomes that mix deterministic competitive exclusion or coexistence with stochastic priority effects that determine the identity of persisting species. Although a previous model predicted exotic annual dominance over native perennials, with a small probability of native coexistence with exotics, it did not predict priority effects among pairs of exotic or native species because it relied solely on a pairwise approach and composite parameter estimates from a range of species (Mordecai et al. 2015). Our work supports the results from a growing body of theoretical studies suggesting that competitive outcomes in complex communities can depart from predictions from pairwise species comparisons (Case 1995; Allesina and Levine 2011; Mayfield and Stouffer 2017; Saavedra et al. 2017) and provides evidence that slowly occurring, nearly neutral dynamics may play an important role in competitive outcomes (Adler et al. 2007). The results suggest that methods for assessing the outcome of competition in multispecies assemblages that move beyond invasion analyses are an important avenue for theoretical and empirical development (Saavedra et al. 2017; Barabás et al. 2018).
We found that the population growth model parameterized with field estimates of demographic rates accurately predicted species densities in monoculture (fig. A6), suggesting that it can realistically capture equilibrium outcomes. In this five-species assemblage, we found species pairs with high niche overlap—exotic annuals Bromus diandrus and Bromus hordeaceus; and native perennials Elymus glaucus and _Stipa pulchra_—and nonhierarchical competition such that no single species was dominant over all others (fig. 1). This results in a complex posterior distribution of competitive outcomes that includes competitive exclusion of all other species by either B. diandrus or B. hordeaceus or coexistence of one of these exotic annuals with one native perennial, either E. glaucus or S. pulchra (fig. 2). The outcome of competition between the two congeneric exotic annuals was driven by strong interspecific competition, resulting in priority effects (fig. 3). Among the subset of outcomes in which coexistence was predicted between S. pulchra and B. diandrus, the presence of B. diandrus usually prevented the subsequent invasion of E. glaucus, augmenting the priority effect exerted by S. pulchra on its native perennial competitor through nonhierarchical competition. Hence, invasion by an exotic species with moderate niche overlap may increase resilience to invasion by native competitors with high niche overlap. Since the two native species are predicted to compete nearly neutrally in the model, almost all predicted outcomes precluded their long-term stable coexistence, meaning that S. pulchra may indirectly benefit from invasion by B. diandrus via its negative effect on E. glaucus (fig. 4).
Studies applying modern coexistence theory have often documented substantial niche differences between species pairs, while variation in the magnitude of fitness difference determines the potential for coexistence or competitive exclusion. However, these studies typically explore communities in which species have long coevolutionary histories and belong to similar functional guilds (e.g., native annual forbs; Levine and HilleRisLambers 2009; Adler et al. 2010; Narwani et al. 2013; Godoy et al. 2014; Kraft et al. 2015; but see Godoy and Levine 2014). In such systems, we might expect that co-occurrence over long timescales has led species to minimize their fitness differences, maximize their niche differences, or both, leading to long-term stable coexistence. In invaded systems, exotic species must have fitness advantages, niche differences, or both with respect to the native species in order to have successfully invaded (Mac-Dougall et al. 2009). Our study found support for large fitness advantages of invading species and modest niche overlap that was potentially small enough to promote coexistence (20% posterior probability). This is consistent with the possibility that competitive exclusion and priority effects may be common long-term outcomes in invaded communities. Despite the a priori expectation of strong stabilization within co-evolved communities, our study did not identify substantial niche differences between the two native species or the two exotic Bromus species with an overlapping European home range. Instead, the results suggest that nearly neutral dynamics determine competitive outcomes in some pairs of species with long coevolutionary histories.
Among the mechanisms that may maintain diversity in complex communities, intransitive competition has received a great deal of interest (Laird and Schamp 2006; Allesina and Levine 2011; Soliveres et al. 2015; Matías et al. 2018; Stouffer et al. 2018). However, a recent study using empirically parameterized population-dynamic models found that intransitive competition was uncommon and not likely to promote coexistence among a set of 18 competing annual grass species (Godoy et al. 2017). In our study, although we found evidence for nonhierarchical competition, simulations suggested that it was unlikely to promote coexistence of more than two species. However, this does not imply that nonhierarchical competition has no role in diversity maintenance. Priority effects, like those reported here, could lead to a spatial patchwork of competitors, with disturbance and stochastic recolonization determining the distribution of competing species.
Previous empirical work on the outcome of competition in invaded California grasslands has suggested a wide range of possible outcomes and coexistence mechanisms, including (1) the requirement for previous disturbance to explain the invasion of exotics in perennial-dominated plots (Stromberg and Griffin 1996; Seabloom et al. 2003; Corbin and D’Antonio 2004), (2) competitive dominance of exotic annuals over S. pulchra (Dyer and Rice 1997), and (3) spatial variation in outcomes determined by seed dispersal (Di-Vittorio et al. 2007) and habitat (Everard et al. 2009). A limitation of most previous work considering more than two competing species is that the empirical results were not linked to a dynamic model, making it difficult to project dynamics over long timescales. Our parameterized model is inconsistent with prediction 1 because it predicts that exotic species can invade undisturbed perennial plots and consistent with prediction 2 because a portion of predicted outcomes led to unconditional exotic dominance, as predicted in a previous two-species model (Mordecai et al. 2015). Interestingly, our model projections are broadly consistent with co-occurrence observations made in the field—despite having only a few observations of each species within our transects, we found a modest anticorrelation between the two Bromus species (ρ = −0.22), as would be predicted by our model. Our qualitative field observations also suggest that these species exist predominantly in separate patches within Jasper Ridge.
While our study did not attempt to assess environmental and spatial variation in competitive outcomes (i.e., prediction 3 above), coexistence mechanisms occurring over broad temporal and spatial scales may be an important contributor to observed species distributions. The five focal species in our system have co-occurred at the study site and other California grassland sites for more than a hundred years, implying that co-occurrence may be driven by nonequilibrium dynamics that play out over long timescales or that stabilizing processes occur over larger spatial or temporal scales. Although soil moisture and nutrient availability vary spatially at both neighborhood and regional scales across California grasslands and precipitation varies several-fold between years, demographic studies of species interactions are regularly conducted at small spatial and temporal scales, as in the present study (Seabloom et al. 2003; Corbin and D’Antonio 2004; DiVittorio et al. 2007). Environmental variation combined with the long life spans of perennial bunchgrasses and the high seed production of annual grasses could provide ample opportunity for environmental fluctuations to promote coexistence over space or time (Warner and Chesson 1985; Cáceres 1997; Chesson 2000; Chesson et al. 2005; Usinowicz et al. 2017; Li and Chesson 2018). An alternative to larger-scale stabilizing processes is that priority effects occur at small spatial scales, while the turnover and random colonization of sites allows patches of different species composition to persist in a matrix of mutually noninvasible patches (Vannette and Fukami 2014). Our results are consistent with this priority effect mechanism and do not preclude the possibility of coexistence mechanisms occurring over larger scales. A major challenge for future work in systems with large and variable geographic ranges is to incorporate multiscale spatial and temporal variation that may contribute to patterns of co-occurrence.
In addition to the outcome of competition, identifying explanatory mechanisms is paramount for understanding the assembly of ecological communities and their potential to respond to species invasions. Pathogens are widely hypothesized to promote species diversity by specializing on common host species, causing a demographic disadvantage to common species and an advantage to rare species (Augspurger 1983; Augspurger and Kelly 1984; Gilbert et al. 1994; Petermann et al. 2008; Mordecai 2011, 2013; Bagchi et al. 2014). As with strong niche differences more generally, this Janzen-Connell effect has been demonstrated mostly in native-dominated plant communities (Augspurger 1983, 1984; Augspurger and Kelly 1984; Gilbert et al. 1994; Petermann et al. 2008; Bagchi et al. 2014). By contrast, pathogen impacts in this invaded grassland community differ in two important ways. First, the foliar fungal pathogens in this community typically infect multiple grass hosts, including native and exotic species (Spear and Mordecai 2018). Second, the demographic impacts were mostly minimal, except the negative impact exerted by the BFOD pathogen on A. barbata (fig. 2B). Another study in this system found no evidence that pathogen load or impacts increased on locally common species, suggesting that coexistence is not substantially affected by fungal infection (Spear and Mordecai 2018). However, because the two native perennial species compete almost neutrally in our model, even modest pathogen impacts could have a substantial effect; because their fitness differences are small, our study may have been underpowered to investigate this specific outcome.
Though the outcome of competition in invaded systems is often poorly understood, our work shows that stabilizing niche differences, and particularly the role of pathogens in that stabilization, are not ubiquitous at local scales in nature, especially in systems with short coevolutionary histories between species. Assessing the strength of stabilization and the outcome of competition is important not only for fundamental ecological understanding but also for maintaining resilient ecosystems as they respond to global change. Future work in other systems that are potentially far from equilibrium, such as invaded ecosystems, is necessary to test the generality of our results and to predict the long-term outcome of competition in nature.
Supplementary Material
Appendix

The bunchgrass Stipa pulchra, the state grass of California, is found in patches in Jasper Ridge Biological Preserve. The authors studied the ecological processes that determine the success or failure of native grasses and found that the order of arrival of invasive European grass species has a major impact on plant community composition. Photo credit: Reuben Brandt.
Acknowledgments
We thank our editors and anonymous reviewers at The American Naturalist for comments that improved the quality of the manuscript. We acknowledge generous support and assistance from Teri Barry, Nona Chiariello, Phillippe Cohen, Joe Sertich, Reuben Brandt, Johannah Farner, Steve Gomez, Bill Gomez, Stuart Koretz, Cary Tronson, Divya Ramani, Ryan Tabibi, Esther Liu, Sandya Kalavacherla, Vidya Raghvendra, Jason Zhou, Virginia Parra, Claudia Amadeo-Luyt, Gaurika Duvar, Elizabeth Wallace, the Jasper Ridge Kennedy endowment fund, the Stanford University Vice Provost for Undergraduate Education summer research fellowship for undergraduates, and the Stanford University Raising Interest in Science and Engineering (RISE) summer internship program. We thank members of the Fukami, Peay, and Mordecai labs for helpful comments on the project and Rodrigo R. Granjel, Ignasi Bartomeus, Oscar Godoy, and members of the Biotic Interactions and Global Change group for their peer review of our manuscript. L.H.U. was supported by the National Institutes of Health Institutional Research and Academic Career Development Awards fellowship (NIGMS grant K12GM088033). E.A.M. was supported by a grant from the National Science Foundation (DEB 1518681).
Footnotes
Online enhancements: appendix.
Literature Cited
- Ackerly D, Knight C, Weiss S, Barton K, and Starmer K. 2002. Leaf size, specific leaf area and microhabitat distribution of chaparral woody plants: contrasting patterns in species level and community level analyses. Oecologia 130:449–457. [DOI] [PubMed] [Google Scholar]
- Adler PB, Ellner SP, and Levine JM. 2010. Coexistence of perennial plants: an embarrassment of niches. Ecology Letters 13:1019–1029. [DOI] [PubMed] [Google Scholar]
- Adler PB, HilleRisLambers J, Kyriakidis PC, Guan Q, and Levine JM. 2006. Climate variability has a stabilizing effect on the coexistence of prairie grasses. Proceedings of the National Academy of Sciences of the USA 103:12793–12798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adler PB, HilleRisLambers J, and Levine JM. 2007. A niche for neutrality. Ecology Letters 10:95–104. [DOI] [PubMed] [Google Scholar]
- Allesina S, and Levine JM. 2011. A competitive network theory of species diversity. Proceedings of the National Academy of Sciences of the USA 108:5638–5642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Augspurger CK 1983. Seed dispersal of the tropical tree, Platypodium elegans, and the escape of its seedlings from fungal pathogens. Journal of Ecology 71:759–771. [Google Scholar]
- —. 1984. Seedling survival of tropical tree species: interactions of dispersal distance, light-gaps, and pathogens. Ecology 65:1705–1712. [Google Scholar]
- Augspurger CK, and Kelly CK. 1984. Pathogen mortality of tropical tree seedlings: experimental studies of the effects of dispersal distance, seedling density, and light conditions. Oecologia 61:211–217. [DOI] [PubMed] [Google Scholar]
- Bagchi R, Gallery RE, Gripenberg S, Gurr SJ, Narayan L, Addis CE, Freckleton RP, and Lewis OT. 2014. Pathogens and insect herbivores drive rainforest plant diversity and composition. Nature 506:85–88. [DOI] [PubMed] [Google Scholar]
- Barabás G, D’Andrea R, and Stump SM. 2018. Chesson’s coexistence theory. Ecological Monographs 88:277–303. [Google Scholar]
- Beckstead J, Meyer SE, Connolly BM, Huck MB, and Street LE. 2010. Cheatgrass facilitates spillover of a seed bank pathogen onto native grass species. Journal of Ecology 98:168–177. [Google Scholar]
- Burdon J, and Chilvers G. 1974. Fungal and insect parasites contributing to niche differentiation in mixed species stands of eucalypt saplings. Australian Journal of Botany 22:103–114. [Google Scholar]
- Cáceres CE 1997. Temporal variation, dormancy, and coexistence: a field test of the storage effect. Proceedings of the National Academy of Sciences of the USA 94:9171–9175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter SR, Cole JJ, Pace ML, Batt R, Brock W, Cline T, Coloso J, et al. 2011. Early warnings of regime shifts: a whole-ecosystem experiment. Science 332:1079–1082. [DOI] [PubMed] [Google Scholar]
- Case TJ 1995. Surprising behavior from a familiar model and implications for competition theory. American Naturalist 146:961–966. [Google Scholar]
- Chesson P 2000. Mechanisms of maintenance of species diversity. Annual Review of Ecology and Systematics 31:343–366. [Google Scholar]
- Chesson P, Donahue MJ, Melbourne BA, and Sears AL. 2005. Scale transition theory for understanding mechanisms in metacommunities. Pages 279–306_in_Holyoak M, Leibold MA, and Holt RD, eds. Metacommunities: spatial dynamics and ecological communities. University of Chicago Press, Chicago. [Google Scholar]
- Corbin JD, and D’Antonio CM. 2004. Competition between native perennial and exotic annual grasses: implications for an historical invasion. Ecology 85:1273–1283. [Google Scholar]
- DiVittorio CT, Corbin JD, and D’Antonio CM. 2007. Spatial and temporal patterns of seed dispersal: an important determinant of grassland invasion. Ecological Applications 17:311–316. [DOI] [PubMed] [Google Scholar]
- Dormann CF, and Roxburgh SH. 2005. Experimental evidence rejects pairwise modelling approach to coexistence in plant communities. Proceedings of the Royal Society B 272:1279–1285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dyer A, and Rice K. 1997. Intraspecific and diffuse competition: the response of Nassella pulchra in a California grassland. Ecological Applications 7:484–492. [Google Scholar]
- Everard K, Seabloom EW, Harpole WS, and de Mazancourt C. 2009. Plant water use affects competition for nitrogen: why drought favors invasive species in California. American Naturalist 175:85–97. [DOI] [PubMed] [Google Scholar]
- Fukami T, Bezemer TM, Mortimer SR, and van der Putten WH. 2005. Species divergence and trait convergence in experimental plant community assembly. Ecology Letters 8:1283–1290. [Google Scholar]
- Fukami T, Mordecai EA, and Ostling A. 2016. A framework for priority effects. Journal of Vegetation Science 27:655–657. [Google Scholar]
- Gilbert G, Foster R, and Hubbell S. 1994. Density and distance-to-adult effects of a canker disease of trees in a moist tropical forest. Oecologia 98:100–108. [DOI] [PubMed] [Google Scholar]
- Godoy O, Kraft NJ, and Levine JM. 2014. Phylogenetic relatedness and the determinants of competitive outcomes. Ecology Letters 17:836–844. [DOI] [PubMed] [Google Scholar]
- Godoy O, and Levine JM. 2014. Phenology effects on invasion success: insights from coupling field experiments to coexistence theory. Ecology 95:726–736. [DOI] [PubMed] [Google Scholar]
- Godoy O, Stouffer DB, Kraft NJ, and Levine JM. 2017. Intransitivity is infrequent and fails to promote annual plant coexistence without pairwise niche differences. Ecology 98:1193–1200. [DOI] [PubMed] [Google Scholar]
- HilleRisLambers J, Adler P, Harpole W, Levine J, and Mayfield M. 2012. Rethinking community assembly through the lens of coexistence theory. Annual Review of Ecology, Evolution, and Systematics 43:227–248. [Google Scholar]
- Holt RD, Grover J, and Tilman D. 1994. Simple rules for interspecific dominance in systems with exploitative and apparent competition. American Naturalist 144:741–771. [Google Scholar]
- Kraft NJ, Godoy O, and Levine JM. 2015. Plant functional traits and the multidimensional nature of species coexistence. Proceedings of the National Academy of Sciences of the USA 112:797–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird RA, and Schamp BS. 2006. Competitive intransitivity promotes species coexistence. American Naturalist 168:182–193. [DOI] [PubMed] [Google Scholar]
- Levine JM, and HilleRisLambers J. 2009. The importance of niches for the maintenance of species diversity. Nature 461:254–257. [DOI] [PubMed] [Google Scholar]
- Li YM, and Chesson P. 2018. Seed demographic comparisons reveal spatial and temporal niche differentiation between native and invasive species in a community of desert winter annual plants. Evolutionary Ecology Research 19:71–84. [Google Scholar]
- MacDougall AS, Gilbert B, and Levine JM. 2009. Plant invasions and the niche. Journal of Ecology 97:609–615. [Google Scholar]
- Mack RN 1989. Temperate grasslands vulnerable to plant invasions: characteristics and consequences. Pages 155–179_in_Drake J, Mooney H, and Di Castri F, eds. Biological invasions: a global perspective. Wiley, New York. [Google Scholar]
- Matías L, Godoy O, Gómez-Aparicio L, and Pérez-Ramos IM. 2018. An experimental extreme drought reduces the likelihood of species to coexist despite increasing intransitivity in competitive networks. Journal of Ecology 106:826–837. [Google Scholar]
- Mayfield MM, and Stouffer DB. 2017. Higher-order interactions capture unexplained complexity in diverse communities. Nature Ecology and Evolution 1:0062. [DOI] [PubMed] [Google Scholar]
- Mordecai EA 2011. Pathogen impacts on plant communities: unifying theory, concepts, and empirical work. Ecological Monographs 81:429–441. [Google Scholar]
- —. 2012. Soil moisture and fungi affect seed survival in California grassland annual plants. PLoS ONE 7:e39083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- —. 2013. Despite spillover, a shared pathogen promotes native plant persistence in a cheatgrass-invaded grassland. Ecology 94:2744–2753. [DOI] [PubMed] [Google Scholar]
- Mordecai EA, Molinari NA, Stahlheber KA, Gross K, and D’Antonio C. 2015. Controls over native perennial grass exclusion and persistence in California grasslands invaded by annuals. Ecology 96:2643–2652. [DOI] [PubMed] [Google Scholar]
- Myers N, Mittermeier RA, Mittermeier CG, Da Fonseca GA, and Kent J. 2000. Biodiversity hotspots for conservation priorities. Nature 403:853–858. [DOI] [PubMed] [Google Scholar]
- Narwani A, Alexandrou MA, Oakley TH, Carroll IT, and Cardinale BJ. 2013. Experimental evidence that evolutionary relatedness does not affect the ecological mechanisms of coexistence in freshwater green algae. Ecology Letters 16:1373–1381. [DOI] [PubMed] [Google Scholar]
- Ocampo-Ariza C, Bufford JL, Hulme PE, Champion PD, and Godsoe W. 2018. Strong fitness differences impede coexistence between an alien water fern (Azolla pinnata r. br.) and its native congener (Azolla rubra r. br.) in New Zealand. Biological Invasions 20:1–9. [Google Scholar]
- Petermann JS, Fergus AJ, Turnbull LA, and Schmid B. 2008. Janzen-Connell effects are widespread and strong enough to maintain diversity in grasslands. Ecology 89:2399–2406. [DOI] [PubMed] [Google Scholar]
- Saavedra S, Rohr RP, Bascompte J, Godoy O, Kraft NJ, and Levine JM. 2017. A structural approach for understanding multispecies coexistence. Ecological Monographs 87:470–486. [Google Scholar]
- Seabloom EW, Harpole WS, Reichman O, and Tilman D. 2003. Invasion, competitive dominance, and resource use by exotic and native California grassland species. Proceedings of the National Academy of Sciences of the USA 100:13384–13389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soliveres S, Maestre FT, Ulrich W, Manning P, Boch S, Bowker MA, Prati D, et al. 2015. Intransitive competition is widespread in plant communities and maintains their species richness. Ecology Letters 18:790–798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spear ER, and Mordecai EA. 2018. Foliar pathogens of California grasses are multi-host and spatially widespread: implications for grassland diversity. Ecology 99:2250–2259. [DOI] [PubMed] [Google Scholar]
- Staver AC, Archibald S, and Levin SA. 2011. The global extent and determinants of savanna and forest as alternative biome states. Science 334:230–232. [DOI] [PubMed] [Google Scholar]
- Stouffer DB, Wainwright CE, Flanagan T, and Mayfield MM. 2018. Cyclic population dynamics and density-dependent intransitivity as pathways to coexistence between co-occurring annual plants. Journal of Ecology 106:838–851. [Google Scholar]
- Stromberg MR, and Griffin JR. 1996. Long-term patterns in coastal California grasslands in relation to cultivation, gophers, and grazing. Ecological Applications 6:1189–1211. [Google Scholar]
- Tilman D 1980. Resources: a graphical-mechanistic approach to competition and predation. American Naturalist 116:362–393. [Google Scholar]
- Turelli M 1978. Does environmental variability limit niche overlap? Proceedings of the National Academy of Science of the USA 75: 5085–5089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turnbull LA, Manley L, and Rees M. 2005. Niches, rather than neutrality, structure a grassland pioneer guild. Proceedings of the Royal Society B 272:1357–1364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Usinowicz J, Chang-Yang C-H, Chen Y-Y, Clark JS, Fletcher C, Garwood NC, Hao Z, et al. 2017. Temporal coexistence mechanisms contribute to the latitudinal gradient in forest diversity. Nature 550:105–108. [DOI] [PubMed] [Google Scholar]
- Vannette RL, and Fukami T. 2014. Historical contingency in species interactions: towards niche-based predictions. Ecology Letters 17:115–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warner RR, and Chesson PL. 1985. Coexistence mediated by recruitment fluctuations: a field guide to the storage effect. American Naturalist 125:769–787. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix