Bayesian Association-Based Fine Mapping in Small Chromosomal Segments (original) (raw)
Abstract
A Bayesian method for fine mapping is presented, which deals with multiallelic markers (with two or more alleles), unknown phase, missing data, multiple causal variants, and both continuous and binary phenotypes. We consider small chromosomal segments spanned by a dense set of closely linked markers and putative genes only at marker points. In the phenotypic model, locus-specific indicator variables are used to control inclusion in or exclusion from marker contributions. To account for covariance between consecutive loci and to control fluctuations in association signals along a candidate region we introduce a joint prior for the indicators that depends on genetic or physical map distances. The potential of the method, including posterior estimation of trait-associated loci, their effects, linkage disequilibrium pattern due to close linkage of loci, and the age of a causal variant (time to most recent common ancestor), is illustrated with the well-known cystic fibrosis and Friedreich ataxia data sets by assuming that haplotypes were not available. In addition, simulation analysis with large genetic distances is shown. Estimation of model parameters is based on Markov chain Monte Carlo (MCMC) sampling and is implemented using WinBUGS. The model specification code is freely available for research purposes from http://www.rni.helsinki.fi/~mjs/.
METHODS for association-based gene mapping use genetic markers that lie near the causative genes as gene representatives in their phenotypic models. How successful these methods are, or how much the original gene effect is reduced when measured indirectly through the closest marker, depends on existing covariance (linkage disequilibrium, LD) between the marker and the gene (Tanksley 1993). The magnitude of LD again depends on factors like population history and the distance between the two loci. In association analysis we are especially interested in using LD due to close linkage of loci as a detection signal, which depends according to exponential decay on the distance between the two loci and would give its highest value at a gene position. Thus, we want to exclude confounding effects (e.g., mutation, selection, genetic drift, population structure, and variations in allele frequencies) from the association signal (measured LD).
Association analysis has been recognized as an important and complementary tool for mapping genes in human, animals, and plants (Risch and Merikangas 1996; Flint and Mott 2001). Effective methods are currently available for finding trait-associated subsets of candidate markers using collected samples of equally related or unrelated individuals (Ball 2001; Piepho and Gauch 2001; Sen and Churchill 2001; Broman and Speed 2002; Devlin et al. 2003; Kilpikari and Sillanpää 2003; Xu 2003; Yi et al. 2003). These methods use modern procedures for candidate selection but they do not account for covariance between closely linked markers or control fluctuations in association signals. Accounting for such factors may improve gene localization in fine-mapping studies, where a large number of markers have been collected from small chromosomal regions.
Conti and Witte (2003) considered the covariance between the loci in their semi-Bayesian approach. Instead of trying to find some initial evidence for the gene, they wanted to increase the ability to localize disease genes in situations where support for some particular genome region has already been established by statistical or biological means. In their method, the genetic effect coefficient, which is a pairwise measure of LD, is first estimated for each locus using a first-stage model and then spatially smoothed along the candidate region using a second-stage model that can include information on genetic or physical distances (and/or haplotype blocks). This smoothing approach does not require knowledge about haplotypes (linkage phases) and it can control fluctuations in pairwise measures of LD (effect estimate) that may arise from reasons other than tight linkage of loci. Such reasons include population history, structure, and events, as well as allele frequency differences between loci and small sample size (Clayton 2000; Greenland et al. 2000; Nordborg and Tavare 2002; Conti and Witte 2003). Unfortunately their approach is feasible only for biallelic markers (where it is easy to infer coupling of alleles between loci) and one cannot consider more than a single locus at a time in the first-stage model (because other loci would confound the pairwise signal). For other approaches that consider covariance between neighboring loci, see Lazzeroni (1998) and Cordell and Elston (1999).
Utilization of marker distances is common in fine-mapping methods, which either assume known linkage phases or technically sum (integrate) over all possible haplotype configurations that are consistent with the genotype data (Rannala and Slatkin 1998; McPeek and Strahs 1999; Service et al. 1999; Morris et al. 2000, 2003a,b; Thomas et al. 2003; Durrant et al. 2004). These methods account for covariance between haplotypes (LD due to common population history) and often consider putative gene positions that can be different from the marker positions. Instead of trying to consider more than a single gene locus at a time in their disease model, these approaches concentrate on reconstructing ancestral disease haplotypes or modeling related recombination histories. The fine-scale LD mapping methods generally assume a discrete phenotype (unlike Meuwissen and Goddard 2000) and ignore the population stratification (Lazzeroni 2001).
We consider only marker positions as putative gene loci in our association-based method. Our approach is based on Bayesian analysis with multiple-trait loci, where locus-specific indicator variables are used to control inclusion or exclusion of a particular set of allelic coefficients in the multiple-regression model. In general, several approaches utilize locus-specific indicator variables for model selection (Uimari and Hoeschele 1997; Conti et al. 2003; Yi et al. 2003; Meuwissen and Goddard 2004; Yi 2004). Instead of following others and requiring that the indicators are mutually independent a priori, we allow their prior dependence structure to exploit the distance information. This kind of prior is motivated by its ability to control fluctuations in association signals (LD measured from locus indicators) along a candidate region (see Figure 1). [Note that this treatment makes our approach directly applicable for genotype data from multiallelic (polymorphic) markers, unlike that of Conti and Witte (2003), who modeled marker dependency in effect estimates.] To control the number of selected markers, we let the values of the indicators have a tendency to shrink toward zero; this idea is modified from the approaches of Meuwissen et al. (2001) and Xu (2003). The presented model was implemented using the Markov chain Monte Carlo software package WinBUGS (Gilks et al. 1994; Spiegelhalter et al. 1999). To illustrate the performance of our approach we analyze the well-known cystic fibrosis data set of Kerem et al. (1989), utilizing available physical distances but assuming only genotype data. Additionally we analyze Friedreich ataxia data of Liu et al. (2001) and simulated data of Kilpikari and Sillanpää (2003) with genetic distances and assuming no haplotype information.
Figure 1.—
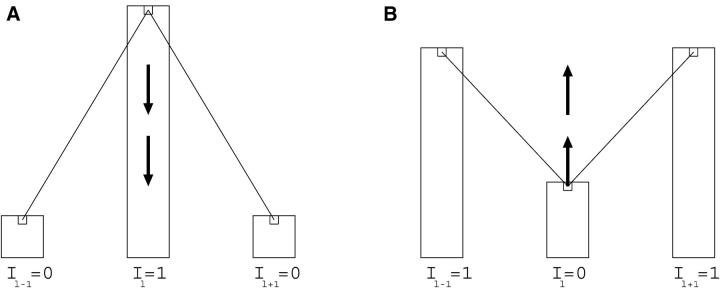
Illustration of how dependence between adjacent markers influences the mapping signal (QTL probability on the _y_-axis). The posterior QTL probabilities are drawn as a histogram and the corresponding hypothetical values of locus indicators {_Il_−1, Il, Il+1} for three markers {l − 1, l, l + 1} are given in a single MCMC iteration. (A) Surrounding indicators smooth the spurious signal at marker l downward. (B) Surrounding indicators strengthen the weak but real signal at marker l upward. A similar phenomenon happens in methods that utilize combined information of linkage and association. In these methods, linkage information does not confirm spurious associations but strengthens the real association signals.
MODEL
Notation:
Let us consider a trait, either continuous or binary, and a small candidate region R, which consist of a discrete set of M marker loci where the putative genes (trait loci) can be positioned. We use a generic term QTL for a trait locus, with influence on a quantitative or qualitative trait, and for the closest candidate marker that is in strong LD with a trait locus. Let us denote a vector of phenotypes by y = (_y_1, _y_2, … , y _N_ind) and a vector of marker observations by 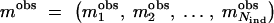 consisting of measurements from _N_ind different individuals and M marker loci. In the case of no missing data, a vector of observations _m_obs equals a complete genotype vector m = (mi), where an element mi = (_mi_1,_mi_2, … , miM) belongs to individual i. Here, each allele in pair
consisting of measurements from _N_ind different individuals and M marker loci. In the case of no missing data, a vector of observations _m_obs equals a complete genotype vector m = (mi), where an element mi = (_mi_1,_mi_2, … , miM) belongs to individual i. Here, each allele in pair 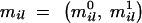 can take an integer value in range [1, _Nl_], where Nl is a number of alleles at locus l.
can take an integer value in range [1, _Nl_], where Nl is a number of alleles at locus l.
Model for missing genotype data:
We assume that there might be some missingness in the marker genotypes, _m_obs, and that their values are missing at random. To hierarchically model genotype observations (under Hardy-Weinberg equilibrium), we assume a vector of underlying population allele frequencies f = (fl), where fl consist of allele frequencies at locus l. The joint distribution of complete and incomplete (observed) marker genotypes and population allele frequencies p(_m_obs, m, f) can be factored and presented in the form p(_m_obs, m, f) = p(_m_obs|m)p(m|f)p(f). In principle, we can have an indicator function p(_m_obs|m) that takes value one or zero depending on whether the complete marker genotypes (m) are consistent or not, with the observed (incomplete) marker genotype data (_m_obs). However, in practice, WinBUGS does not need this kind of prior to generate imputed values, because missing value imputations are done conditionally on observations (see Congdon 2001). The prior for the complete genotype data
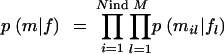
is multinomial, where the occurrence probability of each allele is obtained from the corresponding frequency in fl. We consider two alternative schemes: (1) to assume the prior for each population allele frequency fl, in 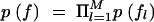 , as Dirichlet (Nl), or (2) to fix the population allele frequencies (f) to a uniform distribution over alleles at each locus; this implies p(f) = 1.
, as Dirichlet (Nl), or (2) to fix the population allele frequencies (f) to a uniform distribution over alleles at each locus; this implies p(f) = 1.
Phenotype model:
Each marker position l has its own locus-indicator variable Il, where the value one (Il = 1) corresponds to the case where the marker is included in the model as a QTL representative and value zero (Il = 0) implies exclusion. Each marker position l has its own vector of genetic effect coefficients β_l_ = (β_la_), where βla is the coefficient for allele a at marker l, where a = 1, … , Nl and l = 1, … , M. Given the vector of locus indicators I = (Il), overall mean α, and effects β = (β_l_), our genetic model with additive allelic effects for observation yi (individual i) can be written as
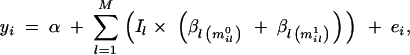 |
1 |
|---|
where residuals ei are assumed to be normally distributed N(0, 1/τ), with precision parameter 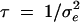 (i.e., inverse of residual variance). In the case of binary phenotypes we omit the residuals from the model (1) and consider phenotypes through a logit link function (see Uimari and Sillanpää 2001; Conti and Witte 2003; and discussion). Let
(i.e., inverse of residual variance). In the case of binary phenotypes we omit the residuals from the model (1) and consider phenotypes through a logit link function (see Uimari and Sillanpää 2001; Conti and Witte 2003; and discussion). Let 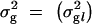 be a vector of genetic variances where an element σ2g_l_ is the genetic variance at locus l. We assume that effect coefficients β_la_ are normally distributed with N_0, σ2g_l, where in the case of biallelic markers one can use a fixed variance model and prespecify σ2g_l_ and in the case of multiallelic markers use a random variance model with unknown σ2g_l_. (In classical statistics, these two alternatives are called the fixed-effect model and the variance component model.) We allow the first coefficient (β_l_1) at each locus l to be unconstrained in our model unlike that in Kilpikari and Sillanpää (2003). Note that we can still identify differences (contrasts) from the Markov chain Monte Carlo (MCMC) sample or from MCMC point estimates of coefficients afterward.
be a vector of genetic variances where an element σ2g_l_ is the genetic variance at locus l. We assume that effect coefficients β_la_ are normally distributed with N_0, σ2g_l, where in the case of biallelic markers one can use a fixed variance model and prespecify σ2g_l_ and in the case of multiallelic markers use a random variance model with unknown σ2g_l_. (In classical statistics, these two alternatives are called the fixed-effect model and the variance component model.) We allow the first coefficient (β_l_1) at each locus l to be unconstrained in our model unlike that in Kilpikari and Sillanpää (2003). Note that we can still identify differences (contrasts) from the Markov chain Monte Carlo (MCMC) sample or from MCMC point estimates of coefficients afterward.
For loci with only a few segregating alleles or haplotypes, one can replace allele-specific effects in model (1) with genotype-specific (dominance) or haplotype-specific coefficients (Kilpikari and Sillanpää 2003) using a fixed-variance model. To use genotype- or haplotype-specific coefficients in the presence of a larger number of alleles/haplotypes, one should use a random-variance model. See the discussion for alternate ways of handling a large number of coefficients.
Hierarchical model:
One needs to prespecify the following in the model: (1) the prior expectation of the proportion of trait-associated markers in region R, denoted as s, and (2) either the physical or genetic map distances in a vector d = (_d_2, … , dM), where an element dl refers to the distance between markers l and l − 1. Optionally, one may also prespecify an overall smoothing parameter λ in the model (see below).
From Bayes formula we obtain that the posterior density of parameters {I, α, β, σ2g, τ, λ, m, f} given the observed data (y, _m_obs) and fixed quantities {s, d}, denoted as p(I, α, β, σ2g, τ, λ, m, f|y, _m_obs, s, d), is proportional to the joint density p(y, _m_obs, I, α, β, σ2g, τ, λ, m, f|s, d). By making suitable conditional independence assumptions among variables (like assuming a priori independence between the vector of locus indicators and genetic effects; Kuo and Mallick 1998), the joint density can be presented as a product of a likelihood and a factorized prior density:
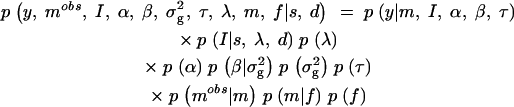
Here the p(y|m, I, α, β, τ) is a likelihood function that is obtained from the genetic model by substituting residuals ei = (yi − δ_i_) to the normal density function (see Sillanpää and Arjas 1998; Kilpikari and Sillanpää 2003); 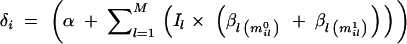 In the case of binary data and logit-link function, the likelihood takes the form
In the case of binary data and logit-link function, the likelihood takes the form 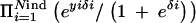 .
.
A vector containing intermarker distances d = (_d_2, … , dM) is incorporated in the prior for indicator variables
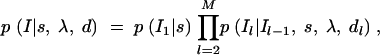
where p(_I_1|s) is a Bernoulli distribution with parameter s, where 1 − s can be interpreted as a given shrinkage factor (how much value zero is preferred over one). In our analyses, we have used s = 1/M, which corresponds to a prior belief of one QTL in region R. For some other ways of setting a prior for the number of QTL in locus-indicator models, see Yi (2004). Transition probabilities p(Il|_Il_−1, s, λ, dl) from position l − 1 to l can be arranged into the 2 × 2 matrix containing all possible transitions between states 0 and 1:
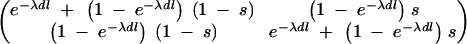 |
2 |
|---|
To understand this structure better, we can express the value of Il as a function of _Il_−1 as follows: 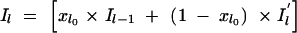 , for l = 2, … , M. Here, _xl_0 is a Bernoulli e −λdl variable with _xl_0 = 1 indicating that Il takes the same value as _Il_−1 and with xl_0 = 0 indicating that the value of Il is drawn independently of the value of the previous locus (i.e.,
, for l = 2, … , M. Here, _xl_0 is a Bernoulli e −λdl variable with _xl_0 = 1 indicating that Il takes the same value as _Il_−1 and with xl_0 = 0 indicating that the value of Il is drawn independently of the value of the previous locus (i.e., 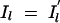 ). The probability of xl_0 being 1 depends on the distance dl between markers l and l − 1 and reflects the linkage disequilibrium in the area. Here this probability is modeled as
). The probability of xl_0 being 1 depends on the distance dl between markers l and l − 1 and reflects the linkage disequilibrium in the area. Here this probability is modeled as 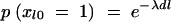 , where λ can be interpreted as an overall smoothing parameter and dl is the physical or genetic distance, expressed in kilobases or morgans, between markers l and l − 1. This will result in lower dependencies between consecutive markers if the distance between them is large and vice versa. (Note that although the apparent dependence in transition probability is one-sided, it will actually induce two-sided dependence between indicators in practice.) The new indicator I_′_l has Bernoulli distribution with shrinkage parameter s. Note that the lower diagonal term in Equation 2, p(Il = 1|Il_−1 = 1, s, λ, dl), is loosely related to the Malecot equation for isolation by distance (cf. Morton et al. 2001), where there is positive probability (depending on population size) to find association due to chance. Following Conti and Witte (2003) one may prespecify and use a fixed smoothing parameter value or perhaps use a range of different values in different MCMC chains for tuning (to introduce a preferred level of smoothing). Alternatively, we can specify a wide or a narrow prior for smoothing parameter λ. In the following we have used a Gamma(1, 0.01) prior, if not stated otherwise, with prior mean at 100. Priors for the genetic coefficients p_β_la|σ2g_l in the case of a fixed variance model (at each locus l) were assumed to be a priori independent standard normal N(0, 1), omitting a prior for genetic variance p_σ2g_l, and in the case of a random variance model p_β_la|σ2g_l is N(0, σ2g_l) with p_σ2g_l as an inverse Gamma(1, 1). Consequently we assumed
, where λ can be interpreted as an overall smoothing parameter and dl is the physical or genetic distance, expressed in kilobases or morgans, between markers l and l − 1. This will result in lower dependencies between consecutive markers if the distance between them is large and vice versa. (Note that although the apparent dependence in transition probability is one-sided, it will actually induce two-sided dependence between indicators in practice.) The new indicator I_′_l has Bernoulli distribution with shrinkage parameter s. Note that the lower diagonal term in Equation 2, p(Il = 1|Il_−1 = 1, s, λ, dl), is loosely related to the Malecot equation for isolation by distance (cf. Morton et al. 2001), where there is positive probability (depending on population size) to find association due to chance. Following Conti and Witte (2003) one may prespecify and use a fixed smoothing parameter value or perhaps use a range of different values in different MCMC chains for tuning (to introduce a preferred level of smoothing). Alternatively, we can specify a wide or a narrow prior for smoothing parameter λ. In the following we have used a Gamma(1, 0.01) prior, if not stated otherwise, with prior mean at 100. Priors for the genetic coefficients p_β_la|σ2g_l in the case of a fixed variance model (at each locus l) were assumed to be a priori independent standard normal N(0, 1), omitting a prior for genetic variance p_σ2g_l, and in the case of a random variance model p_β_la|σ2g_l is N(0, σ2g_l) with p_σ2g_l as an inverse Gamma(1, 1). Consequently we assumed 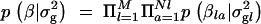 and
and 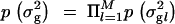 . The prior for the overall mean is N(0, 0.1) and that for the precision parameter p(τ) is Gamma(1, 1), where the latter is needed only for continuous phenotypes. Note that ideally the genetic prior variance given in a fixed variance model should be proportional to the phenotypic variance of the trait, which also can be used inversely as a natural lower bound for p(τ).
. The prior for the overall mean is N(0, 0.1) and that for the precision parameter p(τ) is Gamma(1, 1), where the latter is needed only for continuous phenotypes. Note that ideally the genetic prior variance given in a fixed variance model should be proportional to the phenotypic variance of the trait, which also can be used inversely as a natural lower bound for p(τ).
MATERIALS
To test the performance of our methodology for a binary trait with bi-allelic markers and physical distances, we selected a well-known cystic fibrosis (CF) data set that has some degree of missing alleles (Kerem et al. 1989). Additionally, we analyzed public data for Friedreich ataxia (FA), which has a binary trait with multiallelic markers and genetic distances as well as some missing data (Liu et al. 2001; Molitor et al. 2003a,b). We have illustrated the influence of choice of different types of priors (wide and narrow) and fixed values (small and large) for smoothing parameter λ and also compared the results to the case of no smoothing, with the FA data. We also wanted to compare the two previously mentioned schemes for handling of missing values between CF and FA analyses. Finally, to test performance of our methodology for a quantitative trait with multiallelic markers and large genetic distances without missing data, we analyzed the simulated data set presented in Kilpikari and Sillanpää (2003).
CF data and model:
The CF data contain 93 individuals with binary disease status and 23 biallelic markers with haplotype information. These restriction fragment length polymorphism (RFLP) markers span the area surrounding the cystic fibrosis transmembrane regulator (CFTR) gene on chromosomal segment 7q31. The physical distances in this 1.7-Mb region are available in the data (Kerem et al. 1989; Morris et al. 2000). Because it was unknown which two haplotypes belong to the same individual (within both phenotypic classes), we used a fixed-variance model with a slight modification, where only a single allelic coefficient was fitted in each selected locus; each individual contributed two independent observations (phenotype and one allele at each locus) to the analysis (cf. Sasieni 1997). It is evident that this modified model gives the same result as the model where two allelic coefficients are fitted in each selected locus, except that the estimated allelic effects (and their contrasts) are approximately double in size. It is important to note that the analysis was done by assuming that we did not have haplotypes available. Here we assumed the model for missing values, where the frequency (hyper)parameters have Dirichlet prior distributions and are estimated from the data.
FA data and model:
The Friedreich ataxia data were first published in Liu et al. (2001) and they consist of 58 disease haplotypes and 69 control haplotypes with 12 microsatellite markers covering a 15-cM region (9 closely spaced markers within a 1-cM area and 3 markers at the two ends covering the rest of the length). An extra unphased individual was omitted from the analysis. Genetic distances are available in the data. We used a random-variance model with the same modification as in CF data analysis, where each individual contributed two independent observations to the analysis. Again, haplotype information was omitted in the analysis. In the analysis we assumed a model for missing values, where each allele was considered to be a priori equally probable at each marker locus. In the analysis with no smoothing, we assumed an independent prior for locus indicators, where each indicator depends only on shrinkage parameter.
Simulated data and model:
The simulated data consist of quantitative phenotype and genotype measurements at 36 multiallelic markers (without haplotype information) from 1000 individuals; see Kilpikari and Sillanpää (2003) for details. Simulated QTL are at markers 18 (a strong effect) and 22 (a weak effect) with a joint heritability of 0.63. Haldane's function was used to convert recombination fractions to morgans. The intermarker genetic distances are wide in this data set, typically corresponding to recombination fractions of 0.1 or 0.2. The complete data set was used here (without any missing values), whereas Kilpikari and Sillanpää (2003) used the data set where 20% of the marker genotypes were missing. Unlike in CF and FA analyses, every individual contributed a single observation (one phenotype and two alleles at each locus) to the analysis where a random-variance model, with for each allele its own coefficient, was assumed.
Analyses:
Data sets were analyzed in WinBUGS 1.3 (Gilks et al. 1994; Spiegelhalter et al. 1999), using a Pentium 4, 2.8 GHz. In CF and FA analyses, where we assumed a prior distribution for λ or prior independence of locus indicators, we ran two MCMC chains each of length 30,000 (13,500 in FA analyses with fixed λ and 5500 in simulation analyses) with different initial values. First, 5000 (1000 and 4000) rounds were discarded from each chain as “burn-in,” which resulted in 50,000 (25,000 and 3000) pooled MCMC samples in total, respectively. We did not apply any “thinning” for the chain, because of sufficient computer storage capacity and low autocorrelation in the samples. The two MCMC chains were run in parallel, which took ∼20 hr with CF data and 8 (4) hr with FA data (with fixed λ) and 98 hr with simulated data. The convergence assessments were performed by visually monitoring chains for several different parameters.
RESULTS
CF data:
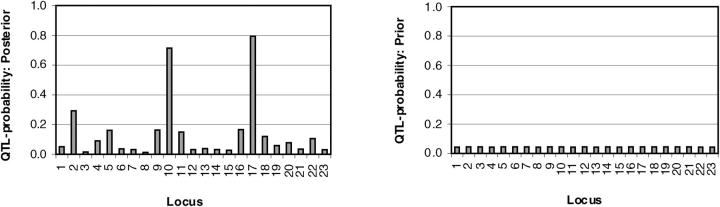
In Figure 2, we present the estimated posterior probabilities for different markers to be associated on the CF phenotype (left) and the same based on prior only (right). The posterior estimate for the number of trait loci in the whole region turned out to be ∼3 (with mean 3.24 and mode 3) where the prior assumption for the same was 1.
Figure 2.—
QTL probabilities. Locus-specific estimates of QTL probabilities for the CF data set (left) and the corresponding prior probabilities (right) are shown. Marker numbers are shown on the _x_-axis and QTL probabilities on the _y_-axis.
QTL probabilities in our model may be confounded with QTL effects. This is because in the case of strong LD (dependence), the prior of locus indicators supports several indicators to have value one simultaneously. At the same time, if the position with indicator value one is not a good explanatory variable for phenotype, the corresponding QTL effect becomes negligible. In such case, a locus-indicator value is not sufficient alone to determine how well the putative position explains the phenotype. However, we can still inspect their values as preliminary indicators of QTL activity. In particular due to the relatively small amount of LD in the data set (see below) and the “shrinkage” assumption in our model, we obtained a clear indication of QTL positions at the probability scale. Figure 2 (left) shows a distinct signal at the correct Δ_F_508 position on marker 17, which is known to account for ∼66% of the disease chromosomes (Bertranpetit and Calafell 1996). Additionally a clear signal appears at marker 10 (EG1.4) outside the CFTR region. This location as well as many others was found to have a strong secondary association in the study of Kerem et al. (1989). Moreover, Molitor et al. (2003b) used a single-locus model and found a bimodal posterior distribution for gene location with both modes within 0.03 cM of our best candidates. They also made an additional analysis where the left mode disappears in an analysis for which the only case haplotypes were those known to contain the Δ_F_508 mutation. Our method clearly identifies marker 10 as a secondary contributor in this data set. Because of this, we performed a closer inspection of haplotypes in the original data set. In Table 1, one can see that occurrences of certain alleles at markers 10 and 17 correlate with each other in haplotypes (correlation is 0.51). Moreover, one can say that correlation between markers 10 and 17 is surprisingly low (−0.02) among control individuals (Table 1, PC0), suggesting that locus 10 may have protective influence (negative susceptibility) on the disease. A possible reason why this locus has not been suggested by others is that most LD mapping approaches focus on searching for susceptibility alleles only. Note that although the posterior estimated number of trait loci was three, Figure 2 clearly supported only two locations with several neighboring locations with much smaller QTL probabilities. We believe that this estimated number reflects a marker dependency (LD) pattern rather than the actual QTL number for the region (see discussion).
TABLE 1.
CF data
| Marker | Distance | Missing | Cor | PC0 | PC1 |
|---|---|---|---|---|---|
| 1 | 0.87 | 6 | 0.29 | −0.03 | 0.30 |
| 2 | 0.86 | 6 | 0.11 | −0.01 | −0.02 |
| 3 | 0.85 | 6 | 0.21 | 0.05 | 0.28 |
| 4 | 0.35 | 6 | 0.09 | −0.14 | 0.08 |
| 5 | 0.34 | 6 | −0.13 | 0.11 | −0.09 |
| 6 | 0.32 | 6 | −0.46 | −0.20 | −0.38 |
| 7 | 0.30 | 6 | −0.43 | −0.16 | −0.38 |
| 8 | 0.28 | 46 | 0.47 | 0.25 | 0.56 |
| 9 | 0.26 | 4 | 0.52 | 0.02 | 0.59 |
| 10 | 0.25 | 4 | 0.51 | −0.02 | 0.59 |
| 11 | 0.22 | 4 | −0.55 | −0.03 | −0.66 |
| 12 | 0.19 | 19 | −0.63 | −0.42 | −0.64 |
| 13 | 0.16 | 19 | 0.55 | 0.14 | 0.63 |
| 14 | 0.13 | 19 | −0.63 | −0.42 | −0.64 |
| 15 | 0.09 | 4 | 0.61 | 0.42 | 0.60 |
| 16 | 0.01 | 4 | −0.98 | −0.93 | −1.00 |
| 17 | 0.00 | 4 | 1.00 | 1.00 | 1.00 |
| 18 | 0.02 | 21 | 0.44 | 0.20 | 0.63 |
| 19 | 0.03 | 7 | −0.66 | −0.38 | −0.70 |
| 20 | 0.08 | 7 | −0.16 | −0.67 | 0.18 |
| 21 | 0.73 | 9 | 0.17 | 0.06 | 0.13 |
| 22 | 0.80 | 9 | 0.17 | 0.06 | 0.08 |
| 23 | 0.90 | 9 | 0.20 | 0.08 | 0.15 |
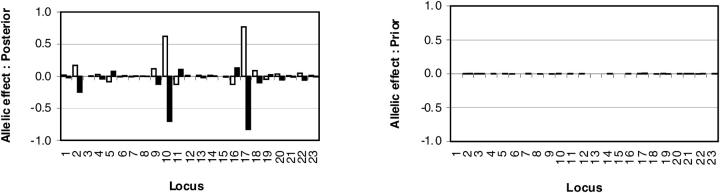
In Figure 3 (left), the posterior plot of estimated allelic effects consistently supported the same two markers (10 and 17) as indicated in Figure 2. One can see large and opposite effects of two alleles at these markers. The difference (or contrast) between these coefficients is comparable to the estimated effect obtained under the model where the first coefficient at each locus is constrained to zero. For comparison, the right side of Figure 3 shows allelic effects under the prior model (without data). Note that effect estimates shown in Figure 3 are point estimates (mean) whereas the whole distribution is summarized for loci 10 and 17 in Table 2.
Figure 3.—
QTL allelic effects. Locus-specific point estimates (mean) of allelic effects for the CF data set (left) and the corresponding prior (right) are shown. The first and the second allele at each marker locus are shown as open and solid bars, respectively. These quantities are calculated on the basis of pooling samples from two separate MCMC chains with 30,000 samples (after an initial 5000 burn-in rounds) in each. All sampled values were utilized in these estimates, including the iterations where the marker indicator was zero. Marker numbers are shown on the _x_-axis and the underlying hidden phenotype (liability) scale is on the _y_-axis. Note that the effects are double in size.
TABLE 2.
CF data
| Marker | Allele | Mean | SD | 2.5% | 97.5% |
|---|---|---|---|---|---|
| 10 | 1 | 0.62 | 0.89 | −1.35 | 2.20 |
| 2 | −0.70 | 0.91 | −2.31 | 1.36 | |
| 17 | 1 | 0.77 | 0.85 | −1.19 | 2.28 |
| 2 | −0.83 | 0.86 | −2.31 | 1.17 |
In general, effect estimation can be inaccurate in practice and as mentioned before, estimates for the QTL positions and their effects may be confounded. Therefore, a more robust way of analyzing association in such confounded models can be done by combining two sources of posterior information (QTL and their effects) into a single marker-specific summary that can be called a weighted genetic variance. This may be obtained from the posterior distribution of the product of indicator variable Il and either absolute difference (biallelic case) or variance (multiallelic case) of allelic effects β_la_'s at each location l. For biallelic loci, this summary corresponds to a model-averaged effect estimate (averaged over all models with the effect set to zero in models where the marker was not selected) proposed by Ball (2001) and a model-averaged variance estimate for multiallelic markers. However, for the present analysis, this practice produced a picture similar to Figure 2 (with an approximate scale difference). A related approach of combining posterior information on QTL and their effects using Bayesian QTL mapping and variance component models has been proposed in Xu and Yi (2000).
Linkage disequilibrium pattern due to close linkage of loci:
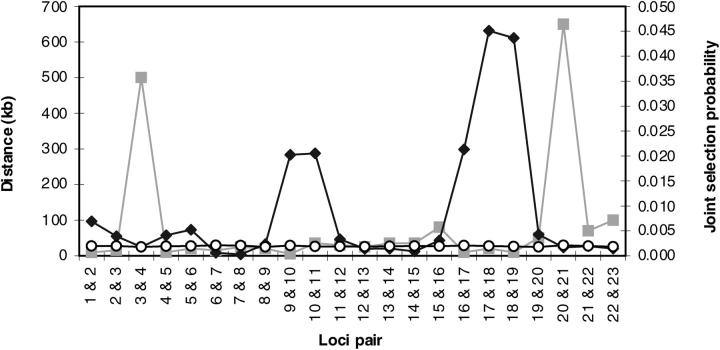
Instead of estimating LD as a degree of joint occurrence of alleles at two loci (which requires haplotype data), we assume that the effect of LD should also be visible in the behavior of locus indicators (in the case that they are not confounded; otherwise a weighted genetic variance may be selected). We express the strength of LD as a probability of an event that two adjacent markers have value one simultaneously in their locus indicators (this event is called joint selection). Figure 4 shows distinctly elevated posterior probabilities of joint selection around marker 17 and also around marker 10 (although not so high) compared to prior levels of LD.
Figure 4.—
Estimated linkage disequilibrium pattern for the CF data set. The posterior probabilities of jointly selecting two adjacent markers into the model (i.e., their indicators have value one simultaneously) are estimated for each marker pair (diamond, scale in the right _y_-axis). For each marker pair, the corresponding prior (circle, scale in the right _y-_axis) and the physical distance between markers are also shown (box, scale in the left _y_-axis). Markers present in each marker pair are shown on the _x_-axis.
Inference about estimated average age of mutations over trait loci:
Sometimes it may not be simple to parameterize the model to obtain a direct posterior of a certain quantity of interest analytically, as is the case here. To make inference about such a stochastic function of the posterior distribution, a sequential analysis can be carried out by using posterior samples generated by a first Bayesian analysis as data in a second Bayesian analysis. We performed such an additional analysis for a posterior sample of locus indicators to estimate the average age of mutations over trait loci. In this second Bayesian analysis, 30,000 MCMC samples were considered as actual data points consisting of sampled values of indicators xl = 1{_Il_=_Il_−1=1} for each consecutive marker pair (l − 1, l) among 23 markers. In our model we assumed that indicators xl are Bernoulli distributed with parameter e−adl, where a represents the average age of mutation over trait loci with a possible scale difference and dl is the distance between consecutive markers of marker pair (l − 1, l). We assumed a Gamma(5, 0.05) prior for age parameter a and ran two parallel chains with 3500 MCMC rounds (with 1000 burn-ins in each) resulting altogether in 5000 pooled MCMC samples to be utilized for estimation. The sampler seemed to have converged quickly. Note that although this model appears to be similar to the one used for smoothing, the smoothing parameter λ does not have this interpretation because it represents prior rather than posterior dependency (linkage disequilibrium) along a chromosomal segment.
In the analysis described above, the estimated posterior mean of age a was 0.2679. Because 1 cM is ∼1 Mb in humans and our analyses were performed in kilobases, we have to multiply our estimate by 1000, leading to an estimated age of 268 generations (with 95% credible interval [266, 269]). Others have found an estimated age of Δ_F_508 to be near 200 (Serre et al. 1990; Morris et al. 2000). However, recall that our estimate is averaged over all trait loci (positions 10 and 17) and does not represent only the CFTR region. Therefore, we did yet another analysis and allowed two age parameters, one for the CFTR region (markers 16–20) and another outside of it (models not shown). The new analysis resulted in posterior means of the two age parameters to be 207 (with 95% credible interval [205, 208]) at the CFTR region and 319 (with 95% credible interval [316, 321]) elsewhere (i.e., dominated by position 10). This result is also in agreement with the idea that position 10 may have protective influence because it is very likely that mutations with protective effects are older than others.
Sensitivity analyses:
To study sensitivity of the estimates of age of mutation a, we performed test trials assuming Gamma(5, 0.05), Gamma(1, 1), or Gamma(10, 0.1) prior for a. All priors led to the same posterior estimates, strongly supporting the estimated value.
The estimated posterior mean for the smoothing parameter λ was 100, corresponding closely to the prior mean. To check validity of this estimate we also used some other values for prior mean. These extra analyses resulted in the posterior means of smoothing parameter values, which corresponded strongly to the prior assumption, indicating that this quantity is very dependent on the prior choice. However, the posterior distributions of other parameters were not affected by the changes made to the prior for the smoothing parameter.
With CF data, we tested four different priors for allelic coefficients: N(0, 1), N(0, 10), N(0, 20), and N(0, 100). The change of prior had the largest influence on the convergence time but also increased variability at the mean level of posterior estimated allelic coefficients with increased variability (“flatness”) in the prior. Maximally a 2.5-fold change was observed in the estimated allelic coefficient by changing the prior. The influence was negligible to the absolute difference between coefficients. However, the same positions were supported in all cases. We also tested the influence of changing the prior for overall mean and the results were comparable.
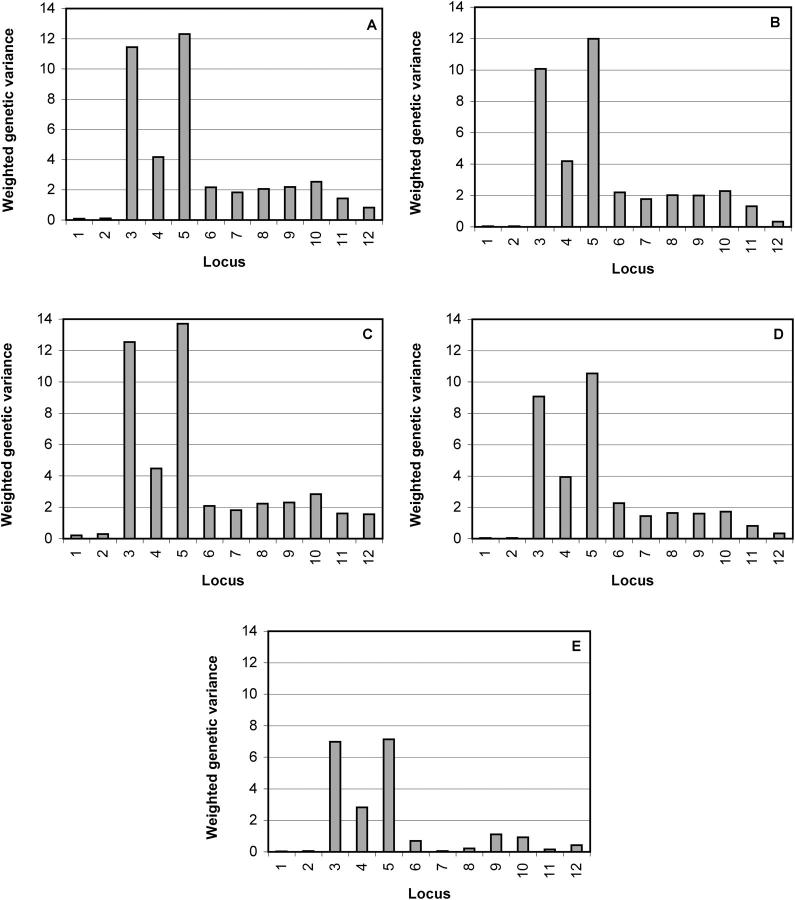
Friedrich ataxia data:
Unlike with CF data, locus-indicator variables turned out to be confounded with QTL effects in the Friedreich ataxia data (due to high LD). Therefore, we present posterior information on locus indicators and effect parameters in a combined form (weighted genetic variance). This quantity was calculated at each MCMC iteration as an indicator times genetic variance at a particular locus I l × σ2g_l_. In Figure 5, one can see the posterior mean weighted genetic variance estimated at different marker positions. Two putative QTL positions at markers 3 and 5 are clearly indicated. It is known that the gene is located between markers 5 and 6 (Liu et al. 2001). Note that the best putative candidate of Molitor et al. (2003a) was marker 3. Again we did some closer inspection of the haplotype data and found a striking joint occurrence of certain alleles at haplotypes of loci 3 and 5 among disease haplotypes (32/58 with haplotype 8-5 and 12/58 with haplotype 8-6) and to some extent also among control haplotypes (11/69 with haplotype 8-5 and 3/69 with haplotype 8-6; all results not shown). Joint occurrence among controls is not conclusive due to a high number of missing alleles at marker 5 (23/69). Simple odds ratio calculation for alleles indicates enrichment of alleles 3 and 5 of marker 5 and allele 8 of marker 3 among the cases with values 2.1, 2.3, and 2.5, respectively. However, allele 5 of marker 5 occurs together in haplotypes with allele 8 of marker 3. The same was further supported by the posterior estimates of individual allelic effects (results not shown). To conclude, most of the alleles that were estimated to be enriched among cases occurred jointly with a high frequency with either allele 3 of marker 5 or allele 8 of marker 3 (which also implies they occurred with alleles 5 or 6 of marker 5). Therefore all the enriched alleles of all markers could be approximately represented by these two alleles at these two markers together. This further supports two putative findings of this analysis.
Figure 5.—
Locus-specific point estimates (mean) of weighted genetic variances for the Friedreich ataxia data. Different types of specifications for smoothing parameter λ are shown: (A) wide Gamma(1, 0.01) prior for λ with mean 100 (posterior mean 62.65); (B) narrow Gamma(100, 1) prior for λ with mean 100 (posterior mean 99.32); (C) λ = 10 (strong smoothing); (D) λ = 250 (weak smoothing); and (E) independent prior for indicators with no λ parameter (no smoothing). Marker numbers are shown on the _x_-axis and weighted genetic variances are on the _y_-axis. Note that the variance parameter is for the model where the effects are double in size.
Figure 5 represents weighted genetic variance under different prior specifications for overall smoothing parameter λ and for locus indicators (each corresponding to a different level of smoothing). In Figure 5A one can see that if we assume a wide prior for the smoothing parameter, similarly as in the CF data, we obtain a moderately smoothed posterior. In contrast, if a narrow prior is given for the smoothing parameter (Figure 5B), we obtain a posterior where the smoothing has become a bit stronger (this is more visible in the estimated LD pattern, results not shown). By comparing Figure 5E (no smoothing), Figure 5D (weak constant smoothing), and Figure 5C (strong constant smoothing), one can clearly see that signals at positions 3 and 5 become stronger as levels of smoothing increase. Figure 5E corresponds to the model, where a priori independence of locus indicators was assumed [_cf._ the model of Kilpikari and Sillanpää (2003), where all unoccupied QTL positions were considered to be equally likely].
Dichotomizing transformation for weighted genetic variance:
Direct inference about estimated average age of mutations over trait loci or number of QTL, as was done for CF data, is not possible from FA data because the estimates of locus indicators and effects are confounded in the FA data due to high linkage disequilibrium. In other words, posterior weighted genetic variances clearly differ from posterior QTL probabilities. To estimate age of mutation (or number of QTL) under this condition, we transform each (continuous) weighted genetic variance to a binary form that can be called an adjusted locus indicator, which can then be collected together and plotted as QTL probabilities. The QTL-probability plot drawn from adjusted indicators should resemble the plot drawn from weighted genetic variances (with an approximate scale difference). These adjusted indicators (that are created by transformation) can then be used as data for estimating age of mutation over trait loci or number of QTL similar to our CF analysis.
To understand the transformation, let us first consider the marker-specific posterior for the weighted genetic variance. Note that only a single value (mean) of this posterior is plotted at each marker point in Figure 5. Although the histogram estimates indicate these variables to be stochastically ordered (for the FA data), in the absence of analytical forms (for these posteriors), we utilize only the tail-ordering property of the posteriors. For each marker, we estimated the corresponding tail probability of exceeding the predefined percentile of the joint distribution of all weighted genetic variances. [Alternatively, the cutoff point can be visually defined from the weighted genetic variance plot (Figure 5).] Mathematically this is a simple Bernoulli discretization of a continuous variable where the corresponding Bernoulli probability then represents the probability for a marker to have a high or extreme value of the weighted genetic variance. These tail probabilities should be similar in pattern (over markers) with those obtained by the means as in Figure 5. (Assuming the means to be reasonable estimates of the central tendency of the weighted genetic variances).
Estimated average age of mutations over trait loci and their number in FA data:
We performed several trials with different cutoff points put on the weighted genetic variance and each time ran the separate age estimation analysis with MCMC using adjusted locus indicators as data, as in CF analysis (results not shown). As expected, the estimated age depends on the stringency of the criteria used to define adjusted locus indicators. The higher the cutoff is put on the weighted genetic variance the rarer the event becomes and the estimated age would increase accordingly. However, even with the choice of cutoff as 90th, 95th, and 99th percentiles (of the overall distribution) the posterior (median) age estimates were 30, 42, and 66 generations (with narrow credible intervals), indicating this to be a recent mutation compared to many others. The corresponding three estimates for the number of QTL were 1.2, 0.6, and 0.1, respectively. Three percentiles correspond to points 7.85, 13.29, and 33.65, respectively, in the weighted genetic variance scale (recall that only means are shown in Figure 5). On the basis of these trials, it seems that this practice can provide useful information on the neighborhood of the age estimate rather than a unique estimate in such cases where direct estimation is impossible due to confounding. However, this practice is not very suitable for estimating the number of QTL.
Comparison of missing value imputation methods:
On the basis of our numerical experiments with these data sets, it was clear that missing data imputation that was applied to the FA data (with the prior where each allele was considered as equally likely) was better behaved than that in the CF data (with the Dirichlet prior for allele frequency hyperparameters), providing faster convergence.
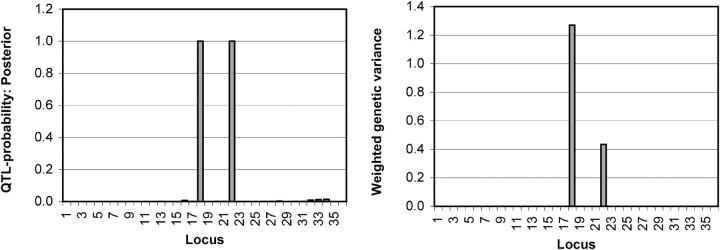
Simulated data:
As expected, in large genomic regions this model seems to behave in a closely similar fashion to the model of Kilpikari and Sillanpää (2003). In Figure 6 (left), one can see that the posterior QTL probability is practically zero at most of the markers (except some faint pattern due to LD) while it is one at true QTL locations (18 and 22). Recall that marker 25 showed a weak signal in Kilpikari and Sillanpää (2003), which we think is due to missing values in the analyzed data set. The same two positions (18 and 22) are supported also in Figure 6 (right), which presents weighted genetic variances for the data. Note that it is clearly visible that position 18 had a stronger effect than 22. The posterior (mean) estimate for the number of QTL in the whole region was 2. Closer inspection of locus indicators showed that some dependence between indicators was found only between markers 15–16 and 31–34, where the intermarker distances were the smallest (recombination fractions for the two regions were 0.02 and [0.02, 0.01, 0.01], respectively; results not shown).
Figure 6.—
Locus-specific estimates of QTL probabilities (left) and weighted genetic variances (right) for the simulated data set, where loci 18 and 22 represent the true gene locations. Marker numbers are shown on the _x_-axis and QTL probabilities/weighted genetic variances are on the _y_-axis.
DISCUSSION
We have presented a new multilocus method for association mapping in short chromosomal intervals, where covariances between markers are accounted for by using available physical or genetic distance information. Accounting for these covariances corresponds to spatial smoothing of association signals (LD measured from locus indicators) along the candidate region. The method is suitable for genotype data on multiallelic markers and is equally applicable for quantitative and binary traits and can handle some degree of missing observations. One can also estimate the age of the variant, which should be interpreted here as time to the most recent common ancestor rather than to actual age of mutation, which can be much older (Rannala and Slatkin 1998). One advantage of this method is that it can be implemented with WinBUGS (see Congdon 2001), which avoids user specification of data-specific tuning parameters needed in the Metropolis-Hastings random-walk algorithm (Chib and Greenberg 1995). Moreover, inclusion of covariate information (such as age, sex, or environmental risk factors) or dominance (genotype effects) into the phenotype model is straightforward in WinBUGS. However, the overall smoothing parameter λ can be thought of as a special tuning parameter in our model, which should not be too small in data sets with strong LD. With small values, the dependence between adjacent locus indicators may become too strong, practically preventing the MCMC sampler from moving (insufficient mixing). This may also happen with some prior distributions, which allow small values for λ. Therefore, one should be careful when analyzing data sets known to have strong LD.
We share the view of Phillips et al. (2003) and Morris et al. (2003b) that the block structure of LD in the human genome creates a need for sophisticated modeling to refine locations within the LD blocks. (For the opposite view, see Goldstein 2001.) Conti and Witte (2003) demonstrated how haplotype block information (Daly et al. 2001; Goldstein 2001; Gabriel et al. 2002; Wall and Pritchard 2003) can be easily incorporated in their model so that marker-specific gene effects “borrowed information” or were depending on each other only within the same block. The same goal (independence of markers between blocks) can be obtained in our model by artificially replacing the known distance between block-boundary markers (adjacent markers that are members in different blocks) with some arbitrarily large value corresponding to independence of loci. Utilization of block information corresponds to accounting for common population ancestry (LD due to covariance between haplotypes).
Population stratification is a well-known problem with association studies (Cardon and Palmer 2003). The benefit of the “LD smoothing” approach presented here is that it can control fluctuations in LD (spurious associations) due to several factors including events in population history. This way one does not need to apply matching (Hind et al. 2004) or utilize techniques such as genomic controls (Devlin and Roeder 1999) or structured association (Pritchard et al. 2000a,b; Sillanpää et al. 2001; Corander et al. 2003, 2004; Hoggart et al. 2003), which use an external set of unlinked markers. If the sample consists of related individuals with known relationships, inclusion of a polygenic component into the association model could take away a stratification problem completely (see discussion in Kilpikari and Sillanpää 2003). Available relationship information also enables the use of models that combine pedigree and linkage disequilibrium information (Meuwissen et al. 2002; Perez-Enciso 2003; Fan and Jung 2003; Lund et al. 2003; Meuwissen and Goddard 2004).
The postgenomic era is bringing us a vast amount of external public information on the human genome sequence. Rannala and Reeve (2001) proposed utilization of such information by specifying an informative prior distribution for the location of a disease gene in their Bayesian LD analysis. An informative prior providing information on gene-rich areas or distribution of exons and introns in the candidate region will improve gene localization. To utilize this type of external information in our model, one can modify the prior for locus-specific indicators p(Il|_Il_−1, s, λ, dl) by specifying individual values of shrinkage factor 1 − s at each locus, reflecting the prior probability of the position (locus-specific sl should then be scaled so that they sum up to the prior number of QTL in region R).
We want to briefly comment on our choice of a logit-link function here in contrast to a probit link that was used in Kilpikari and Sillanpää (2003). The logit link was chosen here because of its good mixing properties in WinBUGS (A. Thomas, personal communication). Additionally, although probit and logit-link functions are very close to each other, only logit link is robust for ascertainment (Kagan 2001; Neuhaus 2002). The choice of probit link, implemented via data augmentation, was motivated in Kilpikari and Sillanpää (2003) by the technical fact that one was able to apply exactly the same MCMC sampler (including the full conditionals) for all underlying model parameters in both quantitative and binary traits.
In some cases, the number of QTL-effect parameters (categories) considered in the model may become too large to model each parameter with a fixed-variance model (fixed-effect model). Such a situation may arise if the number of distinct alleles segregating in a marker is very high or one considers gene-gene or gene-environment interactions or genotype/haplotype-specific effects in the phenotype model. In an alternative to the random-variance model (“variance component model”), which avoids these problems, one can coarse the number of groups by regrouping alleles or genotypes/haplotypes into a small number of new groups on the basis of some simple rule. A more sophisticated solution is to include partitioning as a part of the model following ideas in Seaman et al. (2002).
Estimates for the number of QTL in studies, which concentrate on small chromosomal intervals, are confounded by strong LD (dependence) between markers. It is very likely that more than just a single marker is in strong LD with the true QTL and therefore they show elevated gene activity, as illustrated in CF and FA data. Because LD appears as continuous segments around the QTL due to common history, it may be more meaningful to estimate the number of QTL as the number of trait-associated marker segments rather than as the number of individual trait-associated markers (see Terwilliger et al. 1997; Chapman and Thompson 2002). The alternative, illustrated with FA data, to estimate the number of QTL from transformed data, did not seem to perform well. One potential future approach to reduce or better control confounding in our model would be to apply stochastic search variable selection (SSVS; George and McCulloch 1993; Yi et al. 2003; Meuwissen and Goddard 2004) so that locus indicators are hierarchically controlling the prior of QTL effects. A well-known drawback in SSVS is that it requires additional tuning parameters (pseudo-priors), which are data dependent (Dellaportas et al. 2000). In any case, the subset selection of candidate markers should be done by the analyst on the basis of the highly elevated locus-specific QTL probabilities or weighted genetic variances in contrast to selection based on markers showing small _P_-values in classical association testing. By doing so a Bayesian analysis avoids complicated problems in multiple testing. On the other hand, Bayesian analysis requires attention to monitoring of convergence and inspection of mixing properties of the MCMC sampler. Also so-called sensitivity analysis is an important part of good analysis practice.
We have put the model specification code (written in the BUGS language) at URL: http://www.rni.helsinki.fi/~mjs/. This code is freely available for research purposes.
Acknowledgments
We are grateful to Jules Hernández-Sánchez and Andrew Thomas for helpful discussions and two anonymous reviewers for comments that greatly improved the presentation of the results. This work was supported by a research grant (202324) from the Academy of Finland and by the Centre of Population Genetic Analyses, University of Oulu, Finland.
References
- Ball, R. D., 2001. Bayesian methods for quantitative trait loci mapping based on model selection: approximate analysis using Bayesian information criterion. Genetics 159**:** 1351–1364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertranpetit, J., and F. Calafell, 1996 Genetic and geographical variability in cystic fibrosis: evolutionary considerations, pp. 97–114 in Variation in the Human Genome, edited by D. Chadwick and G. Cardew. Wiley, Chichester, England. [DOI] [PubMed]
- Broman, K. W, and T. P. Speed, 2002. A model selection approach for identification of quantitative trait loci in experimental crosses. J. R. Stat. Soc. B 64**:** 641–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cardon, L. R., and L. J. Palmer, 2003. Population stratification and spurious allelic association. Lancet 361**:** 598–604. [DOI] [PubMed] [Google Scholar]
- Chapman, N. H., and E. A. Thompson, 2002. The effect of population history on the length of ancestral segments. Genetics 162**:** 449–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chib, S., and E. Greenberg, 1995. Understanding the Metropolis-Hastings algorithm. Am. Stat. 49**:** 327–335. [Google Scholar]
- Clayton, D., 2000. Linkage disequilibrium mapping of disease susceptibility genes in human populations. Int. Stat. Rev. 68**:** 23–43. [Google Scholar]
- Congdon, P., 2001 Bayesian Statistical Modelling. John Wiley & Sons, Chichester, UK.
- Conti, D. V., and J. S. Witte, 2003. Hierarchical modeling of linkage disequilibrium: genetic structure and spatial relations. Am. J. Hum. Genet. 72**:** 351–363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conti, D. V., V. Cortessis, J. Molitor and D. C. Thomas, 2003. Bayesian modeling of complex metabolic pathways. Hum. Hered. 56**:** 83–93. [DOI] [PubMed] [Google Scholar]
- Corander, J., P. Waldmann and M. J. Sillanpää, 2003. Bayesian analysis of genetic differentiation between populations. Genetics 163**:** 367–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corander, J., P. Waldmann, P. Marttinen and M. J. Sillanpää, 2004. BAPS 2: enhanced possibilities for the analysis of the genetic population structure. Bioinformatics 20**:** 2363–2369. [DOI] [PubMed] [Google Scholar]
- Cordell, H. J., and R. C. Elston, 1999. Fieller's theorem and linkage disequilibrium mapping. Genet. Epidemiol. 17**:** 237–252. [DOI] [PubMed] [Google Scholar]
- Daly, M. J., J. D. Rioux, S. F. Schaffer, T. J. Hudson and E. S. Lander, 2001. High-resolution haplotype structure in the human genome. Nat. Genet. 29**:** 229–232. [DOI] [PubMed] [Google Scholar]
- Dellaportas, P., J. J. Forster and I. Ntzoufras, 2000 Bayesian variable selection using the Gibbs sampler, pp. 273–286 in Generalized Linear Models: A Bayesian Perspective, edited by D. K. Dey, S. K. Ghosh and B. K. Mallick. Marcel Dekker, New York.
- Devlin, B., and K. Roeder, 1999. Genomic control for association studies. Biometrics 55**:** 997–1004. [DOI] [PubMed] [Google Scholar]
- Devlin, B., K. Roeder and L. Wasserman, 2003. Analysis of multilocus models of association. Genet. Epidemiol. 25**:** 36–47. [DOI] [PubMed] [Google Scholar]
- Durrant, C., K. T. Zondervan, L. R. Cardon, S. Hunt, P. Deloukas et al., 2004. Linkage disequilibrium mapping via cladistic analysis of single-nucleotide polymorphism haplotypes. Am. J. Hum. Genet. 75**:** 35–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan, R., and J. Jung, 2003. High-resolution joint linkage disequilibrium and linkage mapping of quantitative trait loci based on sibship data. Hum. Hered. 56**:** 166–187. [DOI] [PubMed] [Google Scholar]
- Flint, J., and R. Mott, 2001. Finding the molecular basis of quantitative traits: successes and pitfalls. Nat. Rev. Genet. 2**:** 437–445. [DOI] [PubMed] [Google Scholar]
- Gabriel, S. B., S. F. Schaffer, H. Nguyen, J. M. Moore, J. Roy et al., 2002. The structure of haplotype blocks in the human genome. Science 296**:** 2225–2229. [DOI] [PubMed] [Google Scholar]
- George, E. I., and R. E. McCulloch, 1993. Variable selection via Gibbs sampling. J. Am. Stat. Assoc. 88**:** 881–889. [Google Scholar]
- Gilks, W. R., A. Thomas and D. J. Spiegelhalter, 1994. A language and program for complex Bayesian modeling. Statistician 43**:** 169–178. [Google Scholar]
- Goldstein, D. B., 2001. Islands of linkage disequilibrium. Nat. Genet. 29**:** 109–111. [DOI] [PubMed] [Google Scholar]
- Greenland, S., J. A. Schwartzbaum and J. A. Finke, 2000. Problems due to small samples and sparse data in conditional logistic regression analysis. Am. J. Epidemiol. 151**:** 531–539. [DOI] [PubMed] [Google Scholar]
- Hind, D. A., R. P. Stokowski, N. Patil, K. Konvicka, D. Kershenobich et al., 2004. Matching strategies for genetic association studies in structured populations. Am. J. Hum. Genet. 74**:** 317–325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoggart, C. J., E. J. Parra, M. D. Shriver, C. Bonilla, R. A. Kittles et al., 2003. Control of confounding in genetic associations in stratified populations. Am. J. Hum. Genet. 72**:** 1492–1504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kagan, A., 2001. A note on the logistic link function. Biometrika 88**:** 599–601. [Google Scholar]
- Kerem, B.-S., J. M. Rommens, J. A. Buchanan, D. Markiewicz, T. K. Cox et al., 1989. Identification of the cystic fibrosis gene: genetic analysis. Science 245**:** 1073–1080. [DOI] [PubMed] [Google Scholar]
- Kilpikari, R., and M. J. Sillanpää, 2003. Bayesian analysis of multilocus association in quantitative and qualitative traits. Genet. Epidemiol. 25**:** 122–135. [DOI] [PubMed] [Google Scholar]
- Kuo, L., and B. Mallick, 1998. Variable selection for regression models. Sankhya Ser. B 60**:** 65–81. [Google Scholar]
- Lazzeroni, L. C., 1998. Linkage disequilibrium and gene mapping: an empirical least-squares approach. Am. J. Hum. Genet. 62**:** 159–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazzeroni, L. C., 2001. A chronology of fine-scale gene mapping by linkage disequilibrium. Stat. Methods Med. Res. 10**:** 57–76. [DOI] [PubMed] [Google Scholar]
- Liu, J. S., C. Sabatti, J. Teng, B. J. B. Keats and N. Risch, 2001. Bayesian analysis of haplotypes for linkage disequilibrium mapping. Genome Res. 11**:** 1716–1724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lund, M. S., P. Sorensen, B. Guldbrandtsen and D. A. Sorensen, 2003. Multitrait fine mapping of quantitative trait loci using combined linkage disequilibria and linkage analysis. Genetics 163**:** 405–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McPeek, M. S., and A. Strahs, 1999. Assessment of linkage disequilibrium by the decay of haplotype sharing, with application to fine scale genetic mapping. Am. J. Hum. Genet. 65**:** 858–875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen, T. H. E., and M. E. Goddard, 2000. Fine mapping of quantitative trait loci using linkage disequilibrium with closely linked marker loci. Genetics 155**:** 421–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen, T. H. E., and M. E. Goddard, 2004. Mapping multiple QTL using linkage disequilibrium and linkage analysis information and multitrait data. Genet. Sel. Evol. 36**:** 261–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen, T. H. E., B. J. Hayes and M. E. Goddard, 2001. Prediction of total genetic value using genome-wise dense marker maps. Genetics 157**:** 1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen, T. H. E., A. Karlsen, S. Lien, I. Olsaker and M. E. Goddard, 2002. Fine mapping of a quantitative trait locus for twinning rate using combined linkage and linkage disequilibrium mapping. Genetics 161**:** 373–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molitor, J., P. Marjoram and D. Thomas, 2003. a Fine-scale mapping of disease genes with multiple mutations via spatial clustering techniques. Am. J. Hum. Genet. 73**:** 1368–1384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molitor, J., P. Marjoram and D. Thomas, 2003. b Application of Bayesian spatial statistical methods to analysis of haplotypes effects and gene mapping. Genet. Epidemiol. 25**:** 95–105. [DOI] [PubMed] [Google Scholar]
- Morris, A., J. C. Whittaker and D. J. Balding, 2000. Bayesian fine-scale mapping of disease loci, by hidden Markov models. Am. J. Hum. Genet. 67**:** 155–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris, A., A. Pedder and K. Ayres, 2003. a Linkage disequilibrium assessment via log-linear modeling of SNP haplotype frequencies. Genet. Epidemiol. 25**:** 106–114. [DOI] [PubMed] [Google Scholar]
- Morris, A. P., J. C. Whittaker, C.-F. Xu, L. K. Hosting and D. J. Balding, 2003. b Multipoint linkage-disequilibrium mapping narrows location interval and identifies mutation heterogeneity. Proc. Natl. Acad. Sci. USA 100**:** 13442–13446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morton, N. E., W. Zhang, P. Taillon-Miller, S. Ennis, P.-Y. Kwok et al., 2001. The optimal measure of allelic association. Proc. Natl. Acad. Sci. USA 98**:** 5217–5221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuhaus, J. M., 2002. Bias due to ignoring the sample design in case-control studies. Aust. N. Z. J. Stat. 44**:** 285–293. [Google Scholar]
- Nordborg, M., and S. Tavare, 2002. Linkage disequilibrium: what history has to tell us. Trends Genet. 18**:** 83–90. [DOI] [PubMed] [Google Scholar]
- Perez-Enciso, M., 2003. Fine mapping of complex trait genes combining pedigree and linkage disequilibrium information: a Bayesian unified framework. Genetics 163**:** 1497–1510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips, M. S., R. Lawrence, R. Sachidanandam, A. P. Morris, D. J. Balding et al., 2003. Chromosome-wide distribution of haplotype blocks and the role of recombination hot spots. Nat. Genet. 33**:** 382–387. [DOI] [PubMed] [Google Scholar]
- Piepho, H.-P., and H. G. Gauch, Jr., 2001. Marker pair selection for mapping quantitative trait loci. Genetics 157**:** 433–444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard, J. K., M. Stephens and P. Donnelly, 2000. a Inference of population structure using multilocus genotype data. Genetics 155**:** 945–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard, J. K., M. Stephens, N. A. Rosenberg and P. Donnelly, 2000. b Association mapping in structured populations. Am. J. Hum. Genet. 67**:** 170–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rannala, B., and J. P. Reeve, 2001. High-resolution multipoint linkage-disequilibrium mapping in the context of a human genome sequence. Am. J. Hum. Genet. 69**:** 159–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rannala, B., and M. Slatkin, 1998. Likelihood analysis of disequilibrium mapping, and related problems. Am. J. Hum. Genet. 62**:** 459–473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risch, N., and K. Merikangas, 1996. The future of genetic studies of complex human diseases. Science 273**:** 1616–1617. [DOI] [PubMed] [Google Scholar]
- Sasieni, P. D., 1997. From genotypes to genes: doubling the sample size. Biometrics 53**:** 1253–1261. [PubMed] [Google Scholar]
- Seaman, S. R., S. Richardson, I. Stücker and S. Benhamou, 2002. A Bayesian partition model for case-control studies on highly polymorphic candidate genes. Genet. Epidemiol. 22**:** 356–368. [DOI] [PubMed] [Google Scholar]
- Sen, S., and G. A. Churchill, 2001. A statistical framework for quantitative trait mapping. Genetics 159**:** 371–387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serre, J. L., B. Simon-Bouy, E. Morret, B. Jaume-Roig, A. Balasso-poulou et al., 1990. Studies of RFLPs closely linked to the cystic-fibrosis locus throughout Europe lead to new consideration in population genetics. Hum. Genet. 84**:** 449–454. [DOI] [PubMed] [Google Scholar]
- Service, S. K., D. W. Lang, N. B. Freimer and L. A. Sandkuijl, 1999. Linkage-disequilibrium mapping of disease genes by reconstruction of ancestral haplotypes in founder populations. Am. J. Hum. Genet. 64**:** 1728–1738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sillanpää, M. J., and E. Arjas, 1998. Bayesian mapping of multiple quantitative trait loci from incomplete inbred line cross data. Genetics 148**:** 1373–1388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sillanpää, M. J., R. Kilpikari, S. Ripatti, P. Onkamo and P. Uimari, 2001. Bayesian association mapping for quantitative traits in a mixture of two populations. Genet. Epidemiol. 21**(Suppl. 1):** S692–S699. [DOI] [PubMed] [Google Scholar]
- Spiegelhalter, D. J., A. Thomas and N. G. Best, 1999 WinBUGS Version 1.2 User Manual. MRC Biostatistics Unit, Cambridge, UK.
- Tanksley, S. D., 1993. Mapping polygenes. Annu. Rev. Genet. 27**:** 205–233. [DOI] [PubMed] [Google Scholar]
- Terwilliger, J. D., W. D. Shannon, G. M. Lanthrop, J. P. Nolan, L. R. Goldin et al., 1997. True and positive peaks in genomewide scans: applications of length-biased sampling to linkage mapping. Am. J. Hum. Genet. 61**:** 430–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas, D., D. O. Stram, D. Conti, J. Molitor and P. Marjoram, 2003. Bayesian spatial modeling of haplotype association. Hum. Hered. 56**:** 32–40. [DOI] [PubMed] [Google Scholar]
- Uimari, P., and I. Hoeschele, 1997. Mapping linked quantitative trait loci using Bayesian analysis and Markov chain Monte Carlo algorithms. Genetics 146**:** 735–743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uimari, P., and M. J. Sillanpää, 2001. Bayesian oligogenic analysis of quantitative and qualitative traits in general pedigrees. Genet. Epidemiol. 21**:** 224–242. [DOI] [PubMed] [Google Scholar]
- Wall, J. D., and J. K. Pritchard, 2003. Haplotype blocks and linkage disequilibrium in the human genome. Nat. Rev. Genet. 4**:** 587–597. [DOI] [PubMed] [Google Scholar]
- Xu, S., 2003. Estimating polygenic effects using markers of the entire genome. Genetics 163**:** 789–801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu, S., and N. Yi, 2000. Mixed model analysis of quantitative trait loci. Proc. Natl. Acad. Sci. USA 97**:** 14542–14547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi, N., 2004. A unified Markov chain Monte Carlo framework for mapping multiple quantitative trait loci. Genetics 167**:** 967–975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi, N., V. George and D. B. Allison, 2003. Stochastic search variable selection for identifying multiple quantitative trait loci. Genetics 164**:** 1129–1138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yule, G. U., 1912. On the methods of measuring association between two attributes. J. R. Stat. Soc. 75**:** 576–642. [Google Scholar]