Soft Sweeps: Molecular Population Genetics of Adaptation From Standing Genetic Variation (original) (raw)

Abstract

A population can adapt to a rapid environmental change or habitat expansion in two ways. It may adapt either through new beneficial mutations that subsequently sweep through the population or by using alleles from the standing genetic variation. We use diffusion theory to calculate the probabilities for selective adaptations and find a large increase in the fixation probability for weak substitutions, if alleles originate from the standing genetic variation. We then determine the parameter regions where each scenario—standing variation vs. new mutations—is more likely. Adaptations from the standing genetic variation are favored if either the selective advantage is weak or the selection coefficient and the mutation rate are both high. Finally, we analyze the probability of “soft sweeps,” where multiple copies of the selected allele contribute to a substitution, and discuss the consequences for the footprint of selection on linked neutral variation. We find that soft sweeps with weaker selective footprints are likely under both scenarios if the mutation rate and/or the selection coefficient is high.

EVOLUTIONARY biologists envisage the adaptive process following a rapid environmental change or the colonization of a new niche in two contrasting ways. On the one hand, it is well known from breeding experiments and artificial selection that most quantitative traits respond quickly and strongly to artificial selection (see, e.g., Falconer and Mackay 1996). In these experiments, there is almost no time for new mutations to occur. Evolutionists who work with phenotypes therefore tend to hold the view that also in natural processes a large part of the adaptive material is not new, but already contained in the population. In other words, it is taken from the standing genetic variation. Consequently, standard predictors of evolvability, such as the heritability, the coefficient of additive variation, or the G matrix, are derived from the additive genetic variance of a trait; cf., e.g., Lande and Arnold (1983), Houle (1992), Lynch and Walsh (1998), and Hansen et al. (2003); see Steppan et al. (2002) for review. On the other hand, in the molecular literature on the adaptive process and on selective sweeps adaptation from a single new mutation is clearly the ruling paradigm (e.g., Maynard Smith and Haigh 1974; Kaplan et al. 1989; Barton 1998; Kim and Stephan 2002). In conspicuous neglect of the quantitative genetic view, the standing genetic variation as a source for adaptive substitutions is generally ignored, with only few recent exceptions (Orr and Betancourt 2001; Innan and Kim 2004).

The difference that is expressed in these two views could have important evolutionary consequences. If adaptations start out as new mutations the rate of the adaptive process is limited by the rates and effects of beneficial mutations. In contrast, if a large part of adaptive substitutions derives from standing genetic variation, the adaptive course is modulated by the quality and amount of the available genetic variation. Because this variation is shaped by previous selection, the future course of evolution will depend not only on current selection pressures, but also on the history of selection pressures and environmental conditions that the population has encountered. Clearly, quite different sets of parameters could be important under the two scenarios if we want to estimate past and future rates of evolution. To assess which alternative is more prevalent in nature, population genetic theory can be informative in two ways. First, it allows us to determine the probabilities for selective adaptations in both scenarios. Second, theory can be used to predict whether and how these different modes of adaptation can be detected from population data. In this article, we address these issues in a model of a single locus.

We study the fixation process of an allele that is beneficial after an environmental change, but neutral or deleterious under the previous conditions. The population may experience a bottleneck following the shift of the environment. Assuming that the allele initially segregates in the population at an equilibrium of mutation, selection, and drift, we calculate the probability that it spreads to fixation after positive selection begins. We compare this probability with the fixation rate of the same allele, given that it appears after the environmental change only as a new mutation. This allows us to determine the parameter space, in terms of mutation rates, selection coefficients, and the demographic structure, where a substitution that is observed some time after an environmental change is most likely from the standing genetic variation. We also analyze how the distribution of the effects of adaptive substitutions changes if the standing genetic variation is a source of adaptive material. Our main finding is that adaptations with a small effect in this case are much more frequent than predicted in a model that considers only adaptations from new mutations.

We then ask whether adaptations from standing genetic variation can be detected from the sweep pattern on linked neutral variation. If a selective sweep originates from a single new mutation, all ancestral neutral variation that is tightly linked to the selected allele will be eliminated by hitchhiking. We call this scenario a hard sweep in contrast to a soft sweep where more than a single copy of the allele contributes to an adaptive substitution. The latter may occur if the selected allele is taken from the standing genetic variation, where more than one copy is available at the start of the selective phase, or if new beneficial alleles occur during the spread to fixation. With a soft sweep, part of the linked neutral variation is retained in the population even close to the locus of selection. We calculate the probability for soft sweeps under both scenarios of the adaptive process and discuss the impact on the sweep pattern. We find that soft sweeps are likely for alleles with a high fixation probability from the standing variation, in particular for alleles that are under strong positive selection. Already for moderately high mutation rates, however, fixation of multiple independent copies is also likely if the selected allele enters the population only as a recurrent new mutation. We therefore predict that unusual sweep patterns compatible with soft sweeps may be frequent under biologically realistic conditions, but they cannot be used as a clear indicator of adaptation from standing genetic variation.

MODEL AND METHODS

Assume that a diploid population of effective size _N_e experiences a rapid environmental shift at some time T that changes the selection regime at a given locus. We consider two alleles (or classes of physiologically equivalent alleles) at this locus, a and A. a is the ancestral “wild-type” allele and A is derived, in the sense that the population was never fixed for A prior to T. A is favorable in the new environment with homozygous fitness advantage _s_b. The dominance coefficient is h; i.e., the heterozygous fitness is 1 + _hs_b. Assuming that the population was well adapted in the old environment, A was either effectively neutral or deleterious before T, with selection coefficient s_d measuring its homozygous disadvantage and dominance coefficient h_′. A is generated from a by recurrent mutations at rate u. In the following, it is convenient to work with scaled variables for selection and mutation, defined as αb = 2_N_e_s_b, αd = 2_N_e_s_d, and Θ_u = 4_N_e_u. We initially assume that the population size _N_e stays constant over the time period under consideration, but relax this condition later. We restrict our analysis to a single adaptive substitution, which is studied in isolation. This assumption means that different adaptive events do not interfere with each other due to either physical linkage or epistasis.

Simulations:

We check all our analytical approximations by full-forward computer simulations. For this, a Wright-Fisher model with 2_N_e haploid individuals is simulated. Every generation is generated by binomial or multinomial sampling, where the probability of choosing each type is weighted by its respective fitness. No dominance is assumed (h = h_′ = 0.5) and 2_N_e is 50,000. Data points are averaged over at least 12,000 runs for Θ_u = 0.4 and all data points in Figure 6, 20,000 runs for Θ_u_ = 0.04, and 40,000 runs for Θ_u_ = 0.004.

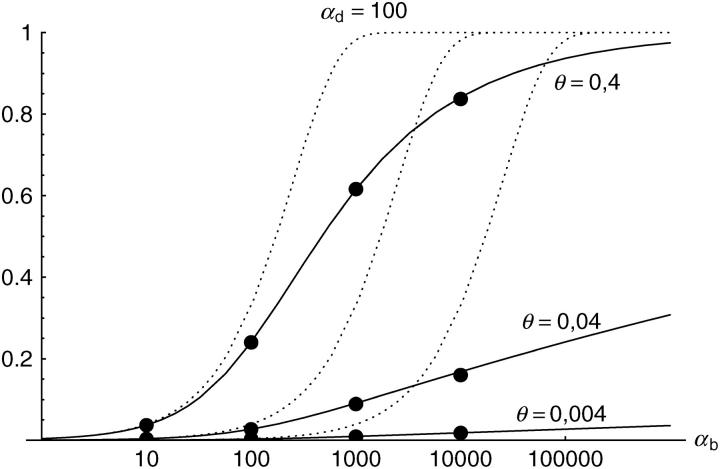
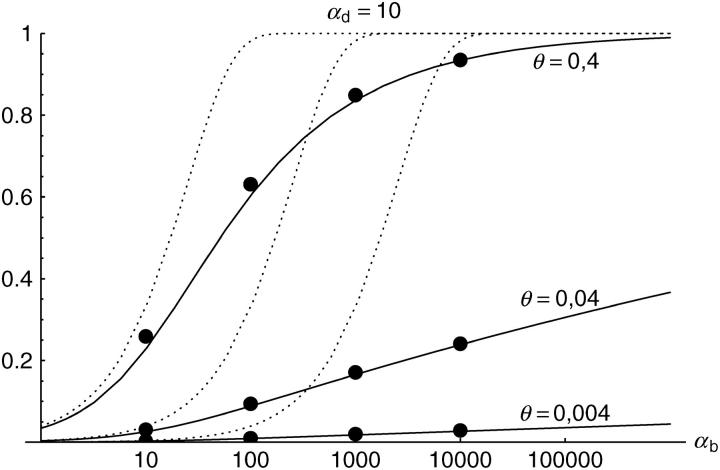
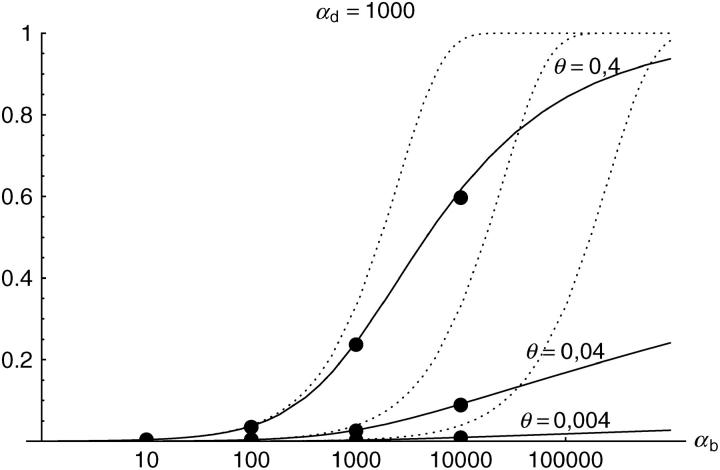
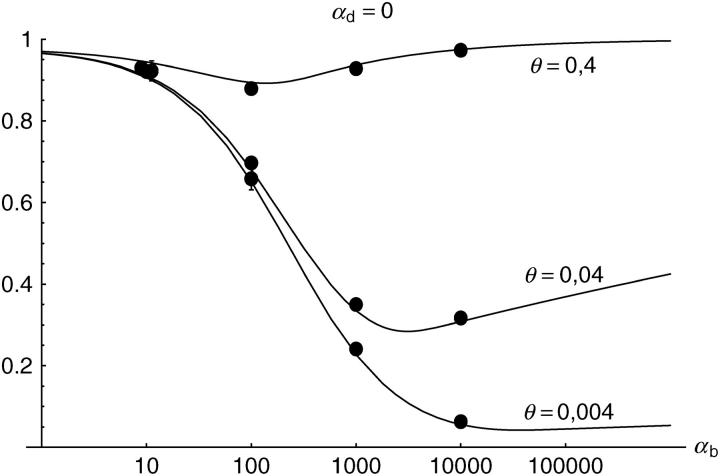
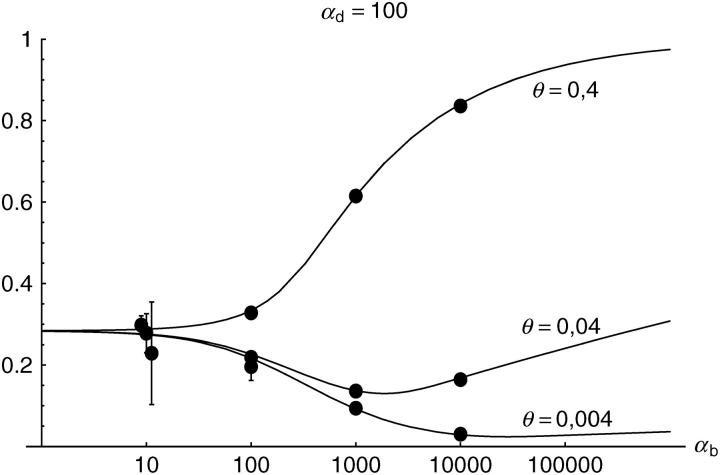
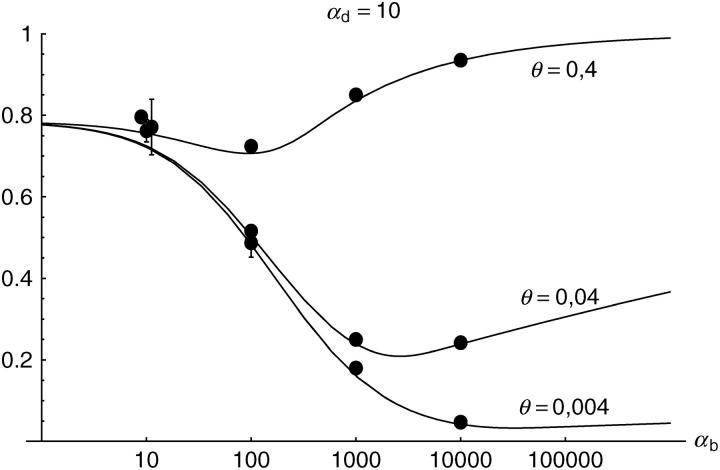
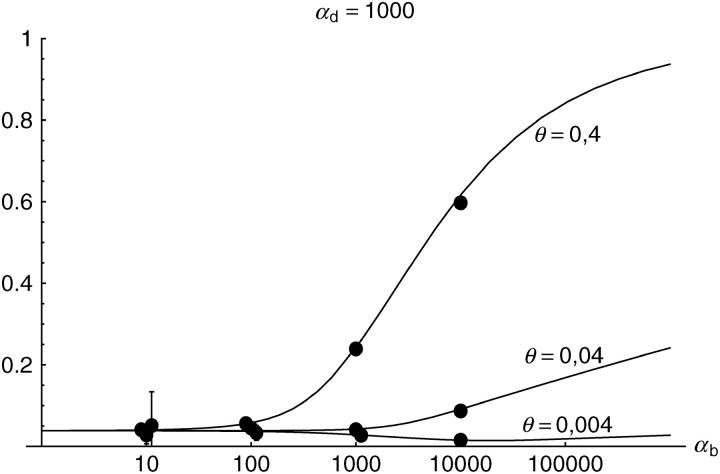
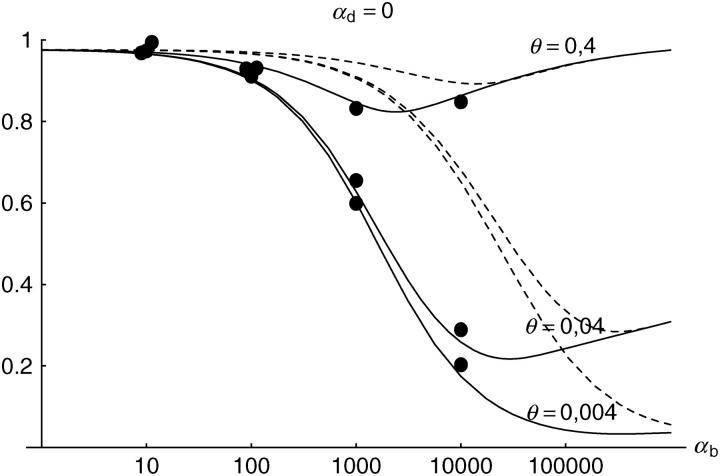
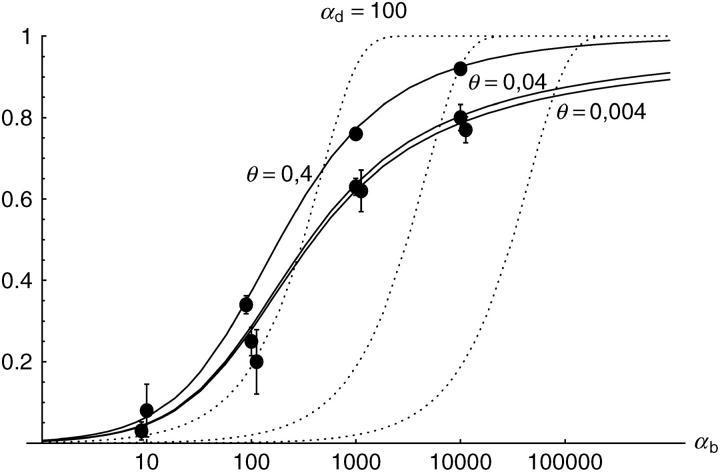
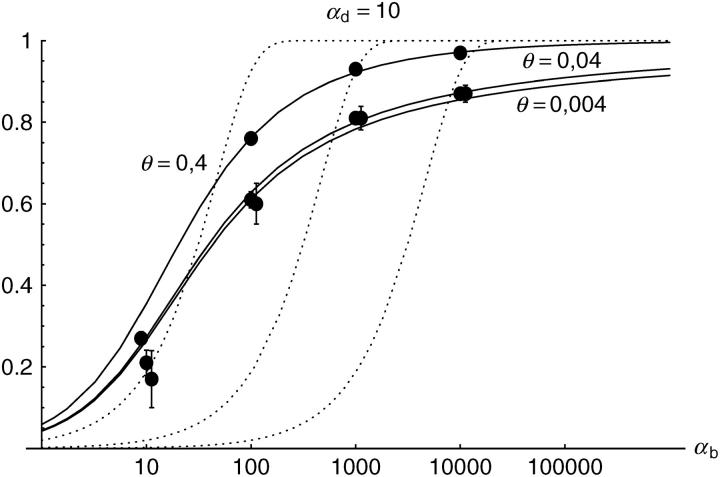
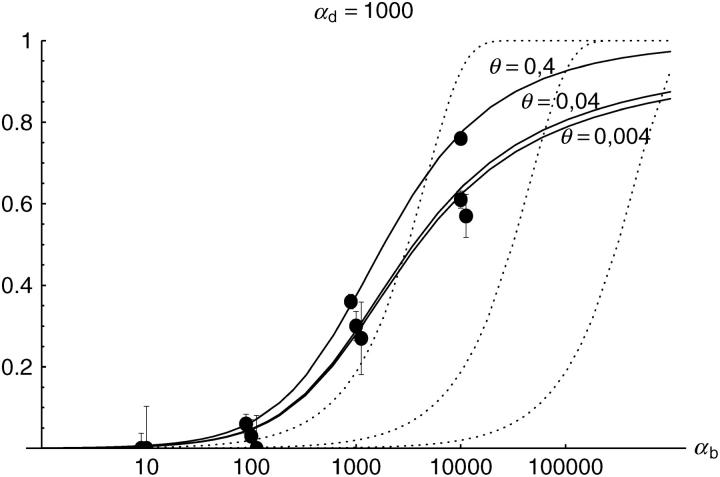
Figure 6.—

The probability that multiple copies with independent origin contribute to a substitution, _P_ind. Lines correspond to Equation 20; symbols represent simulation data. Circles represent fixations from the standing genetic variation without new mutational input after time T; squares include new mutations. Triangles represent fixations from recurrent new mutations only.

Each simulation is started 6_N_e = 150,000 generations before time T to let the population reach mutation-selection-drift equilibrium. Longer initial times did not change the results in trial runs. At the start, the population consists of only ancestral alleles “0”; the derived allele “1” is created by mutation. Whenever the derived allele reaches fixation by drift, it is itself declared “ancestral”; i.e., the population is set back to the initial state.

After 6_N_e generations, the selection coefficient of the derived allele changes from neutral or deleterious (_s_d) to beneficial (_s_b). Mutations now convert ancestral alleles into new derived alleles (using a different symbol, “2”) with the same selection coefficient _s_b. Simulations continue until eventual loss or fixation of the ancestral allele, where new mutational input is stopped G = 0.1_N_e = 2500 generations after the environmental change. Each run has four possible outcomes: Fixation of 0, 1, or 2 or of 1 and 2 together.

Bottleneck:

In the bottleneck scenario, the population is reduced to 1% at time T (NT = 250). After time T, the population is allowed to recover logistically following Nt+1 = Nt + rNt(1 − Nt/K), where r = 5.092 × 10−2 and the carrying capacity is K = 2546. This results in an average population size of N_av = 2500 (10% of the original size) after the environmental change until new mutational input is stopped at G = 0.1_N_e generations. For Θ_u = 0.004 only realizations with >10 fixation events in 40,000 runs are included in the numbers.

Number of (independent) copies:

To determine the number of independent copies that contribute to a fixation, each mutation is given a different name and followed separately. Runs are done with and without new mutational input after the environmental shift and continued until fixation of the selected allele or all copies from the standing variation are lost. Additionally, also runs with only new mutations are done. When fixation of the selected allele occurs, we count the number of descendants from different origins in the population. A similar procedure is followed to determine the number of copies from the standing variation that contribute to a substitution. For this, all copies of the selected allele that are present at the time of the environmental change are given a different name. In the case of fixation, the number of different copies in the population is counted. Only realizations with >10 fixations are included in the numbers.

RESULTS

Fixation probability from the standing genetic variation:

The fixation probability of an allele A with selective advantage _s_b that segregates in a population at frequency x is given by Kimura's diffusion approximation result:

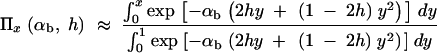	1

(Kimura 1957). In the following, we assume that selection on the heterozygote is sufficiently strong (formally, we need 2_h_αb ≫ (1 − 2_h_)/2_h_). We can then ignore the term proportional to y_2 in Equation 1 and Π_x is approximately

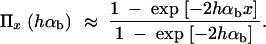	2

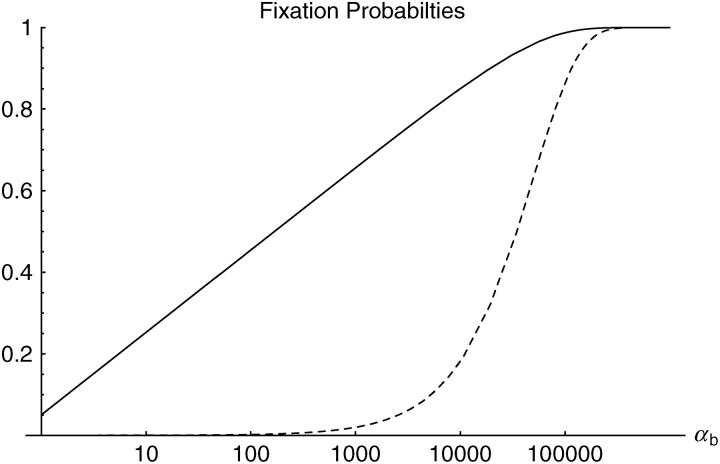
If A enters the population as a single new copy, x = 1/2_N_e, and if 2_N_e ≫ 2_h_αb ≫ 1, we recover Haldane's classic result that the fixation probability is twice the heterozygote advantage, Π1/2_N_e ≈ 2_hs_b (Haldane 1927). This relation underlines the importance of genetic drift: It is not sufficient for an advantageous allele to arrive in a population, it also needs to escape stochastic loss. Due to the strong linear dependence of the fixation probability on the selection coefficient, alleles with a small beneficial effect are less likely to escape such loss. The fixation process thus acts like a stochastic sieve that favors adaptations with large effects. This was stressed in particular by Kimura (1983). According to Equation 2, an approximately linear dependence of Π_x_ on _h_αb holds more generally as long as either the initial frequency x or the heterozygote advantage h_αb is small, such that 2_h_αb_x < 1.

Let us now compare this view of the fixation process with the alternative scenario of adaptation from the standing genetic variation. In the most simple case, the allele A again originates from a single mutation, but before the environmental change, and already segregates in the population under neutrality when positive selection sets in. Standard results (e.g., Ewens 2004) show that under these conditions the probability for an allele to segregate at a given frequency is proportional to the inverse of the frequency, 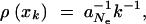where xk = _k/_2 _N_e and 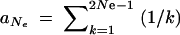. The average fixation probability is then 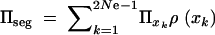. We derive an exact result for Πseg in terms of a hypergeometric function in the appendix; for 2_N_e ≫ 2_h_αb ≫ 1 we obtain the approximation

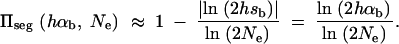	3

We can make two interesting observations from this result. First, as is seen in Figure 1, there is a large increase in the (average) fixation probability if an allele does not arise as a single new copy, but already segregates in the population. This increase is particularly large for small adaptations, which points to the second observation: For alleles from the standing genetic variation, the fixation probability depends only weakly (logarithmically) on the selection coefficient. Indeed, Πseg, unlike Π_x_, does not show a linear dependence on _h_αb even if _h_αb is very small. The reason is that, conditioned on later fixation, the average frequency of the allele at the time of the environmental change, 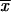k, increases with decreasing _h_αb, such that 2_h_αb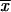k > 1 for all h_αb [a simple calculation in the appendix reveals that 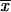k ≈ 1/ln2_h_αb]. The usual linear approximation of Π_x is therefore never appropriate.

Figure 1.—

Fixation probabilities from a single new mutation (dashed line) and from a single segregating allele (solid line). Note that αb is measured on a logarithmic scale.

Consider, now, an allele A that segregates in the population at an equilibrium of mutation, (negative) selection, and drift when the environment changes at time T. For t > T, positive selection sets in. We are interested in the net probability _P_sgv that the allele is available in the population at time T and subsequently goes to fixation. In the continuum limit for the allele frequencies, _P_sgv is given by the integral

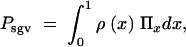	4

where Π_x_ is the fixation probability (Equation 2) and ρ(x) is the density function for the frequency of a derived allele in mutation-selection-drift balance. Approximations for ρ(x) can be obtained from standard diffusion theory; all derivations are given in the appendix. In the neutral case (αd = 0) the distribution of derived alleles is approximately

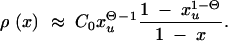	5

For a previously deleterious allele and 2_h_′αd ≫ (1 − 2_h_′)/2_h_′, we obtain

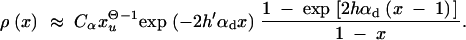	6

_C_0 and C_α are normalization constants. ρ(x) includes a probability Pr0 that A is not present in the population at time T. For Θ_u < 1, this probability is approximately

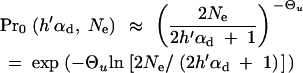	7

For the probability that the population successfully adapts from the standing variation we derive the simple approximation

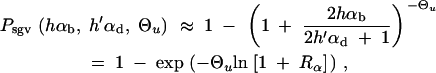	8

where R_α := 2_h_αb/_(2_h_′αd + 1) is the relative selective advantage. _R_α measures the selective advantage of A in the new environment relative to the forces that cause allele frequency changes in the ancestral environment, deleterious selection and drift (represented by the 1). We refer to _R_α < 1 and _R_α > 1 as cases of small and large relative advantage, respectively. If the allele A is completely recessive in the old environment (_h_′ = 0), similar approximations hold here and below if 2_h_′αd + 1 in R_α is formally replaced by 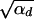+ 1 (see again the appendix for details). To relate Equation 8 to Equation 3, we need to calculate the fixation probability for a segregating allele that is derived from a single mutation prior to the environmental change. This probability is obtained from (8) and (7) by conditioning on segregation of the allele in the limit Θ_u → 0. We find

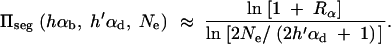	9

For αd = 0 and _h_αb ≫ 1 this reduces to Equation 3.

All further results of our study depend on Equation 8. Computer simulations show that this simple analytical expression is quite accurate over a large parameter range (assuming Θ_u_ < 1 and _h_αb, _h_′αd ≪ 2_N_e; see Figure 2). Slightly better approximations (which coincide with 95% confidence intervals of all our simulation runs) can be obtained by numerical integration of Equation 4, using the allele frequency distributions Equations 5 and 6. It is instructive to compare the stochastic result, Equation 8, with the deterministic approximation used by Orr and Betancourt (2001). If we set x ≡ Θ_u/_2_h_′αd in Equation 2 (the equilibrium value at mutation-selection balance), the fixation probability from the standing variation becomes

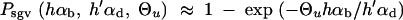	10

Equation 8 reduces to Equation 10 if and only if there is relatively strong past deleterious selection such that R_α ≪ 1. In this limit, the initial frequency of the selected allele is sufficiently reduced that the fixation probability Π_x (Equation 2) is approximately linear in x over the range of ρ(x), Π_x_ ≈ 2_h_αb_x_. In the integral (4) then only the average allele frequency 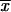enters, which (almost) coincides with the deterministic approximation. For R_α ≥ 1, the distribution ρ(x) feels the concavity of Π_x and the true value of _P_sgv drops below the deterministic estimate. This is captured by Equation 8; see Figure 2. For R_α ≤ 1 the fixation probability does not approach the “deterministic” approximation even if N_e and thus αd, αb, and Θ_u get large. The reason is that it is the variance of 2_h_αb_x that matters, which does not go to zero even if the variance of the allele frequency Var[x_] → 0 for large Θ_u and αd.

Figure 2.—

The probability of fixation from mutation-selection-drift balance, _P_sgv, for a range of mutation and selection parameters. Solid lines show approximation Equation 8 and dotted lines show the deterministic approximation Equation 10. Solid circles are simulation results. Ninety-five percent confidence intervals are contained in the circles.

Equations 8 and 9 confirm a weak dependence of the fixation probability on αb. For fixed αd, the fixation probability depends logarithmically on αb (and on _R_α) as long as _R_α > 1. In the “deterministic limit” _R_α ≪ 1, this dependence goes back to linear. However, this is true only if αb varies independently of αd. If stronger selected alleles have larger trade-offs, i.e., αb and αd are positively correlated, _R_α and thus _P_sgv and Πseg will increase less than linearly with αb even if _R_α ≪ 1. Using the deterministic aproximation, Orr and Betancourt (2001) previously found that the dominance coefficient drops out of _P_sgv if dominance does not change upon the environmental shift, h = _h_′. The stochastic result Equation 8 confirms this finding and extends it beyond the limits of validity of the deterministic approximation as long as _h_αb and _h_′αd are both large.

Standing variation vs. new mutations:

We want to compare the fixation probability from the standing variation with the probability that an adaptive substitution occurs from new mutation. The probability for a new allele to occur in the population that is destined for fixation is ∼_p_new = 2_N_e_u_2_hs_b per generation. Using a Poisson approximation, the probability that such a mutation arrives within G generations is

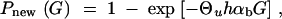	11

where G is measured in units of 2_N_e. We can now determine the number of generations _G_sgv that it takes for _P_new(_G_sgv) = _P_sgv. This value serves as a measure of the relative adaptive potential of the standing variation. Using Equation 8 we obtain

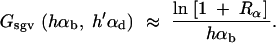	12

This value is independent of Θ_u_ and depends only on the selection parameters of the allele. One can relate _G_sgv to the average fixation time _t_fix of an allele with selective advantage _h_αb. In the appendix, we derive _t_fix in units of 2_N_e,

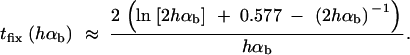	13

The approximation is very accurate for h = 0.5 and _h_αb ≳ 2. For h ≠ 0.5 it defines a lower bound. We see that _G_sgv < _t_fix for arbitrary _R_α. This holds even if we account for the fact that the average fixation time from the standing variation may be shorter (but ≥ t_fix/_2), since the allele starts at a higher frequency. This result means that in a time span that an allele from the standing variation needs to reach fixation, it is at least as likely that the allele alternatively appears as a new mutation destined for fixation only after the environmental change.

Next, we consider the case that a derived beneficial mutation A is found in a population some time after the environmental change. There are three possibilities: A derives from the standing genetic variation at time T, or from new mutation(s) that occurred after the environmental change, or both. Computer simulations that include new mutations after time T show that hybrid fixations that use material from both sources are quite frequent for high Θ_u_, but also that the contribution of the standing variation generally dominates in this case (for Θ_u_ = 0.4 on average 67–97%, depending on αb and αd). In the following, we combine hybrid fixations with fixations that use only alleles from the standing variation and define _P_sgv more broadly as the probability that an adaptive substitution uses material from the standing genetic variation. With this definition, simulation results are closely matched by the theoretical prediction in Equation 8.

We can now ask for the probability that a derived allele A, which is found in the population some time G after T, and either fixed or destined to go to fixation at this time, originated (at least partially) from alleles in the standing genetic variation. Measuring G in units of 2_N_e generations, this probability may be expressed as Prsgv = P_sgv/_(_P_sgv + (1 − _P_sgv)_P_new). With Equation 8,

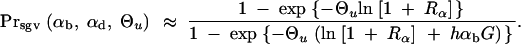	14

In Figure 3, this is shown for G = 0.05, i.e., for a time of 0.1_N_e generations after the environmental change. This time should be sufficiently long for significant adaptive change, but still short enough for a selective sweep to be detected in DNA sequence data (Kim and Stephan 2000; Przeworski 2002). For Drosophila melanogaster, 0.1_N_e generations approximately correspond to the time since it expanded its range out of Africa into Europe after the last glaciation (i.e., ∼10,000–15,000 years ago).

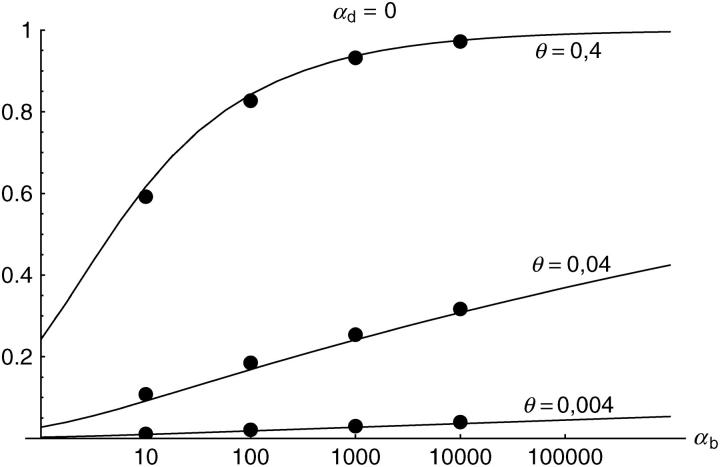
Figure 3.—

The probability that an adaptive substitution is from the standing genetic variation (Prsgv). Simulation data with 95% confidence intervals are compared to the analytical approximation Equation 14.

There are two advantages of the standing variation over adaptations purely from new mutations. First, the standing genetic variation may already contain multiple copies of the later-beneficial allele, reducing the probability of a stochastic loss relative to a single copy. This advantage is measured in the relative adaptive potential _G_sgv above. A second, independent advantage is that alleles from the standing variation are immediately available and may outcompete new mutations due to this head start. Consequently, we see that substitutions from the standing variation dominate in two parameter regions. First, they dominate for small _h_αb as long as selection before the environmental change was also weak because _P_sgv > _P_new in this range. (_P_sgv > _P_new for _h_αb < ln[1 + _R_α]/G; for small _h_αb this needs _h_′αd < 1/G, i.e., αd < 40 for _h_′ = 0.5 and G = 0.1_N_e.) The second parameter region is if h_αb and the mutation rate Θ_u are both high. In this case, the crucial advantage of the alleles from the standing genetic variation is their immediate availability: The probability for fixation from the standing variation is already sufficiently high that there is no need to wait for a new mutation to occur.

For practical application of this result, remember that Prsgv does not count only alleles that are fixed at time T + G, but also alleles that are destined to go to fixation. Consequently, simulations in Figure 3 are continued until loss or fixation of the allele even beyond T + G. This makes almost no difference as long as the average fixation time _t_fix of an allele is much smaller than G. However, if _t_fix ≥ G, Equation 14 can no longer be used to predict full substitutions. For G = 0.1_N_e, _t_fix > G if _h_αb ≲ 275. If we count only substitutions that are completed at time T + G, _P_new is more strongly reduced than _P_sgv. For alleles with _t_fix ≈ G, predominance of the standing genetic variation is larger than that predicted by Equation 14 (confirmed by simulations, results not shown). For alleles with _t_fix ≫ G practically all substitutions that are completed at time T + G contain material from the standing variation; however, there are then only very few fixations at all.

Population bottlenecks:

So far, we have assumed that the effective population size before, during, and after the environmental change is constant. For many evolutionary scenarios, however, it may be more realistic to assume that the shift of the environmental conditions is accompanied by a population bottleneck. Examples include colonization events and human domestication, but also the (temporary) reduction of the carrying capacity of a maladapted population in a changed environment.

Suppose that a population of ancestral size _N_0 goes through a bottleneck directly after the environmental change and recovers afterward until it reaches its carrying capacity in the new environment. We want to know how these demographic events change the probability Prsgv that a substitution is derived from the standing genetic variation. We expect two factors to play a role. On the one hand, a deep and long-lasting bottleneck may significantly reduce the standing variation and the potential of the population to adapt from it. On the other hand, a slow or incomplete recovery reduces the opportunity for new mutations to arrive in the population and thus the probability of adaptation from new mutations.

It is therefore instructive to distinguish two elements of a bottleneck, population size reduction and subsequent recovery, and discuss their effects separately. The simplest case is a pure reduction of N_0 by a factor B > 1 at time T, with no recovery. For matters of comparison, we continue to use the ancestral population size N_0 in the definitions of Θ_u, αb, αd, and G. In our formulas for the fixation probabilities from new or standing variation (Equations 8, 11, and 14) population size reduction is then simply included by a rescaling of the selection parameter αb to αb/B_. (For adaptations from the standing genetic variation note that a sampling step to generate a bottleneck does not change the frequency distribution of the later-beneficial allele, leaving αb in Equation 2 the only parameter subject to change. For adaptation from new mutations the rescaling argument follows if we express the probability for a new mutation destined for fixation per generation as p_new = (2_N_e/B_)u_2_hs_b = 2_uh_αb/B_.) Consequently, the graphs in Figure 3 are simply shifted to the right. A pure reduction of the population size at time T thus reduces the relative advantage of the standing genetic variation for strongly selected alleles with a large mutation rate, but enhances its advantage for weakly selected alleles. Note that the adaptive potential _G_sgv increases by a factor of B relative to _t_fix and can now be much larger than the fixation time.

Relative to a simple reduction in population size, recovery increases the adaptation probability from the standing variation, _P_sgv, and from new mutations, _P_new, in different ways. First, recovery increases _P_new (but not _P_sgv) simply due to the fact that the opportunity for new mutations increases with increasing population size. Second, the fixation probability of beneficial alleles is increased due to population growth. For further progress, we use results on the fixation probability in populations of changing size by Otto and Whitlock (1997). We assume that the population experiences logistic growth according to dN/dt = λ(1 − N/K)N after an initial reduction to NT. Here, λ is the intrinsic growth rate (for t in units of 2_N_0), and K the carrying capacity. There are two things to note. First, the effect of recovery on the fixation probability is significant only if it is sufficiently fast on a scale set by the selection strength. For logistic recovery, this is the case if λ ≳ _h_αb. Second, the increase of the fixation probability due to recovery is much more important for _P_sgv than for _P_new. The reason is that only alleles that are already present during the bottleneck will be affected. While this is the case for all alleles from the standing variation that survive population size reduction, only relatively few new mutations will occur in the small bottleneck population (at least if recovery is sufficiently fast to matter). More formally, one can show that the increase in the fixation probability due to recovery can be neglected in P_new if λ_G ≫ 1. This leaves only a very restricted parameter space of _h_αb ≲ λ ≲ 1/G, where an increase in fixation probability plays a role for _P_new (confirmed by simulations, not shown).

In the following, we concentrate on fast recovery on a scale of G, i.e., λ ≫ 1_/G_ (results for slow recovery are intermediate between fast and no recovery). As a measure for the opportunity for new beneficial mutations to arrive in the population, let _N_av be the average population size from time T to time T + G, where the substitutions are censused. We then define a bottleneck parameter for new mutations B_new := N_0/N_av and rescale αb to αb/B_new in _P_new (Equation 11). For fixations from the standing genetic variation, we define the bottleneck strength as _B_sgv(_h_αb) = N_0/N_fix(_h_αb) and rescale the relative selection strength _R_α → R_α/B_sgv in Equations 8 and 14. Here, _N_fix is an average “fixation effective population size” that is felt by a beneficial allele on its way to fixation or loss. Since the sojourn time of a strongly selected allele is shorter than that of a weakly selected allele, _N_fix and _B_sgv depend on the selection coefficient of the allele. For logistic growth, Equation 19 in Otto and Whitlock (1997) leads to

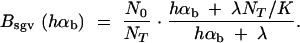	15

Figure 4 shows the percentage of fixations from the standing variation for a bottleneck with NT = N_0/_100 and logistic recovery with ∼5% initial growth per generation and carrying capacity K = 2546. More precisely, we choose λ = 0.05092 · 2_N_0 = 2546 for the growth rate per 2_N_0 = 50,000 generations, such that the average size after the environmental change until 0.1_N_0 generations (i.e., G = 0.05) is _N_av = N_0/_10 = 2500.

Figure 4.—

The probability that an adaptive substitution stems from the standing genetic variation Prsgv in a population with a bottleneck at the time of the environmental change. Dashed lines show a simple reduction in population size by a factor 100 without recovery. Simulation circles and solid lines are for the opposite case of strong logistic recovery (for parameters see main text). The lines follow from the simple analytical approximation Equation 14 with the bottleneck correction R_α → R_α/B_sgv and αb → αb/B_new in the term proportional to G. Direct numerical integration of Equations 5 and 6 with the same bottleneck correction produces a slightly better fit.

From Equation 15 and Figure 4, we can distinguish three parameter regions for the effect of a bottleneck. First, for _h_αb > λ, the fixation probability of individual alleles is not substantially increased by population growth as compared to the case without recovery. However, population growth increases the opportunity for new mutations and thus _B_new < B_sgv. For large Θ_u, there is nevertheless almost no change in Prsgv relative to no recovery. The reason is that fixation is then almost certain, with P_new ≈ 1 and thus Prsgv ≈ P_sgv (see the definition of Prsgv above Equation 14). Second, for very small selection coefficients, h_αb < λ_NT/K, all alleles feel the new carrying capacity K as their fixation effective population size. If λ ≫ 1/G, the bottleneck then acts like a single change in the population size from _N_0 to K. Finally, for intermediate selection coefficients, _P_new generally profits more from the recovery than _P_sgv, leading to a reduction in Prsgv if compared to no recovery.

Compared with the results of the previous section, we can summarize the effect of a bottleneck as follows. There is a tendency to further increase the predominance of the standing variation for weakly selected alleles and to decrease its advantage for high h_αb and Θ_u. However, unless the bottleneck is very strong, there is no qualitative change in the overall pattern.

Footprints of soft sweeps:

Since adaptations from the standing genetic variation start out with a higher copy number of the selected allele, more than one of these copies may escape stochastic loss and eventually contribute to fixation. Depending on whether one or multiple copies are involved in the substitution, one may expect differences in the footprint of the adaptation on linked neutral variation. To derive the probability that n copies of the allele A that segregate in the population at time T contribute to its fixation, we follow Orr and Betancourt (2001) and assume that individual copies enjoy an independent probability to escape stochastic loss. We may then apply a Poisson approximation. If the frequency of A at the time of the environmental change is x, the probability that k = n copies survive and contribute to fixation is approximately

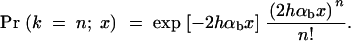	16

This approximation is consistent with Equation 3 if 2_h_αb ≫ 1. The probability that more than one copy contributes to the substitution (i.e., the probability for a “soft sweep”) is then Pr(k > 1; x) = 1 − (1 + 2_h_αb_x_)exp[−2_h_αb_x_]. Averaging over the allele frequency distribution at time T, ρ(x), and conditioning on the case that fixation did occur, we obtain the probability for a soft sweep for adaptations from the standing genetic variation,

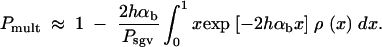	17

Using the approximation Equations 5 and 6 for the allele distribution and Equation 8 for _P_sgv, this gives

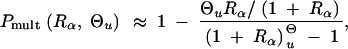	18

which reduces to P_mult ≈ 1 − R_α/((1 + R_α)ln[1 + R_α]) in the limit Θ_u → 0. This limit is essentially reached for Θ_u ≲ 0.004. We can again compare the stochastic result with the deterministic approximation that is obtained from Equation 17 assuming x ≡ Θ_u/_2_h_′αd,

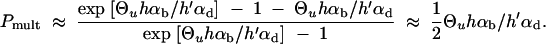	19

Both approximations, Equations 18 and 19, are compared to simulation data in Figure 5. The deterministic approximation reproduces the stochastic result only for very large mutation rates, Θ_u_ ≫ 1, outside the parameter space in the figure. For low mutation rates, where Equation 19 predicts a zero limit for Θ_u_ → 0 it severely underestimates _P_mult. The stochastic approximation produces a reasonable fit unless _h_′αd and _h_αb are both small. In this parameter range with relatively high initial allele frequency and weak positive selection, the Poisson approximation is no longer valid.

Figure 5.—

The probability that multiple copies from the standing genetic variation contribute to a substitution, _P_mult. Solid lines correspond to Equation 18 and dotted lines to the deterministic approximation Equation 19.

To estimate the impact of a soft sweep on linked neutral variation we are also interested in the number of independent copies that contribute to the fixation of the allele, i.e., copies that are not identical by descent. Concentrating on copies that segregate in the population at the time T of the environmental change, we can again use a Poisson approximation, P̃r(k = n) = exp(−λ)λ_n/n_!. With this conjecture, 1 − exp(−λ) is the fixation probability from the standing genetic variation. Equating with P_sgv as given in Equation 8, we obtain λ = Θ_u ln[1 + _R_α]. The probability of fixation of multiple independent copies, conditioned on the cases where fixation occurs then is

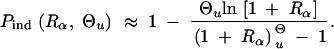	20

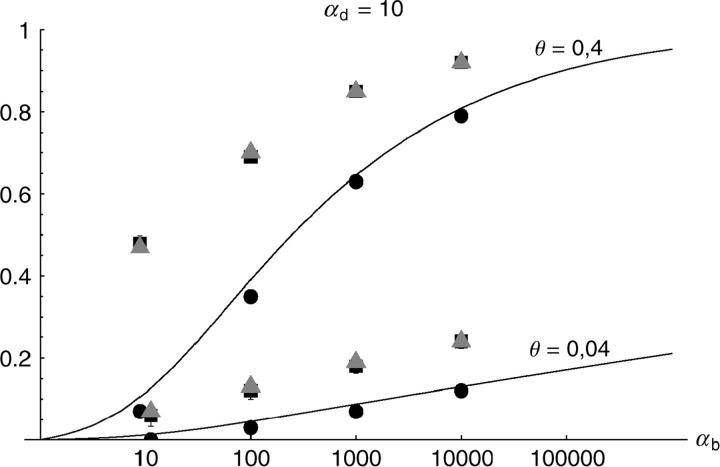
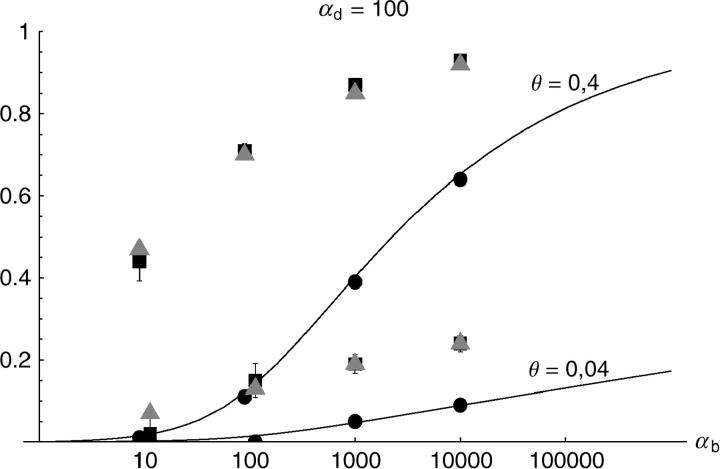
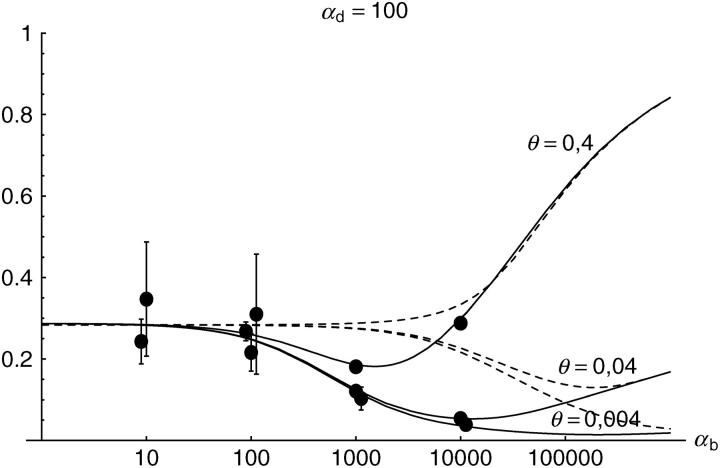
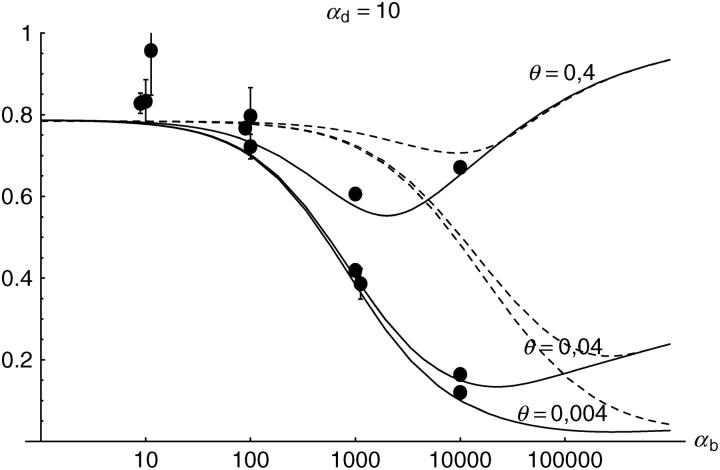
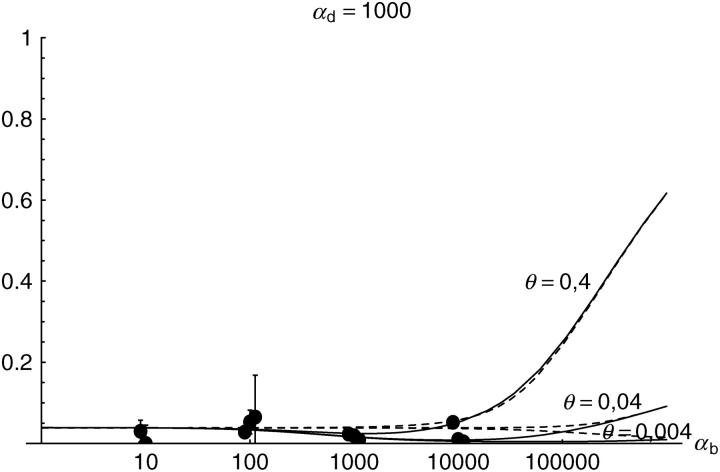
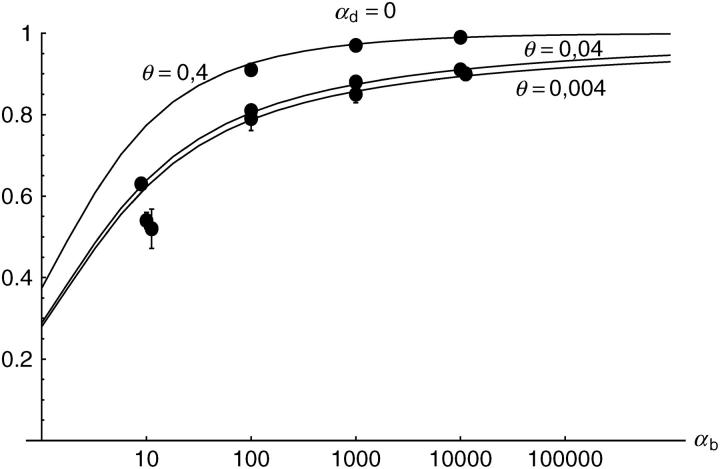
Alternatively, we obtain Equation 20 from Equation 18 using the relation 1 − P_mult(Θ_u) = (1 − P_ind(Θ_u))(1 − P_mult(Θ_u = 0)). This equation expresses the probability for fixation of a single copy (“no multiple fixation given fixation”) as the probability of fixation from a single origin times the probability of fixation of a single copy given that all successful copies are from a single origin (a single origin is enforced in P_mult by Θ_u → 0). This alternative derivation shows that Equations 18 and 20 follow from the same assumption: independent fixation probability for different copies. To the order of our approximation, _P_mult and P_ind depend on selection only through the relative selective advantage R_α = 2_hs_b/(2_h_′_s_d + 1/(2_N_e)). This parameter combines two effects. The denominator of _R_α takes into account that multiple fixations are less likely if the initial frequency of the allele at time T is low. This frequency decreases with deleterious selection _h_′_s_d and drift, represented by the 1/2_N_e term. Second, the numerator of _R_α accounts for the fixation probability of the allele: The probability that the allele is maintained during the adaptive phase increases with _hs_b. For _h_αd ≫ 1, the result depends only on the ratio of the selection coefficients as also predicted by the deterministic approximation (Orr and Betancourt 2001). If the environmental change is followed by a bottleneck, Equations 18 and 20 can be used with R_α → R_α/B_sgv with the bottleneck factor introduced above. In contrast to P_mult, the fixation probability of multiple independent copies depends strongly on the mutation rate Θ_u and vanishes for Θ_u → 0. In Figure 6, Equation 20 is compared with simulation data. The approximation produces a good fit for αd ≥ 10 where the Poisson approximation is valid.

By construction, both approximations (18) and (20) account only for the fixation of copies of the allele that were already in the population at time T. It is, however, also possible that a successful copy first arises for t > T as a new mutation during the adaptive phase. Since the origin of these new copies is necessarily independent, this effect contributes to P_ind. The size of this contribution depends on the population-level mutation rate Θ_u,t_>T directly after the environmental change. Θ_u,t_>T can be smaller than the original Θ_u that appears in Equations 18 and 20 if there is a bottleneck at T. For Θ_u_,t_>T = Θ_u our simulation results show that the contribution of new mutations to _P_ind is substantial (Figure 6, squares). One consequence of mutational input after T is that _P_ind becomes almost independent of αd. Even more importantly, we see that the fixation of multiple independent copies is not particular to adaptations from the standing genetic variation. It occurs with basically the same probability if the selected allele enters the population after the environmental change as a recurrent new mutation (see Figure 6, triangles).

For recurrent new mutations, the simulation data show that the total fixation rate of multiple independent copies, _r_ind = −ln[1 − P_ind], increases logarithmically with αb and linearly with Θ_u. For a heuristic understanding of this dependence, assume h = 0.5 and let x(t) be the frequency of a first copy of the selected allele on its way to fixation in the absence of further mutation. For small u, the probability for a second copy of the beneficial mutation to arise while a first copy spreads to fixation is then 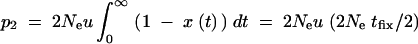. Here, _t_fix is the average fixation time in 2_N_e generations and we have used that the first copy spends on average equal times in frequency classes x and (1 − x). By far the largest contribution to _p_2 comes from the early phase of the sweep where the frequency x of the first copy is very low. The probability of the second copy to survive until fixation of the allele depends on x, but to leading order only the survival probability for x → 0 matters, which is approximately _s_b. With _t_fix from Equation A17 we then obtain 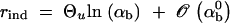. A more detailed account will be given elsewhere.

_P_ind is the probability that descendants of multiple independent copies of the selected allele segregate in the population at the time when this allele reaches fixation. Consequently, the number of copies in our simulation runs was counted at the time of fixation (same for _P_mult). In practical applications, however, one is often interested in the probability of observing descendants from independent origins a fixed time G after an environmental change. This probability will decrease with G, since copies get lost by drift until, eventually (in the absence of back mutation), all copies derive from a single mutation as their common ancestor. The drift phase from the time of fixation to the time of observation G depends on the selection coefficient and will be longer for strongly selected alleles with short fixation times. In principle, this could affect the dependence of the probability of observing multiple fixed copies in a population on _h_αb. To test this, we ran additional simulations to measure the probability for the survival of multiple (independent) copies G = 0.1_N_e generations after the environmental change (results not shown). For alleles with fixation time _t_fix < 0.1_N_e, we did not detect any difference from the data displayed in Figures 5 and 6, meaning that fixation of a single copy in the neutral drift phase after initial fixation of multiple copies is rare. This is not surprising, considering that the average fixation time under neutral drift exceeds 0.1_N_e generations even if the frequency of the major copy is initially at 99%.

Another question is whether multiple copies of the selected allele are likely to be found in a small experimental sample, even if they exist in the population. We tested this by arbitrarily drawing 12 chromosomes in each case of a soft sweep. Multiple copies in the sample were found in 70–80% of all cases (for Θ_u_ = 0.4). Summarizing our results for the fixation probabilities of multiple copies and of multiple independent copies, we can distinguish three parameter regions:

• Low mutation rate, relatively strong past selection: If the mutation rate is low (Θ_u_ ≪ 0.1) fixation of multiple independent copies of the selected allele is unlikely. If multiple copies fix, they are most likely identical by descent. If past deleterious selection is strong, however, also the fixation of multiple homologous copies is rare. For Θ_u_ = 0, Equation 18 indicates that <5% and <30% of fixations originate from multiple copies for _R_α ≤ 0.1 and _R_α = 1, respectively (Figure 5).
• Low mutation rate, relatively weak past selection: With increasing relative advantage R_α the fixation of multiple homologous copies increases. For Θ_u → 0, fixation of multiple copies occurs in >50% of the cases (_P_mult > 0.5) if _R_α ≳ 4 (Figure 5).
• High mutation rate: For mutation rates Θ_u_ ≳ 0.1 fixations from independent origins are much more frequent and become more likely than the fixation of single copies. This holds true for whether the origin of the selected allele is from the standing variation or from recurrent new mutations. The fixation probability for multiple independent copies increases logarithmically with h_αb. For Θ_u = 0.4, 50–90% of substitutions involve multiple independent copies (Figure 6).

Imagine that we observe a DNA region where an adaptive substitution has happened following an environmental change at time T. Suppose that we observe this region G generations after the environmental change, and 2 ≫ G ≫ _t_fix, such that the advantageous allele has reached fixation, but G (in units of 2_N_e) is much shorter than the average neutral coalescent time. We want to analyze whether and how the contribution of multiple copies to an adaptive substitution affects the signature of selection on linked neutral variation. For this, it is helpful to distinguish two aspects of a selective footprint, its width in base pairs along the sequence and its maximum depth in terms of the extent of variation lost in a region close to the locus of selection.

For a hard sweep, the coalescent at the selected site itself does not extend beyond time T. Ancestral variation that has existed prior to T can be maintained only if there is recombination between the selected site and the site studied. In a core region around the selected site, where no recombination has happened, all ancestral variation is lost. Recombination therefore modulates the width of the sweep region, but in general does not affect its maximum depth. Since only recombination in the selective phase matters, and since the adaptive phase is much shorter for a strongly selected allele, the width of a selective footprint decreases with larger αb.

For a soft sweep, the coalescent at the selected site itself extends into the ancestral environment. As compared with a hard sweep, a soft sweep therefore has a reduced maximum depth. Our results show that soft sweeps with shallower footprints are more likely for large αb. This does not contradict that selective footprints get weaker and eventually vanish as αb → 0, for two reasons. First, even if it is more likely for lower αb that all ancestral variation is eliminated close to the selection center, the width of the window where this holds true gets smaller at the same time. If this width drops below the average distance of polymorphic sites, the footprint of selection becomes undetectable. Second, if we observe the sweep region G generations after positive selection begins, we can compare only selective footprints of alleles that have reached fixation by this time. If we want to study very weakly selected alleles, G needs to be so large that any footprint of selection will be washed out by new mutations that arise after time T.

The impact of a soft sweep on the molecular signature depends on whether the surviving copies are independent by descent or not. Copies from different origins are related by a neutral coalescent and represent independent ancestral haplotypes. If these haplotypes are sampled close to the locus of selection, this should mark a clearly visible difference from the classic pattern of a hard sweep. A detailed quantitative analysis with estimates of the impact on summary statistics for nucleotide variability exceeds the aims of this study and will be given elsewhere.

If multiple surviving copies are identical by descent, the expected change in the molecular footprint relative to a hard sweep depends on the strength of deleterious selection that the allele has experienced prior to the environmental change. We expect a shallower footprint (and larger deviation from the hard sweep) for weaker deleterious selection. The reason is that it is more likely for a weakly deleterious allele to segregate in a population for a long time; i.e., the average time to the most recent common ancestor in the core region of the sweep is larger for smaller αd. Indeed, this intuition can be made more precise.

A remarkable property of the Markov process that underlies the Wright-Fisher model is that, conditional on an allele A having reached some frequency x in a population, this process is independent of the sign of the selection coefficient of A (cf. Ewens 2004, Chaps. 4.6 and 5.4; for simplicity, we assume Θ_u_ = 0 and h = _h_′ = 0.5). This has interesting consequences for adaptations from mutation-selection-drift balance. Assume that an allele A with selective disadvantage _s_d that is derived from a single mutation segregates in the population at frequency x at the time T of the environmental change. Then the mean age of this allele and, more generally, the average time that it spent in each frequency class in the past are the same as if it had a selective advantage of the same absolute size prior to T. Assume that A spreads to fixation under positive selection with selection coefficient _s_b after the environmental change and compare this with a sweep of an (imaginary) allele _A_′ with the same frequency x at time T, but selective advantage _s_b throughout. For _s_d = _s_b, the total fixation time of the alleles and their sojourn times in every frequency class are the same; for _s_d < _s_b (resp. _s_d > _s_b) they are longer (shorter) for A.

The above argument shows that the footprint of a sweep from the standing genetic variation is identical to a “usual” sweep pattern if the selection coefficient changes its sign, but not its absolute value upon the environmental change. If we observe the sweep region at time G, the only difference from a sweep that has originated from a new mutation after time T is the somewhat older age of the sweep from the standing variation. For _s_d ≠ _s_b, the change in the selection regime leads to differences in the expected footprint of alleles A and _A_′. Clearly, this difference is due to the cases where the coalescent of A (and _A_′) extends into the old environment, i.e., where the sweep is “soft.” For _s_d > _s_b, the expected coalescence in the ancestral environment is faster for A than for _A_′, leading to a stronger footprint of selection. However, since soft sweeps are very rare for _s_d > _s_b, this will hardly lead to a detectable difference in the average footprint.

Let us now concentrate on the case _s_b > _s_d, or _R_α > 1, where soft sweeps are frequent. In this case, the coalescence in the ancestral environment is slower and the selective signature for A is reduced in depth and width relative to _A_′ (due to the increased opportunity for mutation and recombination until the allele is fully coalesced). If the frequency x of the allele at time T is large, the sweep pattern of A will look more like a sweep of an advantageous allele with a selection coefficient of size _s_d < _s_b. We therefore also expect to find a larger difference between the footprints of soft sweeps and hard sweeps from a new mutation in this case. For a rough estimate of when this difference should be detectable, we compare the total fixation times of the allele A in the case of a soft sweep, _t_fix,soft(_s_d, _s_b), with the average duration of a sweep from a new mutation _t_fix(_s_b) (cf. Equation 13). For an optimal (that is, minimal) time of observation G ≈ _t_fix(_s_b), we expect a clear difference in the selective signatures if the increase in coalescence time is of the same order of magnitude as the original coalescence time. Estimating the relative change in coalescence time by the change in fixation time, this means _t_Δ = _t_fix,soft(_s_d, _s_b) − _t_fix(_s_b) ≳ _t_fix(_s_b). We derive _t_Δ from the frequency distribution of the allele at the time T conditional on multiple fixation and results from diffusion theory on the expected age of an allele given its frequency; details are given in the appendix. The results (not shown) predict visible changes in the sweep pattern for a minimum of _R_α between 20 and 100.

DISCUSSION

The adaptive process is the genetic response of a population to external challenges. In nature, these challenges may be due to changes in climate or food resources or arise with the advent of a new predator or parasite. They either affect the original habitat of the population or are a consequence of the colonization of a new niche or of human artificial selection. In this article, we are interested in the adaptive response of a previously well-adapted population to a sudden and permanent change. We concentrate on a single locus with two (classes of) alleles, one, a, ancestral, and the other, A, derived. Allele A is either neutral or deleterious under the original conditions, but selectively advantageous after the change in the selection regime at some time T. We compare two scenarios: either A already segregates in the population at time T and fixes from the standing genetic variation or the population adapts from a new copy of the allele that enters the population only after the environmental shift.

Our results rely on two main assumptions. First, and most importantly, we assume that adaptation of the target allele does not interfere with positive or negative selection on other alleles, through either linkage or epistasis. This assumption is usually made in population genetic studies of selective sweeps. It is satisfied if the rate of selective substitutions is low and the time to fixation for each individual substitution is short, but is less plausible for weakly selected alleles with long average fixation times. In general, interference reduces fixation probabilities, with a stronger influence on weak substitutions (Barton 1995), although this does not translate into a large effect on the reduction of heterozygosity due to a selective sweep (Kim and Stephan 2003). In their study of fixation probabilities of alleles from the standing variation, Orr and Betancourt (2001) did not find a large effect of interference. This, however, may be a consequence of the neglect of new mutations and the restriction to a low initial frequency of the selected allele in their simulations. These assumptions make it unlikely that two or more beneficial alleles escape early stochastic loss and compete on their way to fixation. We therefore emphasize that our results are conditional on noninterference. Second, we assume that the variation at the locus under consideration is maintained in mutation-selection-drift balance prior to the environmental change. If selected alleles are maintained as a balanced polymorphism or are not in equilibrium at all, this may clearly affect our conclusions.

Our results pertain to three main issues: the dependence of fixation probabilities on selection coefficients if alleles are taken from the standing genetic variation, the relative importance of the standing variation and new mutations as the origin of adaptive substitutions, and the expected impact of a selective sweep from the standing genetic variation on linked nucleotide variation. We discuss them in turn.

Fixation probability from the standing variation:

In a famous argument that helped to found the micro-mutationist view of the adaptive process, Fisher (1930) showed that mutations with a small effect are much more likely to be beneficial than mutations with a large effect. Kimura (1983), however, pointed out a flaw in this argument: Even if a large majority of new beneficial mutations has a small effect, as Fisher argues, this may be offset by a much smaller fixation probability of weakly selected alleles. An allele with (constant) heterozygote advantage _hs_b that enters the population as a single new copy will escape stochastic loss and spread to fixation with probability 2_hs_b. One can think of stochastic loss as a sieve where small-effect alleles pass through the holes—and vanish from the population—much more often than alleles with a large selective advantage. A variant of this picture is known as Haldane's sieve and pertains to different levels of dominance: Substitutions are likely to be dominant since dominant alleles enjoy higher fixation rates.

This latter scenario is the subject of Orr and Betancourt (2001), who study Haldane's sieve if selected alleles are taken from the standing genetic variation. They conclude that the sieve is not active in this case. If the selected allele is deleterious under the original conditions (with heterozygote disadvantage _h_′_s_d), and if the level of dominance is maintained upon the environmental shift, h = h_′, the net fixation probability is approximately independent of dominance. It is easy to understand why: The advantage of a higher fixation rate with larger h is compensated by the lower frequency of the initially deleterious allele in mutation-selection balance. Orr and Betancourt (2001) focus on a limited parameter range, where the selected allele is definitely deleterious under the original conditions and thus starts at a low frequency. In their calculations, they also assume that the original deleterious effect is larger than the subsequent beneficial effect of the allele, meaning that the relative selective advantage R_α = 2_h_αb/(2_h_′αd + 1) < 1. Our study extends their analysis to arbitrary values of _R_α. The simple analytical approximation for the probability of a substitution from the standing variation (Equation 10 above, resp. Equation 3 in Orr and Betancourt 2001), which uses the deterministic value for the initial frequency of A in mutation-selection balance, is no longer valid in the general case. Nevertheless, there is an equally simple expression, Equation 8, which serves as an approximation for the entire parameter range.

Our results corroborate and extend the findings of Orr and Betancourt (2001). To the order of our approximation, the fixation probability from the standing genetic variation depends on selection only through _R_α. If selection is strong in both environments, and _h_′ = h, it is independent of dominance. More generally, if beneficial and deleterious effects of alleles in different environments were strictly proportional, the distribution of the effects of adaptations from the standing variation would coincide with the distribution of the effects of new beneficial mutations, as implicitly assumed in Fisher's (1930) argument. The reason is the same as in the case of dominance: Advantages in the fixation probability due to a larger αb are compensated by disadvantages due to a smaller initial frequency with higher αd.

Remarkably, we find that the stochastic sieve is substantially weakened even if alleles with a larger selective advantage do not have a larger disadvantage to compensate for it. If alleles are originally neutral or under relatively weak deleterious selection, such that _R_α > 1, there is only a very weak logarithmic dependence of the fixation probability on all parameters for selection or dominance. The reason is the high initial frequency of the successful alleles in this case, which may be much higher than the average frequency of all segregating alleles. At these high frequencies, the fixation probability is only weakly dependent on the selection coefficient of the allele. There is, however, a sieve acting against alleles under disproportionately large past selection, _R_α < 1. If the selected physiological function (with fixed _h_αb) is met by several alleles with different _h_′αd, alleles with a relatively mild deleterious effect in the past, _h_′αd < _h_αb, will be preferred. Note that this should confer a certain level of resilience to the population if the environmental conditions change back.

Empirical estimates of _R_α, the relative selection strength, are difficult to obtain and generally not available. There is no a priori reason to assume that _s_b is either larger or smaller than _s_d (_s_b < _s_d was assumed by Orr and Betancourt 2001). To see this, note that the roles of the alleles _A_ and _a_ and the selection coefficients _s_b and _s_d are exchanged if the environment changes back to the old conditions at some later time. This argument does not pertain to the average selection coefficient of _any_ deleterious allele (which is plausibly larger than the average beneficial effect), but only to the selection coefficients of deleterious alleles that are beneficial in the new environment. Several factors can cause an upward or downward bias of _R_α. _R_α is downward biased if there is a bottleneck at the time of the environmental change. In this case, the effective population size that enters αb is reduced relative to the original _N_e that enters αd. An upward bias in _R_α could result from a change in dominance following the environmental shift. To see this, assume that alleles _a_ and _A_ serve different functions that are only (or mostly) used in the old and new environments, respectively. The physiological theory of dominance claims that the common observation of dominant wild-type alleles is a natural consequence of multienzyme biochemistry (_e.g._, Kacser and Burns 1981; Orr 1991; Keightley 1996). If this holds true, it is natural to expect that there is at least partial dominance of the respective advantageous (wild-type) allele, hence of _a_ (_A_) in the old (new) environment, and thus _h_ > _h_′. Finally, if _R_α is measured among successful substitutions from the standing genetic variation, a further upward bias results from the stochastic sieve against alleles with large _h_′αd.

Relative importance of adaptations from the standing variation and from new mutations:

To estimate the importance of the standing genetic variation as a reservoir for adaptations, we compare a polymorphic population, in mutation-selection-drift balance, with a monomorphic one. We can measure the additional adaptive potential of the polymorphic population in the number of generations _G_sgv that a monomorphic population must wait for sufficiently many new mutations to arrive to match the fixation probability from the standing variation. G_sgv can be very large for mutations with small effect (of the order 1/hs_b generations). However, for a population of constant size it is always smaller than the average fixation time of the allele. This means that there is no clear separation of adaptive phases: By the time most alleles from the standing genetic variation with a given selective advantage _h_αb have reached fixation, substitutions from new mutations (with the same _h_αb) will also be found. Only if the environmental change is followed by a strong reduction in population size is the reservoir of the standing variation exploited well before new mutations start to play a role.

We have also determined the probability that the standing variation contributes to an adaptive substitution that is observed some time G after an environmental change. Clearly, this probability generally declines with G. For fixed G there are two distinct parameter regions where the standing variation is most important.

1. Adaptations from the standing variation are favored for alleles with small effect that are under relatively weak past selection, R_α ≥ 1. This is a direct consequence of the stochastic sieve that eliminates weak alleles in a new mutation scenario. The effect is especially pronounced if the environmental shift is followed by a bottleneck with incomplete recovery. The percentage of substitutions that use alleles from the standing variation is then almost independent of the mutation rate since Θ_u affects the fixation probabilities from standing and new variation in the same way.
2. The standing variation is also important for alleles with a large relative selective advantage (R_α ≫ 1) if the mutation rate Θ_u is also high. In this case, fixation probabilities are high under both scenarios, new mutations and standing genetic variation. Since the standing variation other then new mutations is immediately available, it will usually contribute a major share to the substitution. Note that R_α ≫ 1 is plausible in particular for “important” adaptations with large effect, such as insecticide-resistance alleles. Whether such an adaptation likely originated from the standing genetic variation then depends mainly on Θ_u.

Selective footprints of soft sweeps:

For a classical sweep from a single new mutation, which we call a hard sweep, ancestral variation can be preserved only if there is recombination between the polymorphic locus and the selection target during the selective phase. In a “core” region around the selection center all ancestral variation is erased. In contrast, with a soft sweep, multiple copies of the selected allele contribute to the substitution. Depending on the history of these copies, part of the ancestral variation may then be maintained and appear as haplotype structure in the population. There are two types of soft sweeps. For the first type, multiple copies that contribute to the substitution derive from independent mutations. For the second type, multiple copies that existed at the time of the environmental change contribute to the substitutions, but these copies are identical by descent.

Soft sweeps of the first type (independent origins) are frequent if the mutation rate on the population level is sufficiently high (Θ_u_ ≳ 0.1); see Figure 6. Their probability relative to a sweep from a single origin also increases with the selection strength _h_αb, i.e., altogether for alleles with high adaptive rates. Suprisingly, soft sweeps of this type are not exclusive to adaptations from the standing genetic variation, but occur with the same probability for adaptations that originate only from new mutations, which have entered the population after the environmental change. Even if material from the standing variation is used, most soft sweeps with copies from independent origins also involve new mutations. Since surviving copies represent independent ancestral haplotypes, we expect characteristic differences in the selective footprint relative to the classic pattern of a hard sweep, where only a single ancestral haplotype survives in the core region close to the selection site. A discussion of the effect of soft sweeps on the summary statistics for nucleotide variation will be given elsewhere.

Soft sweeps of the second type (copies with a common origin prior to the environmental change) can occur only for adaptations from the standing genetic variation. They are frequent even for a very low mutation rate Θ_u_ → 0 if the allele has a high relative selective advantage _R_α ≳ 4; see Figure 5. The sweep pattern depends on the strength of deleterious selection that the allele has experienced in the old environment. For _R_α > 1, we expect a weaker footprint with a narrower sweep region than predicted for a hard sweep with the same selective advantage _h_αb. We predict, however, that differences in the sweep patterns are visible only for a minimum _R_α of 20–100. For αd = 0, where the probability of multiple fixations and the resulting effect on the sweep pattern are strongest, this has been studied in a recent publication by Innan and Kim (2004). Using computer simulations, these authors indeed find much weaker selective footprints if the alleles are taken from the standing genetic variation. Since their minimum value of _R_α is 1000, their results fit our predictions.

We can summarize our results on soft sweeps in three observations. First, evidence of a soft sweep does not result in an easy criterion to distinguish adaptive substitutions from the standing variation and recurrent new mutations. For a large parameter space we will not be able to detect any difference between these adaptive scenarios. This confirms the conclusion of Orr and Betancourt (2001), although partly for different reasons. For high Θ_u_ ≳ 0.1, soft sweeps are frequent in both cases; for low Θ_u_ and _R_α ≲ 20 they either are rare in both cases or do not lead to significant differences in the selective footprints. For a range of “interesting” substitutions, namely alleles with a large effect but a low mutation rate, however, the linked nucleotide pattern could be informative.

Second, soft sweeps are frequent in a limited but relevant parameter space. We expect soft sweeps with characteristic patterns on the selective footprints for high Θ_u_, i.e., either if the population size is large or if the allelic mutation rate is high, such as at mutational hotspots or if the adaptation corresponds to a loss-of-function mutation of the gene. We also expect soft sweeps for large adaptations with _h_αb ≫ _h_′αd (thus _R_α ≫ 1) from the standing variation, even if the mutation rate is small. The effect of a soft sweep in this last case is a reduction in the width of the sweep region relative to a hard sweep. A possible candidate for a soft sweep of this type is the evolution of DDT resistance in non-African populations of D. melanogaster. In recent studies of nucleotide and microsatellite variability in the region around an Accord insertion that is associated with DDT resistance, Schlenke and Begun (2004) and Catania et al. (2004) found evidence for a selective sweep. The width of the sweep region, however, was much narrower in D. melanogaster than expected under putatively very strong selection (Catania et al. 2004) and, as observed, for the “same” adaptation (with a Doc insertion) in D. simulans (Schlenke and Begun 2004).

Third, while hard sweeps from single mutations produce the strongest footprint for strongly selected alleles with short fixation times, the possibility of fixation of multiple alleles leads to an opposite trend: Soft sweeps with weaker footprints are more frequent for high αb. Since the increase is only logarithmic, this trend is not very strong. Nevertheless, it could be visible for nucleotides that are tightly linked to the selected allele in regions of low recombination or in sufficiently small windows around the selection target. A genome-wide study of the small-scale reduction of heterozygosity in narrow windows of 200 bp around replacement or silent fixations has recently been performed for D. simulans by Kern et al. (2002). We note that their counterintuitive finding of a sweep signature for preferred codon substitutions, but not for replacement substitutions, matches our prediction of a stronger sweep signal for weakly selected alleles close to the selection center. However, a quantitative analysis of soft sweeps that also accounts for other factors like population substructure is needed before any conclusions can be drawn.

Acknowledgments

We thank Sylvain Mousset and Wolfgang Stephan for fruitful discussions and John Parsch for helpful comments on the manuscript. The careful comments by Sally Otto and an anonymous reviewer led to many clarifying changes. We also thank Pieter van Beek for help with the computer simulations. This work was supported by an Emmy Noether grant from the Deutsche Forschungsgemeinschaft to J.H.

APPENDIX

Fixation probability for a mutation segregating at neutrality:

We calculate the average fixation probability of an allele that is derived from a single mutation and segregates in the population under neutrality at the time T of the environmental change. The probability that there are exactly k copies at time T is distributed as ρ(k) = _aNk_−1, where 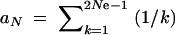. Assuming a selection coefficient _s_b for t > T and no dominance (h = 0.5), the average fixation probability is given by

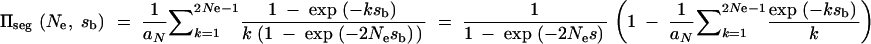	A1

We derive the sum in (A1) as

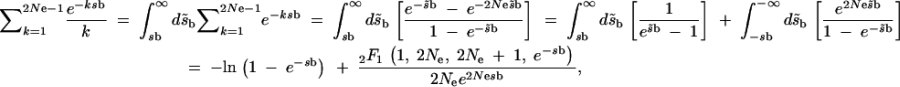	A2

where 2_F_1 denotes the hypergeometric function. For _N_e_s_b ≫ 1, this second term can be neglected and we obtain

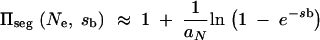	A3

In the limit of small _s_b and large _N_e this reduces to

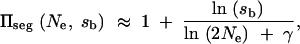	A4

where γ = 0.577 … is Euler's constant. For weak recessivity, this result holds if we replace _s_b by 2_hs_b.

Fixation probability for allele in mutation-selection-drift balance:

To calculate the frequency distribution of a derived allele, we start out with the Kolmogorov forward equation that describes the Wright-Fisher model in the diffusion limit (Ewens 2004),

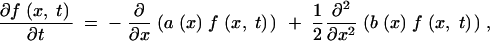	A5

where

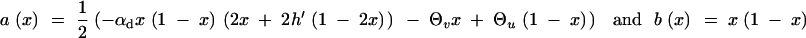	A6

are the drift and diffusion terms. Forward mutations are measured by Θ_u_; back mutations are measured by Θ_v_. Since the diffusion process is ergodic, the probability that the frequency of an allele falls into a certain interval [_x_1, _x_2] is proportional to the average time T that an allele that starts out as a single copy spends in this frequency range before it is either lost or fixed. The frequency distribution therefore directly follows from the well-known transient behavior of the process, e.g., Ewens (2004)(Chap. 4). From Equations 4.23 and 4.16 in Ewens (2004), we obtain

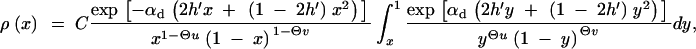	A7

where C is a normalization constant. Note that this expression deviates from Wright's stationary distribution of an allele in mutation-selection-drift balance since we condition on the case that A is derived.

Simple approximate relations for Equation A7 are readily obtained in various limiting cases. First, direct numerical integration shows that back mutations can safely be ignored even in the neutral case αd = 0 because most alleles segregate at low frequencies (this is a consequence of conditioning on derived alleles). In the neutral case, this approximation directly leads to Equation 5. If there is deleterious selection, we need to distinguish cases of weak and strong recessivity of the allele A. We concentrate mostly on the case where deleterious selection on the heterozygote is sufficiently strong, 2_h_′αd ≫ (1 − 2_h_′)/2_h_′ (i.e., weak recessivity). Under these conditions, we can ignore the quadratic terms in the exponentials and express ρ(x) in terms of incomplete Gamma functions,

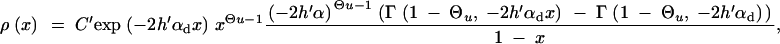	A8

with normalization constant _C_′. For definitely deleterious A (2_h_′αd ≥ 10 is sufficient), the integrand in Equation A7 is concentrated near y = 1. We can then expand y_Θ_u in the denominator to leading order around y = 1 (i.e., y_Θ_u ≈ 1) and obtain ρ(x) in terms of simple functions, which leads to Equation 6.

To obtain an analytical expression for the probability of fixation P_sgv or multiple fixation P_mult, we need to approximate ρ(x) further. If the allele A is neutral prior to the environmental change, and Θ_u ≪ 1, ρ_x in Equation 5 is ∼ρ_x_ ≈ Θ_u_ _x_Θ_u_−1. Using this in Equation 4,

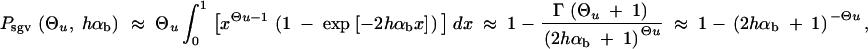	A9

where we extend the integral over exp(−2_h_αb_x_) to ∞ after increasing 2_h_αb by 1 to avoid a singularity near αb = 0. We also use Γ(Θ_u_ + 1) ≈ 1 for 0 ≤ Θ_u_ ≤ 1.

For the deleterious case (2_h_′αd ≫ 1), note that the allele frequency distribution is significantly larger than zero only for x ≤ 1/2_h_′αd. Expanding around x = 0 we can approximate ρ(x) in Equation 6 as ρ_x_ ≈ C_″_x_Θ_u_−1exp−2_h_′αd_x and obtain

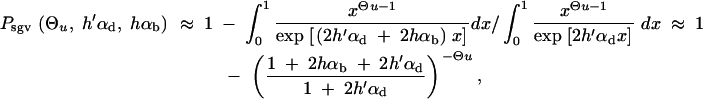	A10

which gives Equation 8. In Equation A10, we have again extended integral limits after adding 1 to 2_h_′αd, respectively 2_h_αb + 2_h_′αd. We now see that the approximation for 2_h_′αd ≫ 1 reproduces the approximation for αd = 0 in the limit αd → 0. We can therefore use it in the entire parameter range. For Θ_u_ < 1, the probability that the allele A is not contained in the standing variation at time T can be approximated by the integral over ρ(x) from 0 to 1/2_N_e (confirmed by simulations; see also Ewens 2004, Chap. 5.7). With the above approximations for ρ(x) this results in Equation 7. Finally, also _P_mult is obtained by an analogous calculation.

If the allele A is completely recessive prior to the environmental change, _h_′ = 0, we again obtain an expression in incomplete Gamma functions for ρ(x) similar to Equation A8. For large αd, this reduces to

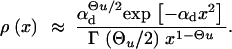	A11

Using this expression in Equation 4, we see that the term exp[−αd_x_2] can be ignored as long as 2_h_αb > 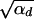since the integral is cut off by exp[−2_h_αb_x_]. For 2_h_αb < 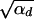, both selection coefficients are important. We can obtain a simple, yet compared to simulation data (not shown) reasonable, analytic approximation that captures this crossover behavior by formally replacing 2_h_′αd + 1 by 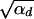+ 1 in Equations 8, 7, and 18 if _h_′ = 0.

The average frequency of the allele A at time T conditioned on later fixation, 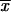fix, is calculated from the distribution Pr(x|fix) = C_ρ(x)Π_x(_h_αb). With the above approximations for ρ(x), we obtain

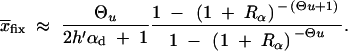	A12

For Θ_u_ → 0, this gives

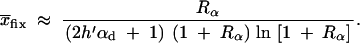	A13

Finally, if also αd = 0 and 2_h_αb ≫ 1,

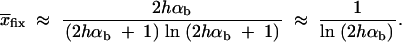	A14

For the calculation of the average increase in the age of a selected allele for a soft sweep with a weak trade-off, we use the frequency distribution of the allele at time T conditioned on multiple fixation, Pr(x|mfix) ≈ C_ρ(x)(Π_x(h_αb))2. [We use the Poisson approximation Equation 16 and 2_h_αb_x ≈ 1 − exp(−2_h_αb_x_) for small x, where ρ(x) is large.] We consider only the case Θ_u_ → 0 and h = _h_′ = 0.5. For a given allele frequency x at time T, we determine the average age ta(αd, x) of the allele using Equation 5.113 in Ewens (2004) (see also Kimura and Ohta 1969),

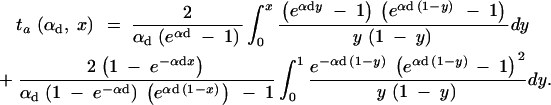	A15

The increase in the age of the allele due to the change of the selection regime then is obtained by numerical integration as _t_Δ = ∫(ta(αd, x) − ta(αb, x))Pr(x|mfix)dx. Choosing x = 1, Equation A15 allows for a simple approximation for the fixation time of a new allele with selective advantage αb. We derive

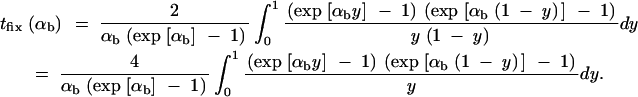	A16

For αb ≥ 3, this may be approximated as

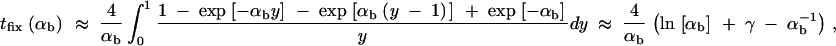	A17

where γ ≈ 0.577 is Euler's Gamma. The error term is of order α−3b. To the best of our knowledge, this simple result has not yet been used in the literature. Simulation results of our own (not included) and in Kimura and Ohta (1969) show that the estimate is very accurate. For h ≠ 0.5, we can replace αb by 2_h_αb in Equation A17. The approximation then holds as a lower bound for _t_fix, since the fixation time increases if h deviates from 0.5 in either direction.

References

1. Barton, N. H., 1995. Linkage and the limits to natural selection. Genetics 140**:** 821–841. [DOI] [PMC free article] [PubMed] [Google Scholar]
2. Barton, N. H., 1998. The effect of hitch-hiking on neutral genealogies. Genet. Res. 72**:** 123–133. [Google Scholar]
3. Catania, F., M. O. Kauer, P. J. Daborn, J. L. Yen, R. H. Ffrench-Constant et al., 2004. World-wide survey of an Accord insertion and its association with DDT resistance in Drosophila melanogaster. Mol. Ecol. 13**:** 2491–2504. [DOI] [PubMed] [Google Scholar]
4. Ewens, W. J., 2004 Mathematical Population Genetics, Ed. 2. Springer, Berlin.
5. Falconer, D. S., and T. F. C. Mackay, 1996 Introduction to Quantitative Genetics. Addison Wesley Longman, Harlow, Essex, UK.
6. Fisher, R. A., 1930 The Genetical Theory of Natural Selection. Oxford University Press, Oxford.
7. Haldane, J. B. S., 1927. A mathematical theory of natural and artificial selection. Part V: selection and mutation. Proc. Camb. Philos. Soc. 23**:** 838–844. [Google Scholar]
8. Hansen, T. F., C. Pelabon, W. S. Armbruster and M. L. Carlson, 2003. Evolvability and genetic constraint in Dalechampia blossoms: components of variance and measures of evolvability. J. Evol. Biol. 16**:** 754–765. [DOI] [PubMed] [Google Scholar]
9. Houle, D., 1992. Comparing evolvability and variability of quantitative traits. Genetics 130**:** 195–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
10. Innan, H., and Y. Kim, 2004. Pattern of polymorphism after strong artificial selection in a domestication event. Proc. Natl. Acad. Sci. USA 101**:** 10667–10672. [DOI] [PMC free article] [PubMed] [Google Scholar]
11. Kacser, H., and J. A. Burns, 1981. The molecular basis of dominance. Genetics 97**:** 6639–6666. [DOI] [PMC free article] [PubMed] [Google Scholar]
12. Kaplan, N. L., R. R. Hudson and C. H. Langley, 1989. The “hitchhiking effect” revisited. Genetics 123**:** 887–899. [DOI] [PMC free article] [PubMed] [Google Scholar]
13. Keightley, P. D., 1996. A metabolic basis for dominance and recessivity. Genetics 143**:** 621–625. [DOI] [PMC free article] [PubMed] [Google Scholar]
14. Kern, A. D., C. D. Jones and D. J. Begun, 2002. Genomic effects of nucleotide substitutions in Drosophila simulans. Genetics 162**:** 1753–1761. [DOI] [PMC free article] [PubMed] [Google Scholar]
15. Kim, Y., and W. Stephan, 2000. Joint effects of genetic hitchhiking and background selection on neutral variation. Genetics 155**:** 1415–1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
16. Kim, Y., and W. Stephan, 2002. Detecting a local signature of genetic hitchhiking along a recombining chromosome. Genetics 160**:** 765–777. [DOI] [PMC free article] [PubMed] [Google Scholar]
17. Kim, Y., and W. Stephan, 2003. Selective sweeps in the presence of interference among partially linked loci. Genetics 164**:** 389–398. [DOI] [PMC free article] [PubMed] [Google Scholar]
18. Kimura, M., 1957. Some problems of stochastic processes in genetics. Ann. Math. Stat. 28**:** 882–901. [Google Scholar]
19. Kimura, M., 1983 The Neutral Theory of Molecular Evolution. Cambridge University Press, Cambridge, UK.
20. Kimura, M., and T. Ohta, 1969. The average number of generations until fixation of a mutant gene in a finite population. Genetics 61**:** 763–771. [DOI] [PMC free article] [PubMed] [Google Scholar]
21. Lande, R., and S. J. Arnold, 1983. The measurement of selection on correlated characters. Evolution 37**:** 1210–1226. [DOI] [PubMed] [Google Scholar]
22. Lynch, M., and J. B. Walsh, 1998 Genetics and Analysis of Quantitative Traits. Sinauer, Sunderland, MA.
23. Maynard Smith, J., and J. Haigh, 1974. The hitch-hiking effect of a favourable gene. Genet. Res. 23**:** 23–35. [PubMed] [Google Scholar]
24. Orr, H. A., 1991. A test of Fisher's theory of dominance. Proc. Natl. Acad. Sci. USA 88**:** 11413–11415. [DOI] [PMC free article] [PubMed] [Google Scholar]
25. Orr, H. A., and A. J. Betancourt, 2001. Haldane's sieve and adaptation from the standing genetic variation. Genetics 157**:** 875–884. [DOI] [PMC free article] [PubMed] [Google Scholar]
26. Otto, S., and M. C. Whitlock, 1997. The probability of fixation in populations of changing size. Genetics 146**:** 723–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
27. Przeworski, M., 2002. The signature of positive selection at randomly chosen loci. Genetics 160**:** 1179–1189. [DOI] [PMC free article] [PubMed] [Google Scholar]
28. Schlenke, T. B., and D. J. Begun, 2004. Strong selective sweep associated with transposon insertion in Drosophila simulans. Proc. Natl. Acad. Sci. USA 101**:** 1626–1631. [DOI] [PMC free article] [PubMed] [Google Scholar]
29. Steppan, S. J., P. C. Phillips and D. Houle, 2002. Comparative quantitative genetics: evolution of the G matrix. TREE 17**:** 320–327. [Google Scholar]