Ascertainment bias in studies of human genome-wide polymorphism (original) (raw)
Abstract
Large-scale SNP genotyping studies rely on an initial assessment of nucleotide variation to identify sites in the DNA sequence that harbor variation among individuals. This “SNP discovery” sample may be quite variable in size and composition, and it has been well established that properties of the SNPs that are found are influenced by the discovery sampling effort. The International HapMap project relied on nearly any piece of information available to identify SNPs—including BAC end sequences, shotgun reads, and differences between public and private sequences—and even made use of chimpanzee data to confirm human sequence differences. In addition, the ascertainment criteria shifted from using only SNPs that had been validated in population samples, to double-hit SNPs, to finally accepting SNPs that were singletons in small discovery samples. In contrast, Perlegen's primary discovery was a resequencing-by-hybridization effort using the 24 people of diverse origin in the Polymorphism Discovery Resource. Here we take these two data sets and contrast two basic summary statistics, heterozygosity and FST, as well as the site frequency spectra, for 500-kb windows spanning the genome. The magnitude of disparity between these samples in these measures of variability indicates that population genetic analysis on the raw genotype data is ill advised. Given the knowledge of the discovery samples, we perform an ascertainment correction and show how the post-correction data are more consistent across these studies. However, discrepancies persist, suggesting that the heterogeneity in the SNP discovery process of the HapMap project resulted in a data set resistant to complete ascertainment correction. Ascertainment bias will likely erode the power of tests of association between SNPs and complex disorders, but the effect will likely be small, and perhaps more importantly, it is unlikely that the bias will introduce false-positive inferences.
Because of the relatively low level of polymorphism in the human genome, the strategy for discovering SNPs by blanket resequencing of a small sample, followed by targeted genotyping of these SNPs in larger clinical samples, makes good economic sense (assuming the SNPs are still at sufficient density that one still has a good chance of detecting associations by linkage disequilibrium). This strategy worked well for identifying SNPs and patterns of linkage disequilibrium, but for subsequent population genetic analysis, not initially intended as a goal for the HapMap project, the data pose some challenges. The fact that the statistical properties of the genotype frequencies of the second sample differ from what one would see from full resequencing of that sample has been amply demonstrated (Kuhner et al. 2000; Wakeley et al. 2001 Akey et al. 2003; Nielsen and Signorovitch 2003; Nielsen 2004; Nielsen et al. 2004). This ascertainment bias results from the fact that the SNP discovery panel is often small, so that the probability that a SNP is identified in this sample is a function of the allele frequency. For example, if the discovery panel has only a size of two, then the chance of discovering a SNP with allele frequencies p and q is simply the chance that the two mismatch, or 2_pq_. This implies that rare SNPs are more likely to go undiscovered compared with common SNPs.
A consequence of this frequency-specific distortion in SNP discovery is that the frequency spectrum obtained from the two-tier sampling will be different from that obtained under complete sampling (e.g., by resequencing the entire study sample). As a result, any statistical attributes that rely on the site frequency spectrum (SFS)—including nucleotide diversity, Tajima's D, FST, and linkage disequilibrium—will be affected. For statistics that quantify nucleotide diversity, the effect of ascertainment bias is easily understood—because rare SNPs are missing, the average heterozygosity of the sites that are polymorphic is higher, and because SNPs are missing, the average heterozygosity across all sites is underestimated. The overrepresentation of sites of intermediate frequency means that Tajima's D will be biased upward unless the ascertainment bias is corrected. Among-population heterogeneity is generally underestimated with uncorrected data, in part because common SNPs are more likely to be shared across populations. But the situation is made more complex by the fact that the population composition of the discovery panel can result in overcalling or undercalling SNPs that are globally distributed.
Each individual SNP that is examined in the large sample may be accurately measured with respect to its frequency, heterogeneity among populations, and linkage disequilibrium. But ascertainment bias arises as a result of the SNPs that are missing from the larger sample. This implies that correction for ascertainment bias must be done by predicting properties of those missing SNPs, producing an ensemble of SNPs that would have been observed with complete sampling based on the ascertainment scheme and the properties of the ensemble of observed SNPs. Because the ascertainment correction is an ensemble prediction, it means that the correction must be based on groups of SNPs. The quality of the prediction depends in part on the sampling variance of the ensemble of SNPs, and so one gets better correction by examining larger collections of SNPs. This runs at odds with what one often wants to do in the analysis—make statements about individual genes or small genomic regions. Individual genes often have very little segregating variation, so full ascertainment correction on individual genes is problematic. As a compromise, here we apply the analysis to windows of 500 kb.
The intention here is to illustrate aspects of ascertainment bias by calculating simple descriptive statistics for the genome-wide HapMap (Gibbs et al. 2003) and Perlegen SNP data sets (Hinds et al. 2005), first taking the data at face value (with no ascertainment correction). The ascertainment schemes for these two samples are radically different, and we will show that the metrics for heterozygosity from these two samples are correspondingly quite disparate. We then show the ascertainment correction scheme for each sample, and how the post-correction statistics for heterozygosity and population heterogeneity are more concordant than were the pre-correction statistics. But the full site frequency spectra after ascertainment correction reveal important disparities between the HapMap and Perlegen data, suggesting that the known changes in the ascertainment procedures during the course of the study resulted in a complex mixture of ascertainment schemes that could not be fully corrected. A lingering difference between the African American sample from Perlegen and the Yoruban sample from HapMap has some important consequences for future association studies.
Results
No ascertainment correction
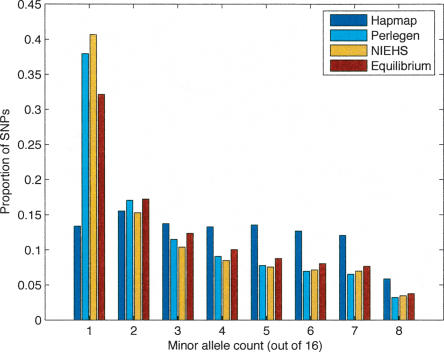
Figure 1 presents the site frequency spectra for the ascertainment samples from the HapMap and Perlegen studies and contrasts them to the NIEHS resequencing study (Livingston et al. 2004; http://egp.gs.washington.edu) and the neutral mutation-drift equilibrium expected. The figure depicts the subset of sites having sufficient sample size or “depth” (≥16), and for the SNPs with greater depth, sampling was done to place them on the figure. In the case of HapMap, only 6211 SNPs satisfied this depth criterion, but plots allowing lower depth had the same general appearance, namely, a large deficit of singletons and a large excess of SNPs whose frequency is ∼0.5. Perlegen's ascertainment by hybridization should have discovered many more than 1.6 M SNPs, but the procedure for SNP calling from their arrays was tuned to have a low false-positive rate (accepting a high false-negative rate). It is interesting to see how well this procedure avoided biasing the sample toward more common SNPs. The NIEHS data were obtained by complete resequencing, and so its departure from the neutral expectation is real. As many investigators have noted, the excess of rare SNPs likely has several causes, including population subdivision, population growth, and weak purifying selection (Ptak and Przeworski 2002; Williamson et al. 2005).
Figure 1.
Site frequency spectra for the fully resequenced NIEHS gene set, for the Perlegen sequencing-by-hybridization SNP ascertainment set, and for the set of SNPs that the International HapMap consortium genotyped, all contrasted to the neutral expectation (given estimates of the sample θ). Note the marked absence of rare SNPs and oversampling of SNPs of intermediate frequency in the HapMap sample.
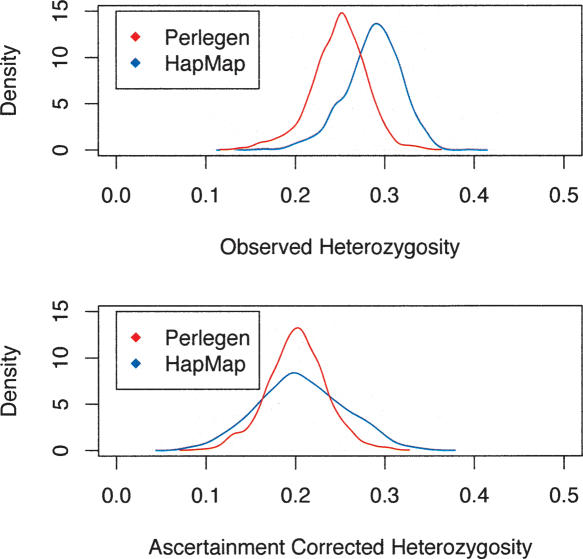
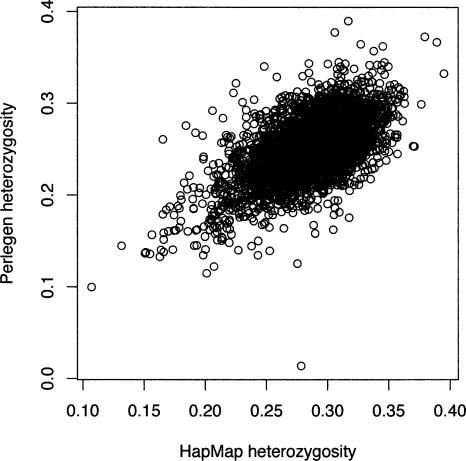
From the sets of ascertained SNPs, both the HapMap consortium and Perlegen genotyped a larger panel. A simple comparison of the HapMap and Perlegen genotype data was done by considering the 5682 windows of 500 kb across the entire genome and, for each window, tallying the SFS and calculating summary statistics such as average heterozygosity for each population and FST for each population pair and for the trio of samples. All statistics are calculated on a per-SNP basis rather than a per-nucleotide basis. Most windows of 500 kb appear to be adequate for this purpose, having an average of 122.8 and 214.8 SNPs for the HapMap and Perlegen samples, although 440 and 609 of the windows have <30 SNPs in the two samples (too few for accurate ascertainment correction). The average uncorrected heterozygosity within the three population groups for the HapMap data were 0.281, 0.247, and 0.268 for the Yoruban, Chinese, and European samples. The corresponding figures for the uncorrected Perlegen data are 0.251, 0.211, and 0.229 for the African American, Chinese, and European samples. Histograms of the average heterozygosity across the 500-kb windows (Fig. 2) show clearly that the HapMap data have a shift toward higher heterozygosity than do the Perlegen data. The reason for this is that the Perlegen ascertainment sample was 24 individuals, so that study captured more rare SNPs. When we plot the estimates of heterozygosity of pooled population samples for the HapMap versus the Perlegen samples, it is clear that the figures are correlated (r = 0.618, P < 2.2 × 10–16) (Fig. 3), but the scatter is greater than one gets by drawing two random subsamples from the same study. The ascertainment bias does not result in a perfectly smooth shift of the SFS, because, for the HapMap study, the ascertainment was highly heterogeneous across the 500-kb genomic windows. In fact, because of the way the SNP genotyping for the HapMap project was partitioned by chromosome among centers, there was great heterogeneity among chromosomes in SNP attributes. For example, chromosomes that were genotyped by Illumina had been resequenced to greater depth by the Sanger Institute, and so they were able to design assays of double-hit SNPs. As a result, these chromosomes displayed less skew to high frequency.
Figure 2.
(Top) Distributions of uncorrected HS (within-population heterozygosity) for the HapMap and the Perlegen data across 5682 windows of 500 kb spanning the entire human genome. Commensurate with the upward skew to the site frequency spectrum, the HapMap data have higher heterozygosity. (Bottom) After correction for ascertainment bias, the distributions of heterozygosity are more comparable; however, the ascertainment correction appears to have inflated the variance among windows in HS.
Figure 3.
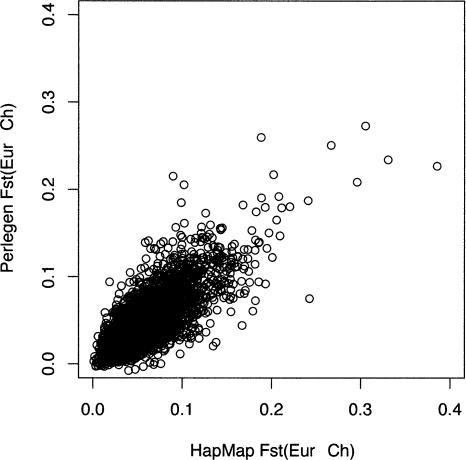
Scatterplot of uncorrected HT for the HapMap data (_x_-axis) and the Perlegen data (_y_-axis). Each circle represents a 500-kb window, and the plot depicts the entire HapMap and Perlegen genome-wide samples.
FST is a widely used metric for quantifying the proportion of the variance that occurs between population samples and is especially subject to ascertainment bias if SNPs are discovered in only one subpopulation. Uncorrected estimates of FST for Yoruban–Chinese and African American–Chinese (HapMap vs. Perlegen) are 0.111 versus 0.081, for Yoruban–European and African American–European are 0.099 versus 0.058, and for Chinese–European in the HapMap and Perlegen samples are 0.060 and 0.060. Note that the African American samples of Perlegen appear to show less genetic distance from the European samples than do the Yorubans, as expected due to admixture. This effect is large enough that it is clear even without ascertainment correction. The Chinese–European comparison is the only directly comparable one, since the samples of both HapMap and Perlegen contrast the CEPH samples to a sample of Han Chinese. In this case, the mean FST estimates of HapMap and Perlegen agree well.
Ascertainment correction
For each SNP in both data sets, we obtained information on the counts of the reference and variant nucleotide within each population group in the initial discovery panel. In the case of the HapMap data, we also had to incorporate the frequency filter, the application of the double-hit criterion to a subset of the SNPs, and the clustering of SNPs in sparse regions that were just single hits. These data were then used to estimate the probability of discovering each respective SNP, and these figures were then used to weight the frequencies to obtain an ascertainment-corrected frequency spectrum (Nielsen et al. 2004). Although the raw HapMap SNP data have a considerably higher heterozygosity than does the Perlegen sample (Fig. 2), with means 0.305 and 0.255, after ascertainment correction, the mean heterozygosities are very much more comparable (with means 0.180 and 0.186). Ascertainment correction results in lower estimates of heterozygosity because the small discovery sample is inferred to be missing the low-frequency SNPs that would otherwise pull down the average heterozygosity.
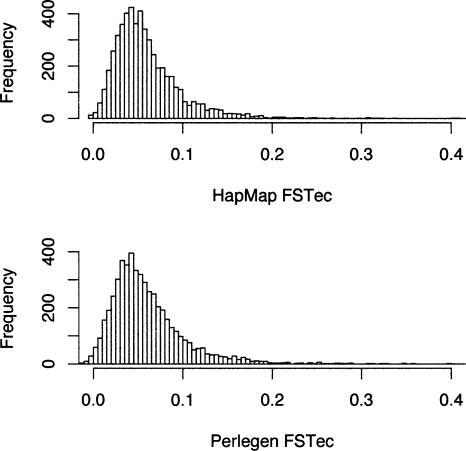
FST for the Yoruban–Chinese and African American–Chinese population pairs (in HapMap vs. Perlegen) are 0.097 and 0.063. For the Yoruban–European and African American–European population pairs, we get 0.086 versus 0.044, and for the Chinese–European population pair in the HapMap and Perlegen samples, the FST estimates are 0.055 and 0.055. The latter pair of population samples is the only directly comparable one, since the samples of both HapMap and Perlegen contrast the CEPH samples to a sample of Han Chinese. In this particular comparison, the HapMap and Perlegen data really do give remarkably consistent results (t = 0.0498, P = 0.96) (Fig. 4). The HapMap and Perlegen samples yield variation across 500-kb windows in the degree of Chinese–European heterogeneity, and the correlation in estimates of FST for this pair, after ascertainment correction, is quite high (r = 0.793, P = 2.2 × 10–16) (Fig. 5).
Figure 4.
Distributions of FST between European and Chinese samples for ascertainment-corrected 500-kb windows of the HapMap data (top) and the Perlegen data (bottom).
Figure 5.
Scatterplot of FST between European and Chinese samples for ascertainment-corrected 500-kb windows of the HapMap data vs. the Perlegen data.
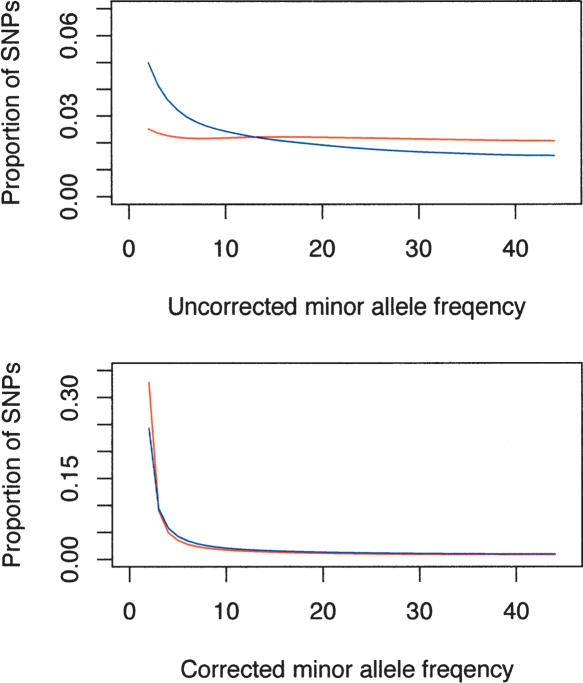
The most complete picture of how well the ascertainment correction procedure works to reflect unbiased samples from the population can be seen by plotting the site frequency spectra (Fig. 6). The uncorrected data display radical differences in the site frequency spectra of the Perlegen and HapMap data, while the corrected data go far to reducing this difference. There remain important differences, however, in the rare sites, possibly reflecting the incomplete information about the nonhomogeneous ascertainment in the HapMap project.
Figure 6.
Uncorrected (top) and ascertainment-corrected site frequency spectra (bottom) for the HapMap data (red)and the Perlegen data (blue dashed line). The HapMap data seriously underrepresented the rare SNPs compared with Perlegen, and the ascertainment correction produced frequency spectra that were more similar (bottom).
ENCODE regions
The ten 500-kb regions that constitute the ENCODE regions used by the HapMap project were fully resequenced in 16 CEPH (European), 16 Yoruban, eight Chinese, and eight Japanese people. Because we did not have Perlegen genotype data for Japanese, we used only the data from the first three populations. For each of the 10 regions, we calculated the heterozygosity and population heterogeneity statistics as before, except these data now constitute total ascertainment so the estimates are free of ascertainment bias. Table 1 contrasts the heterozygosity and FST statistics for these regions with the HapMap and Perlegen estimates, with and without ascertainment correction. It is very clear that the uncorrected HapMap data are badly biased upward in heterozygosity, and the Perlegen data are also upwardly biased. In both cases, the ascertainment correction reduced the estimates of heterozygosity and produced estimates that were closer to that observed in the full ENCODE data. Estimates of FST were more variable among regions with respect to their departure from the ENCODE data with, again, an upward bias in HapMap that was reasonably well controlled by the ascertainment correction.
Table 1.
Comparisons of the estimates of heterozygosity and FST of the 10 ENCODE regions, and the corresponding estimates in the same 500-kb windows of the HapMap and Perlegen data sets, with (asterisk) and without correction for ascertainment bias
| Region | H-enc | H-hapmap | H-hapmap* | H-perl | H-perl* | _FST_-enc | _FST_-hapmap | _FST_-hapmap* | _FST_-perl | _FST_-perl* |
|---|---|---|---|---|---|---|---|---|---|---|
| 2p16 | 0.243 | 0.305 | 0.199 | 0.282 | 0.202 | 0.076 | 0.080 | 0.073 | 0.079 | 0.068 |
| 2q37 | 0.259 | 0.319 | 0.217 | 0.280 | 0.188 | 0.112 | 0.122 | 0.105 | 0.091 | 0.073 |
| 4q26 | 0.213 | 0.334 | 0.178 | 0.326 | 0.255 | 0.126 | 0.146 | 0.119 | 0.069 | 0.056 |
| 7p15 | 0.193 | 0.305 | 0.196 | 0.277 | 0.199 | 0.103 | 0.126 | 0.115 | 0.095 | 0.079 |
| 7q21 | 0.170 | 0.262 | 0.144 | 0.253 | 0.168 | 0.089 | 0.110 | 0.081 | 0.086 | 0.068 |
| 7q31 | 0.177 | 0.297 | 0.194 | 0.262 | 0.207 | 0.096 | 0.107 | 0.092 | 0.104 | 0.081 |
| 8q24 | 0.194 | 0.318 | 0.210 | 0.264 | 0.183 | 0.106 | 0.113 | 0.102 | 0.076 | 0.063 |
| 9q34 | 0.187 | 0.312 | 0.176 | 0.344 | 0.274 | 0.138 | 0.141 | 0.118 | 0.107 | 0.087 |
| 12q12 | 0.205 | 0.299 | 0.208 | 0.267 | 0.202 | 0.049 | 0.053 | 0.049 | 0.065 | 0.054 |
| 18q12 | 0.182 | 0.282 | 0.183 | 0.304 | 0.254 | 0.083 | 0.083 | 0.076 | 0.070 | 0.058 |
Discussion
The magnitude of the differences between the estimates of heterozygosity and population subdivision in the HapMap and Perlegen samples in the absence of correction for ascertainment bias is substantial. The Perlegen SNP discovery approach was much more successful at capturing a representative sample of SNPs, although HapMap's ascertainment strategy successfully captured a greater proportion of SNPs of intermediate frequency. The initial design of HapMap was to provide a tool for testing association between common SNPs and risk of complex disorders, and for this purpose, one does want a sample biased toward more common SNPs. However, when one wants to apply HapMap data for other sorts of population genetic inference, this strongly biased sample needs to be used with caution.
The qualitative results are in excellent agreement with what was expected—namely, that the ascertainment scheme of HapMap resulted in a much greater overestimate of heterozygosity than did the ascertainment scheme for the Perlegen sample. The information on the ascertainment samples were generally adequate to provide acceptable corrections to the ascertainment bias, but the high variance across regions in the magnitude of pre- and post-ascertainment correction in the HapMap data is consistent with the wide heterogeneity in ascertainment designs and initial discovery sequencing depth. While the HapMap project suffered from this heterogeneity of ascertainment, the Perlegen project suffered from having to use the Polymorphism Discovery Resource (PDR), with its population-anonymous samples. Despite these problems, after ascertainment bias correction both data sets provide reasonably concordant estimates of heterozygosity and population heterogeneity for the bulk of the 500-kb windows examined.
A primary challenge in performing ascertainment correction occurs when there is uncertainty in the identities of individuals in the ascertainment panel, as occurred for the Perlegen sample. While this study had an excellent design in having a consistent discovery strategy across the entire genome, the PDR had been stripped of population identifiers so that the ascertainment correction had to consider possible different populations of origin for the individuals successfully scored for each SNP. There is a very large number of ways that n individuals can be drawn from a set of 24 when n is toward the middle of this range, so we had to resort to random sampling of these possibilities. It is clear that ascertainment correction is more efficient computationally, and it is more accurate if there is reliable information on the population of origin of each allele in the ascertainment panel.
While one would like to say that the scheme for ascertainment correction resulted in a perfect correspondence of the HapMap and Perlegen data, such is not the case. The distribution of heterozygosities across windows has greater variance in the HapMap sample compared with the Perlegen sample. One simple explanation could be sampling error. When the ascertainment sample often has just two sequences that mismatch (i.e., a single-hit SNP), then there is a large sampling variance to the expected frequency of this SNP. This sampling error increases the dispersion between the true SFS and the ascertainment-corrected SFS, and the result is a distribution of heterozygosities with a greater variance. But sampling is not the only reason for the greater variance in HapMap heterozygosities. The ascertainment depth varies greatly across genomic regions. It is also highly likely that the ascertainment data are not complete. While there was a good effort to keep track of which SNPs were ascertained by the double-hit criterion, the decision path for recruiting SNPs to the project changed radically during the project, and it is not always clear which SNPs had validation data prior to ascertainment decision. Finally, there is biological heterogeneity across the genome in attributes such as mutation rate, and the vagaries of sampling produce wide variation in the times to most recent common ancestry of different regions of the genome (Tavaré et al. 1997).
Given the challenges presented above, we can at least make some recommendations to minimize the errors introduced by ascertainment bias. First, of course, is to suggest that where possible one ought to strive to avoid the problem altogether by using fully sequenced random samples. DNA sequencing is sufficiently inexpensive that complete resequencing of targeted candidate genes can be done, at least for sample sizes in the hundreds or less. A few examples of this approach include the Seattle SNP project (Crawford et al. 2004), the Genaissance resequencing project (Stephens et al. 2001), the Applera SNP project (Bustamante et al. 2005), and the Arabidopsis 2010 project (Nordborg et al. 2005). The HapMap project hedged its bets by doing deeper resequencing of the ENCODE regions, and this provides an excellent opportunity to contrast the inferences made from the low-resolution, ascertainment-biased SNP data to the fully resequenced data. If one cannot obtain such complete resequencing data, then the best strategy is to maintain a uniform set of ascertainment criteria, keeping complete records of the discovery sample and using a large, well-documented discovery sample of known provenance.
Ascertainment bias affects any inference about the population that is based on the SFS of the SNPs. This includes many tests of natural selection that rely on distortions in the SFS to provide a signature for selection. In particular, Tajima's D will be affected, as would the tests of Fay and Wu (2000) and of Hudson et al. (1987). By selectively sampling SNPs of higher frequency, the genealogy of SNPs appears deeper than it should, driving back the time to most recent common ancestor. The degree of population differentiation may be either increased or decreased by ascertainment bias, depending on the ascertainment scheme. In general, the HapMap discovery sample was small and often had only individuals from one population. This overrepresents SNPs that are intermediate in frequency in one population and underrepresents SNPs that show large differences in allele frequency among populations. As a result, the post-correction FST values were shifted slightly lower were than the uncorrected values. Linkage disequilibrium is impacted in a complex way by ascertainment bias, but in general, the oversampling of common SNPs results in lower apparent LD (Nielsen and Signorovitch 2003).
There is concern that the ascertainment strategy that was applied to collect the SNPs for the HapMap project might impact subsequent use of the HapMap data for designing association tests. This is a topic that goes beyond the scope of this article, but some observations of the differences between HapMap and Perlegen and the magnitude of changes introduced by ascertainment bias correction are relevant. First, note that the biggest effect that ascertainment bias has is to avoid rare SNPs. The deficit of SNPs of low frequency means that the power to detect associations is reduced when the variants that actually cause the inflated risk are rare. On the other hand, the power to detect associations when the causal SNP is common is correspondingly increased. The original design of Hap Map was predicated on the Common Disease Common Variant (CDCV) hypothesis (see Kruglyak 1999; Pritchard 2001), and to the extent that CDCV is valid, the bias toward common SNPs would actually improve power. To the extent that the ascertainment protocol varies among regions of the genome, the power of association tests will vary correspondingly. One of the biggest concerns in doing whole-genome association testing is whether factors such as population stratification generate an excess of false positives (Pritchard and Rosenberg 1999). It would appear that the avoidance of rare SNPs, as is commonly observed in HapMap and other ascertainment schemes, will not result in inflation of false-positive rates for subsequent association tests, but this is an important problem worthy of additional study.
Methods
HapMap data
The SNP frequency data from the 5-kb resolution Phase I SNP map (Release 16c) of the International HapMap Project were downloaded from the Web site (www.hapmap.org). Ascertainment information, consisting of the counts of the alleles for each SNP in each of several discovery samples (including Celera) were kindly provided by Dr. James Mullikin (National Human Genome Research Institute [NHGRI]). Unfortunately, the process of ascertainment for the HapMap SNPs was very complicated, and it is probably impossible to fully reconstruct it. The initial information on human SNPs, assembled in dbSNP, was based on data from the genome project, from BAC end reads, from EST sequences, and from targeted resequencing projects. There was an effort to validate SNPs by genotyping in population samples, and early on, the HapMap project applied a frequency filter, only using SNPs with a minor allele >5%. Later there was too great a demand for new SNPs and no time for population-level validation, so the ascertainment switched to “double-hit” SNPs, meaning that the minor allele had to be observed twice. Subsequently, if the chimpanzee allele matched the minor allele in humans, then it was counted as valid for this double-hit criterion. Toward the end of the project, if regions of the genome had gaps >10 kb, then even single-hit SNPs (a single observation of the minor allele) were accepted. So the ascertainment procedure was a fairly complex moving target. The HapMap Web site has “SNP allocation files” that identify the double-hit SNPs, but it is not always easy to tell which SNPs were ascertained based on extrinsic validation data. Despite these problems, we can at least assemble the information to produce figures that reflect the alignment depth (sample size) in the discovery panel (Fig. S1), and compare it to that in the Perlegen sample.
The resequencing that was done to identify human polymorphisms was also quite heterogeneous. The Sanger Institute did resequencing to a 2× coverage for flow-sorted chromosomes, including 1, 6, 9–12 (as a pool), 13, 20, 22, and the X. Illumina made use of these data to identify double-hit SNPs for their bead platform. Some other chromosomes received greater resequencing from a single African American subject. In short, the ascertainment depth was quite variable among chromosomes.
Summary statistics for heterozygosity and population heterogeneity, described below, were calculated for each 500-kb window across the genome on the raw, uncorrected SNP frequencies. The X chromosome presented an especially challenging case for ascertainment correction and will be presented elsewhere. Based on the available information from the SNP allocation files and data from the DCC, we attempted to estimate the probability that each SNP would be discovered given the information at hand for the discovery process for each SNP. Collections of SNPs from each 500-kb window were subjected to ascertainment correction following the method of Nielsen et al. (2004), as outlined below.
Perlegen data
Allele frequency data were downloaded from the Perlegen Sciences Web site (http://genome.perlegen.com/browser/download.html), and ascertainment information was obtained directly from Drs. David Cox and David Hinds at Perlegen Sciences (www.perlegen.com). The genotypes in the sample discussed in Hinds et al. (2005) included SNPs discovered in dbSNP. In order to retain a consistent discovery panel, we limited our analysis to the SNPs that were discovered by Perlegen's chip-based resequencing, and we did not use any of the SNPs that Perlegen obtained from dbSNP to fill gaps. As for the HapMap data, the SNPs were collected in contiguous windows of 500 kb, and for each window an analysis was done both on the raw frequency counts and on the ascertainment-corrected counts. Although the sex of each individual in the PDR sample could be inferred from the data, there were still ambiguities in the reporting of X-linked SNP genotypes, so the X chromosome was not considered in this study. Ascertainment correction of the Perlegen data required sampling rather than exhaustive enumeration of all possible samples across populations of origin.
ENCODE data
The SNP genotypes of the 270 HapMap subjects for the ten 500-kb ENCODE regions were also downloaded (www.hapmap.org/downloads/encode1.html), and the observed heterozygosity and population heterogeneity statistics were calculated for these regions as well. The same regions were also pulled from the lower-density HapMap and Perlegen samples, and uncorrected and ascertainment-corrected estimates of heterozygosity and population heterogeneity were then compared with the estimates obtained from the fully sequenced ENCODE data (which should be free of ascertainment bias).
Heterozygosity, FST, and site frequency spectra
Define the frequencies of two alternative nucleotides at SNP j to be pj and qj =1 – pj. The estimator for heterozygosity is 2_piqi_[n/(n – 1)], where n is the sample size. The heterozygosity for a window is the simple arithmetic average of heterozygosities of the SNPs in that window. These heterozygosities were calculated for each of the three populations and were denoted at HSij, referring to the heterozygosity in subpopulation i for SNP j. For the pooled sample across the populations, we calculate the average (across populations) of allele frequencies (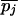 and
and 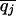 ), and define the total heterozygosity as
), and define the total heterozygosity as 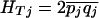 . FST can be thought of as the component of variance in allele frequency that is between populations, and Wright's approximate formula is FST =(HT – HS)/HT. To accommodate differences in sample size and pooling across SNPs, FST was calculated following the method of Weir (1996). Site frequency spectra were tallied by subsampling to produce counts that would be obtained given a fixed sample size of 30 (Nielsen et al. 2004).
. FST can be thought of as the component of variance in allele frequency that is between populations, and Wright's approximate formula is FST =(HT – HS)/HT. To accommodate differences in sample size and pooling across SNPs, FST was calculated following the method of Weir (1996). Site frequency spectra were tallied by subsampling to produce counts that would be obtained given a fixed sample size of 30 (Nielsen et al. 2004).
Ascertainment correction
Most of the modeling of ascertainment correction has assumed that there was a SNP discovery phase in which a strict set of criteria was applied to select which SNPs would be subsequently studied in the larger sample. The challenge in dealing with the HapMap data was that there was a changing set of nonuniformly applied criteria for selecting SNPs even after the SNP discovery data were collected. In addition, the process of SNP discovery itself varied widely across the genome. For these reasons, ascertainment correction required making a series of assumptions about the way the initial SNP discovery was made and how those data were interpreted to make the decision of which SNPs should be used in the full study. From Figure 1 it is abundantly clear that the SNPs were not drawn at random from the information of the discovery sample, but instead there was strong bias toward more common SNPs (i.e., in addition to the bias caused by the small size of the ascertainment panel). We know that this upward bias came in part from the use of extrinsic population validation data and also from application of the double-hit rule. But the ascertainment data clearly reveal that a sizable portion of SNPs did not satisfy the double-hit rule in the ascertainment sample, and we know that this happened with forethought to be able to fill in chromosomal gaps of sparse SNP density. It appears that the need to fill in gaps resulted in the greatest wavering from standard rules of ascertainment, and that these departures were clustered in the sparse SNP regions. Fortunately, records were kept to identify which SNPs had double-hit ascertainment.
For each 500-kb window, we calculated the SFS for the SNPs in the window (for both HapMap and Perlegen samples). We use information regarding the allele frequencies in the ascertainment samples, and the sample size of the ascertainment sample for each SNP in order to do obtain the corrected frequency spectrum. The corrections are done by using the maximum likelihood method described in equation 2 of Nielsen et al. (2004). In the case of joint analyses of data from two populations, the method is applied to the two-dimensional frequency spectrum with _m_1_m_2 – 1 categories for two populations with samples sizes _m_1 and _m_2. Missing data are taken into account by explicitly summing over all possible configurations of the missing data in the calculation of the likelihood function.
Acknowledgments
We thank David Cox and David Hinds (Perlegen Sciences) for their efforts to describe the SNP discovery process used by Perlegen Sciences. Dr. James Mullikin kindly provided the data on ascertainment from the HapMap datacenter and clarified many aspects of the HapMap ascertainment process. Kevin Thornton and Bret Payseur provided useful suggestions during the analysis. This work was supported by NIH grants GM65509, HL072904, and HG03229 to C.D.B., R.N., and A.G.C.
[Supplemental material is available online at www.genome.org.\]
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.4107905\. Freely available online through the Genome Research Immediate Open Access option.
References
- Akey, J.M., Zhang, K., Xiong, M., and Jin, L. 2003. The effect of single nucleotide polymorphism identification strategies on estimates of linkage disequilibrium. Mol. Biol. Evol. 20**:** 232–242. [DOI] [PubMed] [Google Scholar]
- Bustamante, C.D., Fledel-Alon, A., Williamson, S., Nielsen, R., Hubisz, M.T., Glanowski, S., Tanenbaum, D.M., White, T.J., Sninsky, J.J., Hernandez, R., et al. 2005. Natural selection on protein coding genes in the human genome. Nature (in press). [DOI] [PubMed]
- Crawford, D.C., Carlson, C.S., Rieder, M.J., Carrington, D.P., Yi, Q., Smith, J.D., Eberle, M.A., Kruglyak, L., and Nickerson, D.A. 2004. Haplotype diversity across 100 candidate genes for inflammation, lipid metabolism, and blood pressure regulation in two populations. Am. J. Hum. Genet. 74**:** 610–622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fay, J.C. and Wu, C.I. 2000. Hitchhiking under positive Darwinian selection. Genetics 155**:** 1405–1413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibbs, R.A., Belmont, J.W., Hardenbol, P., Willis, T.D., Yu, F., Yang, H., Chang, L.-Y., Huang, W., Liu, B., Shen, Y., et al. 2003. The International HapMap Project. Nature 426**:** 789–796. [DOI] [PubMed] [Google Scholar]
- Hinds, D.A., Stuve, L.L., Nilsen, G.B., Halperin, E., Eskin, E., Ballinger, D.G., Frazer, K.A., and Cox, D.R. 2005. Whole-genome patterns of common DNA variation in three human populations. Science 307**:** 1072–1079. [DOI] [PubMed] [Google Scholar]
- Hudson, R.R., Kreitman, M., and Aguadé, M. 1987. A test of neutral molecular evolution based on nucleotide data. Genetics 116**:** 153–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruglyak, L. 1999. Prospects for whole-genome linkage disequilibrium mapping of common disease genes. Nat. Genet. 22**:** 139–144. [DOI] [PubMed] [Google Scholar]
- Kuhner, M.K., Beerli, P., Yamamoto, J., and Felsenstein, J. 2000. Usefulness of single nucleotide polymorphism data for estimating population parameters. Genetics 156**:** 439–447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Livingston, R.J., Von Niederhausern, A., Jegga, A.G., Crawford, D.C., Carlson, C.S., Rieder, M.J., Gowrisankar, S., Aronow, B.J., Weiss, R.B., and Nickerson, D.A. 2004. Pattern of sequence variation across 213 environmental response genes, Genome Res. 14**:** 1821–1831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen, R. 2004. Population genetic analysis of ascertained SNP data. Hum. Genomics 1**:** 218–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen, R. and Signorovitch, J. 2003. Correcting for ascertainment biases when analyzing SNP data: Applications to the estimation of linkage disequilibrium. Theor. Pop. Biol. 63**:** 245–255. [DOI] [PubMed] [Google Scholar]
- Nielsen, R., Hubisz, M.J., and Clark, A.G. 2004. Reconstituting the frequency spectrum of ascertained single-nucleotide polymorphism data. Genetics 168**:** 2373–2382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordborg, M., Hu, T.T., Ishino, Y., Jhaveri, J., Toomajian, C., Zheng, H., Bakker, E., Calabrese, P., Gladstone, J., Goyal, R., et al. 2005. The pattern of polymorphism in Arabidopsis thaliana. PLoS. Biol. 3**:** e196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard, J.K. 2001. Are rare variants responsible for susceptibility to complex diseases? Am. J. Hum. Genet. 69**:** 124–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard, J.K. and Rosenberg, N.A. 2002. Use of unlinked genetic markers to detect population stratification in association studies. Am. J. Hum. Genet. 65**:** 220–228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ptak, S.E. and Przeworski, M. 2002. Evidence for population growth in humans is confounded by fine-scale population structure. Trends Genet. 18**:** 559–563. [DOI] [PubMed] [Google Scholar]
- Stephens, J.C., Schneider, J.A., Tanguay, D.A., Choi, J., Acharya, T., Stanley, S.E., Jiang, R., Messer, C.J., Chew, A., Han, J.H., et al. 2001. Haplotype variation and linkage disequilibrium in 313 human genes. Science 293**:** 489–493. [DOI] [PubMed] [Google Scholar]
- Tavaré, S., Balding, D.J., Griffiths, R.C., and Donnelly, P. 1997. Inferring coalescence times from DNA sequence data. Genetics 145**:** 505–518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakeley, J., Nielsen, R., Liu-Cordero, S.N., and Ardlie, K. 2001. The discovery of single-nucleotide polymorphisms—and inferences about human demographic history. Am. J. Hum. Genet. 69**:** 1332–1347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weir, B.S. 1996. Genetic data analysis II. Sinauer Associates, Sunderland, MA.
- Williamson, S.H., Hernandez, R., Fledel-Alon, A., Zhu, L., Nielsen, R., and Bustamante, C.D. 2005. Simultaneous inference of selection and population growth from patterns of variation in the human genome. Proc. Natl. Acad. Sci. 102**:** 7882–7887. [DOI] [PMC free article] [PubMed] [Google Scholar]
Web site references
- http://egp.gs.washington.edu; NIEHS resequencing study.
- http://www.hapmap.org; International HapMap Project.
- http://genome.perlegen.com/browser/download.html; Perlegen Sciences Web site.
- http://www.hapmap.org/downloads/encode1.html; HapMap .subjects