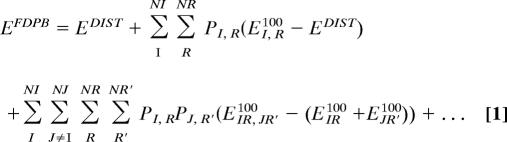Accurate, conformation-dependent predictions of solvent effects on protein ionization constants (original) (raw)
Abstract
Predicting how aqueous solvent modulates the conformational transitions and influences the pKa values that regulate the biological functions of biomolecules remains an unsolved challenge. To address this problem, we developed FDPB_MF, a rotamer repacking method that exhaustively samples side chain conformational space and rigorously calculates multibody protein–solvent interactions. FDPB_MF predicts the effects on pKa values of various solvent exposures, large ionic strength variations, strong energetic couplings, structural reorganizations and sequence mutations. The method achieves high accuracy, with root mean square deviations within 0.3 pH unit of the experimental values measured for turkey ovomucoid third domain, hen lysozyme, Bacillus circulans xylanase, and human and Escherichia coli thioredoxins. FDPB_MF provides a faithful, quantitative assessment of electrostatic interactions in biological macromolecules.
Keywords: conformational flexibility, electrostatics, pKa prediction, protein modeling
By strongly interacting with charges, the solvent significantly modulates the electrostatic properties of biomolecular systems. Although variations in pH and ionic strength are responsible for physiologically important conformational transitions (1), quantitatively assessing their role in modulating electrostatic energies is particularly challenging (2). Approaches in which solvent is modeled as a continuum polarizable medium while biomolecules are modeled in explicit molecular detail have become widely used in recent years (3, 4). However, no current method combines broad conformational sampling with a rigorous solvation model that can predict quantitatively and efficiently the effects of solvent on protein energetics and conformations.
In principle, molecular dynamics and free-energy simulations monitoring protonation events can model accurately the energetic effects of solvation and conformational relaxation of biomolecules. However, despite recent progress, these techniques often fail to converge in a reasonable amount of computer time and therefore do not provide reliable predictions of thermodynamic properties (5, 6).
Rotamer repacking methods sample more efficiently and exhaustively the conformational space of biomolecules. However, these methods require the energy function be decomposed into self energies and interaction energies between pairs of residues (7–10). Consequently, repacking methods cannot model the effects of conformational relaxations involving more than two positions at a time. Many important properties of biomolecular surfaces (i.e., their interface with the solvent and the distribution of bulk ions around them) are not pairwise factorable and depend on the simultaneous knowledge of the conformations of all residues. Approximating these effects by relaxing the protein–solvent interface only at the vicinity of solvent-exposed charged residues does not improve the prediction of pKa values in proteins (11). Current rotamer repacking methods have also difficulties in assessing accurately and reliably the electrostatic properties of buried charged residues that often play important roles in catalysis, structural specificity, and folding (2, 9–11).
To address these problems, we developed FDPB_MF, a rotamer repacking method that combines a general and full treatment of side chain conformational flexibility with the rigorous computation of multibody protein–solvent interactions. Non-pairwise factorable solvation energy terms calculated by a finite-difference Poisson–Boltzmann (FDPB) method were incorporated into a mean-field (MF) side chain rotamer repacking algorithm. Side chain conformations that minimize the free energy of the system were identified with the explicit relaxation of the protein–solvent interface and of the ion distribution around the protein. Here, we apply FDPB_MF to the classic problem of calculating the ionization constants of protein side chains.
Results
For further details, see supporting information (SI) Text, SI Figs. 4–7, and SI Tables 5–8.
FDPB_MF was developed to provide a solution to the problem of combining efficiently the exhaustive sampling of protein side chain conformations with a rigorous treatment of solvation. The method is based on an ensemble description in which each conformation is assigned a weight corresponding to its probability of being occupied in the population. The effective quantities describing the probability-weighted conformational ensembles were derived so that they would equate or well approximate the corresponding average calculated by enumerating all of the discrete states of the system. During the development of the method, three important challenges were encountered that led to algorithmic developments for accurate calculation of the solvation energy of a probability-weighted conformational ensemble [Eq. 1 and SI Fig. 5], calculation of probability-dependent physical quantities to solve the Poisson-Boltzmann equation (SI Text Eqs. S2 and S4) and mapping of probability-weighted dielectric boundaries on a lattice (SI Text Eqs. S6 and S7 and SI Fig. 6).
Choice of the Solute Dielectric Constant.
The choice of a dielectric constant for the solute (εp) depends on the level of explicit modeling of its polarizabilities. εp = 2 is commonly assumed to be an adequate value for the implicit average treatment of electronic polarizabilities. Because electronic fluctuations and backbone conformational relaxations are not treated explicitly in FDPB_MF, the solute was assigned a higher εp of 4, a value derived from crystalline acetamide, a molecular analogue of the protein backbone (12). However, no sets of atomic charges and radii with εp = 4 have been parameterized to reproduce solvation energies of peptides or proteins. The closest set of parameters is the PARSE set, parameterized to reproduce solvation energies of small molecules with solute polarizabilities corresponding to εp ranging from 2 to 3 (13). In principle, the calculations should be performed with the εp of the molecules from which the PARSE set of charges and radii were derived. Table 1 summarizes the prediction of the pKa values of OMTKY3 by FDPB_MF performed with εp = 2 or 4. The predictions with εp = 2 were still acceptable (rmsd = 0.5) but significantly less accurate than the ones performed with εp = 4, especially for the buried Asp-27 (rms error of 0.9 versus 0.0). The main reasons for the reduced accuracy could be
- FDPB_MF's treatment of polarizability due to conformational relaxation of the polypeptide chain is limited to the effects of sampling side chain rotameric degrees of freedom. The use of εp = 4 may compensate for the lack of treatment of backbone conformational relaxation and covalent bond distortions and also for the discrete representation of the conformational space.
- Solvation due to electronic polarizability may be higher in protein cores than in highly solvated small molecules and would explain why the loss of accuracy mainly affected the buried Asp-27.
- With εp = 2, the difference in solvation energies and electrostatic interactions between solvent-exposed and buried positions are higher than with εp = 4. The ruggedness of the conformational free energy landscape may therefore be higher with εp = 2 than with εp = 4. Accordingly, the self-consistent MF (SCMF) algorithm did not always well converge at εp = 2 and this may also explain why the predictions were less accurate. To ensure convergence, the lambda factor (SI Fig. 4 and ref. 15) which controls the rotamer probability updates in the SCMF was subsequently lowered to 0.15 in all of the calculations performed in this study. In these calculations, the solute and the solvent were also always assigned a dielectric constant of 4 and 80, respectively.
Table 1.
Effect of the solute dielectric constant on the pKa values calculated for OMTKY3
| Sites | ||||||||
|---|---|---|---|---|---|---|---|---|
| Asp-7 | Glu-10 | Glu-19 | Asp-27 | Glu-43 | C terminus | rms error | Max error | |
| Experimental* | 2.7 ± 0.06 | 4.1 ± 0.07 | 3.2 ± 0.02 | 2.2 ± 0.06 | 4.8 ± 0.1 | <2.7 ± 0.12 | ||
| FDPB_MF† (εp‡ = 4) | 2.5 | 3.9 | 3.0 | 2.3 | 4.4 | 2.7 | 0.2 | 0.4 |
| FDPB_MF† (εp‡ = 2) | 2.5 | 4.5 | 2.6 | 3.2 | 5.1 | 2.7 | 0.5 | 0.9 |
Test of the FDPB_MF Algorithm.
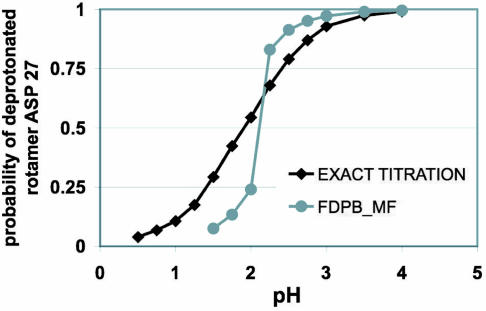
To validate the physical basis of the approach, we performed energy calculations and conformational searches on a model OMTKY3 with three flexible polar sites that we could enumerate discretely. Effective solvation energies were found to be within 0.3 kcal/mol of the exact probability-weighted average energies of the discrete states of the system (data not shown). The ability of the FDPB_MF algorithm to find pH-dependent global free energy minima also was assessed. The FDPB_MF titration curves were compared with the exact curve obtained by exhaustively sampling all of the microstates of the system (Fig. 1). The pKa of Asp-27 predicted by FDPB_MF in the model OMTKY3 lies within 0.3 pH unit of the value calculated by using the exact scheme. However, the variations in the probability of the deprotonated species upon pH predicted by FDPB_MF were much sharper than the one predicted by enumerating all of the microstates of the system. Asp-27 protonated and deprotonated species interact strongly with two different conformations of Tyr-31 (see SI Fig. 7_A_). This strong conformational coupling could not be resolved by a simple mean-field averaging of the conformational ensembles (zero- and first-order terms of Eq. 1) (16, 17). At pH values close to the pKa, where these mutually exclusive configurations have similar free energies, FDPB_MF only selects the configuration that has the lowest free energy. To accurately compute the probability of each chemical specie at pH values close to the pKa, protonated and deprotonated states for this residue pair have to be enumerated and treated separately (second-order term in Eq. 1). The second-order term in Eq. 1 also proved to be essential in the accurate prediction of the pKas of the two buried energetically coupled glutamate residues of Bacillus circulans xylanase.
Fig. 1.
Accuracy of the convergence of the FDPB_MF compared with the solution obtained by exhaustively sampling all of the discrete states of the system. The two different predicted titration curves of Asp 27 correspond to the sum of the probability of the deprotonated rotamers of Asp-27 as a function of the pH. The “exact titration” curve (black) was obtained by enumerating all of the discrete states of the system and is equal to the sum at a given pH of the Boltzmann weights of the discrete states occupied by the deprotonated rotamers. The FDPB_MF curve (gray) is derived by relaxing a rotameric probability distribution with the FDPB_MF method. It corresponds to the probability that minimizes at a given pH the electrostatic free energy of the protein after optimization by the SCMF algorithm.
Prediction of Solvent-Dependent Protein Ionization Constants.
We then assessed the ability of FDPB_MF to accurately predict solvent-dependent energetics in proteins. For all FDPB_MF predictions, conformational flexibility was modeled for side chains atoms, whereas backbone atoms were fixed to the coordinates determined by x-ray crystallography. The resulting conformational ensemble was relaxed by the SCMF algorithm to find the distribution of rotamer probabilities that minimizes the free energy of the system. The pKa values were assigned to the pH at which the corresponding sites become 50% deprotonated.
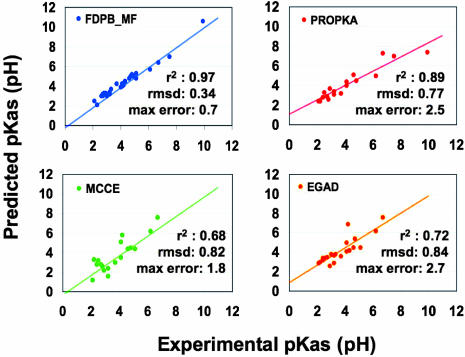
Fig. 2 summarizes the pKa calculations performed by FDPB_MF on 31 acidic residues and compares these values to the predictions published by other methods. Among these, PROPKA performs best, with a rmsd, maximal error to the experimental values and correlation coefficient of 0.77 pH unit, 2.5 pH units, and 0.89, respectively. However, the slope of the best fit to these predictions was significantly lower than 1.0 (0.73), suggesting that the model underlying PROPKA has been trained to reproduce experimental data rather than accurately recapitulating first physical principles. FDPB_MF predicts the pKa values with a rmsd, maximal error to the experimental values and correlation coefficient of 0.34 pH unit, 0.70 pH unit, and 0.97, respectively. The slope of the best fit to these predictions was 1.01. We largely focused our study on functionally or structurally important residues with pKas that are often difficult to predict accurately (Table 2). PROPKA surpasses other published methods with a rmsd and maximal error to the experimental values of 0.89 unit and 2.5 pH units, respectively. FDPB_MF predicts the pKa values with a rmsd, maximal error to the experimental values of 0.38 and 0.70 pH unit, respectively.
Fig. 2.
Synopsis of the pKa predictions performed by FDPB_MF and comparison with other methods: PROPKA (18), MCCE (10), and EGAD (9). rsmds and maximal errors to the experimental values are in pH units. Each line and _r_2 value corresponds to the best linear regression fit to the data and the correlation coefficient, respectively.
Table 2.
Comparison between experimental and calculated pKa values for structurally and functionally important sites
| Protein | Sites | Experiment* | FDPB_MF† (εp‡ = 4) | PROPKA§ | MCCE¶ (εp‡ = 4) | EGAD‖ (εp‡ = 8) | FDPB**(εp‡ = 20) | Null model†† |
|---|---|---|---|---|---|---|---|---|
| OMTKY3 | D7 | 2.7 | 3.1 | 2.8 | 2.8 | 3.1 | 2.9 | 4.0 |
| I = 10 mM | D27 | 2.2 | 2.1 | 2.4 | 3.3 | 3.0 | 3.6 | 4.0 |
| E19 | 3.2 | 3.2 | 3.1 | 1.6 | 3.7 | 2.6 | 4.4 | |
| I = 1 M | D7 | 3.3 | 3.7 | ND | ND | ND | 3.5 | 4.0 |
| D27 | 2.9 | 3.0 | ND | ND | ND | 4.0 | 4.0 | |
| E19 | 4.0 | 3.9 | ND | ND | ND | 3.0 | 4.4 | |
| HEWL | D52 | 3.7 | 4.3 | 3.2 | 3.0 | 3.6 | 3.1 | 4.0 |
| D87 | 2.1 | 2.5 | 2.4 | 1.2 | 2.9 | 2.7 | 4.0 | |
| E7 | 2.9 | 3.3 | 3.7 | 2.2 | 2.6 | 3.3 | 4.4 | |
| E35 | 6.2 | 5.7 | 5.0 | 6.2 | 6.2 | 4.4 | 4.4 | |
| BCX | E78 | 4.6 | 4.8 | 5.1 | ND | 4.4 | 2.9 | 4.4 |
| E172 | 6.7 | 6.4 | 7.3 | ND | 7.6 | 5.9 | 4.4 | |
| E172Q | E78 | 5.1 | 5.0 | ND | ND | 4.5 | 4.3 | 4.4 |
| E78Q | E172 | 4.2 | 3.8 | ND | ND | 6.9 | 2.8 | 4.4 |
| TRX | D26 | 7.5 | 7.0 | 7.0 | ND | ND | 5.8 | 4.0 |
| TRH | D26 | 9.9 | 10.6 | 7.4 | ND | ND | 7.5 | 4.0 |
| rmsd | 0.38 | 0.89 | 0.92 | 0.98 | 1.24 | 2.11 | ||
| Max error | 0.7 | 2.5 | 2.6 | 2.7 | 2.4 | 5.9 |
The ionic strength is an important parameter governing the stability and function of proteins. Several acidic sites of OMTKY3 show measured pKa shifts of 0.25–0.77 pH unit upon variation of the ionic strength from 10 mM to 1 M (19). FDPB_MF accurately predicted the effects of such large variation in ionic strength (Table 3). The rmsd and the maximum error to the experimental values were 0.14 and 0.2 pH unit, respectively. The sensitivity of pKas to the change in bulk ionic strength often reflects the nature of the electrostatic interactions stabilizing a particular ionized site (30, 31). These results suggest that FDPB_MF predicts quantitatively the complex balance of electrostatic interactions that stabilize charged residues.
Table 3.
Experimental and calculated ionic strength effects on the pKa values of OMTKY3
| Sites | |||||||
|---|---|---|---|---|---|---|---|
| Asp-7 | Glu-10 | Glu-19 | Asp-27 | Glu-43 | rms error | Max error | |
| Experimental* | 0.57 ± 0.2 | 0.25 ± 0.14 | 0.77 ± 0.05 | 0.72 ± 0.1 | 0.30 ± 0.14 | ||
| FDPB_MF† (εp = 4) | 0.63 | 0.40 | 0.74 | 0.90 | 0.10 | 0.14 | 0.25 |
| FDPB‡ (εp = 20) | 0.58 | 0.54 | 0.41 | 0.43 | 0.14 | 0.21 | 0.47 |
Accurately predicting the energetic effects of mutations is an important goal in protein modeling. The insensitivity of the pKas of three acidic residues (Asp-7, Glu-10, Glu-19) to the removal of a neighboring positively charged residue (Lys 34) was not accurately predicted by simple FDPB calculations (20). FDPB_MF predicted smaller pKa perturbations (Table 4), with rmsd and maximal error from the experimental data of 0.28 and 0.4 pH unit, respectively.
Table 4.
Experimental and calculated effects of point mutations on the pKa values of OMTKY3
| Mutant | Sites | ||||
|---|---|---|---|---|---|
| Asp-7 | Glu-10 | Glu-19 | rms error | Max error | |
| Lys34Gln | |||||
| Experimental* | −0.1 ± 0.1 | 0.15 ± 0.14 | 0.1 ± 0.1 | ||
| FDPB_MF† (εp = 4) | 0.3 | 0.4 | 0.2 | 0.28 | 0.4 |
| FDPB‡ (Xray, εp = 20) | 0.6 | 0.4 | 0.6 | 0.52 | 0.7 |
| Lys34Thr | |||||
| Experimental* | 0 ± 0.3 | 0.15 ± 0.1 | −0.1 ± 0.1 | ||
| FDPB_MF† (εp = 4) | 0.3 | 0.4 | 0.2 | 0.28 | 0.3 |
| FDPB‡ (X-ray, εp = 20) | 0.6 | 0.4 | 0.6 | 0.55 | 0.7 |
Electrostatic interactions play a crucial role in modulating the catalytic reactivity of enzymes. We assessed the ability of FDPB_MF to accurately predict the pKa values of the two buried energetically coupled glutamate residues that lie at the heart of the active site of B. circulans xylanase (BCX; Table 2 and SI Table 8). Simple FDPB calculations with a single dielectric constant of 8 for the protein failed to predict accurately the pKa values of both glutamates in the WT protein. By introducing an explicit treatment of conformational flexibility, EGAD performed better than FDPB and similar to PROPKA for the WT protein. However, EGAD failed to predict the large pKa shift (−2.5 pH units) observed for Glu-172 when Glu-78 was mutated to Gln (21, 22). By finely sampling the conformational space in the vicinity of the glutamates and by uncoupling their titration in the WT protein, FDPB_MF accurately predicted the unusually high pKa of Glu-172 (pKa of 6.7) and its large pKa shift upon mutation of Glu-78 to Gln. The rmsd and maximal error to the experimental values were equal to 0.2 and 0.3 pH unit, respectively.
The buried, catalytically important Asp-26 in Escherichia coli and human thioredoxins have among the highest pKa values ever measured for an aspartate (23). FDPB_MF predicted their pKa more accurately than other methods, with errors of 0.5 and 0.7 pH unit compared with the experimental values (Table 2 and SI Table 8).
Prediction of Solvent-Dependent Protein Conformations.
Because protein energetics and conformations are tightly coupled, we expect quantitative energetic predictions to be corroborated with high-resolution structural predictions.
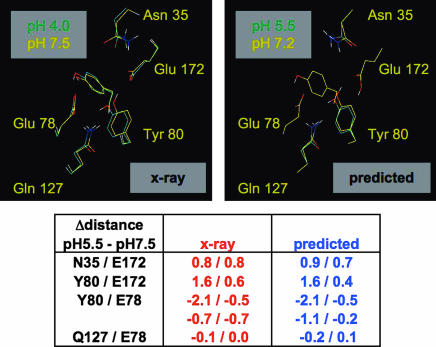
Fig. 3 compares the observed and predicted structural reorganizations occurring in the active site of B. circulans xylanase upon titration of Glu 172. Although the crystals were soaked at pH 4.0, the observed conformation at “pH 4.0” likely corresponds to that induced by deprotonated Glu 78 and protonated Glu 172 (21) and can be compared with the structure predicted at pH 5.5. Except for a small difference at Tyr 69, the observed and predicted conformational changes induced by protonation of Glu 172 are in good agreement. The aromatic ring of Tyr 80 flips by 180° to preferentially stabilize the remaining deprotonated Glu at position 78. The Asn 35 amide group moves away from the protonated Glu 172 and the amide of Gln 127 comes slightly closer to Glu 78. The rmsd between the predicted and observed distance changes involving protons and heteroatoms in the active site was 0.2 Å (SI Table 5).
Fig. 3.
Good agreement between observed and predicted conformational changes induced by the protonation of Glu 172 in B. circulans xylanase. Figures were generated by using Pymol (www.delanoscientific.com). As discussed in ref. 21, the crystal structure solved at an apparent pH of 4.0 is likely to be consistent with Glu 172 being protonated. Protons on the x-ray structures were added with the program Reduce (32). At the bottom, distance changes are provided in angstroms. The first and second numbers represent distances between protons and heteroatoms and distances between heteroatoms, respectively.
FDPB_MF also predicted substantial pH dependent conformational shifts (SI Text and SI Fig. 7) that have yet to be tested by experiments. Most of these conformational changes were corroborated with significantly improved energetic predictions when compared with traditional FDPB calculations performed on fixed crystallographic structures (Tables 2–4 and SI Tables 6–8).
Discussion
Protein stability, solubility, recognition, and catalysis depend critically on electrostatic interactions, and many important conformational transitions in proteins are triggered physiologically by changes in bulk ion composition and in pH. FDPB_MF was developed to accurately predict this coupling between solvent-dependent protein energetics and conformations. Here we used FBPB_MF to predict the pKa values of 31 carboxylates in very different protein environments and solvent conditions. This approach yielded predictions of unprecedented accuracy as well as new capabilities to model the effects of mutations and changes in ionic strength. The accuracy of the pKa predictions approached the experimental error in the measured values, adding considerable utility to the pKa predictions based on structural data.
For charged residues near the protein surface, the solvent accessibility and solvation energies are mainly determined by the conformation of neighboring residues or substrates. By explicitly modeling the conformational relaxations of all residues and/or ligands that constitute the protein-solvent interface, the FDPB_MF method captures the energetics of partially solvent-exposed acidic residues more accurately than available methods that rely solely on pairwise-factorable energy functions. Buried charged residues are less frequent and are often involved in catalysis or in structural specificity. Anisotropy in polarizability of protein interiors is higher than at the surfaces, in line with the inability of FDPB calculations to capture implicitly the structural relaxation of protein interiors with a single dielectric constant (21). The energetics of buried residues are therefore sensitive to the fine conformational reorganization of their packed microenvironments. FDPB_MF explicitly models these effects and predicts the energetics of buried charged residues more accurately than current molecular dynamics simulations and rotamer repacking methods. The accuracy of FBPB_MF arises from the unique combination of fine sampling of the side chain conformational space, rigorous calculation of multibody protein–solvent interactions and a general treatment of conformational relaxation. Unlike current methods based on first principles, FDPB_MF quantitatively predicts the energetic effects of various protein environments, sequence mutations and solvent compositions (Fig. 2, rmsd from experimental values = 0.34 pH unit). Each calculation reported here took 2–6 days on a single Pentium 4 2.4 GHz CPU for a single pH.
Understanding the relationships between protein energetics, conformations and dynamics also presents major challenges in protein modeling. Proteins exhibit side chain conformational flexibility that is dictated by their structural environment and by the physical properties of the solvent. FDPB_MF predicts pH-induced, side chain conformational changes involving either changes in the dominant rotamers or redistribution of probabilities within a conformational ensemble (Fig. 3 and SI Fig. 7). These shifts highlight the complex nature of the electrostatic interactions involved in stabilizing charged residues. The explicit modeling of these structural reorganizations by FDPB_MF is corroborated by improved energetic predictions when compared with fixed-structure calculations (Tables 2–4 and SI Tables 6–8). The pH-induced conformational changes predicted by FDPB_MF in B. circulans xylanase are in good agreement with those observed in the crystals (Fig. 3). As the challenges of protein structure prediction continue to move toward the generation of high-resolution models (33), the accurate prediction of solvent-dependent conformational changes will grow in importance.
Materials and Methods
FDPB Calculations.
Perturbation theory is an effective approach for the computation of mean-field properties and correlations beyond the mean-field. Following the same formalism (i.e., in the form of a perturbation series), Eq. 1 describes a general solution to the electrostatic protein–solvent interaction energy (EFDPB) of a conformational ensemble defined by a rotamer probability distribution (PI,R).
In this ensemble description, each rotamer is assigned a weight corresponding to its probability of being occupied in the population of rotamers. In the mean-field approximation, individual side chain rotamers interact with the probability-weighted average of all of the rotamers at the neighboring sites. The corresponding mean-field electrostatic protein–solvent interaction energies are defined by the zero- and first-order terms of Eq. 1. These were computed in two steps by the FDPB module (SI Fig. 5). First, all side chain rotamers R at all sites I weighted by their probabilities PI,R were mapped onto a three-dimensional grid. The Poisson–Boltzmann (PB) equation was solved by finite-differences for this “distributed” conformational ensemble and a corresponding solvation energy, EDIST, was computed (zero-order term in Eq. 1). This “distributed” representation of the system is inaccurate partly because rotamers from the same site are present and interact with each other. An additional energy term for each rotamer, E_100_IR (first-order term in Eq. 1), is necessary and was computed by iteratively placing single discrete rotamers at each site and solving the PB equation for the solvation energy. Adding the first-order to the zero-order term of Eq. 1 corrects for the simultaneous presence of rotamers on the grid and gives an accurate solution to the mean-field protein–solvent electrostatic interaction energies. The mean-field treatment was sufficient for most calculations performed in this study. It failed, however, when side chain conformations from different sites were strongly coupled. Higher-order terms in Eq. 1 are then necessary to describe the mutually exclusive combinations of rotamers.
The mean-field treatment requires the definition of effective physical quantities that accurately describe the probability-weighted conformational ensembles. These quantities were derived so that they would equate or well approximate the corresponding average calculated by enumerating all of the discrete states of the system. If a rotamer R alone occupies a particular space with a probability _P_R, it is equivalent to that space being occupied a fraction _P_R of the time by the solute and a fraction (1 − _P_R) of the time by the solvent. Consequently, if _E_R, _E_S, and _E_W define the Born solvation energy of a charge covered by rotamer R, pure solute, or water, respectively, then _E_R should equate the probability weighted average of _E_S and _E_W as defined by Eq. 2
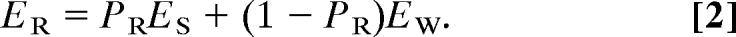
Eq. 2 was used to derive the effective physical quantities needed to solve the PB equation by finite differences for the probability-weighted conformational ensembles (SI Text).
The FDPB algorithm is based on the QNIFFT program (Academic version of Delphi provided by K. Sharp, University of Pennsylvania, Philadelphia, PA). All calculations were carried out on a 129 cubic grid. Focusing yielded grid resolutions > 2.4 grid units/Å (34). The linearized form of the PB equation was solved by the inexact Newton method with a multilevel solver algorithm to aid convergence (35). The solute was mapped on the grid with PARSE charge and radii parameters (13). Atomic charges, dielectric constants, and Debye factors were assigned according to the probabilities of occupancy of the solute and water (SI Text). A 1.4-Å water sphere probe radius and a 2.0-Å Stern ion-exclusion radius were used to generate the solvent-accessible surface and ion exclusion layer, respectively. Solvation energies were calculated by subtracting the energy of the grid computed for the solute placed in solvent from the energy of the same grid computed without solvent in a medium of uniform dielectric constant.
Conformational Search.
A SCMF method was developed that relaxes a side chain rotamer probability distribution to minimize the free energy of a protein conformational ensemble (15). In this method, non-pairwise factorable protein–solvent electrostatic interactions were computed repeatedly as rotamer probabilities were updated (SI Fig. 4). At each iteration of the relaxation, a new rotamer probability distribution (PM1) was sent to the FDPB module, and the algorithm computed protein–solvent electrostatic interaction energies for that particular rotamer probability distribution. These quantities were combined with precomputed one- and two-body nonelectrostatic potential energy terms to calculate mean-field potential energies (_E_ir).
pKa Predictions.
Proteins were described by a conformational ensemble consisting of a fixed backbone and a library of side chain rotamers at each flexible position. For all calculations, fixed backbone and side chain coordinates were taken from the x-ray structures 1PPF (25), 1XNB (26), 2TRX (27), 1ERT (28), and 2LZT (29) for OMTKY3, BCX, TRX, TRH, and HEWL, respectively. The penultimate rotamer library (36) was used to model side chain conformational flexibility for all amino acids. Side chain coordinates were built on the backbone structure and energy minimized by using the CHARMM19 geometric and van der Waals potential energy terms and a 20° square well dihedral restraint (37). Protonated rotamers for acidic residues were built by placing the proton trans to the preceding methylene group. The entropic bias for the protonated state was corrected by adding the quantity RT × log(_N_p/_N_d) to the mean-field energy of the protonated rotamers (_N_p and _N_d being the number of protonated and deprotonated rotamers at a given site, respectively).
The modeling of side chain flexibility was defined in each system to keep the calculations efficient while adequately sampling conformational space (SI Text). In the minimalist OMTKY3 system, three neighboring polar residues (Asp-27, Lys-29, and Tyr-31) were treated simultaneously with several side chain rotamers weighted by probabilities lying between but not equal to 0 and 1. All other sites were placed in the discrete side chain crystallographic coordinates.
In addition to the electrostatic solvation term (_U_FDPB), the potential energy function was approximated and decomposed in pairwise-factorable potential energy terms
where _U_geom and _U_LJ correspond, respectively, to the bonded and Lennard–Jones energy terms of the CHARMM19 force field (37). _U_SAS corresponds to the pairwise-factorable approximation of the nonelectrostatic solvation potential derived from the product over the solvent surface tension and the solvent-accessible surface area of the solute (38). _U_protonation consists of a protonation potential and is derived from a thermodynamic cycle relating a titratable site in the protein to the equivalent site in an isolated model compound with an experimentally determined pKa (12).
Relaxations of the conformational ensembles were performed by the SCMF algorithm at several pHs varying by steps of 0.25 pH unit. The pKa of a particular site was assigned to the pH at which the probabilities of the deprotonated and protonated rotamers become equal.
Supplementary Material
Supporting Information
Acknowledgments
We thank J. Havranek for sharing a program for side chain conformational search that was useful in the initial steps of the project. We are grateful to Lawrence McIntosh for drawing our attention to and providing unpublished coordinates on the xylanase system, to Ho-Leung Ng and Mark Sales for critical reading of the manuscript, and to the anonymous reviewers for their suggestions. This work was supported by National Institutes of Health Grant GM48958 (to T.A.).
Abbreviations
PB
Poisson–Boltzmann
FDPB
finite-difference PB
MF
mean-field
SCMF
self-consistent MF
OMTKY3
turkey ovomucoid third domain
BCX
B. circulans xylanase
TRX
E. coli thioredoxin
HEWL
hen lysozyme.
Footnotes
The authors declare no conflict of interest.
References
- 1.Garcia-Moreno BE, Fitch CA. Methods Enzymol. 2004;380:20–51. doi: 10.1016/S0076-6879(04)80002-8. [DOI] [PubMed] [Google Scholar]
- 2.Schutz CN, Warshel A. Proteins. 2001;44:400–417. doi: 10.1002/prot.1106. [DOI] [PubMed] [Google Scholar]
- 3.Baker NA. Methods Enzymol. 2004;383:94–118. doi: 10.1016/S0076-6879(04)83005-2. [DOI] [PubMed] [Google Scholar]
- 4.Baker NA. Curr Opin Struct Biol. 2005;15:137–143. doi: 10.1016/j.sbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 5.Mongan J, Case DA. Curr Opin Struct Biol. 2005;15:157–163. doi: 10.1016/j.sbi.2005.02.002. [DOI] [PubMed] [Google Scholar]
- 6.Simonson T, Carlsson J, Case DA. J Am Chem Soc. 2004;126:4167–4180. doi: 10.1021/ja039788m. [DOI] [PubMed] [Google Scholar]
- 7.Marshall SA, Vizcarra CL, Mayo SL. Protein Sci. 2005;14:1293–1304. doi: 10.1110/ps.041259105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Havranek JJ, Harbury PB. Proc Natl Acad Sci USA. 1999;96:11145–11150. doi: 10.1073/pnas.96.20.11145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pokala N, Handel TM. Protein Sci. 2004;13:925–936. doi: 10.1110/ps.03486104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Georgescu RE, Alexov EG, Gunner MR. Biophys J. 2002;83:1731–1748. doi: 10.1016/S0006-3495(02)73940-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Warwicker J. Protein Sci. 2004;13:2793–2805. doi: 10.1110/ps.04785604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Antosiewicz J, McCammon JA, Gilson MK. Biochemistry. 1996;35:7819–7833. doi: 10.1021/bi9601565. [DOI] [PubMed] [Google Scholar]
- 13.Sitkoff D, Sharp KA, Honig B. J Phys Chem. 1994;98:1978–1988. [Google Scholar]
- 14.Schaller W, Robertson AD. Biochemistry. 1995;34:4714–4723. doi: 10.1021/bi00014a028. [DOI] [PubMed] [Google Scholar]
- 15.Koehl P, Delarue M. J Mol Biol. 1994;239:249–275. doi: 10.1006/jmbi.1994.1366. [DOI] [PubMed] [Google Scholar]
- 16.Bashford D, Karplus M. J Phys Chem. 1991;95:9556–9561. [Google Scholar]
- 17.Spassov VZ, Bashford D. J Comput Chem. 1999;20:1091–1111. [Google Scholar]
- 18.Li H, Robertson AD, Jensen JH. Proteins. 2005;61:704–721. doi: 10.1002/prot.20660. [DOI] [PubMed] [Google Scholar]
- 19.Forsyth WR, Gilson MK, Antosiewicz J, Jaren OR, Robertson AD. Biochemistry. 1998;37:8643–8652. doi: 10.1021/bi980187v. [DOI] [PubMed] [Google Scholar]
- 20.Forsyth WR, Robertson AD. Biochemistry. 2000;39:8067–8072. doi: 10.1021/bi992967p. [DOI] [PubMed] [Google Scholar]
- 21.Joshi MD, Sidhu G, Nielsen JE, Brayer GD, Withers SG, McIntosh LP. Biochemistry. 2001;40:10115–10139. [PubMed] [Google Scholar]
- 22.Joshi MD, Hedberg A, McIntosh LP. Protein Sci. 1997;6:2667–2670. doi: 10.1002/pro.5560061224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Langsetmo K, Fuchs JA, Woodward C, Sharp KA. Biochemistry. 1991;30:7609–7614. doi: 10.1021/bi00244a033. [DOI] [PubMed] [Google Scholar]
- 24.Bartik K, Redfield C, Dobson CM. Biophys J. 1994;66:1180–1184. doi: 10.1016/S0006-3495(94)80900-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bode W, Wei AZ, Huber R, Meyer E, Travis J, Neumann S. EMBO J. 1986;5:2453–2458. doi: 10.1002/j.1460-2075.1986.tb04521.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Campbell RL, Rose DR, Wakarchuk WW, To RJ, Sung W, Yaguchi M, Suominen P, Reinikainen T, editors. Proceedings of the Second TRICEL Symposium on Trichoderma reesei Cellulases and other Hydrolases, Espoo, Finland, 1993; Helsinki, Finland: Found Biotech Indust Fermentation Res; 1993. pp. 63–72. [Google Scholar]
- 27.Katti SK, LeMaster DM, Eklund H. J Mol Biol. 1990;212:167–184. doi: 10.1016/0022-2836(90)90313-B. [DOI] [PubMed] [Google Scholar]
- 28.Weichsel A, Gasdaska JR, Powis G, Montfort WR. Structure (London) 1996;4:735–751. doi: 10.1016/s0969-2126(96)00079-2. [DOI] [PubMed] [Google Scholar]
- 29.Ramanadham M, Sieker LC, Jensen LH. Acta Crystallogr B. 1990;46:63–69. doi: 10.1107/s0108768189009195. [DOI] [PubMed] [Google Scholar]
- 30.Kao YH, Fitch CA, Bhattacharya S, Sarkisian CJ, Lecomte JT, Garcia-Moreno EB. Biophys J. 2000;79:1637–1654. doi: 10.1016/S0006-3495(00)76414-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kuhlman B, Luisi DL, Young P, Raleigh DP. Biochemistry. 1999;38:4896–4903. doi: 10.1021/bi982931h. [DOI] [PubMed] [Google Scholar]
- 32.Word JM, Lovell SC, Richardson JS, Richardson DC. J Mol Biol. 1999;285:1735–1747. doi: 10.1006/jmbi.1998.2401. [DOI] [PubMed] [Google Scholar]
- 33.Bradley P, Misura KM, Baker D. Science. 2005;309:1868–1871. doi: 10.1126/science.1113801. [DOI] [PubMed] [Google Scholar]
- 34.Gilson MK, Sharp KA, Honig B. J Comput Chem. 1987;9:327–335. [Google Scholar]
- 35.Holst M, Saied F. J Comput Chem. 1995;16:337–364. [Google Scholar]
- 36.Lovell SC, Word JM, Richardson JS, Richardson DC. Proteins. 2000;40:389–408. [PubMed] [Google Scholar]
- 37.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. J Comput Chem. 1983;4:187–217. [Google Scholar]
- 38.Street AG, Mayo SL. Fold Des. 1998;3:253–258. doi: 10.1016/S1359-0278(98)00036-4. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information