The Effects of Force Inhibition by Sodium Vanadate on Cross-Bridge Binding, Force Redevelopment, and Ca2+ Activation in Cardiac Muscle (original) (raw)

Abstract

Strongly bound, force-generating myosin cross-bridges play an important role as allosteric activators of cardiac thin filaments. Sodium vanadate (Vi) is a phosphate analog that inhibits force by preventing cross-bridge transition into force-producing states. This study characterizes the mechanical state of cross-bridges with bound Vi as a tool to examine the contribution of cross-bridges to cardiac contractile activation. The _K_i of force inhibition by Vi was ∼40 _μ_M. Sinusoidal stiffness was inhibited with Vi, although to a lesser extent than force. We used chord stiffness measurements to monitor Vi-induced changes in cross-bridge attachment/detachment kinetics at saturating [Ca2+]. Vi decreased chord stiffness at the fastest rates of stretch, whereas at slow rates chord stiffness actually increased. This suggests a shift in cross-bridge population toward low force states with very slow attachment/detachment kinetics. Low angle x-ray diffraction measurements indicate that with Vi cross-bridge mass shifted away from thin filaments, implying decreased cross-bridge/thin filament interaction. The combined x-ray and mechanical data suggest at least two cross-bridge populations with Vi; one characteristic of normal cycling cross-bridges, and a population of weak-binding cross-bridges with bound Vi and slow attachment/detachment kinetics. The Ca2+ sensitivity of force (pCa50) and force redevelopment kinetics (_k_TR) were measured to study the effects of Vi on contractile activation. When maximal force was inhibited by 40% with Vi pCa50 decreased, but greater force inhibition at higher [Vi] did not further alter pCa50. In contrast, the Ca2+ sensitivity of _k_TR was unaffected by Vi. Interestingly, when force was inhibited by Vi _k_TR increased at submaximal levels of Ca2+-activated force. Additionally, _k_TR is faster at saturating Ca2+ at [Vi] that inhibit force by >∼70%. The effects of Vi on _k_TR imply that _k_TR is determined not only by the intrinsic properties of the cross-bridge cycle, but also by cross-bridge contribution to thin filament activation.

INTRODUCTION

In addition to being the molecular motors responsible for force generation and shortening in cardiac muscle, myosin cross-bridges contribute to thin filament activation in the presence of activating [Ca2+]. As such they are an important component of contractile regulation in cardiac muscle. The cross-bridge contribution to thin filament activation occurs following Ca2+ binding to cardiac troponin C (cTnC) and the subsequent displacement of the troponin-tropomyosin (Tn/Tm) complex into a position on the thin filament surface that is permissive to cross-bridge binding to actin (for review see Gordon et al. (1)). Cross-bridges that make the transition from the weak initial attachment to strong binding, force-generating states contribute to activation by at least two mechanisms in cardiac muscle. First, strong cross-bridges either stabilize or displace Tn/Tm further toward the “open” state on the thin filament surface, resulting in exposure of additional cross-bridge binding sites on actin (2–4). Second, strong cross-bridge binding allosterically increases the apparent affinity of Tn for Ca2+. The latter is evidenced by a reduction in Ca2+ binding to cardiac thin filaments (5,6) and reduction of Ca2+-induced structural changes in fluorescently labeled cTnC in skinned cardiac trabeculae (7,8) following inhibition of force with the phosphate analog sodium vanadate (Vi). Together these mechanisms constitute a positive feedback path that contributes to the steepness and apparent cooperativity of the cardiac force-[Ca2+] relationship (9).

Because maximal Ca2+-activated force is strongly inhibited by Vi in skinned cardiac muscle, Vi has been an important tool for isolating the effects of cross-bridges on thin filament activation from those of Ca2+ binding to TnC. However, whereas previous studies have used millimolar concentrations of Vi to maximally inhibit force and strong cross-bridge binding, intermediate levels of inhibition may provide important information to further elucidate the mechanisms by which strong cross-bridge/thin filament interaction contributes to cardiac contractile regulation. However, the effects of Vi on cross-bridge/thin filament interaction at intermediate levels of force inhibition have not been characterized. Vi could inhibit force by either altering the properties of the entire ensemble of cross-bridges or by shifting the partition of cross-bridge states from strong to weak binding during Ca2+ activation. Therefore, if Vi is used to probe the contribution of strong cross-bridge binding to cardiac thin filament activation at intermediate levels, it is necessary to characterize its effects not only on force generation, but on the distribution of cross-bridges between states that bind weakly or strongly to thin filaments. The latter is necessary to interpret effects of Vi inhibition of cross-bridge binding on parameters that monitor changes in thin filament activation, such as Ca2+ sensitivity of force (pCa50) and the rate of isometric force redevelopment (_k_TR). In this study we characterized cross-bridge properties at intermediate levels of force inhibition by Vi using mechanical measurements of force and stiffness, as well as low angle x-ray diffraction to monitor corresponding changes in cross-bridge mass distribution between thick and thin filaments. We further used Vi to study the mechanisms by which cross-bridge binding determines both pCa50 and the activation dependence of _k_TR in skinned trabeculae from rats.

Increasing [Vi] inhibited force and sinusoidal stiffness, with force being inhibited to a greater degree than stiffness. Chord stiffness was used to characterize the kinetics of thick-thin filament interaction. The data indicate Vi binding to cardiac myosin inhibits force by increasing a population of weak-binding cross-bridges that exhibit slowed attachment/detachment kinetics. Surprisingly, Vi increased _k_TR at submaximal Ca2+ activation, and at saturating [Ca2+] when force was inhibited by >70%. Taken together the results indicate that Vi inhibits force by partitioning cross-bridges between weak-binding cross-bridge states and those with normal cycling kinetics. Furthermore elevation of _k_TR at submaximal and maximal forces suggests that _k_TR reflects not only the intrinsic kinetics of the actomyosin interaction but also the interaction of cross-bridges with the thin filament regulatory apparatus. Preliminary reports of this work have been published previously (10).

METHODS

Preparation

Male Sprague-Dawley rats (150–250 gram) were anesthetized with an intraperitoneal injection of pentobarbital (50 mg/kg). Animals were housed in the Department of Comparative Medicine and all procedures were done in accordance with the rules and procedures of the University of Washington Animal Care Committee. Their hearts are rapidly dissected and placed in oxygenated physiological salt solution. Trabeculae (160 ± 10 _μ_m diameter, 1.4 ± 0.1 mm length) were dissected from the right ventricle and chemically skinned by exposure to a bathing solution containing (in mM): 100 KCl, 9.0 MgCl2, 4.0 MgATP, 5.0 K2EGTA (ethylene glycol-bis-(b-aminoethylether)-N,N,_N_9,_N_9-tetraacetic acid), 10 MOPS (3-(_n_-morpholino) propane sulfonic acid), 1% nonionic detergent Triton X-100, pH 7.0, and 50% v/v glycerol for at least 30 min at room temperature. The skinned trabeculae were stored in the same solution without Triton X-100 at −20°C and used for experiments within 1 week. Experimental temperature was 15°C. Ionic strength was 170 mM.

Solutions

Solution composition was determined according to an iterative computer program that calculates the equilibrium concentration of ligands and ions based on published affinity constants. Proprionate was the major anion. Relaxing solutions contained (in mM): 80 MOPS, 15 EGTA; 1 Mg2+; 5 MgATP; 52 Na+; 83 K+; 15 creatine phosphate (CP); and 20 units/ml creatine phosphokinase (CPK), pH 7.0. Rigor solutions contained no MgATP, CP, or CPK. For activation solutions, the Ca2+ level (expressed as pCa = −log [Ca2+]) was set by adjusting Ca(propionate)2. Sodium vanadate stock (100 mM) was prepared as described by Goodno (11). Inorganic phosphate (Pi) was elevated by adding Na2HPO4 to bathing solutions. Solutions containing elevated MgADP had no CPK or CP, but contained 10 mM ATP along with a myokinase inhibitor (AP5A; Sigma/Aldrich Chemical, St. Louis, MO) to minimize enzymatic breakdown of added ADP.

Mechanical apparatus

Trabeculae ends were wrapped in aluminum foil T-clips for attachment to a force transducer (model AE801, ≥5-kHz resonant frequency [SensoNor]) and a servo-motor (model 300, Cambridge Technology, Lexington, MA) tuned for a 300-_μ_s step response. Trabeculae were placed in a 200-_μ_L temperature controlled well. Sarcomere length (SL) was measured with helium-neon laser diffraction and set at either 2.3 or 2.0 _μ_m in relaxing solution (pCa 9.0). A detailed description of our mechanical apparatus can be found in Martyn and Chase (12). Chord stiffness was determined using stretches of 0.5% muscle length (ML) at varying rates and monitoring the resulting increase of force during the stretches (13). Stiffness was measured as the ratio of dF/dt to dML/dt during the period of stretch. During chord K measurements data were filtered to prevent frequency aliasing and acquired at rate that was dependent on the rate of stretch and digitized at 12-bit resolution for analysis with customer software. Sinusoidal stiffness was determined by sinusoidal length oscillations (±0.15 %ML) at 500 Hz. The baseline for isometric force was measured by transiently shortening the fiber to slack length; relaxed passive force was subtracted from active force. The rate of force redevelopment (_k_TR) was measured following a ramp release (−4 ML/s; 15 %ML) followed by a rapid (<350 _μ_s) restretch to the initial length, as described in Adhikari et al. (14); _k_TR was determined from the half-time of force redevelopment as described by Chase et al. (13).

X-ray experiments

Low angle x-ray diffraction measurements were done with single skinned trabeculae at beamline X27C, National Synchrotron Light Source, Brookhaven National Laboratories, Upton, NY. The beamline characteristics and apparatus are described in Xu et al. (15) and in Martyn et al. (16). Briefly, chemically skinned right ventricular trabeculae were placed in an upright chamber in which solutions can be exchanged and the preparation exposed to a high intensity synchotron x-ray source. The chamber volume was 0.5 ml and solutions were continuously stirred with a perfusion pump. To minimize preparation damage due to x-ray exposure the entire chamber was translated along the fiber axis so that most of the length of the trabeculae was interrogated by the beam. Total exposure time was limited to 4 min for each preparation. Equatorial intensity from both sides of the meridian of the equatorial x-ray pattern was summed and the (1,1) and (1,0) intensity profiles were scanned and integrated. Integrated intensities and spacings of the equatorial 1,0 and 1,1 diffraction peaks were determined using PeakFit (SPSS, Chicago, IL).

Data analysis

Force-pCa data were fit by the Hill equation,

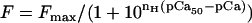
graphic file with name M1.gif

where _F_max is the maximally activated force, _n_H is the Hill coefficient or slope, and pCa50 is the pCa at which force is half-maximal. The reported pCa50 and _n_H values represent the means of the values from the individual fits, mean ± SE. Means are compared with Student's _t_-test with significance at the 95% confidence level (P < 0.05). Statistical analysis was performed using Excel (Microsoft, Redmond, WA), SigmaPlot (Systat, Richmond, CA), and PeakFit (SPSS).

RESULTS

The effect of [Vi] on maximal Ca2+-activated isometric force in rat single skinned trabeculae was determined by the protocol described in Fig. 1. Initial sarcomere length was 2.3 _μ_m. First, the fiber was transferred from a relaxing solution (pCa 9.0) to preactivating solution with low [EGTA] (0.1 mM), followed by maximal activating solution (pCa 4.5) and then pCa 4.5 solution with Vi added. This protocol was used because exposure of the fiber to Vi in relaxing solution before Ca2+ activation for any length of time up to 30 min did not inhibit force. Force was only inhibited if the preparation was exposed to Vi during Ca2+ activation, as shown for skeletal fibers (17,18). Following exposure to pCa 4.5 plus Vi, the fiber was relaxed and the sarcomere length readjusted to 2.3 _μ_m, if necessary. This was followed by placing the trabecula in a series of solutions containing increasing [Ca2+] to allow determination of the force-pCa relation, with 0.3 mM Vi added to each solution. The fiber was then washed in relaxing solution with no Vi and allowed to develop force at pCa 4.5 with no Vi. Recovery from Vi inhibition was 79 ± 3% (n = 5). The final rise of force took significantly longer than the rise of force during the initial activation without Vi, as we have previously observed for skinned skeletal fibers (18). In each solution, sinusoidal stiffness, _k_TR and chord stiffness were measured. The maximal Ca2+-activated force at 2.0 _μ_m SL for all preparations was 29.8 ± 5.6 mN/mm2 (n = 10). The effects of Vi on stiffness were assessed at 2.0 _μ_m SL because at this length passive force and its contribution to the sinusoidal and chord-stiffness measurements were minimal. Qualitatively similar stiffness data were obtained at 2.3 _μ_m SL in all cases (data not shown).

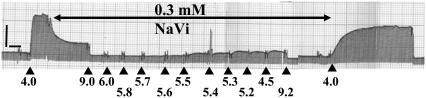
FIGURE 1.

FIGURE 1

Force was maximally activated at pCa 4.5. After steady-state force was reached, force was inhibited with 0.3 mM Vi, followed by relaxation in pCa 9.2. Force was subsequently measured at various submaximal [Ca2+] (indicated below the force trace), each with 0.3 mM Vi. The trabeculae was again relaxed. The relaxed trabecula was finally activated in pCa 4.5 to allow force recovery (typically >80%). Initial sarcomere length was 2.3 _μ_m and diameter was 125 _μ_M. The calibration bars represent 30 mg (vertical) and 1 min (horizontal).

Care must be taken to limit the [Vi] used to inhibit force because exposure of skinned cardiac muscle to high concentrations of Vi (10 mM) has been shown to extract whole troponin, causing Ca2+-insensitive active force (19). However it is unlikely that troponin was extracted from the preparations used in this study because resting force (pCa 9.2) after Vi treatment and following recovery from force inhibition, was completely unaffected by Vi concentrations from 0.05 to 1.0 mM, as shown in Fig. 1 (0.3 mM Vi.).

The effects of force inhibition by Vi on force, sinusoidal stiffness, and _k_TR at saturating [Ca2+]

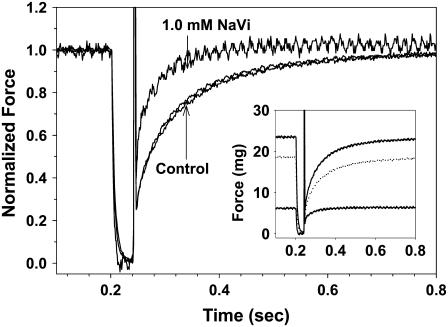
Examples of force traces obtained during _k_TR measurements are shown in Fig. 2 at pCa 4.5, in the absence and presence of 1.0 mM Vi, and following recovery from inhibition. The steady-state force was reduced to 23% of control with inhibition and recovered to 79% following washout of Vi. In Fig. 2 force is normalized to the maximum for each condition to emphasize differences in force redevelopment kinetics (the inset shows the original force traces). Interestingly, _k_TR was faster in the presence of 1.0 mM Vi compared to control solutions.

FIGURE 2.

FIGURE 2

Representative traces of force redevelopment following the rapid release/restretch protocol used to determine _k_TR are shown; _k_TR was determined during steady force at each [Ca2+] and [Vi]. Force was normalized to the maximum for each condition and is shown for preinhibition controls, following force inhibition by 1.0 mM Vi and subsequent to force recovery from Vi inhibition. The time course of force development in controls and following recovery from inhibition nearly superimpose. The corresponding unnormalized traces are shown in the inset; _k_TR was 15.9 s−1 in pC 4.5 controls, 23 s−1 with 1.0 mM Vi and 14.9 s−1 following recovery from inhibition in pCa 4.5.

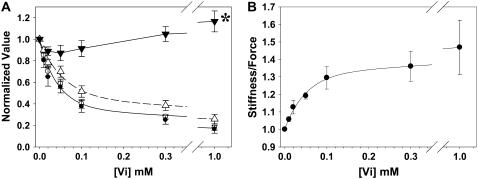
The effect of [Vi] on maximal Ca2+-activated force (_F_max), sinusoidal stiffness, and _k_TR are illustrated in Fig. 3 A. The data are normalized to values obtained in the absence of Vi for each condition. _F_max was inhibited with increasing [Vi] (_K_i of ∼40 _μ_M) at both 2.0 and 2.3 _μ_m SL. Sinusoidal stiffness also decreased with increasing [Vi], (_K_d = ∼60 _μ_M), but to a lesser extent than force. This apparent difference in the sensitivity of force and stiffness to Vi is emphasized in Fig. 3 B, where the ratio of stiffness/force increases substantially at higher [Vi] and lower force. In contrast to force and stiffness, at intermediate [Vi] (0.02–0.3 mM) maximal _k_TR was not significantly different from controls. However, at higher [Vi] (1.0 mM) force was only 17 ± 2.0% (n = 5 trabeculae) of control, while _k_TR increased from 21.5 ± 2.7 s−1 to 24.6 ± 2.8 s−1 (P < 0.05). Combined, these data suggest that Vi decreased cross-bridge binding, but that cross-bridge cycling rates (_k_TR) may be unaffected or increased at saturating [Ca2+].

FIGURE 3.

FIGURE 3

The dependence of force on [Vi] with maximal activating [Ca2+] (pCa 4.5) at SL = 2.3 (•) and 2.0 (○) _μ_m, along with sinusoidal stiffness (▵) at 2.0 _μ_m initial SL, is illustrated in A. Also shown in A is the dependence of the maximal rate of isometric force redevelopment (_k_TR; ▾) on [Vi] at SL = 2.0 _μ_m. At pCa 4.5 with 1.0 mM Vi, _k_TR (▾*) was significantly faster than control (P < 0.05). All variables in panel A have been normalized to the corresponding values obtained at pCa 4.5 without Vi; data were obtained from seven trabeculae. The force and stiffness data in A are replotted in B to illustrate Vi effects on the stiffness/force ratio at pCa 4.5 and 2.0 _μ_m SL.

The effect of increasing [Vi] on chord stiffness

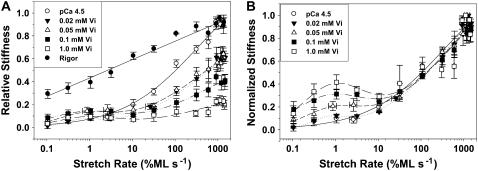
Measurements of chord stiffness have been used to characterize the attachment/detachment kinetics of the acto-myosin interaction in skinned skeletal fibers (20,21). To determine if Vi alters _k_att/_k_det we compared the chord stiffness of skinned cardiac trabeculae during maximal Ca2+ activation (pCa 4.5), without and with Vi, as described in Fig. 4. Trabeculae were stretched (0.15 %ML) at varying rates from 0.1 to 1500 %ML s−1. Chord stiffness was obtained in rigor to determine the maximum stiffness and stretch rate dependence of stiffness for strongly bound, noncycling cross-bridges (solid circles). Vi decreased chord stiffness compared to control (open circle; pCa 4.5 without Vi) at stretch rates above ∼10 %ML s−1. Below this rate chord stiffness increased slightly relative to control (Fig. 4 A). To illustrate the differing sensitivity of chord stiffness to Vi at low and high stretch rates the data in panel A were normalized to the maximum stiffness at high stretch rates at each [Vi] in Fig. 4 B. This emphasizes a peak or plateau in chord stiffness at slower stretch rates, that becomes more prominent as the [Vi] increases and the absolute magnitude of chord stiffness at high stretch rates decreases. Above 10 %ML s−1 the normalized stiffness-stretch rate dependence at all [Vi] was not different from maximally activated controls (no Vi). The dependence of chord stiffness on stretch rate is thought to be determined primarily by the apparent cross-bridge detachment rate (_k_det) (Brenner (20); Schoenberg (46)). Thus the shift of the stiffness-stretch rate profile in Fig. 4 B toward slower rates implies decreased _k_det for a population of cross-bridges with bound Vi and could be consistent with the apparent slow Vi dissociation rate evidenced by prolonged force recovery (Fig. 1). Although decreased stiffness at high stretch rates with Vi implies decreased cross-bridge/thin filament interaction, the data at low rates indicate that a significant fraction of cross-bridges with bound Vi might still interact with thin filaments, albeit in weak-binding states that contributed little to force and stiffness.

FIGURE 4.

FIGURE 4

Skinned trabeculae were stretched at constant amplitude (0.5 %ML) at varying rates and the resulting changes in stiffness were measured at various [Vi], as indicated in the inset. In A the results were compared to maximum Ca2+ activation (no Vi; ○) and rigor (•). Vi reduced stiffness at all rates of stretch above ∼10 %ML s−1, whereas below this rate stiffness increased. In A data are normalized to the maximum stiffness at high stretch rates in uninhibited controls. Chord stiffness in B is expressed relative to the maximum stiffness value at high rates of stretch for each [Vi]. The data in B emphasize the peak in chord stiffness at slower rates of stretch, implying the presence of a cross-bridge population with slowed attachment/detachment kinetics. The curves in panels A and B were obtained by nonlinear fitting of the data with Peak-Fit (SPSS, Chicago, IL).

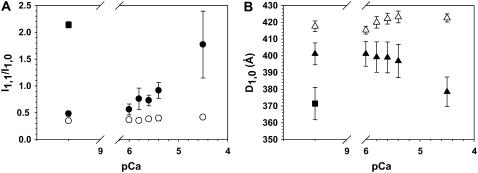
To determine if this was the case, we used low angle x-ray diffraction of activated skinned trabeculae to characterize Vi effects on cross-bridge/thin filament interaction more directly. Changes in the ratio of the 1,1 and 1,0 equatorial reflection intensities (_I_1,1/_I_1,0) during Ca2+ activation were measured in the presence (1.0 mM) and absence of Vi. Although it was not possible to measure force with our x-ray apparatus, data were obtained with exactly the same solutions and conditions used for force measurements and the trabeculae were in a small volume (∼0.5 ml) chamber for rapid solution changes (<1 s). Increased or decreased _I_1,1/_I_1,0 indicates a corresponding movement of cross-bridge mass toward or away from thin filaments, respectively. Trabeculae were maximally activated and then exposed to pCa 4.5 with 1.0 mM Vi and relaxed. Vi treated preparations were subsequently exposed to increasing [Ca2+] in the presence of 1.0 mM Vi. The [Ca2+] dependence of _I_1,1/_I_1,0 in controls and Vi treated trabeculae is shown in Fig. 5 A, along with corresponding changes in myofilament lattice spacing (_D_1,0) in Fig. 5 B. Without Vi (solid circle) _I_1,1/_I_1,0 increased nearly fourfold (n = 5 trabeculae) over the pCa range where force increased (see Fig. 8 A). In contrast, whereas _I_1,1/_I_1,0 was increased slightly (from 0.35 ± 0.02 to 0.42 ± 0.03; P < 0.05) from pCa 6.0 to pCa 4.5 with 1.0 mM Vi (open circle; n = 4 trabeculae)), it was greatly reduced compared to control over the same pCa range. Vi had no effect on the relaxed (pCa 9.2) equatorial ratio.

FIGURE 5.

FIGURE 5

The equatorial x-ray reflection intensity ratio (_I_1,1/_I_1,0; Fig. 5 A) and myofilament lattice spacing (_D_1,0; Fig. 5 B) was determined at various [Ca2+] from pCa 9.2 to 4.5 in the absence (solid symbols; n = 6 trabeculae) and presence (open symbols; n = 4 trabeculae) of 1.0 mM Vi. _I_1,1/_I_1,0 (A) and _D_1,0 (B) for rigor conditions (▪; n = 4) are included for comparison.

FIGURE 8.

FIGURE 8

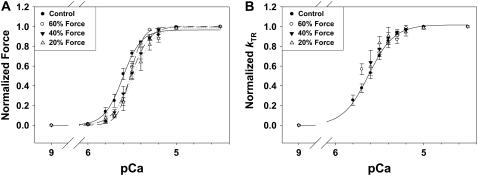
The Ca2+ dependence of force (A) and _k_TR (B) are shown at different [Vi]. Force in panel A and _k_TR in panel B are normalized to the maximum for each condition. Data were pooled from fibers that produced ∼60% (○; dashed line), ∼40% (▾; dashed-dot line), and ∼20% (▿; dotted line) of maximum Ca2+-activated force in control fibers. The force data in panel A were fit with the Hill equation and pCa50 and _n_H are included in Table 1, along with corresponding values of _F_max and maximal _k_TR. The Hill fit parameters for control _k_TR-pCa data in panel B were 5.62 ± 0.01 and 3.0 ± 0.14, for pCa50 and _n_H, respectively.

Interestingly, lattice spacing (_D_1,0; Fig. 5 B) decreased with increasing [Ca2+] in the absence of Vi, as observed in skinned skeletal fibers (22,23), whereas with Vi increasing [Ca2+] had no significant effect on _D_1,0 (Fig. 5 B). The observation that _D_1,0 decreased during Ca2+ activation of skinned cardiac muscle is important and indicates that initial relaxed lattice spacing may not be an accurate indicator of the spacing achieved during active contraction. Taken together these data show that force inhibition by Vi was associated with cross-bridge mass movement away from thin filaments and toward thick filaments, indicating decreased cross-bridge/thin filament interaction. Similar Vi effects on thick filament structure have been observed in frog skinned skeletal fibers (24).

Effects of ADP and Pi on force, _k_TR, and stiffness at maximal Ca2+ activation

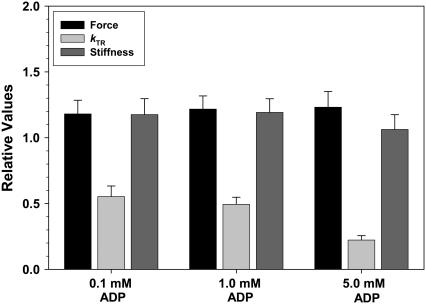
To support the idea that stiffness elevation at slow stretch rates with Vi reflected slowed _k_att/_k_det (Fig. 4), we measured chord stiffness when actomyosin cycle kinetics were altered by means other than Vi. To decrease cross-bridge cycling kinetics 0.1, 1.0, or 5 mM ADP was added to pCa 4.5 activating solutions (25,26), whereas increased [Pi] (30 mM) was used to increase cross-bridge kinetics, as shown for both skinned skeletal (27) and cardiac preparations (28,29). Addition of up to 5.0 mM ADP to bathing solutions increased _F_max and sinusoidal stiffness by ∼20%, and greatly reduced _k_TR, as shown in Fig. 6. Similar effects of elevated [ADP] on force and _k_TR were obtained in skinned skeletal fibers (25,30–33). Slowing of _k_TR by ADP has been attributed to reduction of _k_det (33–36); 30 mM Pi inhibited _F_max and maximal sinusoidal stiffness to 0.47 ± 0.15 and 0.49 ± 0.16 (n = 3 trabeculae) of control (no added Pi), respectively.

FIGURE 6.

FIGURE 6

The effects 0.1, 1.0, and 5.0 mM ADP on maximum Ca2+-activated force (black bars), _k_TR (light gray bar), and sinusoidal stiffness (dark gray bar) are illustrated. Data were obtained from six trabeculae. Values are expressed relative to those obtained with no added ADP.

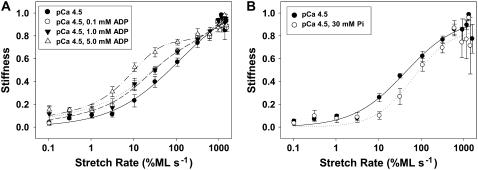
Chord stiffness versus stretch rate relations demonstrated that Vi (Fig. 4) acts on cross-bridge kinetics differently than does increased [ADP] or 30 mM Pi (Fig. 7, A and B, respectively). Data in Fig. 7 are expressed as a fraction of maximum obtained in each condition at the highest stretch rate and were obtained at 2.0 _μ_m initial SL. In Fig. 7 A increasing [ADP] increased stiffness at stretch rates between 10 and 100 %ML s−1, creating a plateau in the stiffness versus stretch rate relation when [ADP] was 5.0 mM. This range for elevated stiffness was ∼10–100 times faster than following Vi inhibition of force (Fig. 4). This cannot be attributed to rigor cross-bridges, as the activation solutions all contained 10 mM ATP (see Methods). The data in Fig. 7 indicate that with Vi enhancement of stiffness at very slow stretch rates (Fig. 4) likely indicates the presence of a process with significantly slower attachment-detachment kinetics than found in the presence of ADP. Importantly, 30 mM Pi shifted the entire chord-stiffness curve (Fig. 7 B) toward higher stretch rates and faster kinetics compared to controls (no added Pi). This is different than the effect of Vi (Fig. 4) and strongly suggests that Vi does not act as a functional Pi analog in terms of mechanical properties of cross-bridges.

FIGURE 7.

FIGURE 7

The influence of increasing [ADP] and 30 mM Pi on chord stiffness measurements is illustrated in panels A and B, respectively. Data were obtained from six trabeculae in A and three trabeculae in B. In panel A data were obtained at pCa 4.5 with 0.1 mM (○; heavy dashed line), 1.0 mM (▾; dotted line) and 5.0 mM (▵; dashed-dot-dot) ADP. Respective control measurements with no ADP or Pi added to solutions are shown in A and B (•; solid lines). Chord stiffness at each rate of stretch is normalized to the maximal level of stiffness at high rates of stretch for each condition. Initial SL was 2.0 _μ_m.

Effect of Vi on the Ca2+-activation dependence of _k_TR

The Ca2+ dependence of force and _k_TR at various [Vi] are shown in Fig. 8 A and B, respectively. Data (means ± SE) were normalized to _F_max or maximal _k_TR in controls with no Vi. Force in Fig. 8 A was fit with the Hill equation and the pCa50 and slope (_n_H) for each condition are included in Table 1. While Fig. 3 and Table 1 both contain similar data describing the effect of Vi on _F_max, the results in each were acquired from different sets of trabeculae. Inhibition by Vi to 60% of _F_max decreased pCa50 and had no significant effect on _n_H. Greater levels of force inhibition did not further decrease pCa50 or alter _n_H (Table 1). Like force, _k_TR was Ca2+ dependent (Fig. 8 B). Over the range of [Ca2+] where _k_TR was measured in the presence of Vi, inhibition of force had little effect on the Ca2+ sensitivity of _k_TR. However, it should be noted that at higher [Vi] and greater force inhibition, it was difficult to obtain reliable _k_TR values at low [Ca2+] and very low forces. For this reason only the control _k_TR-pCa data were fit with the Hill equation in Fig. 8 B.

TABLE 1.

[NaVi] _F_max ±SE _k_TRmax† ±SE
(mM) N (mN/mm2) %_F_max* ±SE _n_H ±SE pCa50 ±SE (s−1) %_k_TRmax* ±SE
0.00 10 29.8 5.6 1.00 0.00 5.5 0.6 5.62 0.03 21.7‡ 1.7 1.00 0.00
0.05 6 15.7 3.1 0.66 0.02 7.2 1.1 5.52 0.01 19.5 2.2 0.91 0.10
0.10 7 9.8 2.0 0.40 0.03 5.0 0.2 5.52 0.03 18.7 2.1 1.03 0.10
0.30 6 8.4 2.2 0.20 0.02 4.9 0.9 5.48 0.03 18.9 3.0 1.14 0.08

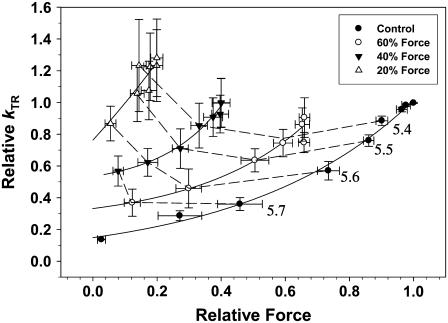
To illustrate the effect of Vi on the apparent thin filament activation level (force) the data in Fig. 8 were replotted in Fig. 9 as _k_TR versus force for varying [Vi]. Force is expressed relative to _F_max in the absence of Vi. At equivalent submaximal force levels, Vi increased _k_TR. However, similar force (to control) in the presence of Vi was obtained at higher levels of Ca2+, obscuring whether _k_TR was dependent more on Ca2+ or force level. To assist interpretation of the data the dashed lines in Fig. 9 indicate data obtained at the same [Ca2+]. This demonstrates that at the same submaximal [Ca2+], _k_TR increased when [Vi] was ≥0.3 mM and force was inhibited below 60% _F_max. The elevation of _k_TR at a constant [Ca2+] when force is inhibited by Vi, suggests that the rate of force development is not a simple function of either Ca2+ or the number of strongly binding cross-bridges in cardiac muscle. This will be discussed below in detail.

FIGURE 9.

FIGURE 9

The data in Fig. 8 are replotted as _k_TR versus isometric force (relative to pCa 4.5 in controls), to emphasize the activation dependence of _k_TR in skinned cardiac trabeculae at increasing levels of force inhibition with Vi. Data obtained at a given [Ca2+] is connected by dashed lines, with the pCa being given at the right.

DISCUSSION

We characterized the effects of force inhibition by Vi on cross-bridge binding to thin filaments and on force redevelopment kinetics (_k_TR) in skinned cardiac trabeculae from rats. Vi inhibited force to a greater extent than sinusoidal stiffness (Fig. 2), often used as an indicator of the number of strongly bound cross-bridges, and had a complex effect on the apparent attachment-detachment kinetics of cross-bridges, as determined with chord-stiffness measurements (Fig. 4). Chord-stiffness measurements in conjunction with data from x-ray diffraction (Fig. 5) indicate that at intermediate levels Vi inhibits force by establishing a separate population of weak-binding cross-bridges with very slow kinetics, while leaving a population of normal cycling cross-bridges. Other significant findings of this study were that whereas Vi inhibited maximal force (_F_max) and stiffness, maximal _k_TR actually increased at higher [Vi] (Figs. 3 A and 9). Furthermore, at submaximal Ca2+ activation Vi increased _k_TR (Fig. 9), opposite of what might be expected if _k_TR were dependent only on the level of steady-state force or [Ca2+]. These results are discussed in the context of the effects of Vi on: 1), the partition of cross-bridges between states that interact weakly or strongly with thin filaments (Fig. 4); 2), the effects of inhibiting strong cross-bridges on the Ca2+ sensitivity of force and _k_TR (Fig. 8); and finally, 3), mechanisms whereby Vi increased the rate of cross-bridge transition from weak- to strong-binding, force-producing states ((_k_TR; Fig. 9).

Effects of Vi on cross-bridge binding to cardiac thin filaments

Vi is a phosphate analog that binds to the myosin-S1 head and inhibits acto-myosin ATPase (37) and force (17). The M.ADP.Vi complex is an analog of the posthydrolysis M.ADP.Pi state that binds weakly to actin (17). Cross-bridges with bound Vi appear to be in the “closed” structural conformation (38,39) correlated with a posthydrolysis or preforce state (40,41). Vi dissociates slowly from either M.ADP.Vi or from A.M.ADP.Vi, as evidenced by: 1), an apparent lack of force recovery following prolonged exposure of Vi-treated fibers or trabeculae to relaxing solution without Vi; and 2), the slow force recovery when Vi-treated skeletal (17,18) or skinned cardiac trabeculae (Fig. 1) are exposed to activating Ca2+. The apparent slow dissociation of Vi, compared to Pi, prevents or greatly slows cross-bridge transition into force generating states. Thus, although Vi is a phosphate analog, its slow dissociation from myosin contrasts with the rapid kinetics of Pi exchange (42).

Our observation that sinusoidal stiffness was inhibited to a lesser extent than force by Vi (Fig. 2, A and B), indicates that the cross-bridge population shifts toward states that bind weakly (no force), but strongly enough to contribute to fiber stiffness (27). However, this interpretation of stiffness data must be tempered by at least two considerations. First, skinned cardiac trabeculae have unavoidable compliances from damage to the ends where T-clips are fastened and second, myofilament compliance can lead to an overestimation of fiber stiffness, particularly at low forces (43,44). On the other hand, the chord stiffness data in Fig. 4 appear to support the idea that in the presence of Vi during Ca2+ activation the cross-bridge population shifts away from active cycling toward stably bound states that have slow attachment/detachment kinetics and interact weakly with thin filaments. This idea is further supported by our observation that the equatorial x-ray reflection ratio (_I_1,1/_I_1,0; Fig. 5 A) is significantly reduced at maximal activating [Ca2+] by 1.0 mM Vi, indicating a reduction of both strong and weak cross-bridge/thin filament interaction.

Chord stiffness: implications for cross-bridge binding and kinetics

The relationship between chord stiffness and the rate of fiber stretch is sensitive to changes in attachment-detachment kinetics, with the overall kinetics being dominated by _k_det (_k_att ≫ _k_det) (20,45,46). This analysis assumes the _k_att controls the initial diffusion limited formation of the A.M.ATP or A.M.ADP.Pi collision complex and is thus fast. During a constant amplitude stretch at a given rate, the amount of stiffness measured will be directly determined by the fraction of time cross-bridges are bound to actin (_k_att/(_k_att + _k_det)). In the absence of Ca2+ weak, nonforce-producing cross-bridges bind to thin filaments with very fast kinetics and stiffness is only generated at rapid rates of stretch (21). In contrast, if _k_det is decreased relative to _k_att, as would occur during active contraction, cross-bridges will interact longer with actin during the stretch, leading to increased cross-bridge strain and shifting the stiffness versus stretch rate relation toward slower stretch rates, as seen with elevated [ADP] (Fig. 7).

Force inhibition by Vi had a complex effect on the stiffness-stretch rate relationship (Fig. 4, A and B). Increasing [Vi] inhibited stiffness at stretch rates above 10 %ML s−1, indicating a shift of cross-bridges from strong- to weak-binding states. In contrast, from 0.1 to 1 %ML s−1 stiffness was slightly increased (compared to controls), causing a broad elevation that reached a maximum at ∼1 %ML s−1. Elevation of chord stiffness at ∼1 %ML s−1 with increasing [Vi] (Fig. 4 B) is consistent with an increasing population of weak-binding (no or low force) cross-bridges in the AM.ADP.Vi state that are characterized by slow attachment-detachment kinetics. This contrasts with the effect of ADP or Pi (which also alters _k_att/_k_det), where chord stiffness increases over a different range of stretch rates (Fig. 7).

Elevated [ADP] increased _F_max and slowed _k_TR in cardiac trabeculae (Fig. 6). In skinned skeletal fibers increased force, decreased _k_TR and decreased unloaded shortening velocity with elevated [ADP] were attributed to a decreased cross-bridge/detachment rate (33–36). Likewise the enhancement of chord stiffness at slower stretch rates (Fig. 7 A) is consistent with decreased apparent _k_det of active cycling cross-bridges. For cycling cross-bridges under control conditions the amount of stiffness measured at the fastest attainable rates of stretch is limited by the rapid _k_det. If this were not true stiffness should become constant at the highest stretch rates (20,45,47). Thus, the relative constancy of stiffness from ∼100 to 1500 %ML s−1 in Fig. 7 A indicates that elevated ADP decreased _k_det, thereby prolonging strong cross-bridge binding and maximizing cross-bridge strain at much lower stretch rates. It should be noted that although both ADP and Vi elevated stiffness at slow rates of stretch during maximal Ca2+ activation, ADP enhanced strong cross-bridge binding and force (Fig. 6), whereas Vi decreased strong cross-bridge binding and force (Figs. 2 and 4). Thus, comparison of the chord stiffness data for Vi versus ADP demonstrates that slowed apparent cross-bridge cycling rates occur by different mechanisms. With ADP slowing comes from a buildup of cross-bridges in strongly bound states (due to reduced _k_det), whereas with Vi slowing of apparent attachment-detachment kinetics is correlated with reduced numbers of cross-bridges that participate in cross-bridge cycling and force generation.

In contrast to ADP (Fig. 7 A) the right shift of the chord stiffness versus stretch rate relation with 30 mM Pi (Fig. 7 B) is consistent with faster cross-bridge cycling, evidenced by increased _k_TR in skeletal (27) and cardiac muscle (29), and rapid reduction of strong cross-bridge binding by photo-released Pi in skinned skeletal fibers (48) and cardiac myocytes (29). Furthermore the entire curve in Fig. 6 was shifted toward higher stretch rates with elevated Pi, implying that apparent _k_det increased in the majority of the cycling cross-bridge population. These observations are consistent with the idea that Pi exchange on myosin is rapid (42), unlike Vi. Furthermore, the shift in the stiffness/rate profile to faster rates with increased [Pi] (Fig. 7 B) contrasts sharply with the corresponding effects of Vi (Fig. 4), a phosphate analog. Thus, unlike Vi, there is no evidence for Pi partitioning cross-bridges into noncycling and cyling populations.

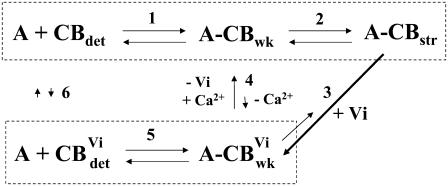
Although speculative, the following simple schematic provides a framework within which the effects of Vi on steady-state force and stiffness in cardiac muscle can be interpreted:

Step 1 indicates initial cross-bridge binding in the “weak” state that is obligatory (49) for cross-bridge isomerization into force generating states in the presence of Ca2+ (step 2). The kinetics of step 1 are thought to be rapid, as indicated by increasing chord stiffness at high rates of stretch in relaxed skeletal (21) and cardiac muscle (16). When Vi binds to cross-bridges in activating solutions, there is a transition to a weak-binding Vi bound state (thick arrow; step 3) that is in dynamic equilibrium with detachment (step 5). Strong force inhibition by Vi in the presence of Ca2+ (step 3) implies that the transition of weak cross-bridges with bound Vi to strong binding is comparatively small (thin arrow; step 3). When Vi is removed in the presence of Ca2+, cross-bridges can slowly exchange Pi for Vi and transition toward strong binding states, as evidenced by a prolonged recovery of force (Fig. 1). This could occur in the presence of Ca2+ by either slow exchange of Vi for Pi (step 4) or by slow dissociation of Vi from AM.ADP.Vi to produce AM.ADP, which transitions directly into strong binding (thin arrow; step 3). In either case the population of strong binding cross-bridges increases during recovery from inhibition.

There are two observations that suggest little or no exchange of Pi for Vi between the cross-bridge populations with either Vi or Pi bound (dashed boxes) when Vi is present in either activating (step 4) or relaxing (step 4 or 6) solutions. First, exposure of fibers to Vi in relaxing solutions, before Ca2+ activation without Vi, does not inhibit subsequent Ca2+ activation of force. Second, once force is inhibited by Vi in activating solutions, long exposures to relaxing solution without Vi does not reverse inhibition (see Fig. 1).

One consequence of this scheme is that with Vi two populations of weak-binding cross-bridges may be established, those with either Pi or Vi bound. The weak-binding cross-bridges with Pi would cycle with normal rapid attachment/detachment kinetics and in the presence of Ca2+ transition into strong-binding states, whereas those with bound Vi would be “locked” into a weak state with slow apparent _k_att/_k_det. The slow recovery of force in inhibited fibers following activation without Vi suggests that Vi dissociation from cross-bridges is slow. If true, detachment of cross-bridges with bound Vi from actin (_k_det) may be slower than cross-bridges with Pi bound, as indicated by comparison of Figs. 4 and 7 B. The presence of a “hump” in the stiffness-stretch rate relation (Fig. 4) is consistent with at least two stable weak binding cross-bridge populations, with little exchange between them (steps 4 and 6), as long as Vi is present. If exchange between these two states was rapid one might expect a shift of the entire curve toward faster stretch rates, as found for elevated Pi (Fig. 7 B), rather than the appearance of a distinct peak or plateau at slow stretch rates. Therefore, the data are consistent with the presence of a distinct population of weakly binding cross-bridges with slowed attachment/detachment kinetics, along with a population of normally cycling cross-bridges, indicated by the similar stretch rate dependence of stiffness at faster rates of stretch, with and without Vi (Fig. 4 B). This interpretation is consistent with observations that whereas elevated Pi inhibits force, but not unloaded shortening velocity in skinned skeletal fibers (50), Vi inhibits both (18). This, along with the chord stiffness data in Fig. 4, implies that cross-bridges with bound Vi interact with thin filaments long enough to impose an internal load on shortening.

Figure .

Figure

The effects of Vi on _k_TR

Force inhibition by Vi was associated with enhanced _k_TR at all submaximal force levels (Fig. 8 B), but had little effect on the Ca2+ sensitivity of _k_TR (Fig. 7 B). A similar enhancement of contractile kinetics in cardiac muscle was described by Herzig et al. (51). When Vi inhibited force, force redevelopment kinetics following a rapid stretch and the ATPase/force ratio in cardiac muscle was increased. Maximal _k_TR in skeletal muscle is thought to be determined primarily by the intrinsic rate of acto-myosin cycling (20,52,53). However, we (54), and others (55), have recently demonstrated that maximal _k_TR in cardiac muscle is also dependent on thin filament activation state; _k_TR is Ca2+ dependent in striated muscle, exhibiting a strong apparent cooperativity when plotted against force. Significant evidence (reviewed in Gordon et al. (1) and Regnier et al. (54)) suggests this Ca2+ regulation occurs via modulation of thin filament state, which regulates cross-bridge transitions from weak to strong binding, force bearing states, and, perhaps, the rate of cross-bridge detachment (56,57).

The contributions of thin filament activation by Ca2+ and cross-bridges (weak to strong transitions) to _k_TR are emphasized in Fig. 9. When strong cross-bridge binding and force were inhibited by Vi _k_TR was faster at a given level of submaximal force. However, force in Fig. 9 is expressed relative to maximal (pCa 4.5) in controls (no Vi). Because increasing [Vi] decreased force at a given [Ca2+], a higher [Ca2+] was required to achieve the same relative force. Thus faster _k_TR with elevated [Vi] (at the same relative force level; Fig. 9) was associated with increased [Ca2+]. This makes it difficult to distinguish whether _k_TR was increased by Vi or by elevated [Ca2+] and Ca2+ binding to thin filaments. However, when data are compared at the same submaximal [Ca2+] (dashed lines; Fig. 9), force inhibition below 60% _F_max by Vi increased _k_TR. Thus at a given [Ca2+] elevated _k_TR in the presence of Vi was associated with reduced cross-bridge binding and a decreased cross-bridge population available for recruitment (Fig. 4). These observations indicate that _k_TR dependence on thin filament activation is determined by both Ca2+ binding to troponin and the availability of cross-bridges for recruitment to strong-binding states. Furthermore the increase of _k_TR at a given submaximal [Ca2+] with increasing [Vi] (dashed lines; Fig. 9) could be underestimated. While bathing [Ca2+] was the same, force inhibition probably decreased the amount of Ca2+ bound to thin filaments. This is because strong cross-bridge binding has been shown to enhance Ca2+ binding to troponin in cardiac muscle (5,6). Consequently, at higher [Vi] less Ca2+ could be bound to thin filaments at the same bathing solution [Ca2+]. This implies that if _k_TR could be compared at the same submaximal level of Ca2+ binding to troponin, _k_TR would increase even more at a given [Vi].

Although our results imply that the apparent activation dependence of _k_TR in cardiac muscle reflects the effects of both Ca2+ binding and cooperative activation of cardiac thin filaments by strongly bound cross-bridges, an alternative explanation for the effects of Vi on _k_TR is possible. For example, elevation of _k_TR by Vi could be explained if cross-bridges in the weak-binding AM.ADP.Vi state were capable of activating cardiac thin filaments. If true, cross-bridges with bound Vi could elevate thin filament activation similar to NEM-S1 (55), although NEM-S1 increased the Ca2+ sensitivity of force, whereas Vi decreases it (Fig. 7 A; Table 1). However, several arguments can be made against this explanation. First, the absolute magnitude of the stiffness at ∼1 %ML s−1 is only ∼5% of the maximum stiffness at the fastest stretches (Fig. 4 A), implying a corresponding proportion of bound cross-bridges in the AM.ADP.Vi state (assuming that cross-bridges in all states have approximately the same unitary stiffness). The corresponding decrease in equatorial reflection ratio at full Ca2+ activation (Fig. 5 A) is also consistent, in conjunction with chord-stiffness measurements (Fig. 4), with Vi causing a significant reduction in cross-bridge/thin filament interaction. Thus it is difficult to imagine how a small population of weak-binding cross-bridges could cause significant thin filament activation. Furthermore, if cross-bridges with bound Vi attached to cardiac thin filaments in a “rigor-like” state, and were able to activate thin filaments, then inspection of the rigor data in Fig. 4 A suggests that stiffness should be elevated at all stretch rates, unlike the relative elevation of stiffness at ∼1 %ML s−1. Finally, Fig. 4 A indicates that the absolute amplitude of stiffness at all stretch rates decreased above 0.02 mM Vi. If the “hump” in stiffness at low stretch rates is attributed to cross-bridges in the AM.ADP.Vi state, it is difficult to attribute an increase of apparent activation at higher [Vi] (elevated submaximal _k_TR; Fig. 9) to a decreasing population of cross-bridges with bound Vi.

Increased _k_TR when force and the fraction of normal cycling cross-bridges is reduced by Vi can be understood in the context of a model of cardiac contractile activation proposed by Campbell (58) and Razomova et al. (59). In this model the activation dependence of _k_TR reflects not only the intrinsic kinetics of the acto-myosin interaction, but also cooperative activation of thin filaments during recruitment of strong-binding cross-bridges. This idea is supported by structural studies indicating that cycling strong cross-bridges stabilize the “open” thin filament state (2). The Campbell/Razumova model suggests that _k_TR is slowed at submaximal Ca2+ activation because under this condition the available cross-bridge pool for recruitment is large. As recruitment proceeds activation by cross-bridges incrementally increases and the approach to the final steady force level is slowed (58). Steady force at a given [Ca2+] is finally achieved when strong cross-bridge recruitment is balanced by cross-bridge transition to weak-binding states. In contrast, at higher [Ca2+] and greater strong cross-bridge binding to thin filaments, the pool of cycling cross-bridges available for recruitment is reduced, along with the subsequent net effect of any cross-bridge recruitment on thin filament state. Thus interventions that reduce the size of the cross-bridge pool available for recruitment, such as inhibition of cross-bridge binding by Vi (Fig. 4), should reduce the slowing effect of cross-bridge recruitment on _k_TR and thereby cause _k_TR to become faster at submaximal Ca2+ activation, as we find (Fig. 9). In fact, Fig. 2 A indicates that with maximal force inhibition at 1.0 mM Vi _k_TR increased, suggesting that even at saturating [Ca2+] cross-bridge recruitment contributes to activation of cardiac thin filaments. This is consistent with the idea that at saturating [Ca2+] cardiac thin filaments may not be fully activated (54). Thus the effects of Vi on force and _k_TR at all levels of Ca2+ activation (Fig. 9) are consistent with the Campbell/Razumova model (58,59). The importance of cross-bridge recruitment in setting the level of thin filament activation and the kinetics of force development are further supported by recent observations that “stretch activation” in single cardiac myocytes was significantly reduced and force development kinetics elevated when thin filaments were activated with NEM-S1 (60).

Acknowledgments

The authors thank Drs. Franklin Fuchs and Albert M. Gordon for helpful comments on the manuscript and Mr. Gary Melvin (National Institute of Arthritis and Musculoskeletal and Skin Diseases (NIAMS), National Institutes of Health) for his technical and experimental support. We also thank the staff at beamline X27C at Brookhaven National Laboratories for their expert help.

This work was supported by NIH HL 67071 (D.A.M.) and NIH HL61683 (M.R.). This research was also supported in part by the Intramural Research Program of the NIAMS of the National Institutes of Health (L.Y. and S.X.).

References