A constant size extension drives bacterial cell size homeostasis (original) (raw)

. Author manuscript; available in PMC: 2015 Dec 4.

Abstract

Cell size control is an intrinsic feature of the cell cycle. In bacteria, cell growth and division are thought to be coupled through a cell size threshold. Here, we provide direct experimental evidence disproving the critical size paradigm. Instead, we show through single-cell microscopy and modeling that the evolutionarily distant bacteria Escherichia coli and Caulobacter crescentus achieve cell size homeostasis by growing on average the same amount between divisions, irrespective of cell length at birth. This simple mechanism provides a remarkably robust cell size control without the need of being precise, abating size deviations exponentially within a few generations. This size homeostasis mechanism is broadly applicable for symmetric and asymmetric divisions as well as for different growth rates. Furthermore, our data suggest that constant size extension is implemented at or close to division. Altogether, our findings provide fundamentally distinct governing principles for cell size and cell cycle control in bacteria.

Introduction

Cell size control, a universal property of all organisms, reflects the balance between growth and division. Mechanisms must be in place to ensure that cells narrowly distribute around a characteristic size for a given cell type, species and growth condition. This is especially important for exponentially growing cells. Exponential growth implies that growth is proportional to cell size such that short cells grow slower than long cells in absolute growth rate. Thus, if no compensation occurs, any deviations from the mean size will increase cell size variability in the population at each generation. The very existence of a stable cell size distribution indicates the presence of intrinsic mechanisms that reduce cell size fluctuations.

Most cells from bacteria to yeast to mammalian cells are thought to regulate their size and cell cycle through critical size thresholds (Turner et al., 2012). In the critical size model, cells commit to division upon reaching a size threshold. Thus, all cells divide at about the same size whether they are born shorter or longer than the mean, compensating for their initial size deviation. The size threshold, or ‘sizer’, can be applied to a cell cycle event other than division, with completion of this earlier event licensing cell division to occur after a constant amount of time, or ‘timer’, has elapsed. For example, the yeast Saccharomyces cerevisiae and Schizosaccharomyces pombe display a size threshold at the G1-S transition and mitosis, respectively (Fantes, 1977; Johnston et al., 1977; Sveiczer et al., 1996). In the bacterial field, a ‘sizer + timer’ model gained momentum with seminal population studies in Escherichia coli and Salmonella typhimurium. A size threshold at the initiation of DNA replication was inferred from calculations showing that on average, DNA replication initiates at a constant cell mass under different growth rate conditions (Donachie, 1968). Although disputed (Bates and Kleckner, 2005; Boye and Nordstrom, 2003; Wold et al., 1994), a coupling of cell division to DNA replication through a fixed timer was suggested from experiments showing that the timing between DNA replication and cell division remains constant across different growth rates (Cooper and Helmstetter, 1968; Schaechter et al., 1958; Schaechter et al., 1962). These findings observed at the population level were then assumed to be applicable to individual cells.

Cell size homeostasis could, at least in theory, be achieved through mechanisms that do not involve the licensing of division upon attainment of a certain size. These alternative mechanisms include a molecular clock, a simple timer, the addition of a constant cell volume, transition probability, or a concerted ‘sloppy’ sizer and timer (Fantes and Nurse, 1981; Osella et al., 2014). For example, based on mathematical modeling, Voorn and Koppes first (1998), and Amir later (2014) argued that addition of a constant volume at each generation can describe the experimental shape of bacterial cell size distributions as well as population-derived bulk correlations (the positive correlation in size between mothers and daughters and the negative correlation between cell cycle time and size at birth). However, these statistical features have alternative explanations (Hosoda et al., 2011; Osella et al., 2014) and can be described by sizer-based homeostasis mechanisms (Koch and Schaechter, 1962; Koppes et al., 1980; Robert et al., 2014; Turner et al., 2012). The concept of sizer-based control has prevailed in the bacterial literature, and, apart from the exception of Mycobacterium (Santi et al., 2013), still persists today as an underlying assumption in virtually all bacterial cell size and cell cycle studies.

Importantly, beyond their associated caveats, all bacterial cell size homeostasis models—including the prevalent sizer-based models—lack direct experimental evidence. A direct examination of an intrinsic cell size mechanism requires the ability to track a large number of individual cells. Cell tracking must occur in the absence of environmentally-induced cell size fluctuations. This is important because E. coli and other bacteria traditionally used for cell size studies change their average size in response to nutrient availability and cell density (Akerlund et al., 1995; Schaechter et al., 1958). Finally, cell size must be measured with high precision and at high temporal resolution, preferably over multiple cell cycles.

Another overlooked aspect of bacterial cell size homeostasis is the role of division site placement. Most bacterial cell size studies — whether experimental or theoretical — have focused on symmetrically dividing bacteria, even though asymmetric divisions are well represented in the bacterial world. For example, the large class of α-proteobacteria appears to be dominated by asymmetrically dividing bacterial species. The best studied α-proteobacterium is Caulobacter crescentus, which divides asymmetrically to produce two daughter cells of unequal sizes, known as the stalked and swarmer cells (Figure 1A).

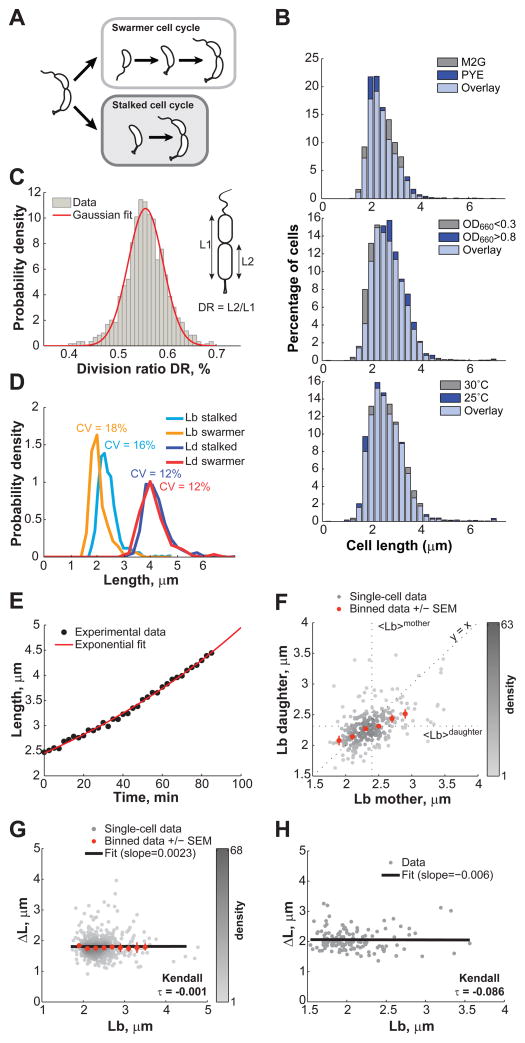
Figure 1. Cell length control in C. crescentus.

(A) Schematic of the dimorphic cell cycle of C. crescentus. Each division generates two different progeny: the smaller swarmer cell and the longer stalked cell. The swarmer cell is motile thanks to a polar flagellum until the cell transitions to a stalked cell. (B) Distribution of C. crescentus CB15N lengths under different environmental conditions. Cells were grown in M2G at 30°C and imaged on 1% agarose pads at an OD660nm < 0.3 except if stated otherwise. (C) Histogram representing the distribution of the division ratio DR for C. crescentus CB15N cells (n = 706) grown in M2G medium and imaged on 0.3% agarose pads. (D) Distribution of cell length at birth Lb, and at division Ld for stalked cells (n = 565) and swarmer cells (n = 141) grown in M2G medium at 30°C and imaged at OD660nm < 0.3 on 0.3% agarose pads. The coefficient of variation (SD/mean) for each distribution is shown. (E) Representative growth curve of a single stalked cell (black circles) grown in M2G medium at 30°C on a 0.3% agar pad. The red line is the best fit of the data with an exponential function. (F) Partial inheritance of Lb from one generation to the next (n = 457 stalked cells). The vertical and horizontal dotted lines indicate the mean length at birth for mother and daughter cells. The line y = x is also plotted for comparison purposes. (G) Dependence of the elongation over a cell cycle (ΔL) on Lb for stalked cells. Grey dots represent single-cell data while orange dots represent the average of binned data ± SEM (standard error of the mean). The shade of grey represents the density of points in a given area of the graph. The black line represents the linear fit to the single-cell data. (H) Dependence of ΔL on Lb for swarmer cells. There were not enough cells (n = 141) to bin the data. See also Figure S5, S7 and Movie S1.

In this study, we performed high-precision single-cell time-lapse microscopy studies on C. crescentus and E. coli to uncover the intrinsic principles of bacterial cell size homeostasis for both symmetric and asymmetric divisions.

Results and discussion

C. crescentus does not appear to vary its cell length in response to changes in nutrient availability, cell density or temperature

In this study, we focused on cell length as this is the cell size dimension that changes during the cell cycle. Cell length in bacteria is generally thought to be sensitive to environmental conditions. For example, E. coli and other bacteria are known to modulate their average length in response to nutrient availability and cell density (Akerlund et al., 1995; Schaechter et al., 1958). Using high-precision image analysis software (Sliusarenko et al., 2011), we found that while the cell width slightly varies (Harris et al., 2014), the length of asymmetrically dividing C. crescentus appears insensitive to environmental fluctuations. There was no discernable difference in cell length distributions between C. crescentus populations grown in nutrient-poor (M2G) or nutrient-rich (PYE) medium (Figure 1B), despite significant differences in growth rates, with doubling times of 146 ± 5 min in M2G (mean ± SD, n = 2 experiments) and 96 ± 1 min in PYE (n = 2). Varying cell density (OD660nm < 0.3 vs. > 0.8) or temperature (25°C vs. 30°C) also had little effect on cell length distributions (Figure 1B). These distributions were reproducible from day to day (data not shown). Thus, C. crescentus populations exhibited the same cell length distributions under all growth conditions tested, indicating robust cell length homeostasis. This allowed us to examine the intrinsic properties of cell length control, without concern of interference from environmental fluctuations.

C. crescentus controls its cell length

Studying cell length control requires precise measurements of cell length over at least one full cell cycle. Obtaining swarmer cells in G1 phase is relatively easy (Evinger and Agabian, 1979). However, the synchronization technique does not distinguish between the ‘young’ swarmer cells that are fresh from division from the ‘older’ swarmer cells that are about to become stalked cells. Furthermore, the technique, like most cell cycle synchronization methods, perturbs cellular metabolism. Therefore, we performed time-lapse phase contrast microscopy of asynchronous populations and monitored growth and division (see Experimental procedures). Analysis showed that when cells were spotted on regular 1% agarose pads containing M2G medium, the average cell length became significantly shorter (~ 10%) even after a single cell cycle. We reasoned that this cell shortening was likely caused by physical constraints due to immobilization on the solid agarose (1%) substrate. To reduce this potential ‘sticky’ problem, we spotted cells on soft agarose (0.3%) pads. In this more aqueous environment, cells were more loosely immobilized, allowing newborn swarmer cells to swim away immediately after their physical separation from the stalked cell sibling following division (Movie S1). This soft-agarose microscopy set-up allowed us to track stalked cells over time and to measure their length from birth (Lb) to division (Ld). In this environment, the cell lengths remained similar between divisions, with cell length at birth Lb = 2.43 ± 0.39 μm (mean ± SD, n = 252 cells) after the first division vs. Lb = 2.42 ± 0.40 μm (n = 193 cells) after the second division. Since swarmer cells occasionally became immobilized on the soft-agarose surface after a short swim (Movie S1), we also obtained measurements for swarmer cells, although many fewer (see Experimental procedures).

As expected (Terrana and Newton, 1975), division was asymmetric, with a division ratio DR (length between the stalked pole and the division site divided by the total length) of 0.56 ± 0.04 (n = 706 cells) (Figure 1C). The populations of newborn stalked and swarmer cells were characterized by narrow distributions of cell length at birth (Figure 1D). Both cell types had a very similar relative variability in length as measured by the coefficients of variation (CV, standard deviation/mean) of 16% and 18% for stalked and swarmer cells, respectively. Despite the shift in average length at birth, swarmer and stalked cells displayed similar distributions of cell lengths at division, indicating that swarmer cells must grow more than stalked cells to compensate for their shorter size at birth. The cell length distributions at division were narrow with a CV of about 12% (Figure 1D). This value is comparable to the CV determined for Saccharomyces cerevisiae at budding (CV = 17%) and Schizosaccharomyces pombe at fission (CV = 6%) (Di Talia et al., 2007; Lord and Wheals, 1981; Sveiczer et al., 1996), both of which are known to display cell size regulation.

Cell size compensation is partial over a single generation

Further analysis was primarily done on the stalked progeny given their higher sample size. Their cell elongation was consistent with exponential growth (Figure 1E), as reported previously (Siegal-Gaskins and Crosson, 2008). Exponential growth implies that a cell size compensation mechanism must be at work to maintain the narrow cell length distributions we observed. We indeed found that stalked cells born shorter than the population average produced stalked cells that were comparatively longer than their mothers (Lb of daughter > Lb of mother) (Figure 1F). The reverse was true for cells born longer than the mean; their progeny were comparatively shorter. However, the compensation was only partial (Figure 1F). This was surprising because a sizer-based model (with or without timer) implies that all cells shorter than the critical size grow until they reach their size threshold. As a result, there should not be any correlation in cell length between mothers and daughters for cells born shorter than the critical size. In other words, the ‘short’ phenotype is not an inheritable feature when a critical size mechanism is in place, unlike what we observed.

C. crescentus cells elongate by a constant amount on average, irrespective of cell length at birth

Another key characteristic of any sizer-based model is that cells born smaller than the mean size grow on average more before dividing than cells born longer. Thereby, in a sizer model, cell extension during the cell cycle (Δ_L_ = Ld_−_Lb) displays a strong negative correlation with the cell length at birth (Lb) for cells born shorter than the critical size (Fantes, 1977; Sveiczer et al., 1996). Strikingly, we found no significant correlation (slope ~ 0, Kendall τ = −0.001) between Δ_L_ and Lb for stalked cells (n = 565, Figure 1G). This seemed to be also true for the swarmer progeny, despite lower statistics (n = 141, Figure 1H). These data suggest that C. crescentus cells do not sense a certain size to regulate their length. Instead, they simply elongate the same amount on average (Δ_L_ = 1.81 ± 0.36 μm and 2.06 ± 0.35 μm for stalked and swarmer progeny, respectively) before dividing, regardless of their size at birth.

E. coli does not sense a cell size threshold to control its length

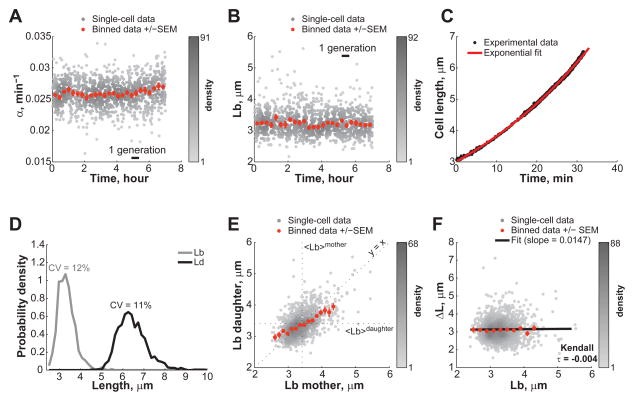
The surprising lack of cell size threshold in C. crescentus prompted us to revisit the critical size paradigm in E. coli, which had mostly been inferred from population studies under fast-growing conditions (Cooper, 1991; Cooper and Helmstetter, 1968; Donachie, 1968). Since the size of E. coli is sensitive to changes in nutrient availability or cell density, it was crucial to maintain constant growth conditions during measurements. For this, we used a microfluidic device (Ullman et al., 2013) that allowed us to track hundreds of E. coli BW25113 cells at the high temporal resolution of 5 seconds for hours (Figure S1 and Movie S2). We used fast-growth conditions (LB rich medium at 30°C) that resulted in a cell cycle length of 27 ± 5 min (mean ± SD, n = 1,305 cells). We verified that the growth rate and the average cell length at birth remained constant through the entire 7-h experiment (Figure 2A, B), indicating steady-state conditions. We also verified that the position of the cells in the microfluidic chamber had no influence on these parameters (Figure S1B). Cell elongation at the single-cell level was well approximated with an exponential function (Figure 2C), consistent with exponential growth.

Figure 2. Steady-state growth of E. coli BW25113 cells in microfluidic chambers.

E. coli BW25113 cells (n = 1,305) were grown in microfluidic chambers at 30°C in nutrient-rich LB medium. (A) Relative growth rate α over the course of the >7h-long microfluidic experiment. Grey dots represent single-cell data while orange dots represent the average of binned data ± SEM. (B) Same as panel A, except that Lb was plotted instead of α. (C) Representative growth curve of a single cell (black circles). Length was measured every 5 sec. The red line is the best fit of the data with an exponential function. (D) Distribution of Lb, and Ld. (E) Partial inheritance of Lb from one generation to the next. (F) Dependence of ΔL on Lb. The black line represents the linear fit to the single-cell data. See also Figures S1, S2, S5, S7 and Movie S2.

Cell lengths at birth and division were narrowly distributed with low CV of 12% and 11% (Figure 2D), respectively, consistent with previous reports (Koppes et al., 1980; Wakamoto et al., 2005). Strikingly, E. coli, even under fast-growing conditions, behaved similarly to C. crescentus in many respects. First, cells born shorter or longer than the mean only displayed partial cell size compensation over a single cell cycle (Figure 2E). Second, there was no correlation between the amount of elongation over a cell cycle and the length of cells at birth (Figure 2F). E. coli cells grew, on average, the same length (Δ_L_ = 3.23 ± 0.60 μm, mean ± SD, n = 1,305 cells) before dividing, independent of their initial size. These results demonstrate a fundamental conflict with the predictions of a sizer-based mechanism.

By analyzing published microfluidic data (Wang et al., 2010) (see Experimental procedures), we found that Δ_L_ is also independent of Lb for E. coli strains MG1655 and B/r growing at 37°C in 1-μm wide linear chambers (Figure S2), suggesting that our observations are independent from the strain, the microfluidic chamber geometry and the temperature.

A constant cell elongation per cell cycle results in cell size homeostasis

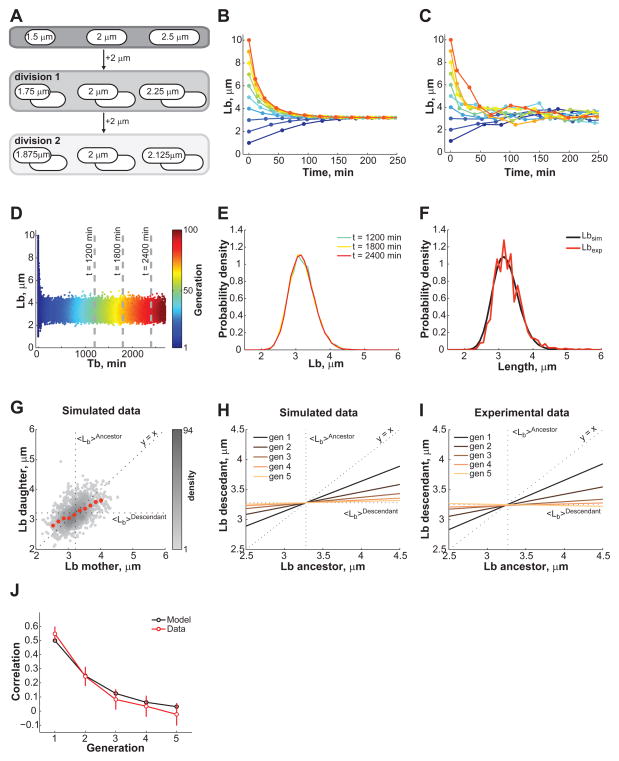
How can cells control their size in the absence of a sizer mechanism? Our data show that while there is significant fluctuations in Δ_L_ values, cells elongate, on average, a constant amount before dividing, irrespective of their length at birth (Figure 1G, H, Figure 2F, and Figure S2). A constant elongation — or the addition of a volume increment — can, at least theoretically, lead to cell size homeostasis (Amir, 2014; Voorn and Koppes, 1998). Figure 3A shows schematically how a constant length extension followed by a symmetric division can compensate for cell size fluctuations within a few generations. Mathematically (see SI, Eq. 3), cell lengths at birth that deviate from the mean converge exponentially over generations toward the constant elongation value in the absence of noise (Figure 3B). This assumes that all cells extend by the exact same increment Δ_L_, divide precisely in half, and grow at an identical relative rate α. In reality, these parameters fluctuate around an average value. When the experimental variability in Δ_L_, DR and α was considered in our mathematical model, stochastic simulations (see SI) showed that virtual newborn cells of varying initial lengths (1 to 10 μm) converge to the expected steady-state distribution of Lb within 2–4 divisions (Figure 3C). After that, Lb fluctuates around the average value (Figure 3D) and the population as a whole reaches a steady-state regime in which the Lb distribution remains stable over time (Figure 3E). Thus, the constant extension mechanism does not need to be precise to be robust.

Figure 3. Cell size control by a constant extension model.

(A) Schematic showing how a constant elongation allows cells of below- and above-average length to recover over time and generations. (B) Analytical dependence of Lb on time for 10 cells with Lb ranging from 1 to 10 μm. The time between data points represents the cell cycle (generation) time for that particular cell. See Table S1 for input parameter values. (C) Same as panel B except that the experimentally observed fluctuations around the DR, α and ΔL mean values were added to the simulation. (D) Evolution of Lb for 500 simulated cells with initially wide distribution of lengths. (E) Plot showing the distribution of Lb at the three time points indicated by the grey dashed lines in panel D. All cells present at the indicated times were considered to build the Lb distributions. (F) Plots showing the Lb distributions obtained from experiment and simulation (see Table S1 for input parameter values). (G) Plot showing the dependence in Lb between mother and daughter cells. The data were obtained from a stochastic simulation of the constant extension model using the same number of cells (n = 1,305) as in the experiment shown in Figure 2. (H) Degree of inheritance of Lb over 1 to 5 generations in simulations. Each line represents the best linear fit to the single-cell data of Lb for an ancestor and its descendant from the first to fifth generation. (I) Same plot as in panel H except that the data were derived from the experiment for E. coli LB experiment. (J) Evolution of the correlation between Lb from ancestors to descendants over generation expected from the model (black) or observed experimentally (red). The correlation was based on linear regressions of single-cell data. The error bars represent the 95% confidence interval around the slope value. See also Figure S3 and S5.

Remarkably, the steady-state distribution of Lb obtained from the simulations almost perfectly overlapped with the experimental distribution (Figure 3F), providing further support for the constant extension model. The model also quantitatively predicts the cell size compensation profile after one generation (Figure 3G compared to Figure 2E) as well as over subsequent generations (Figure 3H to compare with 3I). Since we were able to track cell lineages over several generations in our E. coli microfluidic experiments, we also showed that the correlation in Lb between ancestors and descendants drops with the number of generations (Figure 3J), following an exponential decay consistent with the constant extension model (see SI, Eq. 3). Thus, the model accurately predicts the degree of correlation in Lb between ancestors and descendants.

The constant extension model works equally well for asymmetric divisions. Using the experimental Δ_L_ and DR values for the C. crescentus dataset, simulations accurately reproduced the experimental Lb distribution of both stalked and swarmer daughter cells (Figure S3A). For symmetrically-dividing bacteria (average division ratio <DR_> = 0.5), the average length at birth (<_Lb_>) equals the average elongation (<Δ_L>), as shown for E. coli (Figure S3B). For asymmetrically-dividing bacteria, this is not the case (Figure S3C). <Δ_L_> of the longer progeny will correspond to <_Lb_> of the smaller one and vice versa (see SI, Eq. 2). For example, the average length extension of C. crescentus stalked cells is, within the measurement error, equal to the length of swarmer cells at birth (Figure S3C).

Precision in cell length at birth is dictated by the division ratio and the length extension between divisions

Just as the average Lb value is determined by the average Δ_L_ and DR values, deviations from this targeted size — which is reflected by the CV of the Lb distribution — will be dictated by the precision of both the constant extension mechanism and the positioning of the division machinery. Note that although the average Δ_L_ is equal to the average Lb for symmetrically dividing cells, variations in Δ_L_ and Lb can be different (Figure S3B). The constant extension model (see SI, Eqs. 14 and 15) quantitatively predicts how the CV of Lb depends on the CV of Δ_L_ and DR (Figure S3D, E). We found that the predicted CV values of Lb are in excellent agreement with the experimental values (Figure S3D, E).

Cell cycle time increases with shorter cell length at birth

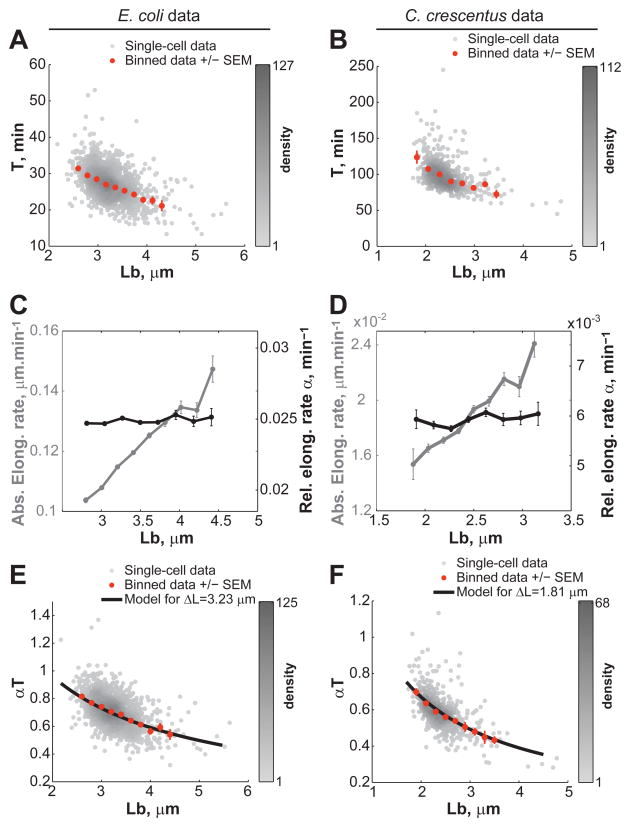
How do cells elongate by the same amount on average? Is it by modulating their cell cycle time T or by changing their relative elongation rate α? We found that for both the E. coli and C. crescentus datasets, T decreases as Lb increases (Figure 4A, B) while α remains fairly constant (Figure 4C, D), as previously reported for E. coli (Osella et al., 2014). Note that the relative elongation rate α (min−1) corresponds to the relative length increase over time, not to be confused with the absolute elongation rate (μm min−1), which is the absolute increase of cell length over a period of time. By virtue of their exponential growth, a constant relative elongation rate implies that the absolute elongation rate averaged over the cell cycle will increase with increasing Lb, which is what we observed (Figure 4C, D).

Figure 4. Cells correct their length at birth by modulating their cell cycle time and not their relative growth rate.

(A) Dependence of the cell cycle time T on Lb for E. coli grown in LB medium (n = 1,305 cells). (B) Same as panel A but for C. crescentus stalked cells grown in M2G medium (n = 565 cells). (C) Dependence of the absolute (grey) and relative (black) elongation rate α on Lb for E. coli. (D) Same as panel C but for C. crescentus. (E) Dependence of the normalized cell cycle time αT on Lb for E. coli. The black line represents the expected average αT from the constant extension model as described by the equation αT = ln(1+Δ_L_/Lb). The black line was drawn using the average Δ_L_ value measured experimentally. (F) Same as panel E but for C. crescentus.

Collectively, our data show that cells modulate their cell cycle time, and not their relative growth rate, to achieve the same length extension. As a result, the so-called ‘normalized cell cycle time’ αT is negatively dependent on Lb (Figure 4E, F). This negative dependence is often taken as supportive evidence for a sizer-based mechanism. The rationale for this is that if a cell needs to reach a certain size before committing to division, shorter cells at birth require longer cell cycle times. However, this negative dependence between αT and Lb is also expected from the constant extension model. In fact, if we used the average Δ_L_ values obtained from the E. coli and C. crescentus stalked cell experiments (Δ_L_ = 3.23 μm and Δ_L_ = 1.81 μm, respectively), we found that the analytical expression derived from the constant extension model (see SI, Eq. 5) describes the averaged data very well (Figure 4E,F).

The constant length extension between divisions changes with nutrient availability in E. coli

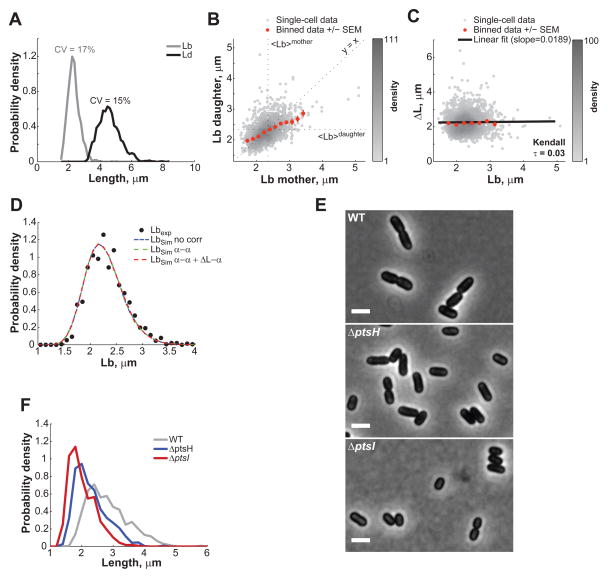
It is well known that E. coli changes its size in response to nutrient availability (Schaechter et al., 1958). If cell size homeostasis works through a constant elongation irrespective of the composition of the growth medium, we would expect the fixed cell length extension in nutrient-poor medium to be smaller than in the nutrient-rich LB medium, with the average Δ_L_ value matching the average Lb value for each growth medium. To test this hypothesis, we grew E. coli BW25113 in microfluidic chambers with M9 supplemented medium (M9 salts supplemented with 0.1% casaminoacids and 0.2% glucose) instead of LB medium. Under steady-growth conditions (Figure S4), the cell cycle time in M9 supplemented medium was longer than in LB medium with T = 42± 12 min, and the cell length at birth and at division were shifted to lower values (Figure 5A), with Lb = 2.32 ± 0.38 μm and Ld = 4.59 ± 0.71 μm. Cell size control in M9 medium remains precise, with CV values of 17% and 15% for Lb and Ld, respectively.

Figure 5. E. coli also controls its length through a constant elongation in M9 supplemented medium.

(A) Distribution of Lb and Ld of BW25113 cells (n = 1,528) grown in M9 supplemented medium at 32°C in a microfluidic chamber over 6 h. (B) Partial inheritance of Lb from one generation to the next. (C) Dependence of ΔL on Lb. The black line represents the linear fit to the single-cell data. (D) Experimental and simulated Lb distributions. ‘No corr’, ‘α-α’ and ‘α-α + ΔL_-α’ refer to the type of correlations included in the simulations (as described in SI). (E) Phase contrast images of BW25113 wild type, Δ_pstH and Δ_ptsI_ grown in M9 supplemented medium in liquid cultures and spotted on 1% agarose pads. The scale bars represents 2 μm. (F) Cell length distributions of wild-type, Δ_pstH_ and Δ_ptsI_ populations. See also Figure S4 and S5.

Importantly, as in rich medium, the correlation for the length at birth between mothers and daughters was ~0.5 (Figure 5B), as expected from the constant extension model. In addition, Δ_L_ and Lb remained uncorrelated (Kendall τ = 0.03, Figure 5C). Curiously, we observed correlations between some parameters (α of daughter vs. α of mother and Δ_L_ vs. α, Figure S5A-B) in the M9 data that were absent in the LB dataset (Figure S5C-D); however, these correlations had no impact on cell size regulation (Figure 5D, Figure S5E, see SI). Consistent with our hypothesis, cells elongated by a shorter increment before division occurs, with Δ_L_ = 2.26 ± 0.59 μm in M9 supplemented medium compared to 3.23 ± 0.6 μm in rich LB medium to set the corresponding length at birth. This suggests that cells modulate their average length by changing the average Δ_L_ in response to changes in nutrient availability.

If the latter is true, we reasoned that mutants impaired in the transport of the carbon source from the environment may behave as if they were growing in a carbon-poor medium: cells would implement a smaller average ΔL while fully maintaining size homeostasis (i.e., similar CV_ΔL_ as wild type). The phosphotransferase system (PTS) is involved in the efficient transport of sugars across the membrane. Deletion of genes encoding the core PTS components PtsH and PtsI in E. coli resulted in a reduced growth rate (> 2-fold) and a visibly shorter cell morphology in glucose-containing M9 supplemented medium (Figure 5E-F). The Δ_ptsH_ and Δ_ptsI_ mutants were also slightly thinner (data not shown). Consistent with our expectation, quantitative analysis (see SI) showed that disruption of glucose transport results in a marked reduction in average ΔL between divisions (<ΔL_> = 1.9 μm for wild type vs. 1.6 and 1.5 μm for Δ_ptsH and Δ_ptsI_, respectively), without changing the precision of the size homeostasis mechanism (CVΔL = 20% for wild type vs. 16 and 18% for Δ_ptsH_ and Δ_ptsI_, respectively). These data further support the notion that nutrient availability affects cell size by determining the targeted ΔL that cells will implement at each division cycle.

The constant extension mechanism has no memory

The constant extension mechanism is precise, but not perfect, as reflected by the CV of ΔL (Figure S3D, E). As such, ΔL values fluctuate around an average value (i.e., the targeted value) from cell-to-cell and from generation-to-generation. Importantly, the microfluidic data showed that the constant extension mechanism has no memory as the ΔL values of mother and daughter cells were not significantly correlated (Figure S5F-G, with τ = 0.10 and 0.03 for E. coli in M9 an LB media and with τ = 0.06 for C. crescentus, respectively). In other words, the accuracy of a cell in implementing the targeted ΔL has no bearing on the precision of its descendants.

Could the constant length extension be applied at a cell cycle event other than division?

So far, we have considered the case of a constant elongation being applied from one division to the next (Figure 6A). But what if the point of control for cell size homeostasis occurs at an earlier cell cycle event X, and completion of this event X triggers division after a constant amount of time, or timer δt, has elapsed? In this scenario, the constant elongation (referred to as Δ_L*_ to distinguish it from the elongation ΔL that we actually measured between consecutive divisions) would be applied at this event X, and not at division. For example, this early control event could be the initiation of DNA replication, as theoretically proposed before (Amir, 2014). This is an important consideration as DNA replication initiation is often assumed to control division. In a scenario where Δ_L*_ is applied at cell cycle event X, the division cycle would be shifted out of phase relative to the constant elongation cycle_,_ and division would follow the completion of a fixed elongation Δ_L*_ after a timer δt (Figure 6B-C). Could this scenario account for the experimental data we obtained?

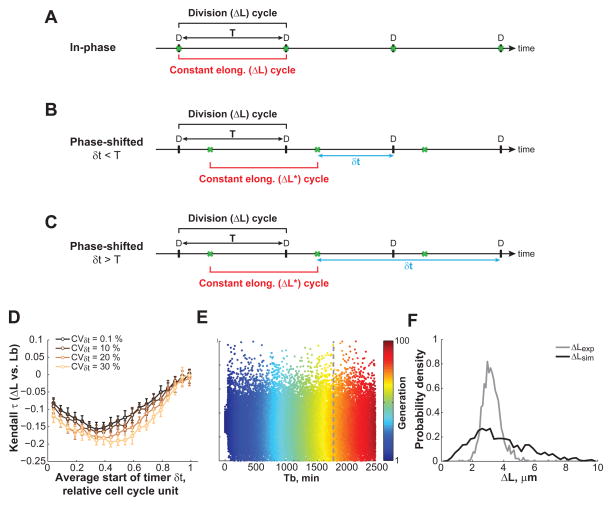
Figure 6. Testing the phase-shifted constant extension model.

(A) Schematic of the constant extension model in which the division cycle (black bracket) is in phase with the constant elongation cycle (red bracket). The event under cell cycle control (green crosses) is division D. (B) Schematic of the ‘phase-shifted’ model with a timer δt < _T._ In this model, the elongation increment (_ΔL*_) is applied to a cell cycle event X (green crosses) that is coupled to division by a timer _δt_ shorter than the interdivision time _T_. (C) Schematic representation of the ‘phase-shifted’ constant extension model with _δt_ > T and with the constraint of a single event X per division cycle (see SI and Table S1). (D) Simulations of the ‘phase-shifted’ model with a timer δt < _T_ (see SI and Table S1). The Kendall correlation coefficient between _Lb_ and _ΔL_ depends on how early in the cell cycle the timer _δt_ starts. Shown is the mean ± standard deviation of 10 simulations performed with 1,500 cells for _DR_ = 0.56. (E) Simulations of the ‘phase-shifted’ model with a timer _δt_ > T. Shown is a scatter plot of ΔL (from birth to division) for 500 simulated cells at each generation. (F) Same as (E), but plot showing the distribution of ΔL at the time indicated by the dashed line in panel E. See also Figure S6.

First, we considered the case where the timer δt is shorter than the interdivision time T (Figure 6B). This would illustrate the C. crescentus situation (T = 100 min) in which DNA replication initiates early in the cell cycle and completes before division (McAdams and Shapiro, 2009). Simulations of the phase-shifted model showed significant discrepancies with the experimental C. crescentus data for any timer that starts, on average, earlier than at 80% of the division cycle (i.e., for any timer δt > 20 min for T = 100 min). For example, in the phase-shifted model, ΔL (cell length extension between consecutive divisions) and Lb show a significant negative correlation (Figure 6D), in contrast to what was observed experimentally (Figure 1G). Other relationships between variables were also inconsistent with the experimental data (Figure S6A-C). Therefore, a constant elongation is unlikely to be applied at DNA replication initiation — or any other early cell cycle event — to control cell size homeostasis in C. crescentus. Whether division was asymmetric (Figure 6D and S6A-C) or symmetric (Figure S6D-F) did not alter the conclusion.

We also considered the relevant case in which the timer δt would be longer than the interdivision time T (Figure 6C). Previous work has proposed that in E. coli, DNA replication initiation and cell division are separated by a constant timer of about 60 min (Cooper and Helmstetter, 1968), which would exceed the doubling times of 27 and 42 min we observed for E. coli growing in LB and M9 growth media, respectively. To consider these fast-growth cases, we ran simulations of the phase-shifted model with timers longer than the interdivision times. They resulted in the generation of widely abnormal cell size distributions (Figure S6G-H), which arose from the fluctuation in number of event X (e.g., DNA replication initiation) occurring between two divisions. Even when event X was forced to happen exactly once per division cycle (by adding constraining rules to the model, see SI) to reduce the Lb variability, the ΔL values remained aberrantly variable (Figure 6E-F). Furthermore, the cell length extension between divisions (ΔL) was correlated between mothers and daughters in the simulated data (Figure S6I), that is, this phase-shifted model with δt > T displays memory because the constant elongation ΔL* overlaps with two consecutive division cycles (Figure 6C). This correlation in ΔL between mothers and daughters is in contradiction with the experimental data (compare Figure S5F-G with Figure S6I).

Collectively, these experimental results are inconsistent with the hypothesis that the constant elongation is applied at the initiation of DNA replication or any cell cycle event that occurs within the first 80% of the interdivision time. This also excludes the formation of the FtsZ cytokinetic ring, implying that this event is unlikely to dictate the timing of cell division. This is in agreement with single-cell observations that FtsZ ring formation and cell constriction are uncorrelated in time (Tsukanov et al., 2011). Our analysis suggests that the cycles of constant elongation and division are in phase or close to it (Figure 6A), indicating that a late cell cycle stage is the control point. For instance, a late cell cycle event (e.g., a late step of chromosome segregation potentially sensed by FtsK) may communicate with the cell division machinery to trigger FtsZ ring constriction. Division would then restart a cycle of constant length extension.

The constant extension mechanism is robust with respect to cell length and division positioning

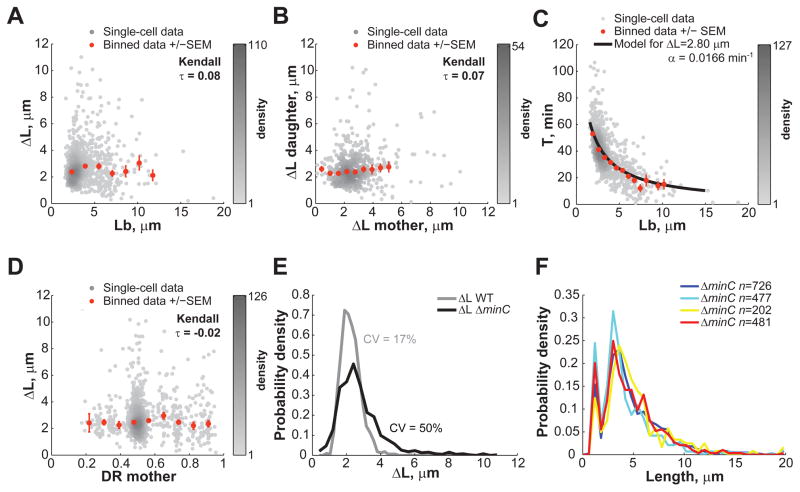
In the constant extension model, cell size homeostasis is based on a simple governing principle: cells trigger division once they have elongated the targeted ΔL (± noise). Does the simple rule of adding a constant length still apply when cells are aberrantly long or when division is misplaced? To address this question, we carried out microfluidic experiments with the E. coli Δ_minC_ mutant (Movie S3). Without MinC, the min system that regulates the precision of FtsZ ring placement is defective; as a result, cells divide not only at midcell, but also at polar, DNA-free regions, resulting in the appearance of minicells (Adler et al., 1967). As expected, the large imprecision in division placement in the Δ_minC_ mutant lead to very wide distribution of cell lengths at birth (CV of Lb = 52%). But despite these aberrations, Δ_minC_ cells elongated a constant amount between divisions, regardless of their length at birth (Figure 7A, Kendall τ=0.08; anucleate minicells were excluded from the analysis as they do not grow). Even very long cells grew, on average, the same amount as short cells before dividing (Figure 7A). Thus, the constant extension mechanism is insensitive to cell length, as predicted by the model.

Figure 7. The constant extension mechanism is robust with respect to the cell length and division site placement.

E. coli BW25113 Δ_minC_ cells were grown in microfluidic chambers at 30°C in M9 supplemented medium over 5.5 h. (A) Dependence of ΔL on Lb (n = 959 cells). Grey dots represent single-cell data while orange dots represent the average of binned data ± SEM. (B) Degree of inheritance of ΔL over one generation (n = 510 cells). (C) Dependence of the cell cycle time T on Lb (n = 959 cells). The black line represents the expected average αT from the constant elongation model as described by the equation T = ln(1+Δ_L_/Lb)/α. The black line was drawn using the average Δ_L_ and α values measured experimentally. (D) Dependence of ΔL on DR. (E) Distributions of length extensions for wild-type and Δ_minC_ cells. (F) Cell length distributions of BW25113 Δ_minC_ cells grown in separate 2-mL liquid cultures in M9 supplemented medium. See also Movie S3.

Similarly to what was observed for wild-type cells, there was no memory with respect to elongation for Δ_minC_ cells, as ΔL between mothers and daughters remained uncorrelated (Figure 7B). Also, as shown in Figure 7C, constant elongation in Δ_minC_ cells was achieved by modulating the interdivision time T (and not the growth rate, data not shown). The Δ_minC_ data showcased the striking agreement between the average cell behavior and the analytical expression of the constant extension model over a wide range of cell lengths (binned data vs. black line, Figure 7C).

The Δ_minC_ data also demonstrated that cell elongation is independent of where division occurs (Figure 7D). Even when a division occurred at a pole (producing a minicell), the viable offspring, which inherited all of the genetic material and most of the cytoplasmic and membrane content of the mother, implemented a constant elongation just like cells generated by a normal division. Thus, it is the process of division itself, and not the partitioning of cellular content, that resets the constant extension mechanism.

Another interesting aspect of the Δ_minC_ mutant is that it has a moderate chromosome segregation defect (Jaffe et al., 1988) and a skewed distribution of ΔL toward higher values (Figure 7E). We envision two possibilities by which a partial DNA segregation defect can result in tailed ΔL distribution:

DNA segregation may be part of a fail-safe or checkpoint mechanism that is superimposed over the constant extension mechanism. In this scenario, chromosome segregation would normally occur within the time needed to grow the appropriate ΔL and divide, having no impact on the constant extension mechanism. However, if DNA segregation become abnormal and does not complete within this time period, a fail-safe mechanism would override the constant extension mechanism by delaying division. Such override may occur through so-called ‘nucleoid occlusion’ (Wu and Errington, 2012), which is known to interfere with FtsZ ring assembly in E. coli. A delay in division would result in higher ΔL values than expected. Note that any fail-safe mechanism that blocks a step required for division as a response to a defect would override the constant extension mechanism until the defect is resolved. A good example is the SOS response to DNA damage that blocks division until DNA repair is completed (Huisman and D’Ari, 1981).

Alternatively, DNA segregation may be an inherent part of the constant extension mechanism, with the nucleoid acting as a molecular ruler. For example, cell extension may be involved in nucleoid separation, which in turn may trigger cell constriction, perhaps by relieving some form of DNA occlusion. A defect in DNA segregation would then delay division, leading to higher ΔL values. Future studies will be required to distinguish between these two possibilities.

Defining features of the constant extension mechanism

A constant extension mechanism strongly departs conceptually from the deeply rooted critical size paradigm. In all sizer-based models, cells ‘sense’ how big they are, whereas in the constant extension model, cells are blind to their size, and instead ‘sense’ how much they have grown. It is important to note that although we are measuring cell length, cells may be ‘measuring’ a difference in any cell size parameter; it could be a difference in cell length but it could also be a difference in cell mass, surface area or volume since cell width does not change during the cell cycle.

Our findings suggest that cells follow the simple rule of triggering division when they have elongated the targeted ΔL. This is sufficient to provide a cell size homeostasis mechanism. We have identified several defining features of this cell size homeostasis mechanism. i) Cell size deviations are abated exponentially over generations (Figure 3J). ii) The constant extension mechanism does not need to be precise (Figure 3), with experimental CVΔL of 19–26%. A greater variability in ΔL among cells would increase the variability in cell length at birth but would not affect the average cell length of the population or the homeostatic capability of the mechanism. iii) The constant extension mechanism provides cell size homeostasis that is robust with respect to cell length and division placement. Our Δ_minC_ data explicitly demonstrate the robustness of the mechanism: despite aberrant cell lengths at birth, wide imprecision of division placement and large variation in cell elongation, Δ_minC_ cells maintain a stable cell size distribution over time (data not shown) and from culture to culture (Figure 7F). iv) Any division, including non-productive ones that create minicells, resets the constant extension mechanism. v) Any imprecision in size extension at one generation has no impact on the precision at the next generation (Figure S5F, G). These defining features provide a strong foundation for future molecular studies, and will have to be accounted for by any molecular models of the constant extension mechanism.

Several lines of evidence suggest that a constant cell extension might be an ancient and broadly applicable means of achieving cell size homeostasis. E. coli and C. crescentus are evolutionary distant, having diverged over a billion year ago. Their divisions (symmetric versus asymmetric) are distinct. E. coli changes its length according to nutrient availability whereas C. crescentus does not. E. coli can undergo overlapping rounds of DNA replication, while this has never been observed for C. crescentus. Despite these profound differences in growth, division and replication cycle, a similar cell size control operates, suggesting that this size homeostatic model is applicable to a wide variety of bacterial species under different growth conditions.

Experimental procedures

Strains and media

C. crescentus CB15N (Evinger and Agabian, 1977) and Escherichia coli K12 strain BW25113 (Datsenko and Wanner, 2000) were used for the experiments unless indicated. E. coli BW25113 and Δ_minC_, Δ_ptsH_ and Δ_ptsI_ derivatives were obtained from the Yale E. coli Genetic stock center. C. crescentus CB15N was grown either in PYE medium (2 g/L bacto-peptone, 1 g/L yeast extract, 1 mM MgSO4, 0.5 mM CaCl2) or M2G medium (0.87 g/L Na2HPO4, 0.54 g/L KH2PO4, 0.50 g/L NH4Cl, 0.2 % (w/v) glucose, 0.5 mM MgSO4, 0.5 mM CaCl2, 0.01 mM FeSO4). E. coli BW25113 was grown in LB medium (10 g/L NaCL, 5 g/L yeast extract, 10 g/L tryptone) or M9 supplemented medium (6 g/l Na2HPO4·7H2O, 3 g/L KH2PO4, 0.5 g/L NaCl, 1 g NH4Cl, 2 mM MgSO4, 1 μg/L thiamine supplemented with 0.1% casamino acids and 0.2% glucose).

Microscopy

C. crescentus cells were grown up to exponential phase (OD660nm < 0.3) and spotted on 0.3% agarose pads containing M2G medium, unless specified otherwise. Microscopy was performed on an Eclipse 80i microscope (Nikon, Tokyo, Japan) equipped with a phase-contrast objective Plan Apochromat 100×/1.40 NA (Nikon, Tokyo, Japan), an Orca-II-ER (Hamamatsu Photonics, Hamamatsu City, Japan) and an Andor iXon DU-897E camera (Andor Technology Ltd., Belfast, UK) with 2× optivar. Images were acquired every 2.5 min using MetaMorph software (Molecular Devices, Sunnyvale, CA, USA). For still images of E. coli strains, cells were grown at 30°C up to exponential phase (OD600nm<0.3) and spotted on 1% agarose pads. For microfluidic experiments, E. coli cells were loaded and grown for at least 5 generations in the microfluidic device prior to imaging. Microscopy was performed on an Eclipse Ti-E microscope (Nikon, Tokyo, Japan) equipped with Perfect Focus System (Nikon, Tokyo, Japan) and an Orca-R2 camera (Hamamatsu Photonics, Hamamatsu City, Japan) and a phase-contrast objective Plan Apochromat 100×/1.45 NA (Nikon, Tokyo, Japan). Time-lapse images were acquired every 5 sec using NIS-Element Ar software (Nikon Instruments INC., Melville, NY USA).

Supplementary Material

1. Figure S1: E. coli cells experience the same environment over the entire microfluidic chamber. Related to Figure 2.

(A) Image (left) and schematic (right) of one chamber filled with E. coli BW25113 cells growing in LB medium. The dimensions of the chamber and the flow of the medium are indicated by the broken lines and bold arrows, respectively. (B) Two-dimensional histograms (shown as a heat map) for the elongation ΔL, the length at birth Lb, the cell cycle time T, and the elongation rate α as a function of the position of each cell in the chamber at the time of division. The color scales are centered on the mean ± 2 standard deviations for each variable. This interval encompasses ~95% of the cells (n = 1,305). The grey color on the heat maps indicates an area of the chamber at which no cell has divided during the course of the experiment.

2. Figure S2: ΔL and Lb are independent for other E. coli strains grown at 37°C. Related to Figure 2.

(A) Relationship between ΔL and Lb for E. coli MG1655 cells (n = 4,612) grown in LB medium at 37°C. The raw data were obtained from Wang et al. (2010) via http://jun.ucsd.edu/mother_machine.php. The black line represents the linear fit to single-cell data. (B) Same as (A) but for E. coli B/r cells (n = 7,620).

3. Figure S3: Analysis of experimental distributions. Related to Figure 3.

(A) Plot showing the Lb distributions for C. crescentus stalked and swarmer cells from experiments and simulations. (B) Comparison between the simulated and experimental Lb and ΔL distributions for E. coli BW25113 cells (LB dataset). (C) Comparison between the simulated and experimental Lb and ΔL of C. crescentus CB15N cells. (D) Dependence of the CV of the length at birth (CV_Lb_) with the CV of the elongation (CVΔ_L_) for different values of the CV of the division ratio (CV_DR_). The lines represent the theoretical dependence from the constant extension model (see SI, Eq. 15 for the analytical expression) while the circles represent the result of the simulations. The experimental results are displayed as black crosses. (E) Magnified view of the area boxed in dashed lines in (D).

4. Figure S4: Homogeneous and steady state growth of E. coli cells in microfluidic chambers with M9 supplemented medium. Related to Figure 5.

(A) Maintenance of a stable growth rate α over the course of the 6h-long experiment (n = 1,528 cells). (B) Same as (A) but for Lb (n = 1,528 cells). (C) Representative growth curve of a single cell (black circles). Length was measured every 5 sec. The data were fitted by an exponential function represented by the red line. (D) Two-dimensional histograms (shown as a heat map) of ΔL, Lb, the cell cycle time T and α as a function of each cell position at division. The color scales are centered on the mean ± 2 standard deviations for each variable. This interval encompasses ~95% of the cells.

5. Figure S5: Correlations between various parameters for the E. coli and C. crescentus datasets. Related to Figures 1, 2, 3 and 5.

For E. coli BW25113 cells grown in microfluidic chambers: (A) Degree of inheritance of α over one generation in M9 supplemented medium (n = 1,203 cells). (B) Dependence of ΔL on α in M9 supplemented medium(n = 1,528 cells). (C) Degree of inheritance of α over one generation in LB medium (n = 1,025 cells). (D) Dependence of ΔL on α in LB medium (n = 1,305 cells). (E) Plot showing the simulated dependence of Lb and L when the levels of correlation shown in (A) and (B) are taken into account (n > 60,000 virtual cells). (F) Degree of inheritance of ΔL over one generation (n = 1,203 cells) in M9 supplemented medium. (G) Degree of inheritance of ΔL over one generation in LB medium (n = 1,025 cells). (H) Dependence of DR on ΔL in M9 suppelemented medium (n = 1,528 cells). (I) Dependence of DR on ΔL in LB medium(n = 1,305 cells).

For C. crescentus grown on M2G soft-agar pads: (J) Dependence of ΔL on α (n = 565 cells). (K) Degree of inheritance of α over one generation (n = 457 cells). (L) Dependence of DR on ΔL (n = 565 cells).

6. Figure S6: Phase-shifted constant extension model coupled to a timer longer than the interdivision time. Related to Figure 6.

We simulated the phase-shifted model applied to a cell cycle event X coupled to division through a timer δt > T (see SI and Table S1). (A) Kendall correlation coefficients for ΔL between mother and daughter cells as a function of the timer starting time. DR was 0.56 to reflect the experimental division ratio for C. crescentus. The error bars shows the standard deviation obtained from 10 simulations performed with 1,500 cells. (B) Kendall correlation coefficients between α and T as a function of the timer starting time. DR = 0.56. (C) Scatter plot illustrating the experimental dependence of T on α for C. crescentus stalked cells (n = 457 cells). (D) Same plot as Figure 6D for DR = 0.5. (E) and (F) are the same plots as panels A and B, respectively, for DR = 0.5. (G) Plot showing Lb versus time at birth (Tb) for simulations of the phase-shifted model with δt > T. (H) Plot showing the Lb distribution at the time indicated by the dashed line in (G) compared to the experimental distribution. (I) Plot showing the correlation between ΔL (from birth to division) of mother and daughter cells in data obtained from simulations of a phase-shifted model with δt > T and with the extra requirement that the cell cycle event X occurs only once per division cycle (see SI and Table S1).

7. Figure S7: Analysis of experimental distributions and relationships. Related to Figures 1 and 2.

From (A) to (D), results from E. coli BW25113 cells (n = 1,305) grown in microfluidic chambers at 30°C in LB medium. (A) The experimental distribution of ΔL is consistent with a log-normal distribution. (B) The experimental distribution of DR appears Gaussian. (C) The relative growth rate α distribution was also well fitted by a Gaussian. (D) Relationship between DR and Lb. (E) Same as (D) but for C. crescentus stalked cells (n = 565) grown at 30°C in M2G medium on 0.3% agarose pads.

8. Movie S1: C. crescentus grows and divides on a soft-agar pad. Related to Figure 1.

Movie showing a time lapse of one C. crescentus stalked cell growing and dividing on a soft (0.3%) agar M2G pad. The swarmer progeny swims away following division. Occasionally, an escaped swarmer cell immobilizes on the pad. Such an event is highlighted by a white arrow near the end of the movie.

9. Movie S2: E. coli BW25113 growing in a microfluidic chamber. Related to Figure 2.

Movie showing a time-lapse sequence of E. coli cells growing in a microfluidic chamber in LB medium at 30°C. The medium flows from left to right at the top and bottom of the chamber. Cells pushed outside the microfluidic chamber (by the growth of other cells) are washed away with the flow. The scale bar on the top left represents 2μm.

10. Movie S3: E. coli BW25113 ΔminC growing in a microfluidic chamber. Related to Figure 7.

Movie showing a time-lapse sequence of E. coli ΔminC cells growing in a microfluidic chamber in M9 supplemented medium at 30°C. The medium flows from left to right at the top and bottom of the chamber. Cells pushed outside the microfluidic chamber (by the growth of other cells) are washed away with the flow. The scale bar on the top left represents 2μm.

Table S1: Default input parameter values used in simulations of the constant extension models

Model 1: Constant elongation increment in phase with the division cycle.

Model 2: Constant extension model shifted in phase with respect to the division cycle. The constant elongation increment is applied to a cell cycle event X that is coupled to division through a timer.

Model 3: Same as model 2 with a number of occurrences of event X per division cycle fixed to 1 as specified in the SI.

Highlights.

Bacterial cell elongation over a cell cycle is independent of cell length at birth.
To control their size, cells sense how much they have grown, not how big they are.
The constant size extension occurs between divisions.
This mechanism is extremely robust and broadly applicable.

Acknowledgments

We would like to thank Dr. Johan Elf for sharing the design of his microfluidic device, Matts Walden and Jason Hocking for help setting up the microfluidic system in our laboratory, and the Yale E. coli Genetic stock center for the E. coli BW25113 derived strains. This work was in part supported by the National Institute of Health (R01 GM065835 to C.J.-W.). S.K. and S.E.E. were in part supported by the Astellas Foundation for Research on Metabolic Disorders and a predoctoral training grant of the National Institute of Health (5 T32 GM 7223-39), respectively. We are also grateful to the staffs of the Yale University Faculty of Arts and Sciences High Performance Computing Center for support, and to the members of the Jacobs-Wagner laboratory for fruitful discussions and for critical reading of this manuscript. C.J.-W. is an investigator of the Howard Hughes Medical Institute.

Footnotes

Supplemental information

The SI includes: microfluidic device manufacturing, image and data processing, data analysis, the description of the mathematical models introduced in the Results section, the procedures used for the stochastic simulations of these models as well as supplementary figures, movies and their legends.

Author Contributions

M.C., I.V.S. and S.K. contributed equally to this work. S.K., M.C. and C.J.-W. conceived the project, designed the experiments and analyzed the data. M.C., S.K. and S.E. performed the experiments. I.V.S. and B.B. developed mathematical models and I.V.S., B.B. and M.C. performed simulations. A.P. assisted in data analysis. M.C., I.V.S. and C.J.-W. wrote the paper. All authors commented on and approved the paper.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

Adler HI, Fisher WD, Cohen A, Hardigree AA. Miniature escherichia coli cells deficient in DNA. Proc Natl Acad Sci USA. 1967;57:321–326. doi: 10.1073/pnas.57.2.321. [DOI] [PMC free article] [PubMed] [Google Scholar]
Akerlund T, Nordstrom K, Bernander R. Analysis of cell size and DNA content in exponentially growing and stationary-phase batch cultures of Escherichia coli. J Bacteriol. 1995;177:6791–6797. doi: 10.1128/jb.177.23.6791-6797.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
Amir A. Cell Size Regulation in Bacteria. Phys Rev Lett. 2014:112. [Google Scholar]
Bates D, Kleckner N. Chromosome and replisome dynamics in E. coli: loss of sister cohesion triggers global chromosome movement and mediates chromosome segregation. Cell. 2005;121:899–911. doi: 10.1016/j.cell.2005.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
Boye E, Nordstrom K. Coupling the cell cycle to cell growth. EMBO Rep. 2003;4:757–760. doi: 10.1038/sj.embor.embor895. [DOI] [PMC free article] [PubMed] [Google Scholar]
Cooper S. Biochemistry and regulation of prokaryotic and eukaryotic division cycles. 11. Academic Press; 1991. Bacterial growth and division. [Google Scholar]
Cooper S, Helmstetter CE. Chromosome replication and the division cycle of Escherichia coli B/r. J Mol Biol. 1968;31:519–540. doi: 10.1016/0022-2836(68)90425-7. [DOI] [PubMed] [Google Scholar]
Datsenko KA, Wanner BL. One-step inactivation of chromosomal genes in Escherichia coli K-12 using PCR products. Proc Natl Acad Sci USA. 2000;97:6640–6645. doi: 10.1073/pnas.120163297. [DOI] [PMC free article] [PubMed] [Google Scholar]
Di Talia S, Skotheim JM, Bean JM, Siggia ED, Cross FR. The effects of molecular noise and size control on variability in the budding yeast cell cycle. Nature. 2007;448:947–951. doi: 10.1038/nature06072. [DOI] [PubMed] [Google Scholar]
Donachie WD. Relationship between cell size and time of initiation of DNA replication. Nature. 1968;219:1077–1079. doi: 10.1038/2191077a0. [DOI] [PubMed] [Google Scholar]
Evinger M, Agabian N. Envelope-Associated Nucleoid from Caulobacter-Crescentus Stalked and Swarmer Cells. J Bacteriol. 1977;132:294–301. doi: 10.1128/jb.132.1.294-301.1977. [DOI] [PMC free article] [PubMed] [Google Scholar]
Evinger M, Agabian N. Caulobacter crescentus nucleoid: analysis of sedimentation behavior and protein composition during the cell cycle. Proc Natl Acad Sci USA. 1979;76:175–178. doi: 10.1073/pnas.76.1.175. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fantes PA. Control of cell size and cycle time in Schizosaccharomyces pombe. J Cell Sci. 1977;24:51–67. doi: 10.1242/jcs.24.1.51. [DOI] [PubMed] [Google Scholar]
Fantes PA, Nurse P. Division timing: controls, models and mechanisms. In: John PCL, editor. The cell cycle. Cambridge University Press; 1981. pp. 11–34. [Google Scholar]
Harris LK, Dye NA, Theriot JA. A Caulobacter MreB mutant with irregular cell shape exhibits compensatory widening to maintain a preferred surface area to volume ratio. Mol Microbiol. 2014 doi: 10.1111/mmi.12811. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hosoda K, Matsuura T, Suzuki H, Yomo T. Origin of lognormal-like distributions with a common width in a growth and division process. P Phys Rev E Stat Nonlin Soft Matter Phys. 2011;83:031118. doi: 10.1103/PhysRevE.83.031118. [DOI] [PubMed] [Google Scholar]
Huisman O, D’Ari R. An inducible DNA replication-cell division coupling mechanism in E. coli. Nature. 1981;290:797–799. doi: 10.1038/290797a0. [DOI] [PubMed] [Google Scholar]
Jaffe A, D’Ari R, Hiraga S. Minicell-forming mutants of Escherichia coli: production of minicells and anucleate rods. J Bacteriol. 1988;170:3094–3101. doi: 10.1128/jb.170.7.3094-3101.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
Johnston GC, Pringle JR, Hartwell LH. Coordination of growth with cell division in the yeast Saccharomyces cerevisiae. Exp Cell Res. 1977;105:79–98. doi: 10.1016/0014-4827(77)90154-9. [DOI] [PubMed] [Google Scholar]
Koch AL, Schaechter M. A model for statistics of the cell division process. J Gen Microbiol. 1962;29:435–454. doi: 10.1099/00221287-29-3-435. [DOI] [PubMed] [Google Scholar]
Koppes LJ, Meyer M, Oonk HB, de Jong MA, Nanninga N. Correlation between size and age at different events in the cell division cycle of Escherichia coli. J Bacteriol. 1980;143:1241–1252. doi: 10.1128/jb.143.3.1241-1252.1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lord PG, Wheals AE. Variability in individual cell cycles of Saccharomyces cerevisiae. J Cell Sci. 1981;50:361–376. doi: 10.1242/jcs.50.1.361. [DOI] [PubMed] [Google Scholar]
McAdams HH, Shapiro L. System-level design of bacterial cell cycle control. FEBS lett. 2009;583:3984–3991. doi: 10.1016/j.febslet.2009.09.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
Osella M, Nugent E, Cosentino Lagomarsino M. Concerted control of Escherichia coli cell division. Proc Natl Acad Sci USA. 2014;111:3431–3435. doi: 10.1073/pnas.1313715111. [DOI] [PMC free article] [PubMed] [Google Scholar]
Robert L, Hoffmann M, Krell N, Aymerich S, Robert J, Doumic M. Division in Escherichia coli is triggered by a size-sensing rather than a timing mechanism. BMC biol. 2014;12:17. doi: 10.1186/1741-7007-12-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
Santi I, Dhar N, Bousbaine D, Wakamoto Y, McKinney JD. Single-cell dynamics of the chromosome replication and cell division cycles in mycobacteria. Nat Commun. 2013;4:2470. doi: 10.1038/ncomms3470. [DOI] [PubMed] [Google Scholar]
Schaechter M, Maaloe O, Kjeldgaard NO. Dependency on medium and temperature of cell size and chemical composition during balanced grown of Salmonella typhimurium. J Gen Microbiol. 1958;19:592–606. doi: 10.1099/00221287-19-3-592. [DOI] [PubMed] [Google Scholar]
Schaechter M, Williamson JP, Hood JR, Jr, Koch AL. Growth, cell and nuclear divisions in some bacteria. J Gen Microbiol. 1962;29:421–434. doi: 10.1099/00221287-29-3-421. [DOI] [PubMed] [Google Scholar]
Siegal-Gaskins D, Crosson S. Tightly regulated and heritable division control in single bacterial cells. Biophys J. 2008;95:2063–2072. doi: 10.1529/biophysj.108.128785. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sliusarenko O, Heinritz J, Emonet T, Jacobs-Wagner C. High-throughput, subpixel precision analysis of bacterial morphogenesis and intracellular spatio-temporal dynamics. Mol Microbiol. 2011;80:612–627. doi: 10.1111/j.1365-2958.2011.07579.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sveiczer A, Novak B, Mitchison JM. The size control of fission yeast revisited. J Cell Sci. 1996;109(Pt 12):2947–2957. doi: 10.1242/jcs.109.12.2947. [DOI] [PubMed] [Google Scholar]
Terrana B, Newton A. Pattern of unequal cell division and development in Caulobacter crescentus. Dev Biol. 1975;44:380–385. doi: 10.1016/0012-1606(75)90409-1. [DOI] [PubMed] [Google Scholar]
Tsukanov R, Reshes G, Carmon G, Fischer-Friedrich E, Gov NS, Fishov I, Feingold M. Timing of Z-ring localization in Escherichia coli. Phys Biol. 2011;8:066003. doi: 10.1088/1478-3975/8/6/066003. [DOI] [PubMed] [Google Scholar]
Turner JJ, Ewald JC, Skotheim JM. Cell size control in yeast. Curr Biol : CB. 2012;22:R350–359. doi: 10.1016/j.cub.2012.02.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ullman G, Wallden M, Marklund EG, Mahmutovic A, Razinkov I, Elf J. High-throughput gene expression analysis at the level of single proteins using a microfluidic turbidostat and automated cell tracking. Philos Trans R Soc Lond B Biol Sci. 2013;368:20120025. doi: 10.1098/rstb.2012.0025. [DOI] [PMC free article] [PubMed] [Google Scholar]
Voorn WJ, Koppes LJ. Skew or third moment of bacterial generation times. Arch Microbiol. 1998;169:43–51. doi: 10.1007/s002030050539. [DOI] [PubMed] [Google Scholar]
Wakamoto Y, Ramsden J, Yasuda K. Single-cell growth and division dynamics showing epigenetic correlations. Analyst. 2005;130:311–317. doi: 10.1039/b409860a. [DOI] [PubMed] [Google Scholar]
Wang P, Robert L, Pelletier J, Dang WL, Taddei F, Wright A, Jun S. Robust growth of Escherichia coli. Curr Biol : CB. 2010;20:1099–1103. doi: 10.1016/j.cub.2010.04.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wold S, Skarstad K, Steen HB, Stokke T, Boye E. The initiation mass for DNA replication in Escherichia coli K-12 is dependent on growth rate. EMBO J. 1994;13:2097–2102. doi: 10.1002/j.1460-2075.1994.tb06485.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wu LJ, Errington J. Nucleoid occlusion and bacterial cell division. Nat Rev Microbiol. 2012;10:8–12. doi: 10.1038/nrmicro2671. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials