A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research (original) (raw)
Abstract
Objective
Intraclass correlation coefficient (ICC) is a widely used reliability index in test-retest, intrarater, and interrater reliability analyses. This article introduces the basic concept of ICC in the content of reliability analysis.
Discussion for Researchers
There are 10 forms of ICCs. Because each form involves distinct assumptions in their calculation and will lead to different interpretations, researchers should explicitly specify the ICC form they used in their calculation. A thorough review of the research design is needed in selecting the appropriate form of ICC to evaluate reliability. The best practice of reporting ICC should include software information, “model,” “type,” and “definition” selections.
Discussion for Readers
When coming across an article that includes ICC, readers should first check whether information about the ICC form has been reported and if an appropriate ICC form was used. Based on the 95% confident interval of the ICC estimate, values less than 0.5, between 0.5 and 0.75, between 0.75 and 0.9, and greater than 0.90 are indicative of poor, moderate, good, and excellent reliability, respectively.
Conclusion
This article provides a practical guideline for clinical researchers to choose the correct form of ICC and suggests the best practice of reporting ICC parameters in scientific publications. This article also gives readers an appreciation for what to look for when coming across ICC while reading an article.
Key indexing terms: Reliability and validity, Research, Statistics
Introduction
Before any measurement instruments or assessment tools can be used for research or clinical applications, their reliability must be established. Reliability is defined as the extent to which measurements can be replicated.1 In other words, it reflects not only degree of correlation but also agreement between measurements.2, 3 Mathematically, reliability represents a ratio of true variance over true variance plus error variance.4, 5 This concept is illustrated in Table 1. As indicated in the calculation, reliability value ranges between 0 and 1, with values closer to 1 representing stronger reliability. Historically, Pearson correlation coefficient, paired t test, and Bland-Altman plot have been used to evaluate reliability.3, 6, 7, 8 However, paired t test and Bland-Altman plot are methods for analyzing agreement, and Pearson correlation coefficient is only a measure of correlation, and hence, they are nonideal measures of reliability. A more desirable measure of reliability should reflect both degree of correlation and agreement between measurements. Intraclass correlation coefficient (ICC) is such as an index.
Table 1.
Hypothetical Flexion-Extension Range of Motion (ROM) of L4-L5 Measured by Radiograph
| Subject | Measured ROM | True ROM | Error |
|---|---|---|---|
| 1 | 28° | 28° | 0° |
| 2 | 20° | 20° | 0° |
| 3 | 24° | 20° | 4° |
| 4 | 18° | 22° | − 4° |
| 5 | 26° | 22° | 4° |
| 6 | 16° | 20° | − 4° |
| Variance | 22.4° | 9.6° | 12.8° |
Intraclass correlation coefficient was first introduced by Fisher9 in 1954 as a modification of Pearson correlation coefficient. However, modern ICC is calculated by mean squares (ie, estimates of the population variances based on the variability among a given set of measures) obtained through analysis of variance. Nowadays, ICC has been widely used in conservative care medicine to evaluate interrater, test-retest, and intrarater reliability (see Table 2 for their definitions).10, 11, 12, 13, 14, 15, 16, 17 These evaluations are fundamental to clinical assessment because, without them, we have no confidence in our measurements, nor can we draw any rational conclusions from our measurements.
Table 2.
Definitions of Different Types of Reliability
| Types | Definitions |
|---|---|
| Interrater reliability | It reflects the variation between 2 or more raters who measure the same group of subjects. |
| Test-retest reliability | It reflects the variation in measurements taken by an instrument on the same subject under the same conditions. It is generally indicative of reliability in situations when raters are not involved or rater effect is neglectable, such as self-report survey instrument. |
| Intrarater reliability | It reflects the variation of data measured by 1 rater across 2 or more trials. |
There are different forms of ICC that can give different results when applied to the same set of data, and the ways for reporting ICC may vary between researchers. Given that different forms of ICC involve distinct assumptions in their calculations and will lead to different interpretations, it is important that researchers are aware of the correct application of each form of ICC, use the appropriate form in their analyses, and accurately report the form they used. The purpose of this article is to provide a practical guideline for clinical researchers to choose the correct form of ICC for their reliability analyses and suggest the best practice of reporting ICC parameters in scientific publications. This article also aims to guide readers to understand the basic concept of ICC so that they can apply it to better interpret the reliability data while reading an article with related topics.
Discussion for Researchers
How to Select the Correct ICC Form for Interrater Reliability Studies
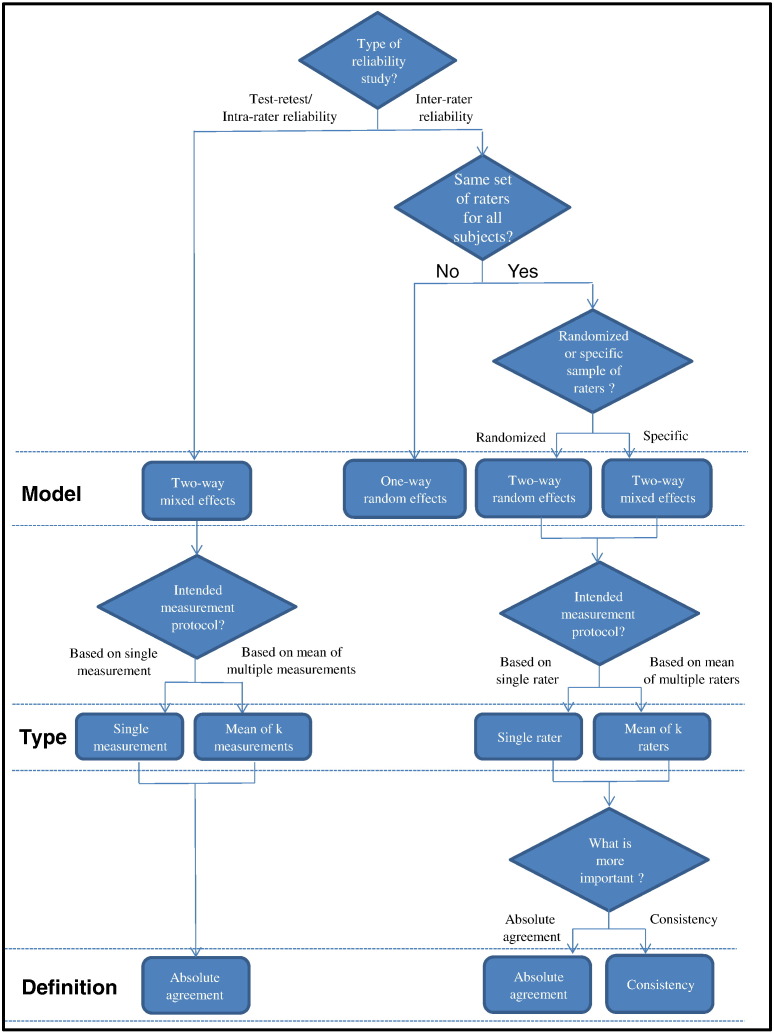
McGraw and Wong18 defined 10 forms of ICC based on the “Model” (1-way random effects, 2-way random effects, or 2-way fixed effects), the “Type” (single rater/measurement or the mean of k raters/measurements), and the “Definition” of relationship considered to be important (consistency or absolute agreement). These ICC forms and their formulation are summarized in Table 3.
Table 3.
Equivalent ICC Forms Between Shrout and Fleiss (1979) and McGraw and Wong (1996)
| McGraw and Wong (1996) Conventiona | Shrout and Fleiss (1979) Conventionb | Formulas for Calculating ICCc |
|---|---|---|
| One-way random effects, absolute agreement, single rater/measurement | ICC (1,1) | MSR−MSWMSR+k+1MSW |
| Two-way random effects, consistency, single rater/measurement | – | MSR−MSEMSR+k−1MSE |
| Two-way random effects, absolute agreement, single rater/measurement | ICC (2,1) | MSR−MSEMSR+k−1MSE+knMSC−MSE |
| Two-way mixed effects, consistency, single rater/measurement | ICC (3,1) | MSR−MSEMSR+k−1MSE |
| Two-way mixed effects, absolute agreement, single rater/measurement | – | MSR−MSEMSR+k−1MSE+knMSC−MSE |
| One-way random effects, absolute agreement, multiple raters/measurements | ICC (1,k) | MSR−MSWMSR |
| Two-way random effects, consistency, multiple raters/measurements | – | MSR−MSEMSR |
| Two-way random effects, absolute agreement, multiple raters/measurements | ICC (2,k) | MSR−MSEMSR+MSC−MSEn |
| Two-way mixed effects, consistency, multiple raters/measurements | ICC (3,k) | MSR−MSEMSR |
| Two-way mixed effects, absolute agreement, multiple raters/measurements | – | MSR−MSEMSR+MSC−MSEn |
Selection of the correct ICC form for interrater reliability study can be guided by 4 questions: (1) Do we have the same set of raters for all subjects? (2) Do we have a sample of raters randomly selected from a larger population or a specific sample of raters? (3) Are we interested in the reliability of single rater or the mean value of multiple raters? (4) Do we concern about consistency or agreement? The first 2 questions guide the “Model” selection, question 3 guides the “Type” selection, and the last question guides the “Definition” selection.
(A) “Model” Selection
One-Way Random-Effects Model
In this model, each subject is rated by a different set of raters who were randomly chosen from a larger population of possible raters. Practically, this model is rarely used in clinical reliability analysis because majority of the reliability studies typically involve the same set of raters to measure all subjects. An exception would be multicenter studies for which the physical distance between centers prohibits the same set of raters to rate all subjects. Under such circumstance, one set of raters may assess a subgroup of subjects in one center and another set of raters may assess a subgroup of subjects in another center, and hence, 1-way random-effects model should be used in this case.
Two-Way Random-Effects Model
If we randomly select our raters from a larger population of raters with similar characteristics, 2-way random-effects model is the model of choice. In other words, we choose 2-way random-effects model if we plan to generalize our reliability results to any raters who possess the same characteristics as the selected raters in the reliability study. This model is appropriate for evaluating rater-based clinical assessment methods (eg, passive range of motion) that are designed for routine clinical use by any clinicians with specific characteristics (eg, years of experience) as stated in the reliability study.
Two-Way Mixed-Effects Model
We should use the 2-way mixed-effects model if the selected raters are the only raters of interest. With this model, the results only represent the reliability of the specific raters involved in the reliability experiment. They cannot be generalized to other raters even if those raters have similar characteristics as the selected raters in the reliability experiment. As a result, 2-way mixed-effects model is less commonly used in interrater reliability analysis.
(B) “Type” Selection
This selection depends on how the measurement protocol will be conducted in actual application. For instance, if we plan to use the mean value of 3 raters as an assessment basis, the experimental design of the reliability study should involve 3 raters, and the “mean of k raters” type should be selected. Conversely, if we plan to use the measurement from a single rater as the basis of the actual measurement, “single rater” type should be selected even though the reliability experiment involves 2 or more raters.
(C) “Definition” Selection
For both 2-way random- and 2-way mixed-effects models, there are 2 ICC definitions: “absolute agreement” and “consistency.” Selection of the ICC definition depends on whether we consider absolute agreement or consistency between raters to be more important.
Absolute agreement concerns if different raters assign the same score to the same subject. Conversely, consistency definition concerns if raters’ scores to the same group of subjects are correlated in an additive manner.18 Consider an interrater reliability study of 2 raters as an example. In this case, consistency definition concerns the degree to which one rater’s score (y) can be equated to another rater’s score (x) plus a systematic error (c) (ie, y = x + c), whereas absolute agreement concerns about the extent to which y equals x.
How to Select the Correct ICC Form for Test-Retest and Intrarater Reliability Studies
Compared with interrater reliability, the ICC selection process of the test-retest and intrarater reliability is more straightforward. The only question to ask is whether the actual application will be based on a single measurement or the mean of multiple measurements. As for the “Model” selection, Shrout and Fleiss19 suggest that 2-way mixed-effects model is appropriate for testing intrarater reliability with multiple scores from the same rater, as it is not reasonable to generalize one rater’s scores to a larger population of raters. Similarly, 2-way mixed-effects model should also be used in test-retest reliability study because repeated measurements cannot be regarded as randomized samples.2 In addition, absolute agreement definition should always be chosen for both test-retest and intrarater reliability studies because measurements would be meaningless if there is no agreement between repeated measurements.
In summary, selection of an appropriate ICC form for reliability analysis involves identification of the type of reliability study to be conducted, followed by determining the “Model,” “Type,” and “Definition” selection to be used. A diagram streamlining the ICC selection process is shown in Fig 1. It is hoped that this diagram can serve as a quick reference to guide researchers for selecting the correct ICC form for their reliability studies.
Fig 1.
A flowchart showing the selection process of the ICC form based on the experimental design of a reliability study. The process involves the selection of the appropriate model (ie, 1-way random effects, 2-way random effects, or 2-way fixed effects), type (ie, single rater/measurement or the mean of k raters/measurements), and definition of relationship considered to be important (ie, consistency or absolute agreement).
ICC Characteristics
Fig 2 illustrates how different forms of ICC can give different results when applied to the same set of data and how the nature of the data affects ICC estimates of different forms. These calculations revealed some interesting facts about ICC:
- (1) If the data sets are identical, all ICC estimates will equal to 1. (2) Generally speaking, ICC of the “mean of k raters” type is larger than the corresponding “single rater” type. (3) The “absolute agreement” definition generally gives a smaller ICC estimate than the “consistency” definition. (4) One-way random-effects model generally gives a smaller ICC estimate than the 2-way models. (5) For the same ICC definition (eg absolute agreement), ICC estimates of both the 2-way random- and mixed-effects models are the same because they use the same formula to calculate the ICC (Table 3). This brings up an important fact that the difference between 2-way random- and mixed-effects models is not on the calculation but on the experimental design of the reliability study and the interpretation of the results.
Fig 2.
Hypothetical data illustrating how different forms of ICC can give different results when applied to the same set of data and how the nature of the data affects the ICC estimates of different forms.
ICC Interpretation
We have to understand that there are no standard values for acceptable reliability using ICC. A low ICC could not only reflect the low degree of rater or measurement agreement but also relate to the lack of variability among the sampled subjects, the small number of subjects, and the small number of raters being tested.2, 20 As a rule of thumb, researchers should try to obtain at least 30 heterogeneous samples and involve at least 3 raters whenever possible when conducting a reliability study. Under such conditions, we suggest that ICC values less than 0.5 are indicative of poor reliability, values between 0.5 and 0.75 indicate moderate reliability, values between 0.75 and 0.9 indicate good reliability, and values greater than 0.90 indicate excellent reliability.2
Moreover, the ICC estimate obtained from a reliability study is only an expected value of the true ICC. It is logical to determine the level of reliability (ie, poor, moderate, good, and excellent) by testing whether the obtained ICC value significantly exceeds the suggested values mentioned above using statistical inference. This kind of analysis can be readily implemented using SPSS or other statistical software. As part of the reliability analysis, SPSS computes not only an ICC value but also its 95% confidence interval. Table 4 shows a sample output of a reliability analysis from SPSS. In this hypothetical example, the obtained ICC was computed by a single-rating, absolute-agreement, 2-way random-effects model with 3 raters across 30 subjects. Herein, although the obtained ICC value is 0.932 (indicating excellent reliability), its 95% confidence interval ranges between 0.879 and 0.965, meaning that there is 95% chance that the true ICC value lands on any point between 0.879 and 0.965. Therefore, based on statistical inference, it would be more appropriate to conclude the level of reliability to be “good” to “excellent.”
Table 4.
Hypothetical Example Showing Results of ICC Calculation in SPSS Using Single-Rating, Absolute-Agreement, 2-Way Random-Effects Model
| Intraclass Correlation | 95% Confidence Interval | F Test With True Value 0 | |||||
|---|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | Value | _df_1 | _df_2 | Sig | ||
| Single measures | .932 | .879 | .965 | 45.606 | 29 | 58 | .000 |
How to Report ICC
There is currently a lack of standard for reporting ICC in the clinical research community. Given that different forms of ICC involve distinct assumptions in their calculation and will lead to different interpretations, it is imperative for researchers to report detailed information about their ICC estimates. We suggest that the best practice of reporting ICC should include the following items: software information, “Model,” “Type,” and “Definition” selections. In addition, both ICC estimates and their 95% confidence intervals should be reported. For instance, the ICC information could be reported as such:
ICC estimates and their 95% confident intervals were calculated using SPSS statistical package version 23 (SPSS Inc, Chicago, IL) based on a mean-rating (k = 3), absolute-agreement, 2-way mixed-effects model.
We believe that adopting this recommendation will lead to better communication among researchers and clinicians.
Resources for Researchers/Authors
Researchers/authors are recommended to refer to Chapter 5 and 26 of Portney and Watkins2 for a thorough and easy-to-understand discussion about reliability and ICC. For more in-depth information on the topic, researchers may refer to 2 classic articles by McGraw and Wong (1996)18 and Shrout and Fleiss (1979).19 In addition, Nichols (1998)21 provides a succinct description on how to use SPSS for ICC calculation.
Discussion for Readers
Why ICC Matters
Conservative care practitioners regularly perform various measurements. How reliable these measurements are in themselves is clearly essential knowledge to help the practitioners to decide whether a particular measurement is of any value. Without conducting a reliability study personally, this knowledge can only be obtained through scientific literatures. Given that ICC is a widely used reliability index in the literature, an understanding of ICC will help readers to make sense of their own clinical practices and to better interpret published studies.
How to Interpret ICC in Published Studies
Readers should be aware of that interpretation of ICC value is a nontrivial task. Many readers tend to simply rely on reported ICC values to make their assessment. However, we must bear in mind that there are different forms of ICC but that only one form is appropriate for a particular situation. Therefore, before interpreting ICC values reported in an article, it is important for readers to evaluate whether the authors use the correct ICC form in their analyses. This assessment begins with checking whether the authors reported complete information about the ICC form they used in their calculation, and this can be guided by looking up Table 3. As revealed in Table 3, there are 2 different conventions of reporting ICC: (1) McGraw and Wong18 and (2) Shrout and Fleiss.19 Hence, readers should be familiar with their equivalent forms. Indeed, the 6 ICC forms of Shrout and Fleiss are a subset of the 10 ICC forms of McGraw and Wong (Table 3).
If the authors provide incomplete or confusing information about their ICC form, its correctness becomes questionable, and the ICC value must be interpreted with caution. Conversely, if the authors provide complete information about their ICC form, readers may then use Fig 1 as a guideline to evaluate the correctness of the ICC form used in the analysis. If so, the 95% confident interval of the ICC estimate (not the ICC estimate itself) should be used as the basis to evaluate the level of reliability using the following general guideline:
Values less than 0.5 are indicative of poor reliability, values between 0.5 and 0.75 indicate moderate reliability, values between 0.75 and 0.9 indicate good reliability, and values greater than 0.90 indicate excellent reliability.
For instance, according to the above guideline, if the 95% confident interval of an ICC estimate is 0.83-0.94, the level of reliability can be regarded as “good’ to “excellent.” It is because, in this case, the true ICC value supposes to land on any point between 0.83 and 0.94. However, let us say that the 95% confident interval of an ICC estimate is 0.92-0.99; the level of reliability should be regarded as “excellent” because even in the worst case scenario, the true ICC is still greater than 0.9.
Fig 3 summarizes the ICC interpretation process. Now let us use it to evaluate a hypothetical example.
Fig 3.
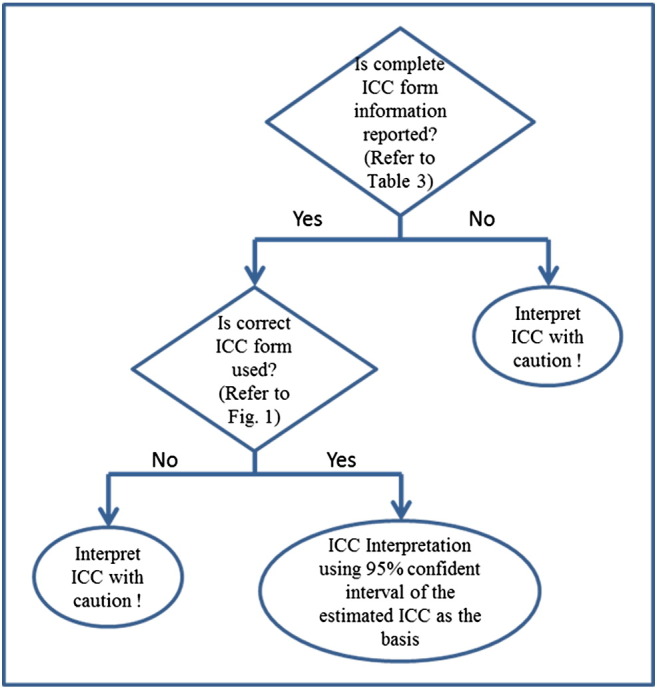
A flowchart showing readers how to interpret ICC in published studies. Values less than 0.5 are indicative of poor reliability, values between 0.5 and 0.75 indicate moderate reliability, values between 0.75 and 0.9 indicate good reliability, and values greater than 0.90 indicate excellent reliability.
Case Description
A clinical researcher developed a new ultrasonography-based method to quantify scoliotic deformity. Before he applied the new method for his routine clinical practice, he conducted a reliability study to evaluate its test-retest reliability. He recruited 35 scoliosis patients with a wide range of deformities from a children’s hospital and used his new method to measure their scoliotic deformity. Measurements were repeated 3 times for each patient. He analyzed his data using a single-measurement, absolute-agreement, 2-way mixed-effects model and reported his ICC results in a peer-reviewed journal as ICC = 0.78 with 95% confident interval = 0.72-0.84. Based on the ICC results, he concluded that the test-retest reliability of his new method is “moderate” to “good.”
Case Discussion
To evaluate whether the researcher’s conclusion is valid or not, we begin with asking whether the researcher provided complete ICC form information (Fig 3, question 1). As revealed in the case description, the researcher used a single-measurement, absolute-agreement, 2-way mixed-effects model for his ICC calculation, which is one of the 10 ICC forms according to Table 3. Because the answer to question 1 is “yes,” we proceed to ask whether the researcher selected the correct ICC form for this study (question 2). According to Fig 1, we conclude that the single-measurement, absolute-agreement, 2-way mixed-effects model is the model of choice for test-retest reliability study, and hence, we can move on to interpret the level of reliability based on the reported 95% confidence interval of the estimated ICC, which is “moderate” to “good.” We therefore conclude that the researcher’s conclusion is a valid one.
Conclusion
In summary, ICC is a reliability index that reflects both degree of correlation and agreement between measurements. It has been widely used in conservative care medicine to evaluate interrater, test-retest, and intrarater reliability of numerical or continuous measurements. Given that there are 10 different forms of ICC and each form involves distinct assumptions in their calculations and will lead to different interpretations, it is important for researchers and readers to understand the principles of selecting an appropriate ICC form. Because the ICC estimate obtained from a reliability study is only an expected value of the true ICC, it is more appropriate to evaluate the level of reliability based on the 95% confident interval of the ICC estimate, not the ICC estimate itself.
Funding Sources and Conflicts of Interest
No funding sources or conflicts of interest were reported for this study.
References
- 1.Daly LE, Bourke GJ. Blackwell Science Ltd; Oxford: 2000. Interpretation and use of medical statistics. [Google Scholar]
- 2.Portney LG, Watkins MP. Prentice Hall; New Jersey: 2000. Foundations of clinical research: applications to practice. [Google Scholar]
- 3.Bruton A, Conway JH, Holgate ST. Reliability: what is it, and how is it measured? Physiotherapy. 2000;86:94–99. [Google Scholar]
- 4.Ebel RL. Estimation of the reliabilty of ratings. Psychometrika. 1951;16:407–424. [Google Scholar]
- 5.Bartko JJ. The intraclass correlation coefficient as a measure of reliability. Psychol Rep. 1966;19:3–11. doi: 10.2466/pr0.1966.19.1.3. [DOI] [PubMed] [Google Scholar]
- 6.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1:307–310. [PubMed] [Google Scholar]
- 7.Brown BW, Jr., Lucero RJ, Foss AB. A situation where the Pearson correlation coefficient leads to erroneous assessment of reliability. J Clin Psychol. 1962;18:95–97. doi: 10.1002/1097-4679(196201)18:1<95::aid-jclp2270180131>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- 8.Hopkins WG. Measures of reliability in sports medicine and science. Sports Med. 2000;30:1–15. doi: 10.2165/00007256-200030010-00001. [DOI] [PubMed] [Google Scholar]
- 9.Fisher RA. Oliver and Boyd; Edinburgh: 1954. Statistical methods for research workers. [Google Scholar]
- 10.Cramer GD, Cantu JA, Pocius JD, Cambron JA, McKinnis RA. Reliability of zygapophysial joint space measurements made from magnetic resonance imaging scans of acute low back pain subjects: comparison of 2 statistical methods. J Manipulative Physiol Ther. 2010;33:220–225. doi: 10.1016/j.jmpt.2010.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Owens EF, Jr., Hart JF, Donofrio JJ, Haralambous J, Mierzejewski E. Paraspinal skin temperature patterns: an interexaminer and intraexaminer reliability study. J Manipulative Physiol Ther. 2004;27:155–159. doi: 10.1016/j.jmpt.2003.12.019. [DOI] [PubMed] [Google Scholar]
- 12.Koo TK, Cohen JH, Zheng Y. A mechano-acoustic indentor system for in vivo measurement of nonlinear elastic properties of soft tissue. J Manipulative Physiol Ther. 2011;34:584–593. doi: 10.1016/j.jmpt.2011.05.009. [DOI] [PubMed] [Google Scholar]
- 13.Clare HA, Adams R, Maher CG. Reliability of detection of lumbar lateral shift. J Manipulative Physiol Ther. 2003;26:476–480. doi: 10.1016/S0161-4754(03)00104-0. [DOI] [PubMed] [Google Scholar]
- 14.Houweling T, Bolton J, Newell D. Comparison of two methods of collecting healthcare usage data in chiropractic clinics: patient-report versus documentation in patient files. Chiropr Man Ther. 2014;22:32. doi: 10.1186/s12998-014-0032-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Battaglia PJ, Maeda Y, Welk A, Hough B, Kettner N. Reliability of the Goutallier classification in quantifying muscle fatty degeneration in the lumbar multifidus using magnetic resonance imaging. J Manipulative Physiol Ther. 2014;37:190–197. doi: 10.1016/j.jmpt.2013.12.010. [DOI] [PubMed] [Google Scholar]
- 16.Leach RA, Parker PL, Veal PS. PulStar differential compliance spinal instrument: a randomized interexaminer and intraexaminer reliability study. J Manipulative Physiol Ther. 2003;26:493–501. doi: 10.1016/S0161-4754(03)00106-4. [DOI] [PubMed] [Google Scholar]
- 17.Russell BS, Muhlenkamp KA, Hoiriis KT, Desimone CM. Measurement of lumbar lordosis in static standing posture with and without high-heeled shoes. J Chiropr Med. 2012;11:145–153. doi: 10.1016/j.jcm.2012.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.McGraw KO, Wong SP. Forming inferences about some intraclass correlation coefficients. Psychol Methods. 1996;1:30–46. [Google Scholar]
- 19.Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychol Bull. 1979;86:420–428. doi: 10.1037//0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]
- 20.Lee KM, Lee J, Chung CY. Pitfalls and important issues in testing reliability using intraclass correlation coefficients in orthopaedic research. Clin Orthop Surg. 2012;4:149–155. doi: 10.4055/cios.2012.4.2.149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nichols DP. Choosing an intraclass correlation coefficient. http://www.ats.ucla.edu/stat/spss/library/whichicc.htm From.