Distribution of the product confidence limits for the indirect effect: program PRODCLIN - PubMed (original) (raw)

Distribution of the product confidence limits for the indirect effect: program PRODCLIN

David P MacKinnon et al. Behav Res Methods. 2007 Aug.

Abstract

This article describes a program, PRODCLIN (distribution of the PRODuct Confidence Limits for INdirect effects), written for SAS, SPSS, and R, that computes confidence limits for the product of two normal random variables. The program is important because it can be used to obtain more accurate confidence limits for the indirect effect, as demonstrated in several recent articles (MacKinnon, Lockwood, & Williams, 2004; Pituch, Whittaker, & Stapleton, 2005). Tests of the significance of and confidence limits for indirect effects based on the distribution of the product method have more accurate Type I error rates and more power than other, more commonly used tests. Values for the two paths involved in the indirect effect and their standard errors are entered in the PRODCLIN program, and distribution of the product confidence limits are computed. Several examples are used to illustrate the PRODCLIN program. The PRODCLIN programs in rich text format may be downloaded from www.psychonomic.org/archive.

PubMed Disclaimer

Figures

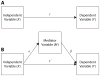
Figure 1

The indirect effect model.

Figure 2

Flow chart for the PRODCLIN program SAS.

Similar articles

• RMediation: an R package for mediation analysis confidence intervals.
  Tofighi D, MacKinnon DP. Tofighi D, et al. Behav Res Methods. 2011 Sep;43(3):692-700. doi: 10.3758/s13428-011-0076-x. Behav Res Methods. 2011. PMID: 21487904 Free PMC article.
• SPSS and SAS procedures for estimating indirect effects in simple mediation models.
  Preacher KJ, Hayes AF. Preacher KJ, et al. Behav Res Methods Instrum Comput. 2004 Nov;36(4):717-31. doi: 10.3758/bf03206553. Behav Res Methods Instrum Comput. 2004. PMID: 15641418
• Confidence Limits for the Indirect Effect: Distribution of the Product and Resampling Methods.
  Mackinnon DP, Lockwood CM, Williams J. Mackinnon DP, et al. Multivariate Behav Res. 2004 Jan 1;39(1):99. doi: 10.1207/s15327906mbr3901_4. Multivariate Behav Res. 2004. PMID: 20157642 Free PMC article.
• Sample size planning for statistical power and accuracy in parameter estimation.
  Maxwell SE, Kelley K, Rausch JR. Maxwell SE, et al. Annu Rev Psychol. 2008;59:537-63. doi: 10.1146/annurev.psych.59.103006.093735. Annu Rev Psychol. 2008. PMID: 17937603 Review.
• A Review of the Use of Confidence Intervals for Bland-Altman Limits of Agreement in Optometry and Vision Science.
  Carkeet A. Carkeet A. Optom Vis Sci. 2020 Jan;97(1):3-8. doi: 10.1097/OPX.0000000000001465. Optom Vis Sci. 2020. PMID: 31895271 Review.

Cited by

• The genetic precursors and the advantageous and disadvantageous sequelae of inhibited temperament: an evolutionary perspective.
  Davies PT, Cicchetti D, Hentges RF, Sturge-Apple ML. Davies PT, et al. Dev Psychol. 2013 Dec;49(12):2285-300. doi: 10.1037/a0032312. Epub 2013 Mar 25. Dev Psychol. 2013. PMID: 23527493 Free PMC article.
• Power and sample size calculations for evaluating mediation effects in longitudinal studies.
  Wang C, Xue X. Wang C, et al. Stat Methods Med Res. 2016 Apr;25(2):686-705. doi: 10.1177/0962280212465163. Epub 2012 Dec 6. Stat Methods Med Res. 2016. PMID: 23221975 Free PMC article.
• Posttraumatic stress disorder symptoms mediate the relationship between traumatic experiences and drinking behavior among women attending alcohol-serving venues in a South African township.
  Watt MH, Ranby KW, Meade CS, Sikkema KJ, MacFarlane JC, Skinner D, Pieterse D, Kalichman SC. Watt MH, et al. J Stud Alcohol Drugs. 2012 Jul;73(4):549-58. doi: 10.15288/jsad.2012.73.549. J Stud Alcohol Drugs. 2012. PMID: 22630793 Free PMC article.
• Early subjective response and acquired tolerance as predictors of alcohol use and related problems in a clinical sample.
  Corbin WR, Scott C, Leeman RF, Fucito LM, Toll BA, O'Malley SS. Corbin WR, et al. Alcohol Clin Exp Res. 2013 Mar;37(3):490-7. doi: 10.1111/j.1530-0277.2012.01956.x. Epub 2013 Jan 24. Alcohol Clin Exp Res. 2013. PMID: 23347236 Free PMC article. Clinical Trial.
• Does it get better? A longitudinal analysis of psychological distress and victimization in lesbian, gay, bisexual, transgender, and questioning youth.
  Birkett M, Newcomb ME, Mustanski B. Birkett M, et al. J Adolesc Health. 2015 Mar;56(3):280-5. doi: 10.1016/j.jadohealth.2014.10.275. Epub 2015 Jan 10. J Adolesc Health. 2015. PMID: 25586226 Free PMC article.

References

1. 1. Ajzen I, Fishbein M. Understanding attitudes and predicting social behavior. Englewood Cliffs, NJ: Prentice Hall; 1980.
2. 1. Aroian LA. The probability function of the product of two normally distributed variables. Annals of Mathematical Statistics. 1944;18:265–271.
3. 1. Aroian LA, Taneja VS, Cornwell LW. Mathematical forms of the distribution of the product of two normal variables. Communications in Statistics: Theory & Methods. 1978;7:165–172.
4. 1. Bentler P. EQS for Windows (Version 5.6). [Computer program] Encino, CA: Multivariate Software, Inc; 1997.
5. 1. Bishop YMM, Fienberg SE, Holland PW. Discrete multivariate analysis: Theory and practice. Cambridge, MA: MIT Press; 1975.

Publication types

MeSH terms

LinkOut - more resources

• Full Text Sources

  • Europe PubMed Central
  • PubMed Central