C++ Mathematical Expression Library (ExprTk) (original) (raw)
Description
The C++ Mathematical Expression Toolkit Library (ExprTk) is a versatile, simple to use, easy to integrate and extremely efficient runtime mathematical expression parser and evaluation engine. ExprTk supports numerous forms of functional, logical and vector processing semantics and is very easily extendible.
Capabilities
The ExprTk library has the following capabilities:
- Mathematical operators (+, -, *, /, %, ^)
- Equalities & Inequalities (=, ==, <>, !=, <, <=, >, >=)
- Assignment (:=, +=, -=, *=, /=, %=)
- Logical operators (and, nand, nor, not, or, xor, xnor, mand, mor)
- Functions (abs, avg, ceil, clamp, erf, erfc, exp, expm1, floor, frac, hypot, iclamp, inrange, log, log10, log1p, log2, logn, max, min, mod, mul, ncdf, pow, root, round, roundn, sgn, sqrt, sum, swap, trunc, equal, not_equal)
- Trigonometry (acos, acosh, asin, asinh, atan, atan2, atanh, cos, cosh, cot, csc, sec, sin, sinc, sinh, tan, tanh, deg2rad, rad2deg, deg2grad, grad2deg)
- Control structures (if-then-else, ternary conditional, switch case, return-statement)
- Loop structures (while loop, for loop, repeat until loop, break, continue)
- Optimization of expressions (constant folding, strength reduction, operator coupling, special functions and dead code elimination)
- String operations (equalities, inequalities, logical operators, concatenation and sub-ranges)
- Expression local variables, vectors and strings
- User defined variables, vectors, strings, constants and function support
- Multivariate function composition
- Multiple sequence point and sub expression support
- Runtime checks (vector bounds, string bounds, loop iterations/execution-time bounds, assert statements)
- Compile-time checks (function parameter type checking, compilation and evaluation stackoverflow checks, compilation running time)
- Numerical integration and differentiation
- Vector Processing: BLAS-L1 (axpy, axpby, axpb), all/any-true/false, assign, count, reverse, rotate-left/right, shift-left/right, sort, nth_element, iota, sum, kahan-sum, dot-product, copy, diff, thresholding
- File-IO package (routines include: open, close, read, write, getline, support for binary and text modes)
- Support for various numeric types (float, double, long double, MPFR/GMP)
- Single header implementation, no building required. No external dependencies.
- Completely portable (Compiled and executed upon: x86 x86-64, ARM: 6/7/8/9, Apple: M1/M2/M3/M4, POWER: 6/7/8/9/10, RISC-V: RV64GC/EMSA5/C906/P8700 and AVR32)
Sections
- C++ Mathematical Expression Library License
- Compatibility
- Downloads
- ExprTk Design and General Structure
- Simple Examples
- Extended Examples
- Supplementary Materials
- Benchmarks
- Usage Notes
- Support
C++ Mathematical Expression Library License
 |
Free use of the C++ Mathematical Expression Library is permitted under the guidelines and in accordance with the Open Source MIT License. |
|---|
Compatibility
The C++ Mathematical Expression Library implementation is compatible with the following C++ compilers:
- GNU Compiler Collection (3.5+)
- Clang/LLVM (1.1+)
- Microsoft Visual Studio C++ Compiler (7.1+)
- Intel� C++ Compiler (8.x+)
- AMD Optimizing C++ Compiler (1.2+)
- Nvidia C++ Compiler (19.x+)
- PGI C++ (10.x+)
- IBM XL C/C++ (9.x+)
- Circle C++ (circa: b81c37d2bb227c)
- C++ Builder (XE4+)
Downloads
 C++ Mathematical Expression Library Source Code and Examples
C++ Mathematical Expression Library Source Code and Examples

 ExprTk CMake Solution
ExprTk CMake Solution

 ExprTk MSVC Solutions (2010, 2013, 2015, 2017, 2019, 2022)
ExprTk MSVC Solutions (2010, 2013, 2015, 2017, 2019, 2022)
 ExprTk MPFR Adaptor || ExprTk Real Adaptor || ExprTk Complex Number Adaptor
ExprTk MPFR Adaptor || ExprTk Real Adaptor || ExprTk Complex Number Adaptor
 Documentation / Readme
Documentation / Readme
ExprTk Packages
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|
ExprTk REPL (Read�Evaluate�Print Loop) Binaries:
Example Expressions
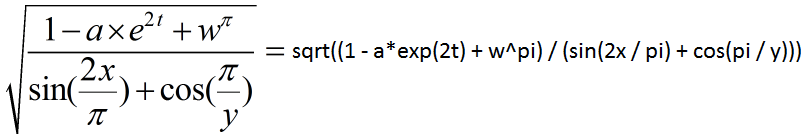
sqrt(1 - (x^2))clamp(-1, sin(2 * pi * x) + cos(y / 2 * pi), +1)sin(2 * x)if (((x + 2) == 3) and ((y + 5) <= 9), 1 + w, 2 / z)inrange(-2, m, +2) == (({-2 <= m} and [m <= +2]) ? 1 : 0)({1 / 1} * [1 / 2] + (1 / 3)) - {1 / 4} ^ [1 / 5] + (1 / 6) -({1 / 7} + [1 / 8] * (1 / 9))a * exp(2 * t) + cz := x + sin(2 * pi / y)2x + 3y + 4z + 5w == 2 * x + 3 * y + 4 * z + 5 * w3(x + y) / 2 + 1 == 3 * (x + y) / 2 + 1(x + y)3 + 1 / 4 == (x + y) * 3 + 1 / 4(x + y)z + 1 / 2 == (x + y) * z + 1 / 2(sin(x / pi)cos(2y) + 1)==(sin(x / pi) * cos(2 * y) + 1)while(x <= 100) { x += 1; }x <= 'abc123' and (y in ('AStr' + 'ing')) or ('1x2y3z' != z)('REX' + x like '*123*') or ('a123b' ilike y)
Basic Design
When compiling and subsequently evaluating an expression with ExprTk, the following three fundamental components will be encountered:
| Component | Purpose / Details |
|---|---|
| exprtk::symbol_table | Holder of external variables, vectors, strings, constants and user defined functions |
| exprtk::parser | Expression factory |
| exprtk::expression | Holder of the AST which is used to evaluate the compiled expression |
Note: NumericType can be any floating point type. This includes but is not limited to: float, double, long double, MPFR or any custom type conforming to an interface compatible with the standard floating point type.
The following diagram depicts each of the above denoted components and how they relate to one another when compiling and evaluating the expression: z := x - (3 * y)

The following example illustrates the events shown in the diagram above. Given an expression string 'z := x - (3 * y)' and three variables_(x, y and z)_, a exprtk::symbol_table is instantiated and the variables are added to it. Then an exprtk::expression is instantiated and the symbol table is registered with the expression instance. Finally an exprtk::parser is instantiated where both the expression object and the string form of the expression are passed to thecompile method of the parser.
If the compilation process is successful the expression instance will now be holding an AST that can be used to evaluate the original expression. Otherwise a compilation error will be raised and diagnostics relating to the error(s) made available via the parser's error reporting interface. The expression in the example will perform a calculation using the variables x and y then proceed to assign the result of the calculation to the variable z.
typedef double T; // numeric type (float, double, mpfr etc...)
typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string expression_string = "z := x - (3 * y)";
T x = T(123.456); T y = T(98.98); T z = T(0.0);
symbol_table_t symbol_table; symbol_table.add_variable("x",x); symbol_table.add_variable("y",y); symbol_table.add_variable("z",z);
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser;
if (!parser.compile(expression_string,expression)) { printf("Compilation error...\n"); return; }
T result = expression.value(); ....
The expression is evaluated by traversing the generated AST in a_postorder_ manner. The order of sub-expression evaluations will be as follows:
Result0 <- (3 * y)z <- (x - Result0)
For a more detailed discussion on the internals of ExprTk and its capabilities it is recommended to have a review of the accompanying:readme.txt
Simple ExprTk Examples
- Example 01 - Simple expression using a single variable (x) with multiple revaluations
- Example 02 - Square-wave form approximation using Fourier series
- Example 03 - Polynomial evaluation with implied multiplications
- Example 04 - Fibonacci sequence via function compositor
- Example 05 - User defined function and expression evaluation
- Example 06 - Vector processing via for-loop
- Example 07 - Truth table generation via symbol referencing and expression evaluation
- Example 08 - Function of function evaluation via compositor
- Example 09 - Prime numbers using various methods
- Example 10 - Square-root via Newton-Raphson method
- Example 11 - Square-wave derived from a large number of harmonics
- Example 12 - Implementation of the Bubble sort algorithm
- Example 13 - Savitzky-Golay digital smoothing filter
- Example 14 - Standard deviation via vector processing methods
- Example 15 - Black-Scholes-Merton option pricing model
- Example 16 - Linear least squares using vector processing methods
- Example 17 - Approximation of Pi (π) via the Monte-Carlo method and vector processing
- Example 18 - File I/O processing demonstration
- Example 19 - User defined var-arg function with vector operations
- Example 20 - Vector processing runtime checks
- Example 21 - Cox, Ross and Rubinstein binomial option pricing model
- Example 22 - Implied volatility of a European option
- Example 23 - 1D Real discrete Fourier transform
- Example 24 - Reverse Polish notation expression evaluator
Renaissance Technologies - Rentec https://www.rentec.com
TGS Management Company - TGS https://www.tgsmc.com
Simple Example 1 - Simple Expression Using A Single Variable With Multiple Revaluations
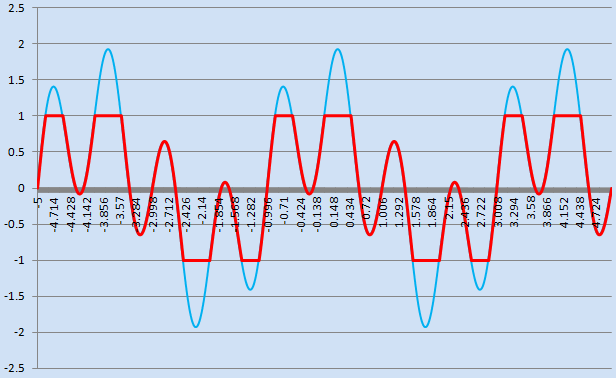
The following is an example where a given single variable function is evaluated within the domain: [-5, +5].

The graph below shows the clamped**_(red)** and non-clamped**(blue)_** versions of the specified function.
The example further demonstrates the common use-case of ExprTk: which is to compile an expression only once, and to then evaluate the compiled expression many times over, and where between each evaluation the expression's dependent variables (eg: x variable) are updated as needed. [source: simple_example_01.cpp]
template void trig_function() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string expression_string = "clamp(-1.0, sin(2 * pi * x) + cos(x / 2 * pi), +1.0)";
T x;
symbol_table_t symbol_table; symbol_table.add_variable("x",x); symbol_table.add_constants();
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(expression_string,expression);
for (x = T(-5); x <= T(+5); x += T(0.001)) { const T y = expression.value(); printf("%19.15f\t%19.15f\n", x, y); } }
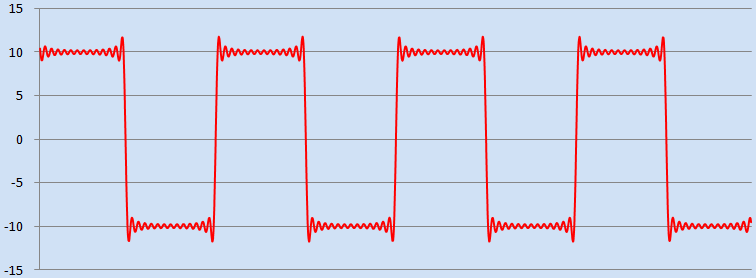
Simple Example 2 - Square-Wave Form Approximation Using Fourier Series
The following example generates a square wave form based on Fourier series accumulations - 14 harmonics. Sigma-approximation is not applied hence Gibbs phenomenon based ringing is observed on the edges of the square, as is demonstrated in the graph below. [source: simple_example_02.cpp]
template void square_wave() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string expression_string = "a *(4 / pi) * " "((1 /1) * sin( 2 * pi * f * t) + (1 /3) * sin( 6 * pi * f * t)+" " (1 /5) * sin(10 * pi * f * t) + (1 /7) * sin(14 * pi * f * t)+" " (1 /9) * sin(18 * pi * f * t) + (1/11) * sin(22 * pi * f * t)+" " (1/13) * sin(26 * pi * f * t) + (1/15) * sin(30 * pi * f * t)+" " (1/17) * sin(34 * pi * f * t) + (1/19) * sin(38 * pi * f * t)+" " (1/21) * sin(42 * pi * f * t) + (1/23) * sin(46 * pi * f * t)+" " (1/25) * sin(50 * pi * f * t) + (1/27) * sin(54 * pi * f * t))";
static const T pi = T(3.141592653589793238462643383279502);
const T f = pi / T(10); const T a = T(10); T t = T(0);
symbol_table_t symbol_table; symbol_table.add_variable("t",t); symbol_table.add_constant("f",f); symbol_table.add_constant("a",a); symbol_table.add_constants();
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(expression_string,expression);
const T delta = (T(4) * pi) / T(1000);
for (t = (T(-2) * pi); t <= (T(+2) * pi); t += delta) { const T result = expression.value(); printf("%19.15f\t%19.15f\n", t, result); } }
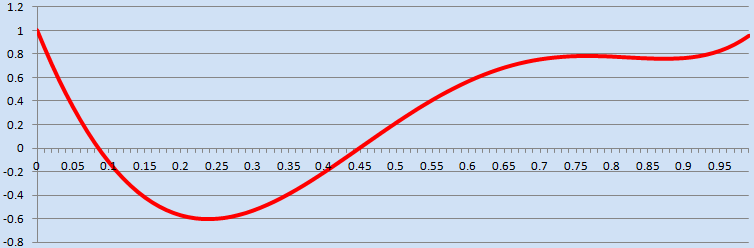
Simple Example 3 - Polynomial Evaluation With Implied Multiplications
The following example evaluates a 5th degree polynomial within the domain [0,1] with a step size of 1/100th. An interesting side note in the expression is how the multiplication of the coefficients to the variable 'x' are implied rather than explicitly defined using the multiplication operator '*' [source: simple_example_03.cpp]
template void polynomial() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string expression_string = "25x^5 - 35x^4 - 15x^3 + 40x^2 - 15x + 1";
const T r0 = T(0); const T r1 = T(1); T x = T(0);
symbol_table_t symbol_table; symbol_table.add_variable("x",x);
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(expression_string,expression);
const T delta = T(1.0 / 100.0);
for (x = r0; x <= r1; x += delta) { printf("%19.15f\t%19.15f\n", x, expression.value()); } }
Simple Example 4 - Fibonacci Sequence Via Function Compositor
The following example generates the first 40 Fibonacci numbers using a simple iterative method. The example demonstrates the use of multiple assignment and sequence points, switch statements, while-loops and composited functions with expression local variables. [source: simple_example_04.cpp]
template void fibonacci() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t; typedef exprtk::function_compositor compositor_t; typedef typename compositor_t::function function_t;
T x = T(0);
compositor_t compositor;
compositor.add( function_t("fibonacci") .var("x") .expression ( " switch " " { " " case x == 0 : 0; " " case x == 1 : 1; " " default : " " { " " var prev := 0; " " var curr := 1; " " while ((x -= 1) > 0) " " { " " var temp := prev; " " prev := curr; " " curr += temp; " " }; " " }; " " } " ));
symbol_table_t& symbol_table = compositor.symbol_table(); symbol_table.add_constants(); symbol_table.add_variable("x",x);
std::string expression_str = "fibonacci(x)";
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(expression_str,expression);
for (std::size_t i = 0; i < 40; ++i) { x = static_cast(i);
const T result = expression.value();
printf("fibonacci(%3d) = %10.0f\n",
static_cast<int>(i),
result);} }
Simple Example 5 - User Defined Function And Expression Evaluation
The following example demonstrates how one can easily register a custom user defined function to be used within expression evaluations. In this example one of the custom functions myfunc takes two parameters as input and returns a result, the other being a free function named myotherfunc which takes three values as input and returns a result. Furthermore the_'myfunc'_ function explicitly enables itself for constant-folding optimisations by indicating it is stateless and has no external side-effects. The upper limit for individual parameters is 20 inputs. If more inputs are required then either the ivararg_function or igeneric_function interfaces can be used, both of which support an unlimited number of input parameters. [source: simple_example_05.cpp]
template struct myfunc final : public exprtk::ifunction { myfunc() : exprtk::ifunction(2) { exprtk::disable_has_side_effects(*this); }
inline T operator()(const T& v1, const T& v2) override { return T(1) + (v1 * v2) / T(3); } };
template inline T myotherfunc(T v0, T v1, T v2) { return std::abs(v0 - v1) * v2; }
template void custom_function() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string expression_string = "myfunc(sin(x / pi), otherfunc(3 * y, x / 2, x * y))";
T x = T(1); T y = T(2);
myfunc mf;
symbol_table_t symbol_table; symbol_table.add_variable("x",x); symbol_table.add_variable("y",y); symbol_table.add_function("myfunc",mf); symbol_table.add_function("otherfunc",myotherfunc); symbol_table.add_constants();
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(expression_string,expression);
T result = expression.value(); printf("Result: %10.5f\n",result); }
Simple Example 6 - Vector Processing Via For-Loop
The following example demonstrates how one can evaluate an expression over multiple vectors. The example evaluates the value of an expression at the ith element of vectors x and y and assigns the value to the ith value of vector z. The example demonstrates the use of vector indexing, the vector 'size' operator and for loops. [source: simple_example_06.cpp]
template void vector_function() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string expression_string = " for (var i := 0; i < min(x[], y[], z[]); i += 1) " " { " " z[i] := 3sin(x[i]) + 2log(y[i]); " " } ";
T x[] = { T(1.1), T(2.2), T(3.3), T(4.4), T(5.5) }; T y[] = { T(1.1), T(2.2), T(3.3), T(4.4), T(5.5) }; T z[] = { T(0.0), T(0.0), T(0.0), T(0.0), T(0.0) };
symbol_table_t symbol_table; symbol_table.add_vector("x",x); symbol_table.add_vector("y",y); symbol_table.add_vector("z",z);
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(expression_string,expression);
expression.value(); }
Simple Example 7 - Truth Table Generation
The following example demonstrates how one can create and later on reference variables via the symbol_table. In the example a simple boolean expression is evaluated so as to determine its truth-table. [source: simple_example_07.cpp]
template void logic() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string expression_string = "not(A and B) or C";
symbol_table_t symbol_table; symbol_table.create_variable("A"); symbol_table.create_variable("B"); symbol_table.create_variable("C");
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(expression_string,expression);
printf(" # | A | B | C | %s\n" "---+---+---+---+-%s\n", expression_string.c_str(), std::string(expression_string.size(),'-').c_str());
for (int i = 0; i < 8; ++i) { symbol_table.get_variable("A")->ref() = T(i & 0x01 ? 1 : 0); symbol_table.get_variable("B")->ref() = T(i & 0x02 ? 1 : 0); symbol_table.get_variable("C")->ref() = T(i & 0x04 ? 1 : 0);
const int result = static_cast<int>(expression.value());
printf(" %d | %d | %d | %d | %d \n",
i,
static_cast<int>(symbol_table.get_variable("A")->value()),
static_cast<int>(symbol_table.get_variable("B")->value()),
static_cast<int>(symbol_table.get_variable("C")->value()),
result);} }
Expected output:
| A | B | C | not(A and B) or C
---+---+---+---+------------------ 0 | 0 | 0 | 0 | 1 1 | 1 | 0 | 0 | 1 2 | 0 | 1 | 0 | 1 3 | 1 | 1 | 0 | 0 4 | 0 | 0 | 1 | 1 5 | 1 | 0 | 1 | 1 6 | 0 | 1 | 1 | 1 7 | 1 | 1 | 1 | 1
Simple Example 8 - Function Of Function Evaluation Via Compositor
The following example demonstrates the function composition capabilities within ExprTk. In the example there are two simple functions defined, an f(x) and a multivariate_g(x,y)_. The function g(x,y) is composed of calls to f(x), the culmination of which is a final expression composed from both functions. Furthermore the example demonstrates how one can extract all errors that were encountered during a failed compilation process. [source: simple_example_08.cpp]
template void composite() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t; typedef exprtk::parser_error::type err_t; typedef exprtk::function_compositor compositor_t; typedef typename compositor_t::function function_t;
T x = T(1); T y = T(2);
compositor_t compositor;
symbol_table_t& symbol_table = compositor.symbol_table(); symbol_table.add_constants(); symbol_table.add_variable("x",x); symbol_table.add_variable("y",y);
compositor.add( function_t("f") // f(x) = sin(x / pi) .var("x") .expression( "sin(x / pi)" ));
compositor.add( function_t("g") // g(x,y) = 3[f(x) + f(y)] .vars("x", "y") .expression( "3*[f(x) + f(y)]" ));
std::string expression_string = "g(1 + f(x), f(y) / 2)";
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser;
if (!parser.compile(expression_string,expression)) { printf("Error: %s\tExpression: %s\n", parser.error().c_str(), expression_string.c_str());
for (std::size_t i = 0; i < parser.error_count(); ++i)
{
const err_t error = parser.get_error(i);
printf("Error: %02d Position: %02d Type: [%14s] Msg: %s\tExpression: %s\n",
static_cast<unsigned int>(i),
static_cast<unsigned int>(error.token.position),
exprtk::parser_error::to_str(error.mode).c_str(),
error.diagnostic.c_str(),
expression_string.c_str());
}
return;}
const T result = expression.value();
printf("%s = %e\n", expression_string.c_str(), result); }
Simple Example 9 - Prime Numbers Using Various Methods
The following example demonstrates the computation of prime numbers via a mixture of recursive composited functions, switch-statement, for-loop and vector processing functionalities. [source: simple_example_09.cpp]
template void primes() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t; typedef exprtk::function_compositor compositor_t; typedef typename compositor_t::function function_t;
T x = T(0);
symbol_table_t symbol_table;
symbol_table.add_constants(); symbol_table.add_variable("x",x);
compositor_t compositor(symbol_table);
//Mode 1 - if statement based compositor.add( function_t("is_prime_impl1") .vars("x", "y") .expression ( " if (y == 1,true, " " if (0 == (x % y),false, " " is_prime_impl1(x,y - 1))) " ));
compositor.add( function_t("is_prime1") .var("x") .expression ( " if (frac(x) != 0) " " return [false]; " " else if (x <= 0) " " return [false]; " " else " " is_prime_impl1(x,min(x - 1,trunc(sqrt(x)) + 1)); " ));
//Mode 2 - switch statement based compositor.add( function_t("is_prime_impl2") .vars("x", "y") .expression ( " switch " " { " " case y == 1 : true; " " case (x % y) == 0 : false; " " default : is_prime_impl2(x,y - 1); " " } " ));
compositor.add( function_t("is_prime2") .var("x") .expression ( " switch " " { " " case x <= 0 : false; " " case frac(x) != 0 : false; " " default : is_prime_impl2(x,min(x - 1,trunc(sqrt(x)) + 1)); " " } " ));
//Mode 3 - switch statement and for-loop based compositor.add( function_t("is_prime3") .var("x") .expression ( " switch " " { " " case x <= 1 : return [false]; " " case frac(x) != 0 : return [false]; " " case x == 2 : return [true ]; " " }; " " " " var prime_lut[27] := " " { " " 2, 3, 5, 7, 11, 13, 17, 19, 23, " " 29, 31, 37, 41, 43, 47, 53, 59, 61, " " 67, 71, 73, 79, 83, 89, 97, 101, 103 " " }; " " " " var upper_bound := min(x - 1, trunc(sqrt(x)) + 1); " " " " for (var i := 0; i < prime_lut[]; i += 1) " " { " " if (prime_lut[i] >= upper_bound) " " return [true]; " " else if ((x % prime_lut[i]) == 0) " " return [false]; " " }; " " " " var lower_bound := prime_lut[prime_lut[] - 1] + 2; " " " " for (var i := lower_bound; i < upper_bound; i += 2) " " { " " if ((x % i) == 0) " " { " " return [false]; " " } " " }; " " " " return [true]; " ));
std::string expression_str1 = "is_prime1(x)"; std::string expression_str2 = "is_prime2(x)"; std::string expression_str3 = "is_prime3(x)";
expression_t expression1; expression_t expression2; expression_t expression3; expression1.register_symbol_table(symbol_table); expression2.register_symbol_table(symbol_table); expression3.register_symbol_table(symbol_table);
parser_t parser;
parser.compile(expression_str1, expression1); parser.compile(expression_str2, expression2); parser.compile(expression_str3, expression3);
for (std::size_t i = 0; i < 15000; ++i) { x = static_cast(i);
const T result1 = expression1.value();
const T result2 = expression2.value();
const T result3 = expression3.value();
const bool results_concur = (result1 == result2) &&
(result1 == result3) ;
printf("%03d Result1: %c Result2: %c Result3: %c "
"Results Concur: %c\n",
static_cast<unsigned int>(i),
(result1 == T(1)) ? 'T' : 'F',
(result2 == T(1)) ? 'T' : 'F',
(result3 == T(1)) ? 'T' : 'F',
(results_concur) ? 'T' : 'F');} }
Simple Example 10 - Square-Root Via Newton-Raphson Method
The following example is an implementation of the Newton�Raphson method for computing the approximate of the square root of a real number. The example below demonstrates the use of multiple sub-expressions, sequence points, switch statements, expression local variables, function compositor and the repeat until loop. [source: simple_example_10.cpp]
template void newton_sqrt() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t; typedef exprtk::function_compositor compositor_t; typedef typename compositor_t::function function_t;
T x = T(0);
symbol_table_t symbol_table;
symbol_table.add_constants(); symbol_table.add_variable("x",x);
compositor_t compositor(symbol_table);
compositor.add( function_t("newton_sqrt") .var("x") .expression ( " switch " " { " " case x < 0 : null; " " case x == 0 : 0; " " case x == 1 : 1; " " default: " " { " " var z := 100; " " var sqrt_x := x / 2; " " repeat " " if (equal(sqrt_x^2, x)) " " break[sqrt_x]; " " else " " sqrt_x := (1 / 2) * (sqrt_x + (x / sqrt_x)); " " until ((z -= 1) <= 0); " " }; " " } " ));
const std::string expression_str = "newton_sqrt(x)";
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(expression_str,expression);
for (std::size_t i = 0; i < 1000; ++i) { x = static_cast(i);
const T result = expression.value();
const T real = std::sqrt(x);
const T error = std::abs(result - real);
printf("sqrt(%03d) - Result: %15.13f\tReal: %15.13f\tError: %18.16f\n",
static_cast<unsigned int>(i),
result,
real,
error);} }
Simple Example 11 - Square-Wave Derived From A Large Number Of Harmonics
The following is similar to Example 2. However in this example, the square wave form is generated using 1000 harmonics. The example demonstrates the use of for-loops, implied multiplications, expression local variables and addition/multiplication assignment operators. [source: simple_example_11.cpp]
template void square_wave2() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string wave_program = " var r := 0; " " " " for (var i := 0; i < 1000; i += 1) " " { " " r += (1 / (2i + 1)) * sin((4i + 2) * pi * f * t); " " }; " " " " r *= a * (4 / pi); ";
static const T pi = T(3.141592653589793238462643383279502);
T f = pi / T(10); T t = T(0); T a = T(10);
symbol_table_t symbol_table; symbol_table.add_variable("f",f); symbol_table.add_variable("t",t); symbol_table.add_variable("a",a); symbol_table.add_constants();
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(wave_program,expression);
const T delta = (T(4) * pi) / T(1000);
for (t = (T(-2) * pi); t <= (T(+2) * pi); t += delta) { const T result = expression.value(); printf("%19.15f\t%19.15f\n", t, result); } }
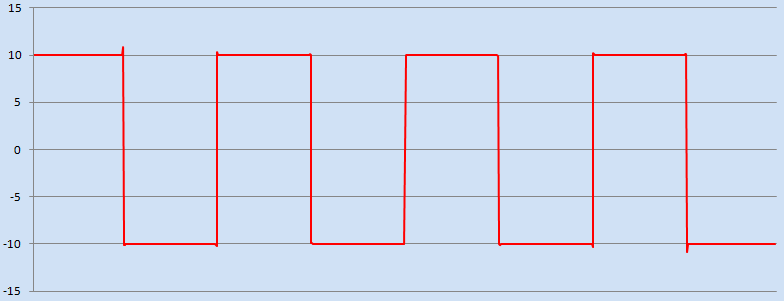
Simple Example 12 - Implementation Of The Bubble Sort Algorithm
The following is an example of the 'venerable' Bubble Sort algorithm. The example demonstrates functionality such as vector elements, repeat-until loop, nested for-loop, expression local variables and the swap operator. [source: simple_example_12.cpp]
template void bubble_sort() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string bubblesort_program = " var upper_bound := v[]; " " " " repeat " " var new_upper_bound := 0; " " " " for (var i := 1; i < upper_bound; i += 1) " " { " " if (v[i - 1] > v[i]) " " { " " v[i - 1] <=> v[i]; " " new_upper_bound := i; " " }; " " }; " " " " upper_bound := new_upper_bound; " " " " until (upper_bound <= 1); ";
T v[] = { T(9.1), T(2.2), T(1.3), T(5.4), T(7.5), T(4.6), T(3.7) };
symbol_table_t symbol_table; symbol_table.add_vector("v",v);
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(bubblesort_program,expression);
expression.value(); }
Simple Example 13 - Savitzky-Golay Digital Smoothing Filter
The following is an example implementation of the Savitzky-Golay smoothing filter. A periodic signal with Additive White noise is generated (v_in), the Savitzky-Golay filter is then applied to the noisy signal and output to the vector v_out. The graph below denotes the noisy and smoothed signals in blue and red respectively. The example demonstrates the use of user defined vectors, expression local vectors and variables, nested for-loops, conditional statements and the vector size operator. [source: simple_example_13.cpp]
template void savitzky_golay_filter() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string sgfilter_program = " var weight[9] := " " { " " -21, 14, 39, " " 54, 59, 54, " " 39, 14, -21 " " }; " " " " if (v_in[] >= weight[]) " " { " " const var lower_bound := trunc(weight[] / 2); " " const var upper_bound := v_in[] - lower_bound; " " " " v_out := 0; " " " " for (var i := lower_bound; i < upper_bound; i += 1) " " { " " for (var j := -lower_bound; j <= lower_bound; j += 1) " " { " " v_out[i] += weight[j + lower_bound] * v_in[i + j]; " " }; " " }; " " " " v_out /= sum(weight); " " } ";
const std::size_t n = 1024;
std::vector v_in; std::vector v_out;
const T pi = T(3.141592653589793238462643383279502);
srand(static_cast(time(0)));
// Generate a signal with noise. for (T t = T(-5); t <= T(+5); t += T(10.0 / n)) { const T noise = T(0.5 * (rand() / (RAND_MAX + 1.0) - 0.5)); v_in.push_back(sin(2.0 * pi * t) + noise); }
v_out.resize(v_in.size());
symbol_table_t symbol_table; symbol_table.add_vector("v_in" , v_in ); symbol_table.add_vector("v_out", v_out);
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(sgfilter_program,expression);
expression.value();
for (std::size_t i = 0; i < v_out.size(); ++i) { printf("%10.6f\t%10.6f\n", v_in[i], v_out[i]); } }

Simple Example 14 - Standard Deviation Via Vector Processing Methods
The following example calculates the population Standard Deviation of a vector x comprised of values in the range [1,25]. The example demonstrates the vector processing capabilities of ExprTk, such as the definition and initialisation of expression local vectors, unary-operator and aggregator functions over vectors, scalar-vector arithmetic and the vector size operator. [source: simple_example_14.cpp]
template void stddev_example() { typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string stddev_program = " var x[25] := { " " 1, 2, 3, 4, 5, " " 6, 7, 8, 9, 10, " " 11, 12, 13, 14, 15, " " 16, 17, 18, 19, 20, " " 21, 22, 23, 24, 25 " " }; " " " " sqrt(sum([x - avg(x)]^2) / x[]) ";
expression_t expression;
parser_t parser; parser.compile(stddev_program,expression);
T stddev = expression.value();
printf("stddev(1..25) = %10.6f\n",stddev); }
Simple Example 15 - Black-Scholes-Merton Option Pricing Model
The following example calculates the price of European Call and Put options using the Black-Scholes-Merton option pricing model, and confirms the prices are arbitrage free by computing thePut-Call parity. The example demonstrates the use of user defined and expression local variables, user defined numeric constants, conditional statements, string comparisons and arithmetic functionality. [source: simple_example_15.cpp]
template void black_scholes_merton_model() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string bsm_model_program = " var d1 := (log(s / k) + (r + v^2 / 2) * t) / (v * sqrt(t)); " " var d2 := d1 - v * sqrt(t); " " " " if (callput_flag == 'call') " " s * ncdf(d1) - k * e^(-r * t) * ncdf(d2); " " else if (callput_flag == 'put') " " k * e^(-r * t) * ncdf(-d2) - s * ncdf(-d1); " " ";
T s = T(60.00); // Spot / Stock / Underlying / Base price T k = T(65.00); // Strike price T v = T( 0.30); // Volatility T t = T( 0.25); // Years to maturity T r = T( 0.08); // Risk free rate
std::string callput_flag;
static const T e = exprtk::details::numeric::constant::e;
symbol_table_t symbol_table; symbol_table.add_variable("s",s); symbol_table.add_variable("k",k); symbol_table.add_variable("t",t); symbol_table.add_variable("r",r); symbol_table.add_variable("v",v); symbol_table.add_constant("e",e); symbol_table.add_stringvar("callput_flag",callput_flag);
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(bsm_model_program,expression);
callput_flag = "call";
const T bsm_call_option_price = expression.value();
callput_flag = "put";
const T bsm_put_option_price = expression.value();
printf("BSM(call, %5.3f, %5.3f, %5.3f, %5.3f, %5.3f) = %10.6f\n", s, k, t, r, v, bsm_call_option_price);
printf("BSM(put , %5.3f, %5.3f, %5.3f, %5.3f, %5.3f) = %10.6f\n", s, k, t, r, v, bsm_put_option_price);
const T put_call_parity_diff = (bsm_call_option_price - bsm_put_option_price) - (s - k * std::exp(-r * t));
printf("Put-Call parity difference: %20.17f\n", put_call_parity_diff); }
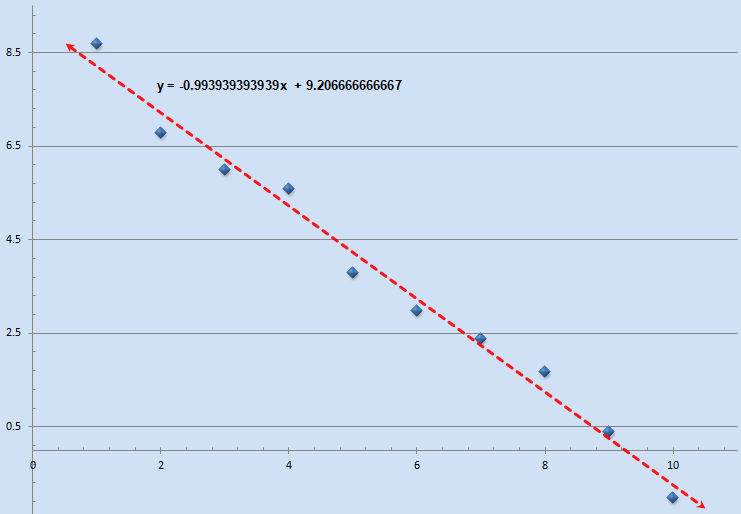
Simple Example 16 - Linear Least Squares Using Vector Processing Methods
The following example attempts to compute a linear fit for a set of 2D data points utilizing the Linear Least Squares method. The data points are comprised of two vectors named x and y plotted as blue on the chart, the result being a linear equation in the form of y = β x + α which is depicted in red. The example demonstrates the use of user defined vectors, vector operations and aggregators and conditional statements. [source: simple_example_16.cpp]
template void linear_least_squares() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string linear_least_squares_program = " if (x[] == y[]) " " { " " var mean_x := avg(x); " " var mean_y := avg(y); " " " " beta := sum((x - mean_x) * (y - mean_y)) / " " sum((x - mean_x)^2); " " " " alpha := mean_y - beta * mean_x; " " " " rmse := sqrt(sum((beta * x + alpha - y)^2) / y[]); " " } " " else " " { " " alpha := null; " " beta := null; " " rmse := null; " " } ";
T x[] = {T( 1), T( 2), T(3), T( 4), T( 5), T(6), T( 7), T( 8), T( 9), T(10)}; T y[] = {T(8.7), T(6.8), T(6), T(5.6), T(3.8), T(3), T(2.4), T(1.7), T(0.4), T(-1)};
T alpha = T(0); T beta = T(0); T rmse = T(0);
symbol_table_t symbol_table; symbol_table.add_variable("alpha", alpha); symbol_table.add_variable("beta" , beta ); symbol_table.add_variable("rmse" , rmse ); symbol_table.add_vector ("x" , x ); symbol_table.add_vector ("y" , y );
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; if (!parser.compile(linear_least_squares_program,expression)) { printf("error: %s\n",parser.error().c_str()); return; }
expression.value();
printf("alpha: %15.12f\n", alpha); printf("beta: %15.12f\n", beta ); printf("rmse: %15.12f\n", rmse ); printf("y = %15.12fx + %15.12f\n", beta, alpha); }
Simple Example 17 - Approximation Of Pi (π) via The Monte-Carlo Method
The following example will compute an approximate value forπ using theMonte-Carlo method. The example demonstrates the use of vector inequality operations, vector initialisation via expressions, the vector size operator, the summation aggregator and user defined functions for generating a uniformly distributed random value in the range [0,1). [source: simple_example_17.cpp]
template struct rnd_01 final : public exprtk::ifunction { using exprtk::ifunction::operator();
rnd_01() : exprtk::ifunction(0) { ::srand(static_cast(time(NULL))); }
inline T operator()() override { // Note: Do not use this in production // Result is in the interval [0,1) return T(::rand() / T(RAND_MAX + 1.0)); } };
template void monte_carlo_pi() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string monte_carlo_pi_program = " var samples[2 * 10^8] := [(rnd_01^2 + rnd_01^2) <= 1]; " " 4 * sum(samples) / samples[]; ";
rnd_01 rnd01;
symbol_table_t symbol_table; symbol_table.add_function("rnd_01",rnd01);
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(monte_carlo_pi_program,expression);
const T approximate_pi = expression.value();
const T real_pi = T(3.141592653589793238462643383279502); // or close enough...
printf("pi ~ %20.17f\terror: %20.17f\n", approximate_pi, std::abs(real_pi - approximate_pi)); }
Simple Example 18 - File I/O Processing Demonstration
The following example will open a file named 'file.txt' in write mode, and write to the file a piece of text ten times, then finally close the file. The following example demonstrates the ExprTk file I/O package capabilities, handle manipulations, the null type, local string variables, if-else statements and for-loops. [source: simple_example_18.cpp]
template void file_io() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string fileio_program = " var file_name := 'file.txt'; " " var stream := null; " " " " if (stream := open(file_name,'w')) " " println('Successfully opened file: ' + file_name); " " else " " { " " println('Failed to open file: ' + file_name); " " return [false]; " " }; " " " " var s := 'Hello world...'; " " " " for (var i := 0; i < 10; i += 1) " " { " " write(stream,s); " " }; " " " " if (close(stream)) " " println('Sucessfully closed file: ' + file_name); " " else " " { " " println('Failed to close file: ' + file_name); " " return [false]; " " } ";
exprtk::rtl::io::file::package fileio_package; exprtk::rtl::io::println println;
symbol_table_t symbol_table; symbol_table.add_function("println",println); symbol_table.add_package (fileio_package );
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(fileio_program,expression);
printf("Result %10.3f\n",expression.value()); }
Simple Example 19 - User Defined Var-Arg Function With Vector Operations
The following example illustrates a var-arg igeneric_function definition that can handle two specific overloads. The first being a vector only, the second being a vector and range (using two scalars) input set. The function when invoked will populate the input vector over the defined range with uniformly distributed pseudo-random values in the range [0,1). The example expression takes a signal vector, then proceeds to add a noise vector to the signal, resulting in a 'noisy-signal'. Furthermore the resulting noisy signal's average as well as its element-wise form is printed to stdout using a for-loop. [source: simple_example_19.cpp]
template class randu : public exprtk::igeneric_function { public:
typedef typename exprtk::igeneric_function igfun_t; typedef typename igfun_t::parameter_list_t parameter_list_t; typedef typename igfun_t::generic_type generic_type; typedef typename generic_type::vector_view vector_t;
using exprtk::igeneric_function::operator();
randu() : exprtk::igeneric_function("V|VTT") /* Overloads: 0. V - vector 1. VTT - vector, r0, r1 */ { ::srand(static_cast(time(NULL))); }
inline T operator()(const std::size_t& ps_index, parameter_list_t parameters) { vector_t v(parameters[0]);
std::size_t r0 = 0;
std::size_t r1 = v.size() - 1;
using namespace exprtk::rtl::vecops::helper;
if (
(1 == ps_index) &&
!load_vector_range<T>::process(parameters, r0, r1, 1, 2, 0)
)
return T(0);
for (std::size_t i = r0; i <= r1; ++i)
{
v[i] = rnd();
}
return T(1);}
private:
inline T rnd() { // Note: Do not use this in production // Result is in the interval [0,1) return T(::rand() / T(RAND_MAX + 1.0)); } };
template void vector_randu() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string vecrandu_program = " var noise[6] := [0]; " " " " if (randu(noise, 0, 5) == false) " " { " " println('Failed to generate noise'); " " return [false]; " " }; " " " " var noisy[noise[]] := signal + (noise - 1/2); " " " " for (var i := 0; i < noisy[]; i += 1) " " { " " println('noisy[',i,'] = ', noisy[i]); " " }; " " " " println('avg: ', avg(noisy)); " " ";
T signal[] = { T(1.1), T(2.2), T(3.3), T(4.4), T(5.5), T(6.6), T(7.7) };
exprtk::rtl::io::println println; randu randu;
symbol_table_t symbol_table; symbol_table.add_vector ("signal" , signal ); symbol_table.add_function("println", println); symbol_table.add_function("randu" , randu );
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(vecrandu_program,expression);
expression.value(); }
Simple Example 20 - Vector Processing Runtime Checks
ExprTk provides the ability to catch and handle, at runtime, vector access and processing violations. This is achieved by initially registering with the parser a Vector Access Runtime Check (VARTC) handler that subsequently is used to inject runtime checks into vector processing statements. The following example demonstrates how a simple custom VARTC can be defined and registered with a parser. The expression when evaluated will trigger an access violation, the handler will attempt to determine which vector the violation occurred on, and then print pertinent information to stdout. [source: simple_example_20.cpp]
struct vector_access_rtc : public exprtk::vector_access_runtime_check { typedef std::map<void*, std::string> map_t; map_t vector_map;
bool handle_runtime_violation(violation_context& context) { const map_t::iterator itr = vector_map.find(static_cast<void*>(context.base_ptr)); const std::string vector_name = (itr != vector_map.end()) ? itr->second : "Unknown" ;
printf("Runtime vector access violation\n"
"Vector: %s base: %p end: %p access: %p typesize: %d\n",
vector_name.c_str(),
context.base_ptr ,
context.end_ptr ,
context.access_ptr ,
static_cast<unsigned int>(context.type_size));
throw std::runtime_error
("Runtime vector access violation. Vector: " + vector_name);
return false;} };
template void vector_overflow_example() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string expression_str = " for (var i := 0; i < max(v0[],v1[]); i += 1) " " { " " v0[i] := (2 * v0[i]) + (v1[i] / 3); " " } ";
T v0[5 ] = { 0, 1, 2, 3, 4 }; T v1[10] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 };
vector_access_rtc vec_rtc;
vec_rtc.vector_map[v0] = "v0"; vec_rtc.vector_map[v1] = "v1";
symbol_table_t symbol_table; expression_t expression; parser_t parser;
symbol_table.add_vector("v0", v0); symbol_table.add_vector("v1", v1);
expression.register_symbol_table(symbol_table);
parser.register_vector_access_runtime_check(vec_rtc);
if (!parser.compile(expression_str, expression)) { printf("Error: %s\tExpression: %s\n", parser.error().c_str(), expression_str.c_str());
return;}
try { expression.value(); } catch(std::runtime_error& exception) { printf("Exception: %s\n",exception.what()); } }
Simple Example 21 - Cox, Ross and Rubinstein Binomial Option Pricing Model
The following example computes the prices of European Call and Put options for a given strike price using theCox-Ross-Rubinstein binomial option pricing model, and confirms the prices are somewhat arbitrage free by computing thePut-Call parity. The example demonstrates the use of vector processing, switch statements, user defined and expression local variables, numerical constants, conditional statements, for-loop structures, string comparisons and arithmetic functionality. [source: simple_example_21.cpp]
template void binomial_option_pricing_model() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string european_option_binomial_model_program = " var dt := t / n; " " var z := exp(r * dt); " " var z_inv := 1 / z; " " var u := exp(v * sqrt(dt)); " " var u_inv := 1 / u; " " var p_up := (z - u_inv) / (u - u_inv); " " var p_down := 1 - p_up; " " " " var option_price[n + 1] := [0]; " " " " for (var i := 0; i <= n; i += 1) " " { " " var base_price := s * u^(n - 2i); " " " " option_price[i] := " " switch " " { " " case callput_flag == 'call' : max(base_price - k, 0); " " case callput_flag == 'put' : max(k - base_price, 0); " " }; " " }; " " " " for (var j := n - 1; j >= 0; j -= 1) " " { " " for (var i := 0; i <= j; i += 1) " " { " " option_price[i] := z_inv * " " (p_up * option_price[i] + p_down * option_price[i + 1]); " " } " " }; " " " " option_price[0]; ";
T s = T( 100.00); // Spot / Stock / Underlying / Base price T k = T( 110.00); // Strike price T v = T( 0.30); // Volatility T t = T( 2.22); // Years to maturity T r = T( 0.05); // Risk free rate T n = T(1000.00); // Number of time steps
std::string callput_flag;
symbol_table_t symbol_table; symbol_table.add_variable("s",s); symbol_table.add_variable("k",k); symbol_table.add_variable("t",t); symbol_table.add_variable("r",r); symbol_table.add_variable("v",v); symbol_table.add_constant("n",n); symbol_table.add_stringvar("callput_flag",callput_flag);
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(european_option_binomial_model_program,expression);
callput_flag = "call";
const T binomial_call_option_price = expression.value();
callput_flag = "put";
const T binomial_put_option_price = expression.value();
printf("BinomialPrice(call, %5.3f, %5.3f, %5.3f, %5.3f, %5.3f) = %10.6f\n", s, k, t, r, v, binomial_call_option_price);
printf("BinomialPrice(put , %5.3f, %5.3f, %5.3f, %5.3f, %5.3f) = %10.6f\n", s, k, t, r, v, binomial_put_option_price);
const T put_call_parity_diff = (binomial_call_option_price - binomial_put_option_price) - (s - k * std::exp(-r * t));
printf("Put-Call parity difference: %20.17f\n", put_call_parity_diff); }
Simple Example 22 - Implied Volatility Of A European Option
The following example calculates the implied volatility of European Call and Put options for the same strike based on a given target price using the Newton-Raphson method, where the derivative of the option price with respect to its volatility will be itsVega. The example demonstrates the use of compositor functions, switch statements, conditional statements, user defined and expression local variables and constant variables, numerical constants, string comparisons, loop control structures, the ternary operator, inline statements, immutable symbol tables and arithmetic functionality. [source: simple_example_22.cpp]
template void compute_european_option_implied_volatility() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t; typedef exprtk::function_compositor compositor_t; typedef typename compositor_t::function function_t;
const std::string option_implied_volatility_program = " const var epsilon := 0.0000001; " " const var max_iters := 1000; " " " " var v := 0.5; /* Initial volatility guess */ " " var itr := 0; " " " " while ((itr += 1) <= max_iters) " " { " " var price := " " switch " " { " " case callput_flag == 'call' : bsm_call(s, k, r, t, v); " " case callput_flag == 'put' : bsm_put (s, k, r, t, v); " " }; " " " " var price_diff := price - target_price; " " " " if (abs(price_diff) <= epsilon) " " { " " break; " " }; " " " " var vega := bsm_vega(s, k, r, t, v); " " " " if (vega < epsilon) " " { " " itr := max_iters + 1; " " break; " " }; " " " " v -= price_diff / vega; " " }; " " " " itr <= max_iters ? v : null; ";
T s = T(100.00); // Spot / Stock / Underlying / Base price T k = T(110.00); // Strike price T t = T( 2.22); // Years to maturity T r = T( 0.05); // Risk free rate T target_price = T( 0.00);
std::string callput_flag;
symbol_table_t symbol_table(symbol_table_t::e_immutable); symbol_table.add_variable("s",s); symbol_table.add_variable("k",k); symbol_table.add_variable("t",t); symbol_table.add_variable("r",r); symbol_table.add_stringvar("callput_flag",callput_flag); symbol_table.add_variable ("target_price",target_price); symbol_table.add_pi();
compositor_t compositor(symbol_table);
compositor.add( function_t("bsm_call") .vars("s", "k", "r", "t", "v") .expression ( " var d1 := (log(s / k) + (r + v^2 / 2) * t) / (v * sqrt(t)); " " var d2 := d1 - v * sqrt(t); " " s * ncdf(d1) - k * exp(-r * t) * ncdf(d2); " ));
compositor.add( function_t("bsm_put") .vars("s", "k", "r", "t", "v") .expression ( " var d1 := (log(s / k) + (r + v^2 / 2) * t) / (v * sqrt(t)); " " var d2 := d1 - v * sqrt(t); " " k * exp(-r * t) * ncdf(-d2) - s * ncdf(-d1); " ));
compositor.add( function_t("bsm_vega") .vars("s", "k", "r", "t", "v") .expression ( " var d1 := (log(s / k) + (r + v^2 / 2) * t) / (v * sqrt(t)); " " s * exp(-d1^2 / 2) / sqrt(2pi) * sqrt(t); " ));
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(option_implied_volatility_program, expression);
{ callput_flag = "call"; target_price = T(18.339502);
const T call_option_implied_vol = expression.value();
printf("Call Option(s: %5.3f, k: %5.3f, t: %5.3f, r: %5.3f) "
"@ $%8.6f Implied volatility = %10.8f\n",
s, k, t, r, target_price, call_option_implied_vol);}
{ callput_flag = "put"; target_price = T(16.782764);
const T put_option_implied_vol = expression.value();
printf("Put Option(s: %5.3f, k: %5.3f, t: %5.3f, r: %5.3f) "
"@ $%8.6f Implied volatility = %10.8f\n",
s, k, t, r, target_price, put_option_implied_vol);} }
Simple Example 23 - 1D Real Discrete Fourier Transform
The following example will generate a specific waveform into the input vector, then proceed to compute its Discrete Fourier Transform placing it into the output vector. After which only significant frequency bins (aka phasors) and their associated power amplitudes will be written to stdout. The example demonstrates the use of compositor functions and symbol table embedding, user defined and expression local variables, numerical constants, vector processing, loop control structures, RTL IO and arithmetic functionality. [source: simple_example_23.cpp]
template void real_1d_discrete_fourier_transform() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t; typedef exprtk::function_compositor compositor_t; typedef typename compositor_t::function function_t;
const T sampling_rate = 1024.0; // ~1KHz const T N = 8 * sampling_rate; // 8 seconds worth of samples
std::vector input (static_caststd::size_t(N),0.0); std::vector output(static_caststd::size_t(N),0.0);
exprtk::rtl::io::println println;
symbol_table_t symbol_table; symbol_table.add_vector ("input" , input ); symbol_table.add_vector ("output" , output ); symbol_table.add_function ("println" , println ); symbol_table.add_constant ("N" , N ); symbol_table.add_constant ("sampling_rate", sampling_rate); symbol_table.add_pi();
compositor_t compositor(symbol_table); compositor.load_vectors(true);
compositor.add( function_t("dft_1d_real") .var("N") .expression ( " for (var k := 0; k < N; k += 1) " " { " " var k_real := 0.0; " " var k_imag := 0.0; " " " " for (var i := 0; i < N; i += 1) " " { " " var theta := 2pi * k * i / N; " " k_real += input[i] * cos(theta); " " k_imag -= input[i] * sin(theta); " " }; " " " " output[k] := hypot(k_real,k_imag); " " } " ));
const std::string dft_program = " " " /* " " Generate an aggregate waveform comprised of three " " sine waves of varying frequencies and amplitudes. " " / " " const var num_waves := 3; " " " " var frequencies[num_waves] := { 111.125, 222.250, 333.375 }; / Hz / " " var amplitudes [num_waves] := { 11.111, 22.222, 33.333 }; / Power */ " " " " for (var i := 0; i < N; i += 1) " " { " " var time := i / sampling_rate; " " " " for (var j := 0; j < frequencies[]; j += 1) " " { " " var frequency := frequencies[j]; " " var amplitude := amplitudes [j]; " " var theta := 2 * pi * frequency * time; " " " " input[i] += amplitude * sin(theta); " " } " " }; " " " " dft_1d_real(input[]); " " " " var freq_bin_size := sampling_rate / N; " " var max_bin := ceil(N / 2); " " var max_noise_level := 1e-6; " " " " /* Normalise amplitudes */ " " output /= max_bin; " " " " println('1D Real DFT Frequencies'); " " " " for (var k := 0; k < max_bin; k += 1) " " { " " if (output[k] > max_noise_level) " " { " " var freq_begin := k * freq_bin_size; " " var freq_end := freq_begin + freq_bin_size; " " " " println('Index: ', k,' ', " " 'Freq. range: [', freq_begin, 'Hz, ', freq_end, 'Hz) ', " " 'Amplitude: ', output[k]); " " } " " } " " ";
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(dft_program,expression);
expression.value(); }
Simple Example 24 - Reverse Polish Notation Expression Evaluator
The following example will evaluate single digit number based Reverse Polish Notation expressions. The example demonstrates the use of igeneric_function, string ranges, loop control structures, user defined and expression local variables, switch statements and general arithmetic functionality. [source: simple_example_24.cpp]
template <typename T, T Process(const unsigned char)> struct char_process : public exprtk::igeneric_function { typedef typename exprtk::igeneric_function igfun_t; typedef typename igfun_t::parameter_list_t parameter_list_t; typedef typename igfun_t::generic_type generic_type; typedef typename generic_type::string_view string_t;
using exprtk::igeneric_function::operator();
char_process() : exprtk::igeneric_function("S") {}
inline T operator()(parameter_list_t parameters) { const unsigned char c = string_t(parameters[0])[0]; return Process(c); } };
template T is_digit_func(const unsigned char c) { return (('0' <= c) && (c <= '9')) ? T(1) : T(0); }
template T to_num_func(const unsigned char c) { return static_cast(c - '0'); }
template void rpn_example() { typedef exprtk::symbol_table symbol_table_t; typedef exprtk::expression expression_t; typedef exprtk::parser parser_t;
const std::string rpn_program = " var stack[1000] := [0]; " " var top_index := 0; " " " " for (var i := 0; i < rpn_expression[]; i += 1) " " { " " var c := rpn_expression[i : i + 1]; " " " " if (c == ' ') " " { " " continue; " " } " " else if (is_digit(c)) " " { " " stack[top_index] := to_num(c); " " top_index += 1; " " } " " else " " { " " var operator := c; " " var operand1 := stack[top_index - 2]; " " var operand2 := stack[top_index - 1]; " " top_index -= 2; " " " " switch " " { " " case operator == '+' : stack[top_index] := operand1 + operand2; " " case operator == '-' : stack[top_index] := operand1 - operand2; " " case operator == '*' : stack[top_index] := operand1 * operand2; " " case operator == '/' : stack[top_index] := operand1 / operand2; " " case operator == '^' : stack[top_index] := operand1 ^ operand2; " " }; " " " " top_index += 1; " " } " " }; " " " " println(stack[0], ' = ', rpn_expression); " " ";
std::string rpn_expression;
char_process<T,is_digit_func > isdigit; char_process<T,to_num_func > tonum; exprtk::rtl::io::println println;
symbol_table_t symbol_table; symbol_table.add_stringvar("rpn_expression", rpn_expression); symbol_table.add_function ("println" , println ); symbol_table.add_function ("is_digit" , isdigit ); symbol_table.add_function ("to_num" , tonum );
expression_t expression; expression.register_symbol_table(symbol_table);
parser_t parser; parser.compile(rpn_program, expression);
const std::string rpn_expressions[] = { "2 3 8 / ^ 4 6 * + 3 9 / -", // 2 ^ (3 / 8) + 4 * 6 - 3 / 9 "1 2 / 6 5 2 - / * 7 +" , // (1 / 2) * (6 / (5 - 2)) + 7 "1 2 * 3 / 4 * 5 / 6 *" , // ((((1 * 2) / 3) * 4) / 5) * 6 "8 6 4 + * 2 /" // (8 * (6 + 4)) / 2 };
for (std::size_t i = 0; i < sizeof(rpn_expressions) / sizeof(std::string); ++i) { rpn_expression = rpn_expressions[i]; expression.value(); } }
Various Extended Examples
The proceeding examples demonstrate ExprTk's more advanced capabilities through practical yet simple to understand use cases:
- REPL Interface
- Simple Calculator Example
- Fizz-Buzz
- Collatz Conjecture
- Greatest Common Divisor
- Mandelbrot Fractal Generator (screenshot)
- Summation of Prime Factors
- Sieve of Eratosthenes
- Sieve of Eratosthenes (vectorized)
- Primes Via The Naive Method
- Miller-Rabin Probabilistic Primality Test
- Truth Table Generator
- Conway's Game of Life (animation)
- Sudoku Solver
- N-Queens Problem
- Magic Square Problem
- Tower Of Hanoi Example
- Maze Generator (maze.txt)
- Logical Deduction Riddle
- Recursive Fibonacci Example
- GNUPlot Curve Plotting Example
- GNUPlot Multi-Curve Plotting Example
- Basic Arithmetic Expression Parser And Evaluator
- Custom Real Type Adaptor
- Custom Complex Type Adaptor
- Custom Function Call Benchmark
- L-Norm of a Vector
- Nth-Root via the Bisection Method
- Vector Processing Benchmark
- Multi-Threaded Vector Processing Benchmark
- Maximum Subarray Sum (Kadane's Algorithm)
- Approximation of E via the Monte-Carlo Method
- Approximation of Pi via the Monte-Carlo Method
- Approximation of Pi via a Wiener Process Based Monte Carlo
- Approximation of Pi via Archimedes Method
- Ten Thousand Digits of Pi via Spigot Algorithm (pi_10kdigits.txt)
- Ten Thousand Digits of E via Spigot Algorithm (e_10kdigits.txt)
- Binomial Coefficient (n-choose-k) Example
- Pascal's Triangle (pascals_triangle.txt)
- Pythagorean Triples
- Pyramid Example (pyramid.txt)
- Fermat's Integer Factorization Method
- Pollard's Rho Integer Factorization Method
- Immutable Symbol Table Example
- CPU Instruction Primer
- Vector Processing Runtime Check Overhead Analysis
- Loop Timeout Runtime Check
- Compilation Timeout Check
- American Option Binomial Pricing Model
- Vectorized Binomial Model Based European Option Pricing
- Merton Jump Diffusion Process Based Option Pricing Model
- Monte-Carlo Based European Option Pricing Model
- Ornstein-Uhlenbeck Process
- Normal Random Variables Via Marsaglia Method
- Extract Expression Dependents
- Extract Symbol Table Functions
- Import Packages Example
- String Group Operations (add, create, contains, size, get, erase)
- Vector Resize Example
- Vector Resize Inline Within Expression Example
- Redefine Trignonmetry Functions In Terms Of Degrees Example
Supplementary Materials
- Investigation of a Performance Issue
- Extensive Math Parser Benchmark
- Library Documentation
- Source Documentation
- Functional Test Suite and Extended Functional Test Suite
- ExprTk Symbol Regex and Validation
- Code Coverage Report
- Stackoverflow Questions
- Citing ExprTk
- Why Use ExprTk
Benchmarks
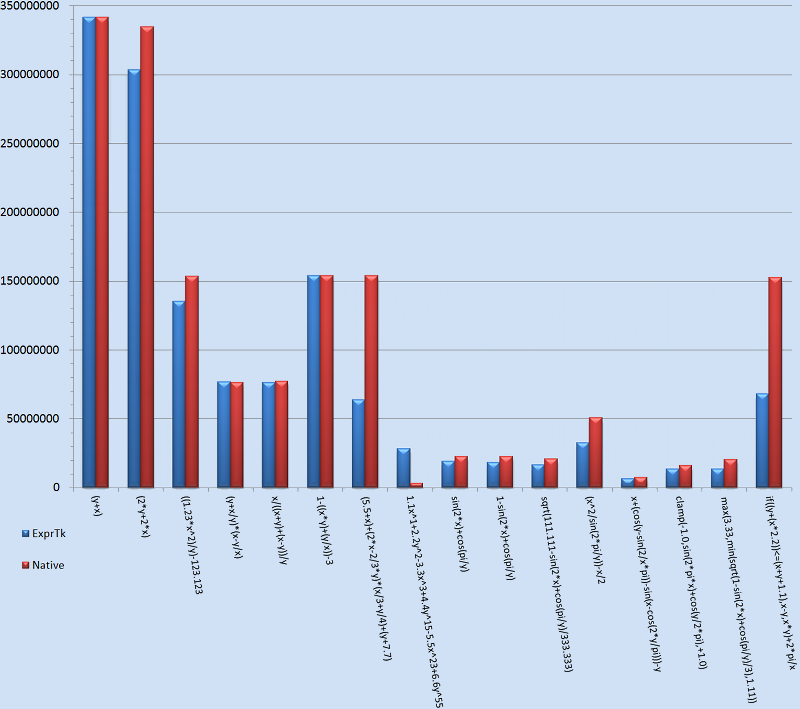
The chart below depicts the rate of expression evaluations per second for an assortment of expressions. Each expression is specialised upon the 'double' floating point type and comprised of two variables that are varied before each expression evaluation. The expressions are evaluated in two modes: ExprTk compiled and native optimised. The benchmark itself was compiled using GCC 7.2 with O3, LTO, PGO and native architecture target compiler settings, and executed upon an Intel Xeon E5-2687W 3GHz CPU, 64GB RAM, Ubuntu 17.10 with kernel 4.10 system.Source: exprtk_benchmark.cpp
(y + x)(2 * y + 2 * x)((1.23 * x^2) / y) - 123.123(y + x / y) * (x - y / x)x / ((x + y) + (x - y)) / y1 - ((x * y) + (y / x)) - 31.1x^1 + 2.2y^2 - 3.3x^3 + 4.4y^15 - 5.5x^23 + 6.6y^55sin(2 * x) + cos(pi / y)1 - sin(2 * x) + cos(pi / y)sqrt(111.111 - sin(2 * x) + cos(pi / y) / 333.333)(x^2 / sin(2 * pi / y)) -x / 2x + (cos(y - sin(2 / x * pi)) - sin(x - cos(2 * y / pi))) - yclamp(-1.0, sin(2 * pi * x) + cos(y / 2 * pi), +1.0)max(3.33, min(sqrt(1 - sin(2 * x) + cos(pi / y) / 3), 1.11))if (avg(x,y) <= x + y, x - y, x * y) + 2 * pi / x
Renaissance Technologies - Rentec https://www.rentec.com
TGS Management Company - TGS https://www.tgsmc.com
Black-Scholes-Merton Option Pricing Model Benchmark
The following is a benchmark based on Example 15. The BSM option pricing model is executed using native and ExprTk based implementations. There are two ExprTk implementations, vanilla and another where e(...) is replaced with the equivalent and much faster exp(...) function and also repeated sub-calculations are cached locally. The benchmark depicts the number of pricing calculations per second. The benchmark itself was compiled using GCC 7.2 with O3, LTO, PGO and native architecture target compiler settings, and executed upon an Intel Xeon E5-2687W 3GHz CPU, 64GB RAM, Ubuntu 17.10 with kernel 4.10 system.Source: exprtk_bsm_benchmark.cpp

ExprTk Notes
The following is a list of facts and suggestions one may want to take into account when using ExprTk:
- Note 00: Precision and performance of expression evaluations are the dominant principles of the ExprTk library.
- Note 01: ExprTk uses a rudimentary imperative programming model with syntax based on languages such as Pascal and C. Furthermore ExprTk is an LL(2) type grammar and is processed using a recursive descent parsing algorithm.
- Note 02: Supported types are float, double, long double and MPFR/GMP. Generally any user defined numerical type that supports all the basic floating point arithmetic operations: -, +, *, /, ^, % etc; unary and binary operations: sin, cos, min, max, equal etc and any other ExprTk dependent operations can be used to specialise the various components: expression, parser and symbol_table.
- Note 03: Standard arithmetic operator precedence is applied (BEDMAS). In general C, Pascal or Rust equivalent unary, binary, logical and equality/inequality operator precedence rules apply. eg:
a == b and c > d + 1 ---> (a == b) and (c > (d + 1)) x - y <= z / 2 ---> (x - y) <= (z / 2) a - b / c * d^2^3 ---> a - ((b / c) * d^(2^3)) - Note 04: Results of expressions that are deemed as being 'valid' are to exist within the set of Real numbers. All other results will be of the value: Not-A-Number (NaN). However this may not necessarily be a requirement for user defined numerical types, eg: complex number type.
- Note 05: Supported user defined types are numeric and string variables, numeric vectors and functions.
- Note 06: All reserved words, keywords, variable, vector, string and function names are case-insensitive.
- Note 07: Variable, vector, string variable and function names must begin with a letter (A-Z or a-z), then can be comprised of any combination of letters, digits, underscores and non-consecutive dots, ending in either a letter (A-Z or a-z), digit or underscore. (eg: x, y2, var1, power_func99, person.age, item.size.0). The associated regex pattern is:
[a-zA-Z][a-zA-Z0-9_]*(\.[a-zA-Z0-9_]+)* - Note 08: Expression lengths and sub-expression lists are limited only by storage capacity.
- Note 09: The life-time of objects registered with or created from a specific symbol-table must span at least the lifetime of the symbol table instance and all compiled expressions which utilise objects, such as variables, strings, vectors, function compositor functions and functions of that symbol-table, otherwise the result will be undefined behaviour.
- Note 10: Equal and not_equal are normalised-epsilon equality routines, which use epsilons of 0.0000000001 and 0.000001 for double and float types respectively.
- Note 11: All trigonometric functions assume radian input unless stated otherwise.
- Note 12: Expressions may contain white-space characters such as space, tabs, new-lines, control-feed et al.('\n', '\r', '\t', '\b', '\v', '\f')
- Note 13: Strings may be comprised of any combination of letters, digits special characters including (~!@#$%^&*()[]|=+ ,./?<>;:"`~_) or hexadecimal escaped sequences (eg: \0x30) and must be enclosed with single-quotes.
eg: 'Frankly my dear, \0x49 do n0t give a damn!' - Note 14: User defined normal functions can have up to 20 parameters, where as user defined generic-functions and vararg-functions can have an unlimited number of parameters.
- Note 15: The inbuilt polynomial functions can be at most of degree 12.
- Note 16: Where appropriate constant folding optimisations may be applied. (eg: The expression '2 + (3 - (x / y))' becomes '5 - (x / y)')
- Note 17: If the strength reduction compilation option has been enabled, then where applicable strength reduction optimisations may be applied.
- Note 18: String processing capabilities are available by default. To turn them off, the following needs to be defined at compile time: exprtk_disable_string_capabilities
- Note 19: Composited functions can call themselves or any other functions that have been defined prior to their own definition.
- Note 20: Recursive calls made from within composited functions will have a stack size bound by the stack of the executing architecture.
- Note 21: User defined functions by default are assumed to have side effects. As such an "all constant parameter" invocation of such functions wont result in constant folding. If the function has no side-effects then that can be noted during the constructor of the ifunction allowing it to be constant folded where appropriate.
- Note 22: The entity relationship between symbol_table and an expression is many-to-many. However the intended 'typical' use-case where possible, is to have a single symbol table manage the variable and function requirements of multiple expressions.
- Note 23: The common use-case for an expression is to have it compiled only ONCE and then subsequently have it evaluated multiple times. An extremely inefficient and suboptimal approach would be to recompile an expression from its string form every time it requires evaluating.
- Note 24: It is strongly recommended that the return value of method invocations from the parser and symbol_table types be taken into account. Specifically the 'compile' method of the parser and the 'add_xxx' set of methods of the symbol_table as they denote either the success or failure state of the invoked call. Continued processing from a failed state without having first rectified the underlying issue will in turn result in further failures and undefined behaviours.
- Note 25: The following are examples of compliant floating point value representations:
12345-123.456+123.456e+12123.456E-12+012.045e+07.12341234.-56789.123.456f-321.654E+3L
- Note 26: Expressions may contain any of the following comment styles:
// .... \n# .... \n/* .... */
- Note 27: The 'null' value type is a special non-zero type that incorporates specific semantics when undergoing operations with the standard numeric type. The following is a list of type and boolean results associated with the use of 'null':
null +,-,*,/,% x --> xx +,-,*,/,% null --> xnull +,-,*,/,% null --> nullnull == null --> truenull == x --> truex == null --> truex != null --> falsenull != null --> falsenull != x --> false
- Note 28: The following is a list of reserved words and symbols used by ExprTk. Attempting to add a variable or custom function to a symbol table using any of the reserved words will result in a failure.
abs, acos, acosh, and, asin, asinh, assert, atan, atanh, atan2, avg, break, case, ceil, clamp, continue, const, cos, cosh, cot, csc, default, deg2grad, deg2rad, equal, erf, erfc, exp, expm1, false, floor, for, frac, grad2deg, hypot, iclamp, if, else, ilike, in, inrange, like, log, log10, log2, logn, log1p, mand, max, min, mod, mor, mul, ncdf, nand, nor, not, not_equal, null, or, pow, rad2deg, repeat, return, root, round, roundn, sec, sgn, shl, shr, sin, sinc, sinh, sqrt, sum, swap, switch, tan, tanh, true, trunc, until, var, while, xnor, xor - Note 29: Every valid ExprTk statement is a "value returning" expression. Unlike some languages that limit the types of expressions that can be performed in certain situations, in ExprTk any valid expression can be used in any "value consuming" context. eg:
var y := 3;
for (var x := switch
{
case 1 : 7;
case 2 : -1 + ~{var x{};};
default : y > 2 ? 3 : 4;
};
x != while (y > 0) { y -= 1; };
x -= {
if (min(x,y) < 2 * max(x,y))
x + 2;
else
x + y - 3;
}
)
{
(x + y) / (x - y);
}; - Note 30: It is recommended when prototyping expressions that theExprTk REPL be utilised, as it supports all the features available in the library, including complete error analysis, benchmarking and dependency dumps etc which allows for rapid coding/prototyping and debug cycles without the hassle of having to recompile test programs with expressions that have been hard-coded. It is also a good source of truth for how the library's various features can be applied.
- Note 31: For performance considerations, one should assume the actions of expression, symbol table and parser instance instantiation and destruction, and the expression compilation process itself to be of high latency. Hence none of them should be part of any performance critical code paths, and should instead occur entirely either before or after such code paths.
- Note 32: Deep copying an expression instance for the purposes of persisting to disk or otherwise transmitting elsewhere with the intent to 'resurrect' the expression instance later on is not possible due to the reasons described in the final note of Section 10. The recommendation is to instead simply persist the string form of the expression and compile the expression at run-time on the target.
- Note 33: The correctness and robustness of the ExprTk library is maintained by having a comprehensive suite of unit tests and functional tests all of which are run using sanitizers (ASAN, UBSAN, LSAN, MSAN, TSAN). Additionally, continuous fuzz-testing provided by Google OSS Fuzz, and static analysis viaSynopsys Coverity.
Note 34: The library name ExprTk is pronounced "Ex-Pee-Ar-Tee-Kay" or simply**"Mathematical Expression Toolkit"**.
- Note 35: Before jumping in and using ExprTk, do take the time to peruse the documentation and all of the examples, both in the main and the extras distributions. Having an informed general view of what can and can't be done, and how something should be done with ExprTk, will likely result in a far more productive and enjoyable programming experience.
ExprTk Users
The following is a brief listing of some of the users of the ExprTk library:
 |
 |
 |
 |
|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|
Support and Consulting Services
 |
Consulting services for ExprTk are available, these include: Project integration Additional features and customisations Custom language/DSL implementations Performance enhancements For more information or to raise an issue or bug report please reach out via the contact page. |
|---|