pymc.NegativeBinomial — PyMC 5.23.0 documentation (original) (raw)

class pymc.NegativeBinomial(name, *args, **kwargs)[source]#

Negative binomial distribution.

The negative binomial distribution describes a Poisson random variable whose rate parameter is gamma distributed. Its pmf, parametrized by the parameters alpha and mu of the gamma distribution, is

\[f(x \mid \mu, \alpha) = \binom{x + \alpha - 1}{x} (\alpha/(\mu+\alpha))^\alpha (\mu/(\mu+\alpha))^x\]

(Source code, png, hires.png, pdf)

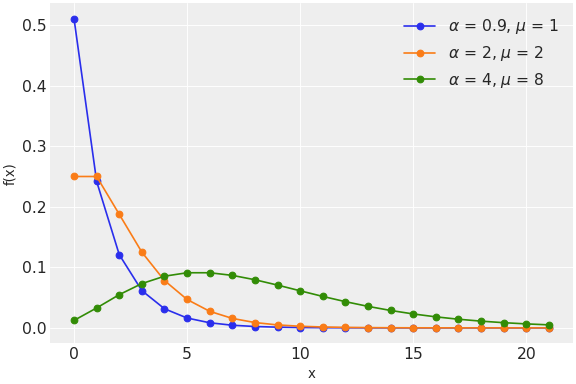
The negative binomial distribution can be parametrized either in terms of mu or p, and either in terms of alpha or n. The link between the parametrizations is given by

\[\begin{split}p &= \frac{\alpha}{\mu + \alpha} \\ n &= \alpha\end{split}\]

If it is parametrized in terms of n and p, the negative binomial describes the probability to have x failures before the n-th success, given the probability p of success in each trial. Its pmf is

\[f(x \mid n, p) = \binom{x + n - 1}{x} (p)^n (1 - p)^x\]

Parameters:

alphatensor_like of float

Gamma distribution shape parameter (alpha > 0).

mutensor_like of float

Gamma distribution mean (mu > 0).

ptensor_like of float

Alternative probability of success in each trial (0 < p < 1).

ntensor_like of float

Alternative number of target success trials (n > 0)

Methods