「Random Walk」の意味や使い方 わかりやすく解説 Weblio辞書 (original) (raw)
概要
によって定義されるマルコフ連鎖. すべての  に対して
に対して 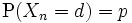 ,
, 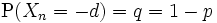 であるときを単純ランダムウォークといい, さらに
であるときを単純ランダムウォークといい, さらに 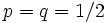 のとき, 単純ランダムウォークは対称であるという. 壁によって動きを遮られたり, 動く範囲が制限されるランダムウォークを考えることもできる.
のとき, 単純ランダムウォークは対称であるという. 壁によって動きを遮られたり, 動く範囲が制限されるランダムウォークを考えることもできる.
詳説
ランダム・ウォーク (random walk) とその連続化であるブラウン運動は, でたらめな動きを表現する最も基本的な確率過程で, 幅広い応用がある.
ランダム・ウォーク 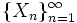 を互いに独立で同一の分布に従う確率変数の列とするとき,
を互いに独立で同一の分布に従う確率変数の列とするとき,
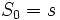 (定数),
(定数), 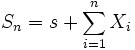
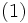
によって定義される確率過程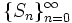 をランダム・ウォークと呼ぶ. 特に, ある
をランダム・ウォークと呼ぶ. 特に, ある 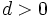 およびすべての
およびすべての  に対して,
に対して, 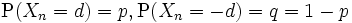 であるとき,
であるとき, 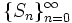 は (1次元の) 単純ランダム・ウォークであるといい, さらに
は (1次元の) 単純ランダム・ウォークであるといい, さらに 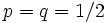 のとき, 単純ランダム・ウォークは対称であるという. また, 「壁」によって動きが止められたり, 動く範囲が制限されるランダム・ウォークを考えることもできる.
のとき, 単純ランダム・ウォークは対称であるという. また, 「壁」によって動きが止められたり, 動く範囲が制限されるランダム・ウォークを考えることもできる. 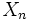 の独立性より, ランダム・ウォークはマルコフ過程となる.
の独立性より, ランダム・ウォークはマルコフ過程となる.
初期値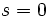 のランダム・ウォークにおいて,
のランダム・ウォークにおいて,  ステップ後の位置の期待値と分散は, それぞれ
ステップ後の位置の期待値と分散は, それぞれ 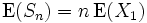 ,
, 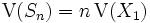 となり, 時間の経過に比例する. 分散が時間の経過に比例することから, ランダム・ウォークは時間が経つにつれて次第に拡散していくことが分かる.
となり, 時間の経過に比例する. 分散が時間の経過に比例することから, ランダム・ウォークは時間が経つにつれて次第に拡散していくことが分かる.
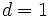 ,
, 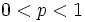 として得られる単純ランダム・ウォーク
として得られる単純ランダム・ウォーク 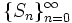 は, 整数を状態空間とする周期2の既約なマルコフ連鎖である. このマルコフ連鎖は
は, 整数を状態空間とする周期2の既約なマルコフ連鎖である. このマルコフ連鎖は 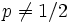 のとき一時的であり,
のとき一時的であり, 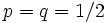 ならば零再帰的となる. たとえば
ならば零再帰的となる. たとえば 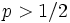 ならば
ならば 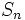 はだんだん大きくなっていく傾向があり, 正の方へドリフトする. このため出発点に戻ることは保証できなくなり一時的となるのである.
はだんだん大きくなっていく傾向があり, 正の方へドリフトする. このため出発点に戻ることは保証できなくなり一時的となるのである.
2次元の対称な単純ランダム・ウォーク(2次元格子点空間上の4つの隣接点にそれぞれ確率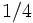 で推移する) は零再帰的, 3次元以上の単純ランダム・ウォークはすべて一時的であることも知られている [1].
で推移する) は零再帰的, 3次元以上の単純ランダム・ウォークはすべて一時的であることも知られている [1].
単純ランダム・ウォークからブラウン運動へ 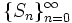 を初期値
を初期値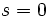 の対称な単純ランダム・ウォークとする. このランダム・ウォークが1ステップ進むのに
の対称な単純ランダム・ウォークとする. このランダム・ウォークが1ステップ進むのに 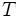 だけ時間がかかるとして,
だけ時間がかかるとして, 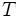 と
と 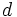 を同時に0に近づけることを考える.
を同時に0に近づけることを考える. 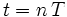 に対して, 時刻
に対して, 時刻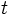 にランダム・ウォークが
にランダム・ウォークが 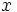 にいる確率を
にいる確率を 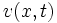 と表すと,
と表すと, 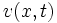 は差分方程式
は差分方程式 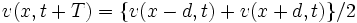 を満たすので,
を満たすので,
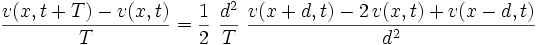
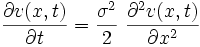
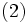
を得る. 式 (2) は拡散方程式 (diffusion equation) と呼ばれ, その解は初期条件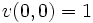 ,
, 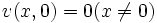 のもとで, 正規分布
のもとで, 正規分布 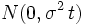 の密度関数となる. より一般的には, 初期値が0の (必ずしも対称でない) 単純ランダム・ウォークにおいて,
の密度関数となる. より一般的には, 初期値が0の (必ずしも対称でない) 単純ランダム・ウォークにおいて, 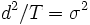 ,
, 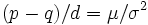 を保ったまま
を保ったまま 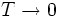 とすると, 時刻
とすると, 時刻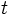 での位置が正規分布
での位置が正規分布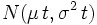 に従う確率過程が得られる [1].
に従う確率過程が得られる [1].
ブラウン運動 イギリスの植物学者ブラウン (R. Brown) は, 水面に浮く花粉中の微粒子が極めて不規則な動きをすることを見いだした. アインシュタイン (A. Einstein) は, この運動が拡散方程式 (2) によって特徴づけられることを示し, その後ウィナー (N. Wiener) らによって確率過程としての基盤が築かれた. この確率過程をブラウン運動 (Brownian motion) またはウィーナー過程 (Wiener process) と呼ぶ.
(1次元の) ブラウン運動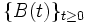 は次の性質を満たす実数値確率過程である:
は次の性質を満たす実数値確率過程である:
3. 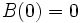 かつ
かつ 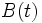 は
は 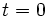 で連続.
で連続.
1. より, 時刻 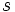 以降の
以降の 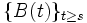 の振る舞いは
の振る舞いは 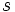 までの履歴には依存しないため, ブラウン運動はマルコフ過程である. さらに, ブラウン運動が強マルコフ性を持つこと, 標本路が連続となることも知られている [2].
までの履歴には依存しないため, ブラウン運動はマルコフ過程である. さらに, ブラウン運動が強マルコフ性を持つこと, 標本路が連続となることも知られている [2].
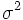 を拡散係数と呼び, 特に
を拡散係数と呼び, 特に 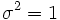 のブラウン運動を標準ブラウン運動と呼ぶ. また,
のブラウン運動を標準ブラウン運動と呼ぶ. また, 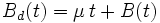 によって定まる
によって定まる 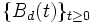 をドリフトを持つブラウン運動と呼び,
をドリフトを持つブラウン運動と呼び, 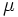 をドリフト係数と呼ぶ.
をドリフト係数と呼ぶ.
鏡像原理 ドリフトのないブラウン運動 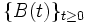 に対して
に対して 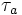 を
を 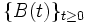 が初めて
が初めて 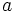 を横切る時刻とすると,
を横切る時刻とすると, 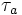 は停止時 (stopping time) となる.
は停止時 (stopping time) となる. 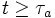 において
において 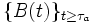 と
と 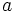 に関して対称な標本路を持つ確率過程
に関して対称な標本路を持つ確率過程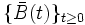 を
を
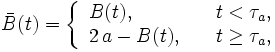
で定める. 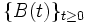 が強マルコフ性を持つことと,
が強マルコフ性を持つことと, 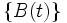 と
と 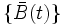 の対称性から,
の対称性から, 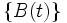 と
と 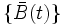 は同じ確率法則に従うことがわかる. 一般にこのような性質を鏡像原理 (reflection principle) と呼び, 初到達時間の分布などを求める際に利用される.
は同じ確率法則に従うことがわかる. 一般にこのような性質を鏡像原理 (reflection principle) と呼び, 初到達時間の分布などを求める際に利用される.
拡散過程 ドリフト係数や拡散係数が位置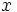 や時刻
や時刻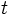 に依存した値
に依存した値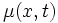 ,
, 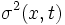 をとるように一般化して得られる確率過程
をとるように一般化して得られる確率過程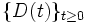 を拡散過程 (diffusion process) と呼び,
を拡散過程 (diffusion process) と呼び, 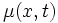 と
と 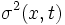 を, それぞれドリフト関数, 拡散関数と呼ぶ. 拡散過程は強マルコフ性を持ち, その標本路は連続である. 逆に, 連続な標本路を持つマルコフ過程は拡散過程となることが知られている.
を, それぞれドリフト関数, 拡散関数と呼ぶ. 拡散過程は強マルコフ性を持ち, その標本路は連続である. 逆に, 連続な標本路を持つマルコフ過程は拡散過程となることが知られている.
ブラウン運動や拡散過程の標本路は, 連続であるがいたるところで微分不可能という性質を持っている. このため拡散過程の解析においては, 確率積分や確率微分方程式といった通常の微分や積分とは異なる概念が必要となる [3, 4].
[1] W. Feller, An Introduction to Probability Theory and Its Applications, Volume 1, 2nd Ed., John Wiley & Sons, 1957. 河田龍夫監訳, 『確率論とその応用 I』, 紀伊国屋書店, 1960 (上巻), 1961 (下巻).
[2] K. Itô and H. P. McKean, Diffusion Processes and Their Sample Paths, Second Printing, Springer-Verlag, 1996.
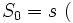
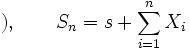
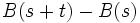 は
は