多目的計画とは何? わかりやすく解説 Weblio辞書 (original) (raw)
読み方:たもくてきけいかく
【英】:multiobjective programming
概要
従来の数理計画法がただ1つの目的関数の最小化を目指しているのに対し, 複数の目的関数の同時最小化を考える計画法. コストと性能といった直接に競合する目的を考える場合はもちろん, 複数時点での評価を考える場合や, 複数の可能性に対する評価を考える場合なども多目的となる. 複数の目的を同時に最小にする解は存在しないのが普通であるから, 目的関数間のトレードオフを考慮して, 意思決定者にとって最も好ましい解を選ぶことが目標となる.
詳説
我々が現実世界において遭遇する意思決定問題には, 複数の評価尺度(目的)があることが多い. このような問題を多基準意思決定問題あるいは多目的意思決定問題と呼ぶ. このような問題の数理計画法としての定式化とその解決方法を考えるのが多目的計画である.
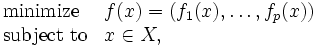
という形に定式化される. ここで  は実行可能集合であるが, 通常の1目的の数理計画問題と同様, 不等式制約や等式制約で表現されることが多い.
は実行可能集合であるが, 通常の1目的の数理計画問題と同様, 不等式制約や等式制約で表現されることが多い.
通常の数理計画問題(最適化問題)であれば, 実数の大小関係が全順序であることから, 最適解の概念は明瞭であるが, 多目的の場合は一方が良くとも他方が悪くなることが生じるため順序関係が半順序となり, 考察を要する. 基本となるのは, パレート最適解 (単にパレート解または非劣解, 有効解) と呼ばれる解である. 実行可能解 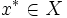 は別の実行可能解
は別の実行可能解 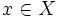 で
で
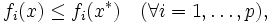
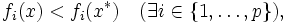
となるものが存在しないとき, パレート最適解であるといわれる. これを少し弱めた解として弱パレート最適解が, また強めた解として真性パレート最適解がある. さらに, 意思決定の観点からいえば, 最終的に意思決定者にとって最も好ましい解をパレート最適解の中から選ぶことが問題となるが, この解のことを意思決定者の選好解という.
通常の数理計画における理論的成果を, 多目的計画の場合に拡張する研究はこれまで多くなされてきている. まずパレート最適解を特徴づける最適性の条件は, キューン・タッカー条件を拡張した形で得られている. また多目的計画に対する双対性や安定性, 感度分析などの研究も進んでいる. ただし, 通常の問題であればその最適値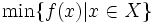 は一意に定まる(厳密には,
は一意に定まる(厳密には, 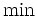 を
を 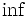 で置き換え,
で置き換え, 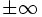 を許容する場合もある). これに対し多目的のパレート最適解は一意には定まらないのが普通であり, パレート最適値(パレート最適解に対応する目的関数値)全体が一つの集合を与える. したがって, 通常の最適値関数に対応するものとして, いわゆる最適値写像あるいは摂動写像と呼ばれる集合値写像(点対集合写像)を考える必要がある. これらの理論的結果については [1][3] に詳しい.
を許容する場合もある). これに対し多目的のパレート最適解は一意には定まらないのが普通であり, パレート最適値(パレート最適解に対応する目的関数値)全体が一つの集合を与える. したがって, 通常の最適値関数に対応するものとして, いわゆる最適値写像あるいは摂動写像と呼ばれる集合値写像(点対集合写像)を考える必要がある. これらの理論的結果については [1][3] に詳しい.
さて, 意思決定者の選好解を求めるには, 大きく分けて以下に述べる3つのアプローチがある.
- パレート最適解のすべて(もしくは十分多く)を求め, それを意思決定者に提示して, 選考解を決定してもらう.
- 意思決定者の選好を表す実数値関数である価値関数(もしくは効用関数)を求め, それを最適化する通常の数理計画問題を解く.
- コンピュータによるパレート最適解の導出とその解に基づく意思決定者の局所的な選好情報を用いて, 両者の対話を繰り返すことにより, 選好解を求める.
まず, 最初のアプローチは特に目的関数の数が少ない(例えば2目的の)場合や, 実行可能解が比較的少数の有限個しか存在しないような場合であれば, 有効となる. 実際にパレート最適解を求めるには, もとの多目的計画問題を何らかのパラメータを含む通常の数理計画問題に変換するスカラー化を行う. この方法として代表的なものは次の3つである.
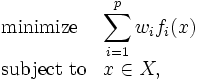
を解く. 簡明で分かり易いが, 非凸な問題の場合には欠陥がある.
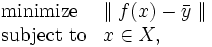
を解く. ノルムとしては, 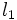 ノルム(目標計画はこの場合に相当する)やチェビシェフノルムなどが考えられる. また実際にはこれを拡張したチェビシェフスカラー化関数を用いたり, 目的関数に重みを導入したりする.
ノルム(目標計画はこの場合に相当する)やチェビシェフノルムなどが考えられる. また実際にはこれを拡張したチェビシェフスカラー化関数を用いたり, 目的関数に重みを導入したりする.
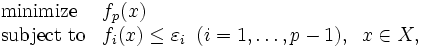
を解く.
次に2番目のアプローチの価値関数(効用関数)の同定については, 多属性効用理論がよく知られている. この際大切なことは, 目的関数間の独立性が十分確保されていることである. 詳細については [4] に詳しい. なお, 上に挙げた加重和目的関数やノルム関数を効用関数として想定し, そのパラメータを同定するのも, このアプローチの簡略版と考えられる.
最後のアプローチが対話型解法とよばれているもので, コンピュータによる候補解の算出と意思決定者による選好情報の提示を交互に繰り返していくことにより, 選好解を探索する. 両者の情報交換の仕方によって, いくつもの方法が考えられているが, 人間が関わっているだけに, ヒューマンフレンドリーな方法であることが望まれる. 現在までに提案された主な対話型解法については [2]に詳しい. 日本語では [3]に希求水準法を中心とした説明がある. さらには,まだ研究が進んでいないが, DEAを応用して, 選好解を選ぶ方法も考えられている.
[1] Y. Sawaragi, H. Nakayama and T. Tanino, Theory of Multiobjective Optimization, Academic Press, 1985.
[2] K. M. Miettinen, Nonlinear Multiobjective Optimization, Kluwer Academic, 1999.
 個の
個の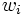 を
を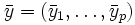 からの
からの