Tests and Measurements for the Parent, Teacher, Advocate and Attorney: How to Use Test Scores to Identify Needs and Measure Progress on IEP Goals- by Peter Wright and Pamela Wright (original) (raw)
Let's look at the performance of a group of children. You need to understand how an individual child scores when compared with other children who are his age or in his grade --- and what this means.
First, we'll examine a single component of physical fitness in a group of elementary school students. Our group or sample consists of 100 fifth grade students. These children are enrolled in a physical fitness class to prepare them to take the President's Physical Fitness Challenge. We will assume that the average chronological age (CA) of these children is exactly ten years, zero months. (CA=10-0) The children are tested in September, at the beginning of the school year.
To qualify as "physically fit," each child must meet several goals. Push-ups are one measure of upper body strength. Each child must complete as many push-ups as possible in a period of time. Each child's raw score is the number of push-ups completed. The term raw score is simply another way of describing the number of items correctly answered or performed.
After all fifth grade students complete the push-up test, their scores are listed. The results are as follows:
Again, two-thirds of the children in this fifth grade class were able to complete between 7 and 13 push-ups. The remaining third of the children did fewer than 7 or more than 13 push-ups. Nearly all of the children --- 98 out of 100 --- were able to complete between 4 and 16 push-ups. Click here to view the bell curve chart.
The test results provide us with a sample of data. As we analyze the data in our sample, we can compare the performance of any individual child with that of the entire group. As we make these comparisons, the data will enable us to recognize any child's strengths and weaknesses when compared with the peer group of similar youngsters.
If we conduct an identical push-up test with children in other grades, we can compare our original group of 100 fifth grade children with other groups of youngsters --- children who are older, younger, in different grades, in different schools. If we gather enough information or data from other sources, we can compare our original group of fifth graders --- or an individual child within our group --- to a national population of children who are being tested for their upper body strength as measured by their ability to do push-ups.
Using the Bell Curve to Measure Progress
In nature, traits and characteristics distribute themselves along theoretical curves. For our purposes, the most important curve is called the normal frequency distribution or bell curve. Because the percentages along the bell curve are well-known and thoroughly researched, they become our frame of reference.
By using the bell curve, we can develop a diagram or graph of the children's push-up scores. This map --- on the bell curve --- provides us with additional information. We can see what percentage of children were able to complete specific numbers of push-ups. When we use the bell curve, we can visually demonstrate where any particular child scores, when compared with other children who are the same age or in the same grade. Likewise, with educational test scores, we can visually demonstrate scores and change over time.
If we compare the push-up scores obtained by children who attend different schools, we can determine whether the physical fitness of children, as measured by their ability to do push-ups, varies in different schools, neighborhoods, states, or countries.
We can also measure progress over time --- with push-ups and with improvement in reading skills. Let's look at our class of fifth graders again. We want to gather information as to whether the physical fitness class is effective --- whether the children's fitness levels improve. How can we answer this question?
To measure the effectiveness of the fitness class, we will measure the children's number of push-ups before they take the class and compare this score with their score after they take the class. If the class is effective, we should see individual improvement and group improvement. Some children will have minimal improvement --- these children will fall further behind the peer group. Other children who performed below their peers may show significant improvement. Some children will improve so much that they now perform as well or better than the "average" youngster.
We will measure the children's progress on one or more occasions as they progress through the class. If the fitness class is "working," that is, if the children's' fitness levels are improving, their ability to perform fitness skills should improve measurably over time. In our example, physical fitness improvement is being measured with "technically sound instruments" that "are valid and reliable" (34 C.F.R. §300.404(b)(c)) and use "Data-based documentation of repeated assessments of achievement at reasonable intervals, reflecting formal assessment of student progress ..." (34 C.F.R. §300.309(b)(2))
Because of its value and usefulness in measuring educational progress, we will return to the subject of the bell curve repeatedly throughout this article.
The Bell Curve: Basic Concepts
On all bell curves, the bottom or horizontal line is called the X axis. In our sample of fifth graders, the X axis represents "number of push-ups." And, on all bell curves, the up- and- down vertical line is called the Y axis. In our sample, the Y axis represents the number of children who earned a specific score (number of push-ups completed).
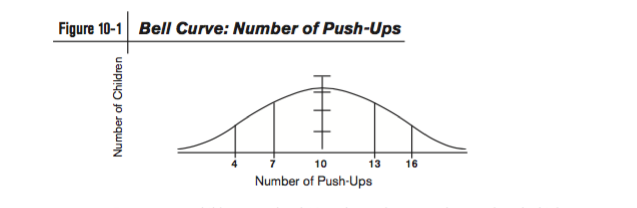
As you can see in the diagram above, the highest point of the bell curve on the X axis is equal to a score of 10 push-ups. You recall that more children completed 10 push-ups than any other number. Thus, the highest point on this bell curve represents a score of 10. The next most frequently obtained scores were 9 and 11, followed by 8 and 12. This pattern continues out toward the far ends of the bell curve. In our example, the ends occurred at 1 and 19 push-ups.
Using the bell curve, we can now chart each child's score and compare it to the score achieved by all 100 students in the class. Look at the bell curve above, and find 10 push-ups. We know that Amy completed 10 push-ups so her raw score was 10. Ten push-ups placed her squarely in the middle of the class. Half of the youngsters in Amy's class earned a score of 10 or more; half of the children scored 10 or less. If you look at the bell curve diagram (below), you see that Amy's score of 10 placed her at the 50% level. The individual's percent level is referred to as their percentile rank (PR). Amy's percentile rank is 50 (PR=50).
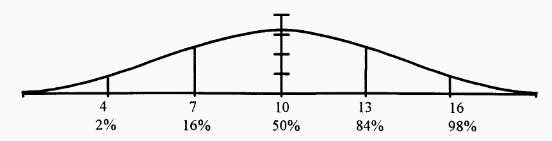
Erik completed 13 push-ups. Looking at the bell curve above, you see that his score of 13 placed him at the 84th percent level. Erik's percentile rank is 84 (PR=84). Erik's ability to do push-ups placed him in the 84th position out of the 100 fifth grade children tested on upper body strength.
Sam completed 7 push-ups. His raw score of 7 placed him at the (bottom) 16 percent. Sam's percentile rank was 16 (PR=16). Out of our sample of 100 fifth grade children, 84 children earned a higher score than Sam.
Larry completed 6 push-ups. We can convert his raw score of 6 to a percentile rank of 9 (PR=9). 91 children scored higher and 8 children scored lower than Larry in upper body strength as measured by the ability to do push-ups.
Oscar completed 2 push-ups. His raw score of 2 placed him in the bottom 1 percent of fifth graders tested (PR=1).
Nancy's raw score of 17 placed her at the upper 99 percent. We say that Nancy scored at the 99th percentile rank (PR=99).
You can see the relationship between the number of push-ups completed and the child's percentile rank (PR) reproduced in the table below: Click here to see the table
The bell curve is a powerful tool. When you use the bell curve, you can objectively compare any child's percentile rank to that of a group of children. You can also compare a single child's progress or regression when compared to the group.
Using the bell curve, you can compare a single child's score to the scores obtained by other children who are older or younger or in different grades.
Let's see how this works. Again, we will measure the children's upper body strength by the number of push-ups they can perform. In this case, we decide to evaluate all children in all the elementary grades, from Kindergarten through fifth grade. We will assume that the average chronological age of these elementary school children is exactly eight years (CA=8-0 years).
After we test the third graders, we find that the average or mean score of our sample of 100 eight year old third graders is 6 push-ups. This means that the "average" third grade child (who is 8 years old) can do 6 push-ups. We can also compare an individual child's score on arithmetic problems answered correctly with the average number answered correctly by children the same age.
How can we compare children from different groups? Let's look at Larry who was a member of our original group of fifth graders. Although the average fifth grader performed 10 push-ups, Larry only completed 6 push-ups. His raw score of 6 converts to a percentile rank of nine (PR=9).
When we compare Larry's performance to all elementary school students, we learn that Larry (a fifth grader) is functioning at the level of the average third grader --- who is also eight years old --- in the ability to do push-ups. Therefore, we see that Larry's age equivalent score is 8 years (AE=8-0) and his grade equivalent score is at the third grade level (GE=3-0).
| Fifth Grade Students: Push Up Scores | ||
|---|---|---|
| Child's Name | Raw Score | Percentile Rank |
| Oscar | 3 | 1 |
| Larry | 6 | 9 |
| Sam | 7 | 16 |
| Amy | 10 | 50 |
| Erik | 13 | 84 |
| Frank | 15 | 95 |
| Nancy | 17 | 99 |
Look at the table above and find Amy. At the time of testing, Amy was 10-0 years old and in the fifth grade. She scored at the mean for her peers, i.e., 10 push-ups. Her grade equivalent score was fifth grade (GE=5-0) and her age equivalent score was 10.0 years (AE=10-0). If we tested a 20 year old person and found that this person was able to do 10 push-ups, then the 20 year old has an age equivalent score of 10-0 and a grade equivalent score of 5.0, i.e., the same score as Amy.
Look again at the table of scores above and find Frank's name. You see that Frank earned a raw score of 15 push-ups which converts to a percentile rank of 95 (PR=95). Frank's score looks great --- until we remember that Frank was "held back" three times. Although he is in the fifth grade, Frank is 13 years old!
With this new information, let's take another look at Franks' performance. The average score for 8th graders (who are 13 years old) is 15. Frank scored 15. Frank had a grade equivalent score of 8th grade (GE = 8.0) and an age equivalent score of 13 years (AE = 13-0). When we compare Frank with other children in his expected grade, we see that his achievement is in the average range. Frank is in the 95th percentile level when compared to fifth graders, not when compared to eighth graders.
Frank's case brings up some additional questions. Frank (age 13) was included in our sample of 5 th graders who had an average age of 10. When compared to this group of children who were younger than him, Frank scored at the 95% percentile rank (PR) level. Question: If we compare Frank's performance to that of children who are three years younger than him, will this comparison provide us with an accurate picture of his physical fitness? Answer: No.
In Frank's case, statistics inform us of two facts. First, we see that Frank performs at a superior level when compared with other children in his grade. Second, we see that he performs at an average level when compared with children who are his age.
When you evaluate the significance of data from tests, you must know how the scores are being reported. Test scores can be reported using percentile ranks, age equivalents, grade equivalents, raw scores, scale scores, subtest scores, or standard scores.
Remember: Although Frank's performance was superior for his grade, it was average for his age. If you did not know Frank's age and grade, you would have been misled as to Frank's actual achievement. But --- if Frank was an 8 year old 3rd grader, his scores would be in the superior range, using both age equivalent and grade equivalent measures.
The number of push-ups each child completed was his or her raw score. Let's assume that we want to obtain an overall fitness score. To obtain an overall or composite score, we will measure three skills (sit-ups, push-ups, a timed 50 yard dash) and obtain scores on each of these skills. In educational testing, the child's overall score (in reading, math, etc.) is often a composite of several subtest scores.
Next, we will develop a weighting system that will convert each child's raw score to a scale score. After we convert the raw scores to scale scores, we will be able to compare each of the three scores to each other (number of push-ups, number of sit-ups, seconds to complete the 50 yard dash). How do we convert raw scores into scale scores?
One way to convert scores is by developing a rank order system. In rank order scoring, the child who scores highest in an event (most push-ups, most sit-ups, fastest run) receives a scale score of 100; the lowest receives a score of 1. The other 98 children receive their respective "rank" as their scale score.
After each child's raw scores are converted to scale scores, we can easily compare an individual child to the group and to all children who are the same age or in the same grade. We can also compare an individual child's performance at different times, i.e. before and after completing the fitness course. Was the child able to do significantly more push-ups after taking the fitness course? Was the child reading better after receiving reading remediation?
Composite Scores
You can see that after we develop a global composite score, the individual child's raw scores on each of the three fitness subtests have less significance. This is exactly what happens with educational achievement and psychological tests. Most educational tests are composites of several subtests; the subtest scores are combined to develop composite scores. More about this shortly.
Let's look at how composite scores can be used and some of the problems that arise when we rely on them.
John is a member of our original group of 100 fifth graders. He has good muscular strength (he scored at the 70% PR level in push-ups and at the 78% PR in sit-ups). But, John is very slow and uncoordinated. In the 50 yard dash, he finished 2nd from the last out of the 100 children (PR=2).
How will John's composite fitness score be derived? In this example, we will average John's percentile rank scores on the three events. John's composite score is determined as follows: Add the percentile ranks of each event (70 + 78 + 2 = 150), then divide this score by the number of events (3). In John's case, 150 / 3 = 50. (Note: actually it is improper to average the percentile rank scores, you must use the standard scores or scale / subtest scores.)
John's composite score is 50. This composite percentile rank score of 50 places him squarely in the "average" range. Is John an "average" child? His individual scores demonstrated a significant amount of subtest scatter. When you analyze his three subtest scores, you see that he has specific strengths and a very severe deficiency. Despite his average composite score, John is not an average child! (Note: As noted above, the proper calculation is to use the standard scores. Thus the same analysis of John's composite score by using standard scores, is calculated to a standard score of 96.5 and percentile rank of 41 --- again, John appears to be an average child).
Let's look at another example of composite scores to see how they can mislead us. Oscar was at the 1 percent level in push-ups. But when the other fitness subtests were given, Oscar was the fastest child in the class scoring at the 99% level. He was average in sit-ups, scoring at the 50% level. Oscar's composite fitness score, using percentile ranking, is 50%. Is Oscar really an average child? Would he benefit from remediation to improve his upper body strength, as measured by push-ups? Oscar also a great deal of subtest scatter, i.e., from extremely weak upper body strength to superior speed.
Subtest Scatter
When subtest scores vary a great deal, this is called subtest scatter. If significant scatter exists, this suggests that the child has areas of strength and weakness that need to be explored.
How can you determine if significant subtest scatter is present? Most subtests have a mean score of 10. Most children will score + or - 3 points away from the mean of 10, i.e. most children will score between 7 and 13.
If the mean on a subtest is 10 (and most children score between 7 and 13), then scores between 9 and 11 will represent minimal subtest scatter. Lets assume that Child A is given a test that is composed of 10 subtests. The child's scores on the 10 subtests are as follows: on 4 subtests, the child scores 10, on 3 subtests, the child scores 9, and on 3 subtests, the child scores 11. In this case, the overall composite score is 10 and the scatter is very minimal. This child scored in the average range in all 10 subtests.
In our next example, we will assume that Child B earns 4 subtest scores of 10, 3 scores of 4, and 3 scores of 16. The child did extremely well on 3 tests, very poorly on 3 tests, and average on 4 subtests. Again, the child's composite score would be 10. Subtest scatter is the difference between the highest and lowest scores. In this case, subtest scatter would be 12 (16-4 = 12) Is this an "average" child? Because the child's scores demonstrate very significant subtest scatter, we need to know more about these weak and strong areas.
In educational situations, it is essential that parents understand the nature of the weak areas, what skills need to be learned to strengthen those areas, and how the strong areas can be used to help remediate the child's weak areas. The spread or variability between the subtest scores is called subtest scatter.
Apply Your Knowledge: Composite Scores & Subtest Scatter in the Wechsler Intelligence Scale for Children-IV (WISC-IV)
How do composite scores and subtest scatter relate to the information contained in your child's evaluations? The results of educational tests given to children are often provided in composite scores.
The Wechsler Intelligence Scale for Children, Fourth Edition (WISC-IV) is the mostly commonly administered test of ability. The WISC-IV includes ten core subtests and five supplementary subtests. Each subtest measures a different ability.
Psychologists typically provide five scores: a Full Scale IQ (FSIQ) and four Index Scores - a Verbal Comprehension Index (VCI), a Perceptual Reasoning Index (PRI), a Working Memory Index (WMI), and a Processing Speed Index (PSI). Index Scores are composites of two or three subtest scores. The Full Scale IQ is a composite score that includes ten of the fifteen WISC-IV subtests.
IQ and Index Scores between 90 and 110 are considered within the "average range." If there is a significant difference between Index scores or if there is significant scatter between subtests, the Full Scale IQ may not accurately represent the child's level of functioning.
Katie is the 14 year old youngster whose situation was outlined earlier in this article. Let's look at her scores on the subtests.
On the Wechsler Intelligence Scale for Children-IV, Katie achieved a Full Scale IQ of 101. If the only number you had was her Full Scale IQ score, you would probably assume that an IQ of 101 placed her squarely in the "average range" of intellectual functioning.
Is Katie an "average" child?
| Katie's Subtest Scores on the Wechsler Intelligence Scale for Children, 4th Edition (WISC-IV) | |||
|---|---|---|---|
| Standard Score or Scaled Score | Standard Score or Scaled Score | ||
| WISC-IV Full Scale IQ | 101 | ||
| Verbal Comprehension Index | 124 | Perceptual Reasoning Index | 88 |
| Similarities | 16 | Block Design | 11 |
| Vocabulary | 14 | Picture Concepts | 7 |
| Comprehension | 12 | Matrix Reasoning | 6 |
| Information | (13) | Picture Completion | (8) |
| Word Reasoning | (12) | ||
| Working Memory Index | 110 | Processing Speed Index | 75 |
| Digit Span | 14 | Coding | 4 |
| Letter-Number Sequencing | 10 | Symbol Search | 7 |
| Arithmetic | (8) | Cancellation | (8) |
Remember: A Full Scale IQ score is a composite of four Index Scores (VCI, PRI, WMI, and PSI). When you look at Katie's scores, you see that she has significant subtest scatter, from a high of 16 on the Similarities subtest (98th percentile) to a low score of 4 on Coding (2nd percentile). By using the Conversion Table below, you can convert the rest of her subtest scores.
There are also significant differences between Katie's Index Scores. Her Verbal Comprehension Index Score (VCI) is 124 (95th percentile), while her Perceptual Reasoning Index Score (PRI) is 88 (21st percentile). When you subtract Katie's Perceptual Reasoning Index Score (PRI) of 88 from her Verbal Comprehension Index Score (VCI) of 124, you find a 36 point difference between these Index Scores.
And, when you subtract her score on the Perceptual Reasoning Index - 21st percentile from her score on the Verbal Comprehension Index - 95th percentile. you see that a difference of 74 points in her percentile ranks (95-21=74) on the Index Scores.
If we rely on composite Index Scores or Full Scale IQ scores, we may easily be misled, with serious consequences. If we did not examine the subtest scores and Index Scores, we might view Katie as an "average" child - and we would be mistaken.
We will look at more of Katie's test scores shortly.
Woodcock-Johnson Tests of Achievement (WJ-III ACH)
One of the most commonly administered individual educational achievement tests is the Woodcock Johnson III Tests of Achievement (WJ-III ACH). The Woodcock-Johnson III Tests of Achievement include two batteries, a standard battery and an extended battery. Subtests are organized into clusters.
Because the WJ-III subtests are short, many do not provide good qualitative information about what a child knows, can do, and where the child needs continued work. For example, the WJ-III does not measure the child's ability to write a paragraph or an essay; it only examines the ability to formulate brief responses.
The WJ-III is scored by computer. The results obtained are organized into cluster scores. Cluster scores must be considered with caution when there is a significant difference between individual subtest scores. Relying on composite or 'cluster' scores can lead to faulty educational decision-making that have tragic consequences for children.
Tip: Parents must obtain all subtest scores on the tests that have been administered on their child and examine subtest scores and Index Scores.
When Apparent Progress Means Actual Regression
One concern that many parents share is the belief that their child is not making adequate progress in a special education program. How can parents know if their perception is accurate? How can parents persuade school officials that the special education program being provided needs to be changed?
Earlier in this article, we discussed how statistics are used in medical treatment planning. We demonstrated how a medical problem is identified and the efficacy of treatment is measured by the use of objective tests. In our example, the patient had pre- and post- testing to determine if the intervention was working. Based on post test results, more medical decisions would be made --- to continue, terminate, or change the treatment plan.
This practice of measuring change, called pre- and post- testing, is essential to educational planning. The child's levels of performance are measured. An educational plan (IEP) is developed and implemented. The child is re-tested at set intervals to determine if the child is progressing, regressing, or maintaining the same position within the group (stagnating).
When we use pre- and post-testing, we can measure educational benefit (or lack of educational benefit). We can use scores from pre- and post- testing to create graphs to visually demonstrate the child's progress or lack of progress in any academic area.
To see how this works, let's visit our fifth grade fitness class. According to earlier testing in September, Erik completed 13 push-ups which placed him in the 84th percentile of all youngsters in his class. After a year of fitness training, fifth graders were re-tested. When Erik was re-tested, he completed 14 push-ups.
Question: Did Erik progress?
Answer: Yes and no.
The average performance of the fifth grade class improved by 2 push-ups, from an average raw score of 10 to 12. Erik's raw score increased by 1 push-up, from 13 to 14. We see that while Erik's age equivalent and grade equivalent scores increased slightly from earlier testing, his actual position in the group dropped from the 84th percentile to the 75th percentile. While Eric is still ahead of his peers, he regressed.
What about Sam? Sam's performance also improved, from a raw score of 7 to 8. Although Sam's age equivalent and grade equivalent scores increased slightly, he also regressed. He dropped from the 16th percentile to the 9th percentile. Sam continues to fall further behind the peer group.
Assume that we test Sam again, when he re-enters school in the fall. Now, we have three sets of test data (beginning 5th grade, end 5th grade, beginning 6th grade). Did Sam's score change? If his percentile continues to fall, Sam continues to regress. We need to know how long will it take for Sam to recoup the skills he lost during the summer. Regression and recoupment are two of the issues considered when determining if the child needs Extended School Year (ESY) services during the summer.
Norm Referenced and Criterion Referenced Tests
Most standardized tests are norm referenced or criterion referenced.
When we evaluated our group of fifth graders, we compared each child's performance to the norm group of fifth graders. Both Erik (raw score of 13, percentile rank of 84) and Sam (raw score of 7, percentile rank of 16) were compared to this norm group of fifth graders. To evaluate benefit, we looked at the norm group and the individual child's position in that group when we administered the first and second tests. We computed each child's change in position to determine progress or regression.
In our example, we also referenced the criteria of number of push-ups completed. A criterion reference analysis determines whether or not a child meets certain criteria (without reference to a norm group.) For example, at the beginning of the year, Sam completed 7 push-ups. If the criteria for success was 8 push-ups, Sam failed to reach that goal. Assume that Sam received a year of physical fitness remediation. After that year, Sam completed 8 push-ups. Does Sam met the criteria for success? The answer to this question depends on whether the criteria increased because Sam is a year older.
Another factor complicates this picture. We know that Sam's' peer group completed 10 push-ups at the beginning of the year and 12 push-ups at the end of the year. Definitions of success are affected by the passage of time. If we rely on criterion referenced measures, we can be misled as to whether the child is falling further behind the peer group. We need to know exactly what the criterion is and what this means when the child is compared to a norm group.
Standard Deviation
Percentile ranks are computed by determining the mean score and the amount of variation of all scores around the mean score. Are the scores bunched around the number 10 in a tight uniform distribution? Are the scores evenly distributed? Do they peak and taper slowly, or do they bunch at the ends, without few or no scores in the middle? Is there a great variance, with the scores spread over a wide range, with two or more peaks? Is there a normal bell curve distribution of scores?
On our push-up test, most of the 5th graders earned scores around 10 push-ups, with an even distribution above and below 10 push-ups. If one-half of the children completed 5 push-ups, one-fourth completed 14 push-ups, and one-fourth completed 16 push-ups, the average or mean number of push-ups would still be 10! One-half of the children scored above 10 and one-half below 10.
In this case, the scores are not evenly distributed in a smooth curve above and below the mean score of 10. The variance is very large and would present a very unusual curve with a peak at 5, a drop to zero between 6 and 13, a jump at 14, a drop at 15, another jump at 16. This distribution of scores would not present a normal bell curve distribution.
Educational and psychological tests are designed to present normal bell curve distributions with predictable patterns of scores. We need to know the mean and standard deviation of the test. In most educational and psychological tests, the mean is 100 and the standard deviation is 15. (Mean = 100, SD = 15) On most subtests, the mean is 10; the standard deviation is 3. (Mean = 10, SD = 3) Average scores do not deviate far from the mean. When a score falls significantly above or below the mean, it is referred to as being a distance from the mean, e.g., 1 or 2 standard deviations from the mean.
In all tests, the mean is 0 (zero) standard deviations from the mean. The next marker on the bell curve is +1 and -1 standard deviations from the mean, followed by 2 standard deviations from the mean. To interpret your child's test scores, you need to know the mean and standard deviation.
Using our original push-up example, the mean was 10 push-ups. The standard deviation (SD) was 3 push-ups. This push-up example is identical to the subtest scores in almost all standardized educational and psychological testing.
One standard deviation above the mean is 10 plus 3, i.e. 10 + 3 = 13. One standard deviation below the mean is 10 minus 3; i.e. 10 - 3 = 7. One standard deviation above the mean always falls at the 84 percentile (PR = 84); one standard deviation below the mean is always at the 16 percentile (PR = 16). Two SD's above the mean is always at the 98 percentile (PR = 98); and two SD's below the mean are always at the 2nd percentile(PR = 2).
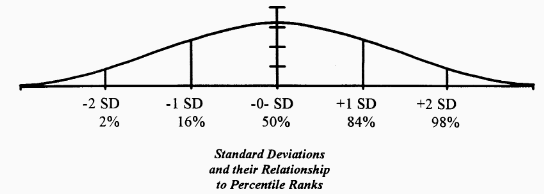
When we look at actual test scores, we see that the child scored "one standard deviation below the mean" on a particular test or subtest. If the score is one standard deviation below the mean, the child's percentile rank is 16.
REMEMBER : Most subtests have a mean of 10 and standard deviation of 3. If a child scores 7 on a subtest, this score is at the 16th percentile. A subtest score of 13 is at the 84th percentile.
Standard Scores
One of the most difficult concepts for most people to grasp is standard scores. Since educational test scores are usually provided in standard scores, parents must know what they mean.
At an IEP meeting, a parent is told that the child earned a standard score of 85 in one area, a standard score of 70 in another area. Most parents are relieved to hear this news. Why? Most parents believe these numbers are similar to grades, with 100 as the highest score and 0 as the lowest. Standard scores are NOT like grades.
With standard scores, the average score or mean is 100. The standard deviation is 15. The average child earns a standard score of 100. If a child scores 1 standard deviation above the mean, the standard score is 100 plus 15; i.e. 100 + 15 = 115. If the child scores 1 standard deviation below the mean, this is 100 minus 15, i.e. 100 - 15 = 85.
A standard score of 115 is 1 standard deviation above the mean so it is always at the 84th percentile. A standard score of 85 is 1 standard deviation below the mean so it is always at the 16th percentile. A standard score of 130 (+2 SD) is always at the 98th percentile. A standard score of 70 (-2 SD) is always at the 2nd percentile.
Remember Katie? Earlier, we learned that on the Wechsler Intelligence Scale, Katie earned a Full Scale IQ of 101. Later, we realized that this score was misleading because Katie's Verbal Comprehension Index Score (VCI) was 124, while her Perceptual Reasoning Index Score (PRI) was 88. The psychologist found that Katie scored 2 standard deviations above the mean on the Similarities subtest of the Wechsler Intelligence Scale for Children, 4th Edition (WISC-IV). What does this mean?
You learned that a score of 2 standard deviations above the mean places the child at the 98th percentile in the area being measured. Since the Similarities subtest of the WISC-IV measures verbal reasoning ability, Katie's verbal reasoning power is at the 98 percentile.
The psychologist also found that Katie had a standard score of 68, 2.5 standard deviations below the mean, on the spontaneous writing sample of the Test of Written Language (TOWL-3). Two SD's below the mean is at the 2nd percentile. With your new knowledge, you know that Katie's ability to produce spontaneous writing samples was actually below the 1st percentile.
When we first introduced Katie, we posed two questions:
1. Do these two test scores help to explain the academic problems Katie is having?
2. Do her test scores tell us anything about her moodiness and her intense dislike of school?
Katie's verbal reasoning ability places her at the 98th percentile of youngsters her age. However, her ability to convey her thoughts in writing is below the 1st percentile. Katie is very bright but she is unable to convey her knowledge to her teachers on written assignments and tests. Would you expect her to feel frustrated and stupid? Do you question why, after years of frustration, Katie is angry, depressed and now wants to quit school?
Wrightslaw Quick Rules of Tests
All educational and psychological tests that report scores using percentile ranks or standard scores are based on the bell curve. To interpret tests results, you must know the mean and the standard deviation. Most standardized tests use a mean of 100 and a standard deviation of 15.
- When educational and psychological tests use standard scores (SS) with a mean of 100 and a standard deviation of 15, a standard score of 100 is at the 50% percentile (PR). A standard score of 85 is at the 16th percentile (PR=16) A standard score of 115 is at the 84th percentile (PR=84).
- When educational and psychological tests use subtest scores with a mean of 10 and standard deviation of 3, a subtest score of 10 is at the 50th percentile (PR=50).
- A subtest score of 7 is at the 16th percentile; a subtest score of 13 is at the 84th percentile (PR=84).
- A standard score of 100 is at the 50th percentile level. One-half of children will fall above and one- half will fall below the mean at the 50th percentile which is represented as a standard score of 100.
- Two-thirds of children will score between + 1 and - 1 standard deviations from the mean.
- Two-thirds of children will score between the 16% and 84% percentile ranks. (84 minus 16 = 68)
- Half of 68 percent is 34 percent. When you subtract 34 percent from the mean of 50 percent, you have 16 percent. When you add 34 percent to 50 percent, you have 84 percent.
- A standard deviation of -1 is at the 16th percentile. A standard deviation of 0 is at the 50th percentile. A standard deviation is +1 is at the 84th percentile.
- A standard score of 85 is at the 16th percentile. A standard score of 100 is at the 50th percentile. A standard score of 115 is at the 84th percentile.
- A standard deviation of -2 is at the 2nd percentile. A standard deviation of +2 is at the 98th percentile.
- A standard score of 70 is at the 2nd percentile. A standard score of 130 is at the 98th percentile. .
- A standard score of 90 is at the 25th percentile. A standard score of 110 is at the 75th percentile. .
- One-half (50 percent) of children will score between the 75th and 25th percentile. (75-25 = 50)
- One half (50 percent) of children will have standard scores between 90 to 110.
- A percentile rank score between 25% and 75% is the same as a standard score of between 90 to 110, which is within the "average range."
The results of most educational tests are reported as standard scores. Parents must learn how to convert standard scores into percentile ranks. By using the conversion table and the bell curve, you can convert any standard score into a percentile rank. The earlier push-up example used standard scores. Click here to view the table
Means and Standard Deviations of Other Tests
With some tests, scores are reported differently. For example, test scores may be reported as "z scores." Z scores are have a mean of 0 (zero) and and standard deviation of 1 (Mean = 0, SD = 1)
If you know that a child earned a z score of -1, you know that the child scored one standard deviation below the mean. One standard deviation below the mean is at the 16th percentile. If you convert this score into the standard score format, with a mean of 100 and a standard deviation of 15, a z score of -1 is the same as a standard score of 85.
Other tests report results as T Scores. T scores have a mean of 50 and a standard deviation of 10 (Mean =50; SD=10). A T score of 60 is the same as a z score of +1. A child who has a T score of 60 or a Z score of +1 scored at the 84th percentile rank. A T score of 70 is the same as a z score of +2, a standard score of 130, and a percentile rank of 98.
A few tests report results in Stanines. In Stanine tests, the mean is five and the standard deviation is 2 (Mean = 5; SD=2).
Applying Your Knowledge to Subtests
Since tests are always in a state of change with new editions being published, we will not attempt to review and describe tests in this article. Please check the links at the end of this article for test information.
Earlier, you learned that Index Scores are actually composites or averages of two or three different subtests. Each subtest measures different abilities. Let's take look at Katie's subtest scores to see what we can learn from them.
| Katie's Subtest Scores on the Wechsler Intelligence Scale for Children, 4th Edition (WISC-IV) | |||
|---|---|---|---|
| Standard Score or Scaled Score | Standard Score or Scaled Score | ||
| WISC-IV Full Scale IQ | 101 | ||
| Verbal Comprehension Index | 124 | Perceptual Reasoning Index | 88 |
| Similarities | 16 | Block Design | 11 |
| Vocabulary | 14 | Picture Concepts | 7 |
| Comprehension | 12 | Matrix Reasoning | 6 |
| Information | (13) | Picture Completion | (8) |
| Word Reasoning | (12) | ||
| Working Memory Index | 110 | Processing Speed Index | 75 |
| Digit Span | 14 | Coding | 4 |
| Letter-Number Sequencing | 10 | Symbol Search | 7 |
| Arithmetic | (8) | Cancellation | (8) |
* Wrightslaw Note: Scores in Brackets ( ) are supplementary subtests. They are not used to calculate the Full Scale IQ or Index Scores.
When we presented Katie's test results, you learned that variation among subtest scores (subtest scatter) is a valuable source of information. Look at Katie's WISC-IV Index and subtest scores in the table above. You can see that she has significant subtest scatter, from a high score of 16 on Similarities (98th percentile) to a low score of 4 on Coding (2nd percentile).
Subtests of the WISC-IV range from a low score of 1 to a high score of 19. WISC-IV subtest scores have a mean of 10 and a standard deviation of 3. A subtest score of 7 is one standard deviation below the mean (-1 SD). By using the Conversion Table, you can convert the subtest score of 7 to a percentile rank of 16 (PR = 16). You can also convert the subtest score of 7 to a standard score of 85.
When you look at Katie's subtest scores, you see that she has significant subtest scatter, from a high score of 16 on the Similarities subtest (98th percentile) to a low score of 4 on the Coding subtest (2nd percentile). You know that subtest scatter is the difference between the highest and lowest subtest scores. Subtract the lowest score of 4 (Coding) from her highest score of 16 (Similarities). Katie's subtest scatter is 12 (16 - 4 = 12). The WISC-IV manual tells us that scatter this great is unusual.
You need to understand what subtests measure. When we first discussed Katie's test scores, you learned that Similarities subtest is highly correlated with abstract reasoning. The Coding subtest measures
visual-perceptual mechanics. Assessment experts Jerome Sattler and Ron Dumont (information is at the end of this article) describe the Coding subtest as "an information processing task that involves the discrimination and memory of visual pattern symbols."
If you find that a child has a visual, hearing, attention, or motor problem that may interfere with his or her ability to take one or more of the subtests, do not use these subtests in computing Index scores or a Full Scale IQ score. A left handed child may be penalized on the Coding subtest because the child will "have to lift his hand repeatedly during the task to view" the test items.
Katie's scores are evidence that she could excel in discussions of complex literature in an honors English class because of her reasoning abilities, but she is unable to write what she knows. Since Katie cannot write what she knew, she was placed in slow-paced remedial classes. Because her abilities were untapped, Katie concluded that she was stupid and wanted to quit school.
When you look at Katie's subtest scores, you see that several scores are in parentheses. On the WISC-IV, Information, Word Reasoning, Arithmetic, Picture Completion, and Cancellation are not included in the Full Scale IQ or the Index Scores. These subtests are used to provide additional data about how a child learns.
Subtests of the Wechsler Intelligence Scale for Children-IV (WISC-IV)
The WISC-IV Technical and Interpretive Manual describes the WISC-IV subtests as follows:
WISC-IV Subtests
Indexes & Subtests Ability Measured Verbal Comprehension Index Similarities Abstract reasoning, verbal categories and concepts Vocabulary Language development, word knowledge, verbal fluency Comprehension Social and practical judgment, common sense Information (supplementary) Factual knowledge, long-term memory, recall Word Reasoning (supplementary) Verbal comprehension, general reasoning ability Working Memory Index Digit Span Short-term auditory memory, mental manipulation Letter-Number Sequencing Sequencing, mental manipulation, attention Arithmetic (supplementary) Attention and concentration, numerical reasoning Perceptual Reasoning Index Block Design Spatial analysis, abstract visual problem solving Picture Concepts Abstract, categorical reasoning Matrix Reasoning Pattern recognition, classification, analogical reasoning Picture Completion (supplementary) Alertness to detail, visual discrimination Processing Speed Index Coding Visual-motor coordination, speed, concentration Symbol Search Visual-motor quickness, concentration, persistence Cancellation (supplementary) Processing speed, visual selective attention, vigilance
Psycho-Educational Evaluations by Evaluators in the Private Sector
We find that public school evaluators are often limited in the tests that are available for their use. Heavy workloads may prevent them from completing a comprehensive evaluation of a child. As a result, we do not rely on testing by public school employees. Instead, we have the child evaluated by a child psychologist, school psychologist, speech language pathologist, and/or educational diagnostician in the private sector.
A Word About Individualized Education Programs (IEPs)
When you use this article and Wrightslaw: Special Education Law, Second Edition, you will be able to write IEP's that include measurable goals.
After you master the information in this article, you will be able to convert test scores into easily understood numbers. You will be able to measure and monitor your child's educational progress. The feelings of helplessness and confusion you have experienced at school meetings will dissipate. You will be knowledgeable about your child's test scores and the significance of the data.
As Susan Bruce learned, "the numbers don't lie." To learn how Susan used information from this article and Wrightslaw: Special Education Law to get quality special education programs for her children, read Success Story: From Victim to a Mighty Force.
The Parent's "To-Do List"
1. After you complete this article, make a list of all the times when your child has been tested. Arrange your list in chronological order. Include the names, dates, and scores of each test that has been administered to your child more than once.
2. Begin your list with the test or tests that have been administered most frequently. In many cases, that will be the Wechsler Intelligence Test and the Woodcock-Johnson and/or Kaufmann Educational Achievement Tests.
3. Write down all of the scores from the first administration of a test battery. Convert these scores to percentile ranks. Complete the same process with the most recent testing of the same battery. Compare the results. You should be able to determine whether your child is being remediated (catching up), staying in the same position, or falling further behind the peer group.
4. Dig for the standard scores or percentile rank scores in your child's file. You may find that some scores are only reported in "ranges" (i.e., high- average, low-average) or in grade equivalent or age equivalent scores. If the standard scores are not available, you should ask for them. When you request the data in standard score format, the school staff may be surprised but they should be able to comply with your request.
5. Take the most glaring deficiencies where your child has shown minimal progress or even regression and chart out the test results. If you do not have a computer, use graph paper. Software programs like Excel and PowerPoint allow for dramatic visual presentations of test data. If this is too difficult or confusing, consult with an expert.
Gather your material --- your bell curve chart and standard score / percentile rank chart, your list of test scores, and your child's evaluations, and consult with a private sector psychologist or educational diagnostician who can explain the significance of the scores using percentile ranks.
6. Ask the professional to use the bell curve chart that includes standard scores, standard deviations and percentile ranks. Be sure that you have a photocopy of the bell curve so you can take it home to study. If the professional is willing, it may be helpful to tape record this portion of the session so that you can go back over it at home with the test scores in front of you.
7. Contact your state's Department of Education and request all publications about special education and IEPs, along with your state regulations.
8. Download our companion article, "Your Child's IEP: Practical and Legal Guidance for Parents and Advocates."
Resources about Testing
Bell Curve Charts & Percentile Rank / Standard Scores Conversion Charts
Download and print bell curve charts and a list of standard scores, scale / subtest scores, standard deviation and percentile ranks:
https://www.wrightslaw.com/advoc/articles/bellcurve.pdf and https://www.wrightslaw.com/advoc/articles/sscore.table.pdf
Print several copies of both. You will be surprised at how often you refer to them. Make copies for your friends.
Wrightslaw: From Emotions to Advocacy, 2nd Edition - Chapters 10 and 11 teach you about tests and measurements and how to measure progress objectively. From Emotions to Advocacy includes bell curves, charts, graphs, and other visual aides to help you master this subject.
Chapter 12 about SMART IEPs teaches you how to draft IEPs that are Specific, Measurable, use Action words, are Realistic, and Time Specific.
Wrightslaw: All About Tests and Assessments by Melissa Lee Farrall, Ph.D., SAIF, Pamela Darr Wright, MA, MSW, and Peter W.D. Wright, Esq. answers more than 200 questions about the assessment process. You will learn what to expect, how to prepare, and how to find a good evaluator. Learn how to request an evaluation and how to provide parental consent. You will find charts of tests and skills. The charts list tests to evaluate specific problems, the skills your child needs in these areas, and shows which tests measure these skills.
This article was originally published in 1998. It has been revise several times, most recently in January 2022.
