Нернста теорема | это... Что такое Нернста теорема? (original) (raw)

Нернста теорема

Начала термодинамики

Статья является частью серии «Термодинамика».
Нулевое начало термодинамики
Первое начало термодинамики
Второе начало термодинамики
Третье начало термодинамики
Разделы термодинамики
Начала термодинамики
Уравнение состояния
Термодинамические величины
Термодинамические потенциалы
Термодинамические циклы
Фазовые переходы
править

Третье начало термодинамики (теорема Нернста) — физический принцип, определяющий поведение энтропии при абсолютном нуле температуры. Является одним из постулатов термодинамики.

Третье начало термодинамики может быть сформулировано так:

«Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система».

$\lim\limits_{T \to \, 0\, K} \left[S(T,x_2) - S(T,x_1) \right] = 0$

или

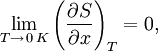
$\lim\limits_{T \to \, 0\, K} \left( \frac{\partial S}{\partial x} \right)_T = 0,$

где x — любой термодинамический параметр.

Заметим, что третье начало термодинамики относится только к равновесным состояниям.

Поскольку на основе второго начала термодинамики энтропию можно определить только с точностью до произвольной аддитивной постоянной (то есть, определяется не сама энтропия, а только её изменение):

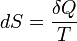$dS = \frac{\delta Q}{T}$ ,

третье начало термодинамики может быть использовано для точного определения энтропии. При этом энтропию равновесной системы при абсолютном нуле температуры считают равной нулю.

Третье начало термодинамики позволяет находить абсолютное значение энтропии, что нельзя сделать в рамках классической термодинамики (на основе первого и второго начал термодинамики). В классической термодинамике энтропия может быть определена лишь с точностью до произвольной аддитивной постоянной _S_0, что практически не мешает большинству термодинамических исследований, так как реально измеряется разность энтропий (_S_0) в различных состояниях. 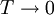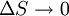Согласно третьему началу термодинамики, при $T\to 0$ значение $\Delta S\to 0$ .

В 1911 году Макс Планк сформулировал третье начало термодинамики, как условие обращения в нуль энтропии всех тел при стремлении температуры к абсолютному нулю: 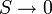$S\to 0$ . Отсюда _S_0 = 0, что даёт возможность определять абсолютное значения энтропии и других термодинамических потенциалов. Формулировка Планка соответствует определению энтропии в статистической физике через термодинамическую вероятность (W) состояния системы S = k_ln_W. При абсолютном нуле температуры система находится в основном квантово-механическом состоянии, если оно невырождено, для которого W = 1 (состояние реализуется единственным микрораспределением). Следовательно, энтропия S при 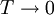$T\to 0$ равна нулю. В действительности при всех измерениях стремление энтропии к нулю начинает проявляться значительно раньше, чем может стать существенной при T = 0 дискретность квантовых уровней макроскопической системы, приводящая к явлениям квантового вырождения.

Из третьего начала термодинамики следует, что абсолютного нуля температуры нельзя достигнуть ни в каком конечном процессе, связанном с изменением энтропии, к нему можно лишь асимптотически приближаться, поэтому третье начало термодинамики иногда формулируют как принцип недостижимости абсолютного нуля температуры. Из третьего начала термодинамики вытекает ряд термодинамических следствий: при 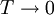$T\to 0$ должны стремиться к нулю теплоёмкости при постоянном давлении и при постоянном объёме, коэффициенты теплового расширения и некоторые аналогичные величины. Справедливость третьего начала термодинамики одно время подвергалась сомнению, но позже было выяснено, что все кажущиеся противоречия (ненулевое значение энтропии у ряда веществ при T = 0) связаны с метастабильными состояниями вещества, которые нельзя считать термодинамически равновесными.

Третье начало термодинамики часто нарушается в модельных системах. Так, при 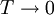$T\to 0$ энтропия классического идеального газа стремится к минус бесконечности. Это говорит о том, что при низких температурах идеальный газ должен вести себя не по уравнению Менделеева — Клапейрона.

Таким образом, третье начало термодинамики указывает на недостаточность классической механики и статистики и является макроскопическим проявлением квантовых свойств реальных систем.

См. также

Литература

Базаров И. П. Термодинамика. М.: Высшая школа, 1991, 376 с.
Базаров И. П. Заблуждения и ошибки в термодинамике. Изд. 2-ое испр. М.: Едиториал УРСС, 2003. 120 с.
Квасников И. А. Термодинамика и статистическая физика. Т.1: Теория равновесных систем: Термодинамика. Том.1. Изд. 2, испр. и доп. М.: УРСС, 2002. 240 с.
Сивухин Д. В. Общий курс физики. — М.: Наука, 1975. — Т. II. Термодинамика и молекулярная физика. — 519 с.
БСЭ

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Нернста теорема" в других словарях:

НЕРНСТА ТЕОРЕМА — установленная нем. физиком В. Нернстом (W. Nernst; 1906) теорема термодинамики, согласно к рой изменение энтропии (DS) при любых обратимых изотермич. процессах, совершаемых между двумя равновесными состояниями при температурах, приближающихся к… … Физическая энциклопедия
НЕРНСТА ТЕОРЕМА — (3 е начало термодинамики): при стремлении температуры к абсолютному нулю энтропия системы стремится к нулю при прочих фиксированных условиях (напр. при неизменных объеме или давлении) (В. Нернст, 1906). Другая формулировка: при помощи конечной… … Большой Энциклопедический словарь
Нернста теорема — то же, что третье начало термодинамики. * * * НЕРНСТА ТЕОРЕМА НЕРНСТА ТЕОРЕМА (3 е начало термодинамики): при стремлении температуры к абсолютному нулю энтропия (см. ЭНТРОПИЯ) системы стремится к нулю при прочих фиксированных условиях (напр., при … Энциклопедический словарь
Нернста теорема — Nernsto teorema statusas T sritis Energetika apibrėžtis Žr. trečiasis termodinamikos dėsnis. atitikmenys: angl. Nernst’s principle; Nernst’s theorem vok. Nernstsches Prinzip, n rus. Нернста теорема, f pranc. principe de Nernst, m … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas
НЕРНСТА ТЕОРЕМА — Нернста принцип, см. Третье начало термодинамики … Большой энциклопедический политехнический словарь
Нернста теорема — установленная В. Нернстом (1906) теорема термодинамики, согласно которой изменение энтропии (См. Энтропия) (ΔS) при любых обратимых изотермических процессах (См. Изотермический процесс), совершаемых между двумя равновесными состояниями… … Большая советская энциклопедия
Теорема Нернста — (тепловая теорема Нернста) утверждение, являющееся одной из формулировок третьего начала термодинамики, сформулированное Вальтером Нернстом в 1906 году как обобщение экспериментальных данных по термодинамике гальванических элементов.… … Википедия
теорема Нернста — третий принцип гидродинамики — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом Синонимы третий принцип гидродинамики EN Nernst theorem … Справочник технического переводчика
Третье начало термодинамики (Нернста теорема) — указывает на поведение энтропии вблизи абсолютного нуля: при стремлении температуры к абсолютному нулю энтропия всех тел также стремится к нулю … Начала современного естествознания
Теорема о равнораспределении — Тепловое движение α пептида. Сложное дрожащее движение атомов, составляющих пептид, случайно, и энергия отдельного атома флуктуирует в широких пределах, но с помощью закона равнораспределения вычисляют как среднюю кинетическую энергию каждого… … Википедия