Пифагоровы тройки | это... Что такое Пифагоровы тройки? (original) (raw)

В математике пифагоровыми числами (пифагоровой тройкой) называется кортеж из трёх целых чисел 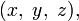(x,\;y,\;z), удовлетворяющих соотношению Пифагора:

_x_2 + _y_2 = _z_2.

Содержание

Свойства

Поскольку уравнение _x_2 + _y_2 = _z_2 однородно, при домножении x, y и z на одно и то же число получится другая пифагорова тройка. Пифагорова тройка называется примитивной, если она не может быть получена таким способом, то есть 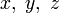x,\;y,\;z — взаимно простые числа.

Треугольник, стороны которого равны пифагоровым числам, является прямоугольным. Кроме того, любой такой треугольник является героновым, то есть таким, у которого все стороны и площадь являются целочисленными. Простейший из них — египетский треугольник со сторонами 3, 4 и 5 (32 + 42 = 52).

Пифагорова тройка 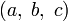(a,\;b,\;c) задаёт точку с рациональными координатами 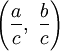\left( \frac a c,\;\frac b c \right) на единичной окружности _x_2 + _y_2 = 1.

Нетрудно видеть, что в примитивной тройке (x,y,z) числа x и y имеют разную чётность. Любая примитивная пифагорова тройка (x,y,z), где x - нечётно, а y - чётно, однозначно представляется в виде 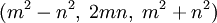(m^2-n^2,\;2mn,\;m^2+n^2) для некоторых натуральных взаимно простых чисел m > n разной чётности. Наоборот, любая такая пара 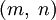(m,\;n) задаёт примитивную пифагорову тройку 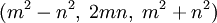(m^2-n^2,\;2mn,\;m^2+n^2). [1]

Примеры

Некоторые пифагоровы тройки (отсортированы по возрастанию максимального числа, выделены примитивные):

(3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (14, 48, 50), (30, 40, 50)…

История

Пифагоровы тройки известны очень давно. В архитектуре древнемесопотамских надгробий встречается равнобедренный треугольник, составленный из двух прямоугольных со сторонами 9, 12 и 15 локтей. Пирамиды фараона Снофру (XXVII век до н. э.) построены с использованием треугольников со сторонами 20, 21 и 29, а также 18, 24 и 30 десятков египетских локтей.

X Всероссийский симпозиум по прикладной и промышленной математике. Санкт - Петербург, 19 мая 2009г.

Доклад: Алгоритм решения Диофантовых уравнений.

В работе рассмотрен метод исследования Диофантовых уравнений и представлены решенные этим методом: - великая теорема Ферма; - поиск Пифагоровых троек и тд. http://referats.protoplex.ru/referats_show/6954.html

См. также

Ссылки

  1. ↑ В. Н. Серпинский Пифагоровы треугольники. — М.: Учпедгиз, 1959. — 111 с.

Wikimedia Foundation.2010.