Плотность измеримого множества | это... Что такое Плотность измеримого множества? (original) (raw)
Плотность измеримого множества
Плотность измеримого множества
Плотность (измеримого) множества E на вещественной прямой 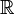 , в точке x ― предел (если он существует) отношения
, в точке x ― предел (если он существует) отношения
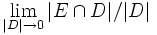
где D ― произвольный отрезок, содержащий x, а | D | ― его мера Лебега. Если вместо меры рассматривать внешнюю меру, то получится определение внешней плотности E в точке x.
Аналогично вводится плотность в _n_-мерном пространстве. При этом длины отрезков заменяются объёмами соответствующих _n_-мерных параллелепипедов с гранями, параллельными координатным плоскостям, а предел рассматривается при стремлении к нулю диаметра параллелепипеда.
Для множеств из 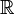 оказывается полезным понятие правой (левой) плотности E в точке x, которое получается из общего определения, если в нём рассматривать лишь отрезки D, имеющие левым (правым) концом точку x.
оказывается полезным понятие правой (левой) плотности E в точке x, которое получается из общего определения, если в нём рассматривать лишь отрезки D, имеющие левым (правым) концом точку x.
Связанные определения
- Точка плотности — точка в которой плотность равна единице.
- Почти все точки измеримого множества суть его точки плотности.
- Точка разрежения — точка в которой плотность равна нулю.
Литература
- Натансон И. П., Теория функций вещественной переменной, 3 изд., М., 1974;
Wikimedia Foundation.2010.
Полезное
Смотреть что такое "Плотность измеримого множества" в других словарях:
- Плотность множества — У этого термина существуют и другие значения, см. Плотность (значения). Связать? … Википедия
- Плотность (значения) — В физике: Плотность веществ: Объемная плотность Относительная плотность Плотность вещества: Плотность нефти Поверхностная плотность Линейная плотность заряда Плотность заряда Плотность тока Плотность потока Оптическая плотность Рентгенологическая … Википедия
- ПЛОТНОСТЬ МНОЖЕСТВА — Е, измеримого на действительной прямой , в точке х предел (если он существует) отношения (1) где D произвольный отрезок, содержащий х, а |D| его длина. Если вместо меры рассматривать внешнюю меру, то получится определение внешней П. м. Ев точке х … Математическая энциклопедия
- Функции множества — функции, сопоставляющие каждому множеству из некоторого класса множеств определённое число. Например, длина отрезка является Ф. м., определённой на классе всех отрезков на прямой (функцией отрезка). Интеграл x) также является… … Большая советская энциклопедия
- ПЛОТНОСТИ ТОЧКА — множества Е в n мерном пространстве точка х, в к рой плотность множества Е равна единице. Если единице равна внешняя плотность, то точка хназ. точкой внешней плотности. П. т. множества является одновременно точкой разрежения для дополнения этого… … Математическая энциклопедия
- ЭРГОДИЧЕСКАЯ ТЕОРИЯ — Введение Э. т. (метрическая теория динамических систем) раздел теории динамических систем, изучающий их статистич. свойства. Возникновение Э. т. (1 я треть 20 в.) было стимулировано попытками доказать эргодическую гипотезу (термин введён П. и Т.… … Физическая энциклопедия
- ГЕОМЕТРИЯ ЧИСЕЛ — геометрическая теория чисел, раздел теории чисел, изучающий теоретико числовые проблемы с применением геометрич. методов. Г. ч. в собственном смысле сформировалась с выходом основополагающей монографии Г. Минков ского [1] в 1896. Исходным пунктом … Математическая энциклопедия
- МАРКОВСКИЙ ПРОЦЕСС — процесс без последействия, случайный процесс, эволюция к рого после любого заданного значения временного параметра tне зависит от эволюции, предшествовавшей t, при условии, что значение процесса в этот момент фиксировано (короче: будущее н… … Математическая энциклопедия
- УПРАВЛЯЕМЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС — случайный процесс, вероятностные характеристики к рого могут изменяться по ходу наблюдений в зависимости от поставленной цели, заключающейся в минимизации (максимизации) того или иного функционала, определяющего качество управления. Различают… … Математическая энциклопедия