Формальное исчисление | это... Что такое Формальное исчисление? (original) (raw)

Формальное исчисление

Форма́льная (аксиоматическая) тео́рия, формальное исчисление — это понятие, разработанное в рамках формальной логики в качестве основы для формализации теории доказательства. Формальная теория — разновидность дедуктивной теории, где множество теорем выделяется из множества формул путем задания множества аксиом и правил вывода.

Определение

Формальная теория 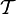$\mathcal{T}$ — это:

конечное множество 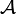$\mathcal{A}$ символов, образующих алфавит;
конечное множество 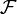$\mathcal{F}$ слов в алфавите 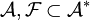$\mathcal{A}, \mathcal{F}\sub \mathcal{A}^*$ , которые называются формулами;
подмножество 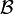$\mathcal{B}$ формул, 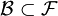$\mathcal{B}\sub \mathcal{F}$ , которые называются аксиомами;
множество 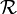$\mathcal{R}$ отношений 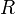$R\,\!$ на множестве формул, 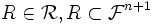$R \in \mathcal{R}, R \sub \mathcal{F}^{n+1}$ , которые называются правилами вывода.

Множество символов 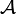$\mathcal{A}$ может быть конечным или бесконечным. Обычно для образования символов используют конечное множество букв, к которым при необходимости приписываются в качестве индексов целые числа или выражения.

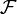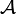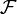Множество формул $\mathcal{F}$ обычно задаётся индуктивным определением, например, с помощью формальной грамматики. Как правило, это множество бесконечно. Множества $\mathcal{A}$ и $\mathcal{F}$ в совокупности определяют язык или сигнатуру формальной теории.

Множество аксиом 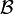$\mathcal{B}$ может быть конечным или бесконечным. Если множество аксиом бесконечно, то, как правило, оно задаётся с помощью конечного числа схем аксиом и правил порождения конкретных аксиом из схемы аксиом. Обычно аксиомы делятся на два вида: логические аксиомы (общие для целого класса формальных теорий) и нелогические или собственные аксиомы (определяющие специфику и содержание конкретной теории).

Множество правил вывода 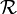$\mathcal{R}$ , как правило, конечно.

См. также

Дедуктивная теория

Литература

Ф. А. Новиков. Дискретная математика для программистов. — СПб.: Питер, 2000. — 304 с.: ил. ISBN 5-272-00183-4.

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Формальное исчисление" в других словарях:

Исчисление предикатов — Логика первого порядка (исчисление предикатов) формальное исчисление, допускающее высказывания относительно переменных, фиксированных функций, и предикатов. Расширяет логику высказываний. В свою очередь является частным случаем логики высшего… … Википедия
Исчисление — У этого термина существуют и другие значения, см. Исчисление (значения) … Википедия
Пи-исчисление — исчисление в теоретической информатике исчисление процессов, изначально разработанное Робином Милнером, Иоахимом Парровом и Дэвидом Уолкером как продолжение работы над исчислением общающихся систем. Целью исчисления является возможность… … Википедия
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ — один из методов математич. анализа, позволяющий в ряде случаев сводить исследование дифференциальных операторов, псевдодифференциалъных операторов и нек рых типов интегральных операторов и решение уравнений, содержащих эти операторы, к… … Математическая энциклопедия
ВЫВОД () — ВЫВОД (в математической логике) В. обычно называется рассуждение, в ходе к рого последовательно получается ряд связанных друг с другом предложений, а также и сама последовательность этих предложений. Нек рые из числа этих предложений не… … Философская энциклопедия
ФОРМАЛЬНАЯ СИСТЕМА — неинтерпретированное исчисление, класс выражений (формул) к рого задается обычно индуктивно – посредством задания исходных ( элементарных , или атомарных ) формул и правил образования (построения) формул, а подкласс доказуемых формул (теорем) –… … Философская энциклопедия
ВЕРОЯТНОСТНАЯ ЛОГИКА — логическая система, в которой высказываниям соответствует непрерывная шкала значений истинности от 0 до 1, причем нуль приписывается высказыванию о невозможном событии, а 1 практически достоверному. В.л. формально можно рассматривать как… … Философская энциклопедия
Формальная система — неинтерпретированное Исчисление, класс выражений (формул) которого задаётся обычно индуктивно – посредством задания исходных («элементарных», или «атомарных») формул и правил образования (построения) формул, а подкласс доказуемых формул… … Большая советская энциклопедия
Разрешимость — В математической логике и теории алгоритмов под разрешимостью подразумевают свойство формальной теории обладать алгоритмом, определяющим по данной формуле, выводима она из множества аксиом данной теории или нет. Теория называется разрешимой, если … Википедия
Неразрешимость — В математической логике и теории алгоритмов под разрешимостью подразумевают свойство формальной теории обладать алгоритмом, определяющим по данной формуле, выводима она из множества аксиом данной теории или нет. Теория называется разрешимой, если … Википедия