Описанная окружность | это... Что такое Описанная окружность? (original) (raw)

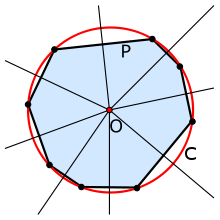
Описанная окру́жность многоугольника — окружность, содержащая все вершины многоугольника. Центром является точка (принято обозначать ) пересечения серединных перпендикуляров к сторонам многоугольника.

Содержание

1 Свойства
2 См. также
3 Примечания
4 Литература

Свойства

Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам. Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).
Около любого правильного многоугольника можно описать окружность, и притом только одну.

Для треугольника

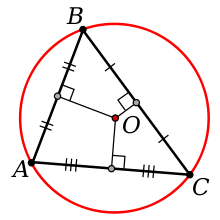
Окружность, описанная около треугольника

Около треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечения серединных перпендикуляров.
У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.
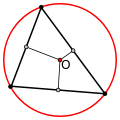
Остроугольный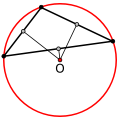
Тупоугольный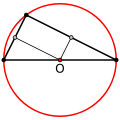
Прямоугольный

Обозначаем буквой О точку пересечения серединных перпендикуляров к его сторонам и проведем отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА = OB = ОС. Поэтому окружность с центром О радиуса ОА проходит через все три вершины треугольника и, значит, является описанной около треугольника ABC.

3 из 4 окружностей, описанных относительно серединных треугольников (образованных средними линиями треугольника), пересекаются в одной точке внутри треугольника. Эта точка и есть центр описанной окружности основного треугольника.
Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.
Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.

Радиус

Радиус описанной окружности может быть найден по формулам

$R = \frac {abc}{4S}$

$R = \frac {a}{2\sin\alpha}$

$R = \frac{abc}{\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}} = \frac{abc}{4\sqrt{p(p-a)(p-b)(p-c)}}$

Где:

a, b, c — стороны треугольника,

$\alpha$ — угол, лежащий против стороны ,

— площадь треугольника.

— полупериметр треугольника.

Положение центра описанной окружности

Пусть $~ {\mathbf r}_A, {\mathbf r}_B, {\mathbf r}_C$ радиус-векторы вершин треугольника, $~ \mathbf{r}_O$ — радиус-вектор центра описанной окружности. Тогда

$~ \mathbf{r}_O= \alpha_A\mathbf{r}_A + \alpha_B\mathbf{r}_B+\alpha_C\mathbf{r}_C$

где

$\alpha_A = \frac{a^2}{8S^2}(\mathbf{r}_A-\mathbf{r}_B,\mathbf{r}_A-\mathbf{r}_C), \qquad \alpha_B = \frac{b^2}{8S^2}(\mathbf{r}_B-\mathbf{r}_A,\mathbf{r}_B-\mathbf{r}_C), \qquad \alpha_C = \frac{c^2}{8S^2}(\mathbf{r}_C-\mathbf{r}_A,\mathbf{r}_C-\mathbf{r}_B)$

При этом a, b, c - длины сторон треугольника, противоположных вершинам A, B, C .

Уравнение описанной окружности

Пусть $~ {\mathbf r}_A = (x_A, y_A), {\mathbf r}_B = (x_B, y_B), {\mathbf r}_C= (x_C, y_C)$ координаты вершин треугольника в некоторой декартовой системе координат на плоскости, $~ \mathbf{r}_O= (x_O, y_O)$ — координаты центра описанной окружности. Тогда

$x_O=\frac{1}{4S}\begin{vmatrix} \end{vmatrix} =0$

Для точек ~(x, y) , лежащих внутри окружности, определитель отрицателен, а для точек вне ее — положителен.

Для четырехугольника

Вписанный простой (без самопересечений) четырёхугольник необходимо является выпуклым.

Около выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180° (π радиан).

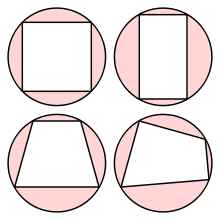
Можно описать окружность около:

любого прямоугольника (частный случай квадрат)
любой равнобедренной трапеции

У четырёхугольника, вписанного в окружность, произведение длин диагоналей равно сумме произведений длин пар противоположных сторон:[1]

|AC|·|BD| = |AB|·|CD| + |BC|·|AD|

Для многоугольника

Если из отрезков составить многоугольник, то его площадь будет максимальна, когда он вписанный.
Если точка равноудалена от вершин многоугольника, то она проектируется в центр окружности, описанной около этого многоугольника.

В сферическом треугольнике

Описанная окружность для сферического треугольника — это окружность, содержащая все его вершины.

Если A, B, C — углы сферического треугольника, P — их полусумма, то тангенс радиуса[2] описанной окружности будет равен[3]:78,83

$\operatorname{tg}R=\sqrt{\frac{-\cos P}{\cos (P-A)\cos (P-B)\cos (P-C)}}\,$

Описанная окружность принадлежит сфере. Радиус, проведенный из центра сферы через центр описанной окружности пересечет сферу в точке пересечения серединных перпендикуляров (больших кругов сферы, перпендикулярных сторонам в их середине) к сторонам сферического треугольника[3]:21-22.

См. также

Примечания

↑ Теорема Птолемея
↑ Здесь радиус окружности измеряется по сфере, то есть представляет собой градусную меру дуги большого круга, соединяющей точку пересечения радиуса сферы, проведенного из центра сферы через центр окружности, со сферой и вершину треугольника.
↑ 1 2 Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — 154 с.

Литература

Элементарная геометрия / Киселёв А.П.. — М.: Просвещение, 1980.
Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 87. — 383 с. — ISBN 5-09-001287-3
Понарин Я. П. Элементарная геометрия. В 2 тт. — М.: МЦНМО, 2004. — С. 53-54. — ISBN 5-94057-170-0