Теорема Биркгофа — Хинчина | это... Что такое Теорема Биркгофа — Хинчина? (original) (raw)

Теорема Биркгофа — Хинчина

Эргодическая теорема Биркгофа — Хинчина утверждает, что для динамической системы, сохраняющей меру, и интегрируемой функции на пространстве для почти всех по этой мере начальных точек соответствующие им временны́е средние сходятся. Более того, если инвариантная мера эргодична, то для почти всех начальных точек предел один и тот же — интеграл функции по данной мере. Этот принцип формулируется как «временно́е среднее для почти всех начальных точек равно пространственному».

Формулировка

Теорема. Пусть $f:X\to X$ -- сохраняющее меру μ отображение, и функция $\varphi$ на X интегрируема по мере μ. Тогда временные средние $\varphi_n(x):=\frac{1}{n}\sum_{j=0}^{n-1} \varphi(f^j(x))$ сходятся к некоторой инвариантной функции $\bar{\varphi}$ :

$\varphi_n(x):=\frac{1}{n}\sum_{j=0}^{n-1} \varphi(f^j(x)) \xrightarrow[n\to\infty]{} \, \bar{\varphi} (x),$

причём сходимость имеет место как в _L_1(X,μ), так и почти всюду по мере μ.

Связь с законом больших чисел

Усиленный закон больших чисел в форме Колмогорова может быть получен как следствие теоремы Биркгофа-Хинчина. А именно, поскольку ясно, что от конкретной реализации случайных величин результат не зависит, можно считать, что вероятностное пространство имеет вид

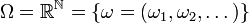$\Omega=\R^{\N}=\{\omega=(\omega_1,\omega_2,\dots)\}$ ,

с мерой 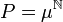$P=\mu^{\N}$ , а случайные величины устроены как ξ_n_(ω) = ω_n_ (мера μ даёт распределение значений любого их ξ_n_). Тогда мера P эргодична относительно левого сдвига — сохраняющего её преобразования

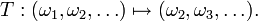
$T:(\omega_1,\omega_2,\dots) \mapsto (\omega_2,\omega_3,\dots).$

С другой стороны, функция 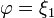$\varphi=\xi_1$ интегрируема по мере P, а 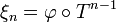$\xi_n=\varphi\circ T^{n-1}$ . Поэтому чезаровские средние 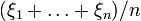$(\xi_1+\dots+\xi_n)/n$ могут быть записаны как временные средние для динамической системы (Ω,P,T):

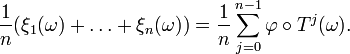
$\frac{1}{n}(\xi_1(\omega)+\dots+\xi_n(\omega)) = \frac{1}{n} \sum_{j=0}^{n-1} \varphi \circ T^j (\omega).$

Поэтому в силу теоремы Биркгофа-Хинчина почти наверняка

$\frac{1}{n}(\xi_1(\omega)+\dots+\xi_n(\omega)) = \frac{1}{n} \sum_{j=0}^{n-1} \varphi \circ T^j (\omega) \xrightarrow[n\to\infty]{} \int_{\Omega} \varphi \, dP = \int_{\R} x \, d\mu(x) = \mathbb{E} \xi_1.$

Это и есть заключение усиленного закона больших чисел.

Литература

А. Б. Каток, Б. Хасселблат. Введение в теорию динамических систем с обзором последних достижений / Пер. с англ. под ред. А. С. Городецкого. М.: МЦНМО, 2005. ISBN 5-94057-063-1

Wikimedia Foundation.2010.