Marching squares | это... Что такое Marching squares? (original) (raw)

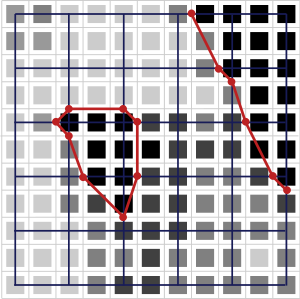
Схематическое изображение алгоритма: цвет квадрата обозначает значение в данной клетке регулярной сетки, чем темнее - тем значение ближе к изолиниям. Красным показаны полученные изолинии.

Marching Squares (англ. движущиеся квадраты) – алгоритм в компьютерной графике, который генерирует изолинии на двухмерном скалярном поле.

Применение

Алгоритм используется при визуализации изобар на картах погоды и горизонталей на географических картах. Является упрощением алгоритма marching cubes для плоского случая.

Принцип работы

На вход алгоритм получает регулярную сетку, в каждом узле которой известно значение поля. Выходная сетка (на рисунке обозначена синим цветом) может иметь меньшее разрешение (в этом случае теряется точность, но уменьшается ступенчатость). Далее для каждого узла выходной сетки проверяется, выше ли значение в нем, чем на изоповерхности. Всем узлам, которые выше, приписывается "+", остальным "–". Далее рассматриваются квадратики выходной сетки, вершины которых лежат в отмеченных узлах. Всего получается 16 различных случаев, которые с учетом симметрий и поворотов можно свести к четырем:

Случай 1: все вершины имеют один знак
Случай 2: у одной вершины знак отличается
Случай 3: вершины с одинаковыми знаками имеют общее ребро
Случай 4: вершины с одинаковыми знаками не имеют общего ребра

В четвертом случае невозможно однозначно определить форму сегмента изолинии, поэтому дополнительно просматривается значение в центре квадрата (если входные данные это позволяют). При невозможности узнать значение в центре квадрата принятое решение может повлиять на связность изолинии.

Случай 1: все вершины находятся выше (или ниже) изоповерхности.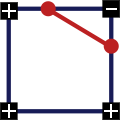
Случай 2: за исключением одной, все вершины находятся выше (или ниже) изоповерхности.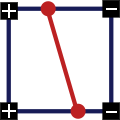
Случай 3: две вершины на одном ребре находятся выше (или ниже) изоповерхности.
Случай 4: две вершины, не имеющие общего ребра, находятся выше (или ниже) изоповерхности.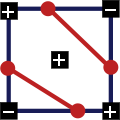
Решение Случая 4 при положительном значении в ячейке.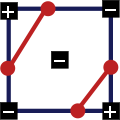
Решение Случая 4 при отрицательном значении в ячейке.

Для улучшения качества получаемой изолинии применяется линейная интерполяция. В таком случае конец сегмента изолинии на ребре квадрата делит ребро в отношении $\frac{f_1-c}{c-f_2}$ , где f_1, f_2 - значения на концах ребра квадрата, - значение изолинии. Фактически, конец сегмента изолинии "подтягивается" к тому концу ребра, который ближе к реальной изолинии.

Ссылки

Реализация на Java
Marching Square Matlab algorithm - An easy to understand open-source marching square algorithm.
Isoline Isoband - Algorithm descriptions and open source C/Fortran code for the AVS scientific visualization system (Mike French, 1992).