Теоремы Гёделя о неполноте | это... Что такое Теоремы Гёделя о неполноте? (original) (raw)

Теоремы Гёделя о неполноте

Теоремы Гёделя о неполноте — две теоремы математической логики о принципиальных ограничениях формальной арифметики и, как следствие, всякой достаточно сильной[1] теории первого порядка.

Первая теорема утверждает, что если формальная арифметика непротиворечива, то в ней существует невыводимая и неопровержимая формула.

Вторая теорема утверждает, что если формальная арифметика непротиворечива, то в ней невыводима некоторая формула, содержательно утверждающая непротиворечивость этой теории.

Эти теоремы были доказаны Куртом Гёделем в 1930 году (опубликованы в 1931) и имеют непосредственное отношение ко второй проблеме из знаменитого списка Гильберта.

Содержание

Первая теорема Гёделя о неполноте

Утверждение первой теоремы Гёделя о неполноте можно сформулировать следующим образом:

Если формальная арифметика S непротиворечива, то в ней существует такая замкнутая формула G, что ни G, ни её отрицание ¬G не являются выводимыми в S_._

Теория, содержащая неразрешимое, то есть невыводимое и неопровержимое, предложение, называется неполной.

При доказательстве теоремы Гёдель построил формулу G в явном виде, иногда её называют гёделевой неразрешимой формулой. В стандартной интерпретации[2] предложение G утверждает свою собственную невыводимость в S. Следовательно, по теореме Гёделя, если теория S непротиворечива, то эта формула и в самом деле невыводима в S и потому истинна в стандартной интерпретации. Таким образом, для натуральных чисел, формула G верна, но в S невыводима.

Доказательство Гёделя можно провести и для любой теории, полученной из S добавлением новых аксиом, например, формулы G в качестве аксиомы. Поэтому любая непротиворечивая теория, являющаяся расширением формальной арифметики, будет неполна.

Для доказательства первой теоремы о неполноте Гёдель сопоставил каждому символу, выражению и последовательности выражений формальной арифметики определенный номер. Поскольку формулы и теоремы являются предложениями арифметики, а формальные выводы теорем являются последовательностями формул, то стало возможным говорить о теоремах и доказательствах в терминах натуральных чисел. Например, пусть гёделева неразрешимая формула G имеет номер m, тогда она эквивалентна следующему утверждению на языке арифметики: "нет такого натурального числа n, что n есть номер вывода формулы с номером m". Подобное сопоставление формул и натуральных чисел называется арифметизацией математики и было осуществлено Гёделем впервые. Эта идея впоследствии стала ключом к решению многих важных задач математической логики.

Набросок доказательства[3]

Зафиксируем некоторую формальную систему PM, в которой можно представить элементарные математические понятия[4].

Выражения формальной системы являются, если смотреть извне, конечными последовательностями примитивных символов (переменных, логических постоянных, и скобок или точек) и нетрудно строго уточнить какие последовательности примитивных символов являются формулами, а какие нет. Аналогично, с формальной точки зрения, доказательства есть ни что иное, как конечные последовательности формул (со строго заданными свойствами). Для математического рассмотрения не имеет значения, какие объекты взять в качестве примитивных символов, и мы решаем использовать для этих целей натуральные числа. Соответственно, формула является конечной последовательностью натуральных чисел, вывод формулы - конечной последовательностью конечных последовательностей натуральных чисел. Математические понятия (утверждения) таким образом становятся понятиями (утверждениями) о натуральных числах или их последовательностях, и, следовательно, сами могут быть выражены в символизме системы PM (по крайней мере частично). Может быть показано, в частности, что понятия "формула", "вывод", "выводимая формула" определимы внутри системы PM, то есть можно восстановить, например, формулу F(v) в PM с одной свободной переменной v (тип которой - числовая последовательность) такую, что F(v), в интуитивной интерпретации, означает: v - выводимая формула. Теперь построим неразрешимое предложение системы PM, то есть предложение A, для которого ни A, ни не-A невыводимы, следующим образом:

Формулу в PM с точно одной свободной переменной, тип которой натуральное число (класс классов), будем называть класс-выражением. Упорядочим класс-выражения в последовательность каким-либо образом, обозначим n-е через R(n), и заметим, что понятие "класс-выражение", также как и отношение упорядочения R можно определить в системе PM. Пусть α будет произвольным класс-выражением; через [α;n] обозначим формулу, которая образуется из класс-выражения α заменой свободной переменной на символ натурального числа n. Тернарное отношение x = [y;z] тоже оказывается определимым в PM. Теперь мы определим класс K натуральных чисел следующим образом:

n ∈ K ≡ ¬Bew[R(n);n] (*)

(где Bew x означает: x - выводимая формула). Так как все понятия, встречающиеся в этом определении, можно выразить в PM, то это же верно и для понятия K, которое из них строится, то есть имеется такое класс-выражение S, что формула [S;n], интуитивно интерпретируемая, обозначает, что натуральное число n принадлежит K. Как класс-выражение, S идентична некоторому определенному R(q) в нашей нумерации, то есть

S = R(q)

выполняется для некоторого определенного натурального числа q. Теперь покажем, что предложение [R(q);q] неразрешимо в PM. Так, если предложение [R(q);q] предполагается выводимым, тогда оно оказывается истинным, то есть, в соответсвии со сказанным выше, q будет принадлежать K, то есть, в соответствии с (*), ¬Bew[R(q);q] будет выполняться, что противоречит нашему предположению. С другой стороны, если бы отрицание [R(q);q] было выводимым, то будет иметь место ¬ n ∈ K, то есть Bew[R(q);q] будет истинным. Следовательно, [R(q);q] вместе со своим отрицанием будет выводимо, что снова невозможно.

Полиномиальная форма

После того, как Юрий Матиясевич доказал диофантовость любого эффективно перечислимого множества, и были найдены примеры универсальных диофантовых уравнений, появилась возможность сформулировать теорему о неполноте в полиномиальной (или диофантовой) форме[5][6][7]:

Для каждой непротиворечивой теории T можно указать такое целое значение параметра K, что уравнение

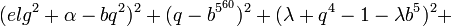
(elg^2 + \alpha - bq^2)^2 + (q - b^{5^{60}})^2 + (\lambda + q^4 - 1 - \lambda b^5)^2 +

(θ + 2_z_ − _b_5)2 + (u + _t_θ − l)2 + (y + _m_θ − e)2 + (n − _q_16)2 +

((g + e _q_3 + l _q_5 + (2(e − _z_λ)(1 + g)4 + λ_b_5 + λ_b_5_q_4)_q_4)(_n_2 − n) +

(_q_3 − b l + l + θλ_q_3 + (_b_5 − 2)_q_5)(_n_2 − 1) − r)2 +

(p − 2_w_ _s_2_r_2_n_2)2 + (_p_2_k_2 − _k_2 + 1 − τ2)2 +

(4(c − k s _n_2)2 + η − _k_2)2 + (r + 1 + h p − h − k)2 +

(a − (w _n_2 + 1)r s n_2)2 + (2_r + 1 + φ − c)2 +

(b w + c a − 2_c_ + 4αγ − 5γ − d)2 +

((_a_2 − 1)_c_2 + 1 − _d_2)2 + ((_a_2 − 1)_i_2_c_4 + 1 − _f_2)2 +

(((a + _f_2(d_2 − a))2 − 1)(2_r + 1 + j c)2 + 1 − (d + o f)2)2 +

(((z + u + y)2 + u)2 + y − K)2 = 0

не имеет решений в неотрицательных целых числах, но этот факт не может быть доказан в теории T_. Более того, для каждой непротиворечивой теории множество значений параметра K, обладающих таким свойством, бесконечно и алгоритмически неперечислимо._

Вторая теорема Гёделя о неполноте

В формальной арифметике S можно построить такую формулу, которая в стандартной интерпретации[2] является истинной в том и только в том случае, когда теория S непротиворечива. Для этой формулы справеливо утверждение второй теоремы Гёделя:

Если формальная арифметика S непротиворечива, то в ней невыводима формула, содержательно утверждающая непротиворечивость S_._

Иными словами, непротиворечивость формальной арифметики не может быть доказана средствами этой теории. Однако существуют доказательства непротиворечивости формальной арифметики, использующие средства, невыразимые в ней.

Набросок доказательства

Сначала строится формула Con, содержательно выражающая невозможность вывода в теории S какой-либо формулы вместе с ее отрицанием. Тогда утверждение первой теоремы Гёделя выражается формулой Con ⊃ G, где G — Гёделева неразрешимая формула. Все рассуждения для доказательства первой теоремы могут быть выражены и проведены средствами S, то есть в S выводима формула Con ⊃ G. Отсюда, если в S выводима Con, то в ней выводима и G. Однако, согласно первой теореме Гёделя, если S непротиворечива, то G в ней невыводима. Следовательно, если S непротиворечива, то в ней невыводима и формула Con.

Примечания

  1. ↑ Грубо говоря, теория K является достаточно сильной, если понятия натурального числа, 0, 1, сложения и умножения можно определить в K таким образом, чтобы аксиомы формальной арифметики оказывались выводимыми в K.
  2. ↑ 1 2 Интерпретация формул теории S называется стандартной, если её областью является множество неотрицательных целых чисел, символ 0 интерпретируется числом 0, функциональные буквы ', +, • интерпретируются прибавлением единицы, сложением и умножением соответственно, предикатная буква = интерпретируется отношением тождества.
  3. ↑ Gödel, Kurt (1931). On Formally Undecidable Propositions of the Principia Mathematica and Related Systems. I. в сборнике Davis, Martin, editor (1965). The Undecidable: Basic Papers On Undecidable Propositions, Unsolvable Problems And Computable Functions. pp. 6–8
  4. ↑ В своих рассуждениях Гёдель использует несколько расширенную систему Фреге и Рассела Principia Mathematica
  5. ↑ Jones J. P., Undecidable diophantine equations
  6. ↑ Martin Davis, Diophantine Equations & Computation
  7. ↑ К. Подниекс, Теорема Геделя в диофантовой форме

См. также

Ссылки

Wikimedia Foundation.2010.