Метод Гаусса — Жордана | это... Что такое Метод Гаусса — Жордана? (original) (raw)

Метод Гаусса — Жордана

Метод Гаусса — Жордана используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе, отыскания ранга матрицы. Метод является модификацией метода Гаусса. Назван в честь К. Ф. Гаусса и немецкого геодезиста и математика Вильгельма Йордана [1].

Алгоритм

Выбирают первую колонку слева, в которой есть хоть одно отличное от нуля значение.
Если самое верхнее число в этой колонке есть нуль, то меняют всю первую строку матрицы с другой строкой матрицы, где в этой колонке нет нуля.
Все элементы первой строки делят на верхний элемент выбранной колонки.
Из оставшихся строк вычитают первую строку, умноженную на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) нуль.
Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.
После повторения этой процедуры n − 1 раз получают верхнюю треугольную матрицу
Вычитаем из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали.
Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).
Чтобы получить обратную матрицу, нужно применить все операции в том же порядке к единичной матрице.

Пример

Для решения следующей системы уравнений:

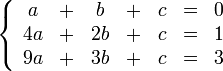
$\left\{\begin{array}{ccccccl} a &+& b &+& c &=& 0\\ 4a &+& 2b &+& c &=& 1\\ 9a &+& 3b &+& c &=& 3 \end{array}\right.$

запишем её в виде матрицы 3×4, где последний столбец является свободным членом:

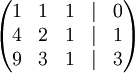
$\begin{pmatrix} 1 & 1 & 1 & | & 0 \\ 4 & 2 & 1 & | & 1 \\ 9 & 3 & 1 & | & 3 \end{pmatrix}$

Проведём следующие действия:

К строке 2 добавим: −4 × Строку 1.
К строке 3 добавим: −9 × Строку 1.

Получим:

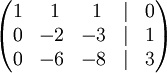
$\begin{pmatrix} 1 &\ 1 &\ 1 & | & 0 \\ 0 & -2 & -3 & | & 1 \\ 0 & -6 & -8 & | & 3 \end{pmatrix}$

К строке 3 добавим: −3 × Строку 2.
Строку 2 делим на −2

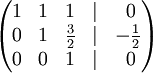
$\begin{pmatrix} 1 & 1 & 1 & | &\ 0 \\ 0 & 1 & {3 \over 2} & | & -{1 \over 2} \\ 0 & 0 & 1 & | &\ 0 \end{pmatrix}$

К строке 1 добавим: −1 × Строку 3.
К строке 2 добавим: −3/2 × Строку 3.

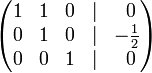
$\begin{pmatrix} 1 & 1 & 0 & | &\ 0 \\ 0 & 1 & 0 & | & -{1 \over 2} \\ 0 & 0 & 1 & | &\ 0 \end{pmatrix}$

К строке 1 добавим: −1 × Строку 2.

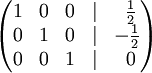
$\begin{pmatrix} 1 & 0 & 0 & | &\ {1 \over 2} \\ 0 & 1 & 0 & | & -{1 \over 2} \\ 0 & 0 & 1 & | &\ 0 \end{pmatrix}$

В правом столбце получаем решение:

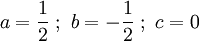$a = \frac{1}{2} \; ; \ b = -\frac{1}{2} \; ; \ c = 0$ .

Ссылки

Lipschutz, Seymour, and Lipson, Mark. "Schaum's Outlines: Linear Algebra". Tata McGraw-hill edition. Delhi 2001. pp. 69-80.

Примеры реализации алгоритма:

Примечания

↑ Транскрипция фамилии как «Жордан» является ошибочной, но она общепринята и встречается в большинстве русскоязычных источников.

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Метод Гаусса — Жордана" в других словарях:

Метод Гаусса-Жордана — используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе, отыскания ранга матрицы. Метод является модификацией метода Гаусса. Назван в честь… … Википедия
Метод Гаусса — Йордана — Метод Гаусса Жордана используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе, отыскания ранга матрицы. Метод является модификацией метода Гаусса.… … Википедия
Метод Гаусса — У этого термина существуют и другие значения, см. Метод Гаусса (оптимизация). Метод Гаусса[1] классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью… … Википедия
Метод Жордана-Гаусса — Метод Гаусса Жордана используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе, отыскания ранга матрицы. Метод является модификацией метода Гаусса.… … Википедия
Метод Жордана — Гаусса — Метод Гаусса Жордана используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе, отыскания ранга матрицы. Метод является модификацией метода Гаусса.… … Википедия
Метод простой итерации — Содержание 1 Постановка задачи 2 Численные методы решения уравнений 2.1 Метод простой итерации … Википедия
Гаусс, Карл Фридрих — У этого термина существуют и другие значения, см. Гаусс. Карл Фридрих Гаусс Carl Friedrich Gauß … Википедия
К. Гаусс — Карл Фридрих Гаусс Carl Friedrich Gauß Дата рождения: 30 апреля 1777 Место рождения: Брауншвейг Дата смерти: 23 февраля 1855 Место смерти … Википедия
Карл Гаусс — Карл Фридрих Гаусс Carl Friedrich Gauß Дата рождения: 30 апреля 1777 Место рождения: Брауншвейг Дата смерти: 23 февраля 1855 Место смерти … Википедия
Карл Фридрих Гаусс — Carl Friedrich Gauß Дата рождения: 30 апреля 1777 Место рождения: Брауншвейг Дата смерти: 23 февраля 1855 Место смерти … Википедия