Экспонента | это... Что такое Экспонента? (original) (raw)

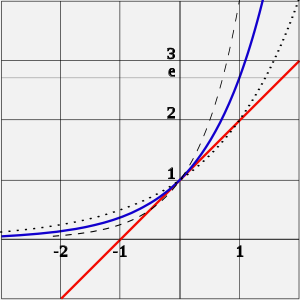
Экспонента — показательная функция \exp(x)=e^x, где e — основание натуральных логарифмов (e = 2.7182818284590452...).

Содержание

Определение

Экспоненциальная функция может быть определена различными эквивалентными способами. Например, через ряд Тейлора:

e^x=\sum_{n=0}^\infty \frac{x^n}{n!}

или через предел:

e^x=\lim_{n\rightarrow \infty} \left( 1+\frac{x}{n} \right)^n

Здесь x — любое комплексное число.

Свойства

Комплексная экспонента

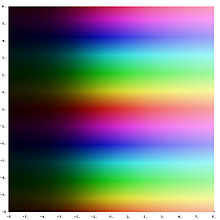
График экспоненты в комплексной плоскости.
Легенда

Комплексная экспонента — математическая функция, задаваемая соотношением f(z)=e^z, где z есть комплексное число. Комплексная экспонента определяется как аналитическое продолжение экспоненты f(x)=e^x вещественного переменного x:

Определим формальное выражение

e^z=e^{x+iy}=e^x\cdot e^{iy}.

Определенное таким образом выражение на вещественной оси будет совпадать с классической вещественной экспонентой. Для полной корректности построения необходимо доказать аналитичность функции e^z, то есть показать, что e^z разлагается в некоторый сходящийся к данной функции ряд. Покажем это:

f(z)=e^z=e^x\cdot e^{iy}=e^{iy}\sum_{n=0}^\infty\frac{x^n}{n!}

Сходимость данного ряда легко доказывается:

\left|e^{iy}\sum_{n=0}^\infty\frac{x^n}{n!}\right|=\left|\sum_{n=0}^\infty\frac{x^n}{n!}\right|\le\sum_{n=0}^\infty\left|\frac{x^n}{n!}\right|=e^{|x|}.

Ряд всюду сходится абсолютно, то есть вообще всюду сходится, таким образом, сумма этого ряда в каждой конкретной точке будет определять значение аналитической функции f(z)=e^z. Согласно теореме единственности, полученное продолжение будет единственно, следовательно, на комплексной плоскости функция e^z всюду определена и аналитична.

Свойства

Вариации и обобщения

Аналогично экспонента определяется для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.

Матричная экспонента

Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:

\exp A=\sum_{k=0}^{\infty} \frac{A^k}{k!}.

Определённый таким образом ряд сходится для любого оператора A с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы A: \exp \|A\|. Следовательно, экспонента от матрицы A \in \Bbb{R}^{n\times n} всегда определена и сама является матрицей.

С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение \dot x=Ax, ~~~ x\in \mathbb R^n с начальным условием x(0)=x_0 имеет своим решением x(t)=\exp (At) x_0.

Обратная функция

Обратной функцией к экспоненциальной функции является натуральный логарифм. Обозначается \ln x\,:

\ln x = \log_{e} x.

См. также

Литература