Механическое равновесие | это... Что такое Механическое равновесие? (original) (raw)

Механи́ческое равнове́сие — состояние механической системы, при котором сумма всех сил, действующих на каждую её частицу, равна нулю и сумма моментов всех сил, приложенных к телу относительно любой произвольно взятой оси вращения, также равна нулю.

В состоянии равновесия тело находится в покое (вектор скорости равен нулю) в выбранной системе отсчета либо движется равномерно прямолинейно или вращается без касательного ускорения.

Содержание

• 1 Определение через энергию системы
• 2 Виды равновесия
  • 2.1 Неустойчивое равновесие
  • 2.2 Устойчивое равновесие
  • 2.3 Безразличное равновесие
  • 2.4 Устойчивость в системах с большим числом степеней свободы

Определение через энергию системы

В механике сплошной среды, где принимается гипотеза сплошности, такое определение неприменимо. К тому же данное определение ничего не говорит об одной из наиболее важных характеристик равновесия — его устойчивости. Поэтому более общее и распространённое определение механического равновесия звучит так: Механическое равновесие — состояние системы, при котором её положение в конфигурационном пространстве находится в точке с нулевым градиентом потенциальной энергии.

Так как энергия и силы связаны фундаментальными зависимостями, это определение эквивалентно первому. Однако определение через энергию может быть расширено для того, чтобы получить информацию об устойчивости положения равновесия.

Виды равновесия

Приведём пример для системы с одной степенью свободы. В этом случае достаточным условием положения равновесия будет являться наличие локального экстремума в исследуемой точке. Как известно, условием локального экстремума дифференцируемой функции является равенство нулю её первой производной. Чтобы определить, когда эта точка является минимумом или максимумом, необходимо проанализировать её вторую производную. Устойчивость положения равновесия характеризуется следующими вариантами:

• неустойчивое равновесие;
• устойчивое равновесие;
• безразличное равновесие.

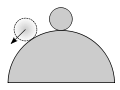
Неустойчивое равновесие

В случае, когда вторая производная отрицательна, потенциальная энергия системы находится в состоянии локального максимума. Это означает, что положение равновесия неустойчиво. Если система будет смещена на небольшое расстояние, то она продолжит своё движение за счёт сил, действующих на систему.

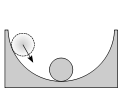
Устойчивое равновесие

Вторая производная > 0: потенциальная энергия в состоянии локального минимума, положение равновесия устойчиво (см. Теорема Лагранжа об устойчивости равновесия). Если систему сместить на небольшое расстояние, она вернётся назад в состояние равновесия. Равновесие устойчиво, если центр тяжести тела занимает наинизшее положение по сравнению со всеми возможными соседними положениями.

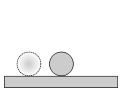
Безразличное равновесие

Вторая производная = 0: в этой области энергия не варьируется, а положение равновесия является безразличным. Если система будет смещена на небольшое расстояние, она останется в новом положении.

• Виды устойчивости
• 
  Неустойчивое равновесие
• 
  Устойчивое равновесие
• 
  Безразличное равновесие

Устойчивость в системах с большим числом степеней свободы

Если система имеет несколько степеней свободы, то может оказаться, что в сдвигах одних направлениях равновесие устойчиво, а в других - неустойчиво. Простейшим примером такой ситуации является "седловина" или "перевал" (в этом месте хорошо бы разместить картинку).

Равновесие системы с несколькими степенями свободы будет устойчивым только в том случае, если оно устойчиво во всех направлениях.