Дельта-функция | это... Что такое Дельта-функция? (original) (raw)

У этого термина существуют и другие значения, см. Дельта (значения).

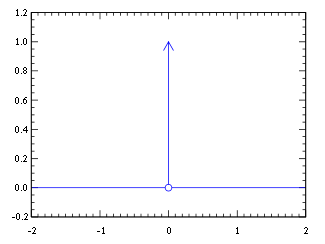
Схематический график одномерной дельта-функции.

Де́льта-фу́нкция (или δ-функция, δ-функция Дирака, дираковская дельта, единичная импульсная функция) — обобщённая функция, которая позволяет записать точечное воздействие, а также пространственную плотность физических величин (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенной или приложенной в одной точке.

Например, плотность единичной точечной массы m, находящейся в точке a для примера, одномерного евклидова пространства $\R^1,$ записывается с помощью $\delta$ -функции в виде $m\delta(x-a).$ Дельта-функция также применима для описания распределений заряда, массы и т. п. на поверхностях или линиях.

$\delta$ -Функция не является функцией в классическом смысле, а определяется как обобщённая функция: непрерывный линейный функционал на пространстве дифференцируемых функций. Можно ввести производную для δ-функции, которая тоже будет обобщённой функцией и интеграл, опеределяемый как функция Хевисайда. Нетрудно указать последовательности обычных классических функций, слабо сходящиеся к $\delta$ -функции.

Можно различать одномерную и многомерные дельта-функции, однако последние могут быть представлены в виде произведения одномерных функций в количестве, равном размерности пространства, на котором определена многомерная функция.

Введена английским физиком Полем Дираком.

Содержание

1 Определения
2 Свойства
3 δ-Функция как слабый предел
4 Интегральное представление
5 Производная дельта-функции
6 Преобразование Фурье
7 Представление многомерных дельта-функций в различных системах координат
8 Физическая интерпретация
9 Примечания
10 Литература
11 См. также

Определения

Существуют различные взгляды на понятие дельта-функции. Получающиеся при этом объекты, вообще говоря, различны, однако обладают рядом общих характерных свойств. Все указанные ниже конструкции естественно обобщаются на случаи пространств большей размерности $(\R^n,\ n>1)$ .

Интуитивное определение

Дельта-функцию (функция Дирака) одной вещественной переменной можно представлять себе как «функцию» $\delta(x)$ , для которой выполняются следующие равенства:

$\delta(x)=\left\{\begin{matrix} +\infty, & x=0, \\ 0, & x\ne 0; \\ \end{matrix}\right.$
$\int\limits_{-\infty}^{+\infty}\delta(x)\,dx=1.$

То есть эта функция не равна нулю только в точке _x_=0, где она обращается в бесконечность таким образом, чтобы её интеграл по любой окрестности _x_=0 был равен 1. В этом смысле понятие дельта-функции аналогично физическим понятиям точечной массы или точечного заряда. Аналогичные условия верны и для дельта-функций, определённых на $\mathbb{R}^n.$

Эти равенства не принято считать определением дельта-функции, однако во многих учебниках по физике она определяется именно так, и этого достаточно для решения физических задач. Отметим, что помимо этого неявно предполагается равенство

$\int\limits_{-\infty}^{+\infty}\delta(x)f(x)\,dx=f(0)$

(фильтрующее свойство) для любой функции f. Оно не следует даже формально из указанного выше тождества, так как, вообще говоря, значение этого интеграла также могло бы включать в себя производные от f. Именно это происходит с производными от дельта-функции, которые также почти всюду равны 0 и обращаются в бесконечность при _x_=0.

Классическое определение

Дельта-функция определяется как линейный непрерывный функционал на некотором функциональном пространстве (пространстве основных функций). В зависимости от цели и желаемых свойств, это может быть пространство функций с компактным носителем, пространство функций, быстро убывающих на бесконечности, гладких функций на многообразии, аналитических функций и т. д. Для того, чтобы были определены производные дельта-функции с хорошими свойствами, во всех случаях основные функции берутся бесконечно дифференцируемыми, пространство основных функций также должно быть полным метрическим пространством. Общий подход к обобщённым функциям см. в соответствующей статье. Такие обобщённые функции также называют распределениями.

Мы рассмотрим самый простой вариант. В качестве пространства основных функций рассмотрим пространство $\mathcal{E}$ всех бесконечно дифференцируемых функций на отрезке. Последовательность $\varphi_n\in\mathcal{E}$ сходится к $\varphi\in\mathcal{E}$ , если на любом компакте $K\in\R$ функции $\varphi_n$ сходятся к $\varphi$ равномерно вместе со всеми своими производными:

$\lim_{n\to\infty}\varphi_n=\varphi\iff\sup_j\sup_{x\in K}\left|\varphi^{(j)}_n(x)\right|\xrightarrow{n\to\infty}\,0.$

Это локально выпуклое метризуемое пространство. Дельта-функцию определим как функционал $\delta\in\mathcal{E}^\prime$ , такой что

$\forall\varphi\in\mathcal{E}:\;\lang\delta;\;\varphi\rang=\varphi(0).$

Непрерывность означает, что если $\varphi_n\to\varphi$ , то $\lang\delta;\;\varphi_n\rang\to\lang\delta;\;\varphi\rang$ . Здесь $\lang\delta;\;\varphi\rang$ — значение функционала на функции $\varphi$ . Для удобства это записывают как

$\lang\delta;\;\varphi\rang=\int_{-\infty}^\infty\delta(x)\varphi(x)\,dx.$

Заметим, что при таком подходе интегральная запись есть не больше, чем формальное обозначение, облегчающее восприятие формул.

Дельта-функция по Коломбо

Используемому для работы с дельта-функцией интегральному выражению можно придать смысл, близкий к интуитивному, в рамках теории алгебры обобщённых функций Коломбо [1].

Пусть $\mathcal{D}$ — множество бесконечно дифференцируемых функций $f\colon\R\to\R$ с компактным носителем, то есть не равных нулю лишь на ограниченном множестве. Рассмотрим множество функций

$\mathcal{A}=\left\{\varphi\in\mathcal{D}\,\bigg|\int_\R\varphi(x)\,dx=1,\;\int_\R x\varphi(x)\,dx=0\right\}.$

Обобщённая функция — это класс эквивалентности функций $R\colon\mathcal{A}\times\R\to\R,$ $R\colon(\varphi,\;x)\mapsto R(\varphi,\;x),$ бесконечно дифференцируемых по x при каждом $\varphi\in\mathcal{A}$ и удовлетворяющих некоторому условию умеренности (полагая $\varphi_\varepsilon(x)=\varepsilon^{-1}\varphi(x\varepsilon^{-1}),$ $R(\varphi_\varepsilon,\;x)$ и все её производные по x достаточно медленно растут при $\varepsilon\to 0$ ). Две функции полагаются эквивалентными, если $R_1-R_2\in\mathcal{N}$ , где $\mathcal{N}$ — ещё один класс функций с ограничениями на рост $R(\varphi_\varepsilon,\;x)$ при $\varepsilon\to 0.$

Дельта-функция определяется как $\delta(\varphi,\;x)=\varphi(-x).$ Преимущество подхода Коломбо в том, что его обобщённые функции образуют коммутативную ассоциативную алгебру, при этом на множество обобщённых функций естественно продолжаются понятия интегрирования, дифференцирования, пределов, даже значения в точке. В этом смысле на дельта-функцию действительно можно смотреть как на функцию, равную 0 везде, кроме точки 0, и равную бесконечности в нуле, так как теория Коломбо включает в себя теорию бесконечно больших и бесконечно малых чисел, аналогично нестандартному анализу.

Подход Егорова

Аналогичная теория обобщённых функций была изложена в работе Ю. В. Егорова[2]. Хотя она не эквивалентна теории Коломбо, конструкция значительно проще и обладает большинством желаемых свойств.

Обобщённая функция — это класс эквивалентности последовательностей $f=(f_1,\;f_2,\;\ldots),\;f_i\in C^\infty(\R).$ Последовательности и $\tilde f$ считаются эквивалентными, если для любого компакта $\Omega\Subset\R$ функции последовательностей совпадают на $\Omega$ начиная с некоторого номера:

$f\sim\tilde f\iff\forall\Omega\Subset\R\ \exists N\ \forall k>N\colon f_k|_\Omega={\tilde f}_k|_\Omega.$

Всевозможные операции над последовательностями (умножение, сложение, интегрирование, дифференцирование, композиция, …) определяются покомпонентно. Например, интеграл по множеству I определяется как класс эквивалентности последовательности

$\int_I f(x)\,dx=[(a_1,\;a_2,\;\ldots)],\;a_i=\int_I f_i(x)\,dx.$

Две обобщённые функции слабо равны, если для любой бесконечно гладкой функции $\varphi$

$\lim_{k\to\infty}\int_I(f_k(x)-{\tilde f}_k(x))\varphi(x)\,dx=0.$

При этом дельта-функция определяется любой дельта-образной последовательностью (см. ниже), все такие обобщённые функции слабо равны.

Свойства

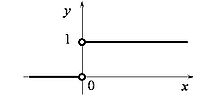
Функция Хевисайда.

Первообразной одномерной дельта-функции является функция Хевисайда:

$\theta(x)=\left\{\begin{array}{*{35}{l}} 0, & x<0, \\ \dfrac{1}{2}, & x=0, \\ 1, & x>0. \\ \end{array}\right.$

Фильтрующее свойство дельта-функции:

$\int\limits_{-\infty}^{+\infty}f(x)\delta(x-x_0)\,dx=f(x_0).$

δ-Функция как слабый предел

Пусть $\int\limits_{-\infty}^{+\infty}f(x)\,dx=1.$

Тогда последовательность

f_n(x)=nf(nx)

слабо сходится к $\delta$ -функции.

Часто в качестве ~f(x) выбирают

$f(x)=\frac{\sin x}{\pi x},$

дающую последовательность

$f_n(x)=n\frac{\sin(nx)}{n\pi x}.$

Если нужно, чтобы члены последовательности были всюду положительными функциями, можно исходить из Гауссова колокола:

$f(x)=\frac1{\sqrt{\pi}}e^{-x^2},$

$f_n(x)=\frac{n}{\sqrt{\pi}}e^{-(nx)^2}.$

Интегральное представление

Во многих приложениях оказывается удобным интегральное представление дельта-функции:

$\delta(t)=\frac{1}{2\pi}\int\limits_{-\infty}^{+\infty}e^{i\omega t}\,d\omega.$

Доказательство

Рассмотрим интеграл

$I(t)=\frac{1}{2\pi}\int\limits_{-\infty}^\infty e^{i\omega t}\,d\omega,$ (1)

который можно интерпретировать как предел

$I(t)=\lim_{N\to\infty}I_N(t),\,$

где

$I_N(t)=\frac{1}{2\pi}\int\limits_{-N}^N e^{i\omega t}\,d\omega=\frac{1}{\pi}N\frac{\sin{tN}}{tN}.$ (2)

Известно, что

$\int\limits_{-\infty}^\infty\frac{\sin t}{t}\,dt=\pi.$ (3)

В силу (3) для любого справедливо равенство:

$\int\limits_{-\infty}^{\infty}I_N(t)\,dt=\frac{1}{\pi}\int\limits_{-\infty}^\infty\frac{\sin{tN}}{tN}\,d(tN)=1.$ (4)

Можно показать (см. выше), что при неограниченном росте N для функции (2) оказываются верными все свойства дельта-функции и она в некотором смысле стремится к $~\delta(t).$

Производная дельта-функции

Фундаментальное выражение, описывающее производную дельта-функции $\delta(x)$ :

$\int\limits_{-\infty}^{+\infty}f(x)\delta^\prime(x-a)\,dx=-f^\prime(a)$

(распространение на случай подынтегральных выражений, содержащих дельта-функцию, интегрирования по частям).

Аналогично для _n_-й производной дельта-функции:

$\int\limits_{-\infty}^{+\infty}f(x)\delta^{[n]}(x-a)\,dx=-\int\limits_{-\infty}^{+\infty}\frac{\partial f}{\partial x}\delta^{[n-1]}(x-a)\,dx.$

А проинтегрировав так по частям n раз, получим в конце концов:

$\int\limits_{-\infty}^{+\infty}f(x)\delta^{[n]}(x-a)\,dx=\left.(-1)^n\frac{\partial^n f(x)}{\partial x^n}\right|_{x=a}.$

Подставив же в первую формулу f(x)=xg(x) и a=0, убедимся, что

$x\delta^\prime(x)=-\delta(x).$

Для производной дельта-функции также верны следующие тождества:

$\delta^\prime(-x)=-\delta^\prime(x);$

$f(x)\delta^\prime(x)=f(0)\delta^\prime(x)-f^\prime(0)\delta(x).$

Преобразование Фурье

В этом параграфе мы будем применять нормировку, соответствующую соглашению о единичном коэффициенте в обратном преобразовании, то есть имея в виду $f(t)=\frac{1}{\sqrt{2\pi}}\int\limits{-\infty}^{+\infty}F(\omega)e^{i\omega t}\,d\omega.$
Формулы этого параграфа имеют соответствующие аналоги для многомерного преобразования Фурье.

К дельта-функции можно применить преобразование Фурье:

$F\left\{\delta(\omega)\right\}=\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty}\delta(t)\cdot e^{-i\omega t}\,dt=\frac{1}{\sqrt{2\pi}}e^{-i\omega\cdot 0}=\frac{1}{\sqrt{2\pi}}.$

В результате получается, что спектр (фурье-образ) $\delta$ -функции является просто константой:

$F\left\{\delta(\omega)\right\}=\frac{1}{\sqrt{2\pi}}.$

То есть, как и было показано выше,

$\delta(t)=\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty}\frac{1}{\sqrt{2\pi}}e^{i\omega t}\,d\omega=\frac{1}{2\pi}\int\limits_{-\infty}^{+\infty}e^{i\omega t}\,d\omega.$

Представление многомерных дельта-функций в различных системах координат

В _n_-мерном пространстве в декартовых координатах (ортонормированном базисе):

$\int\delta^n(x_1,\;x_2,\;\ldots,\;x_n)\,d^n x=1;$

$\delta^n(x_1,\;x_2,\;\ldots,\;x_n)=\delta(x_1)\delta(x_2)\ldots\delta(x_n).$

В двумерном пространстве:

$\iint\limits_{-\infty}^{+\infty}\delta^2(x,\;y)\,dx\,dy=1;$

$\delta^2(ax,\;by)=\frac{1}{\left|ab\right|}\delta^2(x,\;y);$

$\delta^2(x,\;y)=\delta(x)\delta(y).$

В полярных координатах:

$\delta^2(r,\;\varphi)=\frac{\delta(r)}{\pi\left|r\right|}$ — несмещённая относительно начала координат (с особенностью при _r_=0),

$\frac{\delta(r-r_0)\delta(\varphi-\varphi_0)}{|r|}$ — с особенностью в точке общего положения $(r_0,\;\varphi_0);$ при _r_=0 доопределяется нулём.

В трехмёрном пространстве:

$\iiint\limits_{-\infty}^{+\infty}\delta^3(x,\;y,\;z)\,dx\,dy\,dz=1;$

$\delta^3(x,\;y,\;z)=\delta(x)\delta(y)\delta(z).$

В цилиндрической системе координат:

$\delta^3(r,\;\theta,\;z)=\frac{\delta(r)\delta(z)}{\pi r}$ — несмещённая относительно начала координат (с особенностью при $r=0,\;z=0$ ),

$\frac{\delta(r-r_0)\delta(\varphi-\varphi_0)\delta(z-z_0)}{|r|}$ — с особенностью в точке общего положения $(r_0,\;\varphi_0,\;z_0);$ при _r_=0 доопределяется нулём.

В сферической системе координат:

$\delta^3(r,\;\theta,\;\varphi)=\frac{\delta(r)}{4\pi r^2}$ — несмещённая относительно начала координат (с особенностью при _r_=0).

Физическая интерпретация

Вблизи заряжённой точки поле бесконечно, ряды Тейлора для поля не сходятся, поэтому вводят специальные функции. Одной из таких функций является дельта-функция. Вопрос о поле точечной заряженной частицы сравнительно сложен, поэтому рассмотрим сначала более простой пример.

Мгновенное ускорение

Пусть частица, движущаяся вдоль прямой, при ударе пренебрежимо малой длительности скачком приобретают какую-то скорость. Зададимся вопросом: как рассчитать ускорение, приобретенное телом? Построим график зависимости изменения скорости от времени. График будет иметь следующий вид:

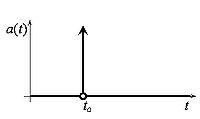
Данный график почти всюду является графиком функции Хевисайда. Производная функции Хевисайда является единичной дельта-функцией, график которой условно можно изобразить как

Данный график отображает бесконечное ускорение при мгновенном наборе скорости. В общем случае ускорение при ударе можно записать как

$a(t)=\nu\delta(t-t_a).\$

Масса материальной точки

Если нужно найти суммарную массу (или заряд) некоторого непрерывного распределения плотности (или плотности заряда) $m=\int\rho_\mathrm{contin},$ содержащего, кроме того, точечные массы (заряды), то удобно вместо формулы, учитывающей отдельно дискретные массы и непрерывную конечную плотность:

$m=\int\rho_\mathrm{contin}(\mathbf{x})\,dV+\sum_i q_i$

записывать просто:

$m=\int\rho(\mathbf{x})\,dV,$

имея в виду, что $\rho(\mathbf{x})$ имеет как непрерывную, так и дельтообразные (по одной для каждой точечной массы) составляющие:

$\rho(\mathbf{x})=\rho_\mathrm{contin}(\mathbf{x})+\sum_i q_i\delta(\mathbf{x}-\mathbf{x}_i).$

Другие примеры

Дельта-функция применяется в математической физике при решении задач, в которые входят сосредоточенные величины. В квазиклассическом пределе ( $\hbar\rightarrow 0$ ) квантовой механики волновые функции локализуются в волновые пакеты с дельтообразными (то есть имеющими в пределе форму дельта-функции) огибающими, и области их локализации движутся по классическим траекториям согласно уравнениям Ньютона.
Преобразование Фурье синуса является дельта-функцией. Это позволяет более удобно и математически строго формулировать различные задачи, связанные с преобразованием Фурье, которые очень многочисленны: волновая оптика, акустика, теория колебаний. В квантовой механике преобразования Фурье волновых функций играют первостепенную принципиальную и техническую роль, именно для неё Дирак впервые ввёл дельта-функцию.
Дельта-функции играют роль собственных функций оператора с непрерывным спектром в представлениях, где этот оператор диагонален. Таким образом, они играют роль базиса в диагональном представлении оператора.
Важным применением дельта-функции является их участие в аппарате функций Грина линейных операторов. Для линейного оператора L, действующего на обобщённые функции над многообразием M, уравнение, определяющее функцию Грина g с источником в точке имеет вид

$L\,g(x,\;x_0)=\delta(x-x_0).$

Особенно часто встречается применение этого аппарата к оператору Лапласа (электростатика, теплопроводность, диффузия, механическая теория упругости) и подобным ему операторам, таким как Оператор Д’Аламбера (акустика, электродинамика, квантовая теория поля, где функция Грина часто носит специальное название пропагатора).

Для лапласиана в $\R^3$ функцией Грина является функция 1/r, так что

$\Delta\left(\frac{1}{r}\right)=-4\pi\delta(r),$

где r — расстояние до начала координат. Этот факт используется для доказательства того, что выражение для скалярного потенциала

$\Phi(\mathbf{x})=-\int\frac{\varrho(\mathbf{x}^\prime)}{\left|\mathbf{x}-\mathbf{x}^\prime\right|}\,d^3x^\prime$

удовлетворяет уравнению Пуассона:

$\Delta\Phi=-4\pi\varrho.$

Примечания

↑ Colombeau J. F. Elementary Introduction to New Generalized Functions. — Amsterdam: Elsevier Science Publishers B. V., 1985. — 281 с. — ISBN 978-0-444-87756-7
↑ Егоров Ю. В. К теории обобщенных функций // УМН. — 1990. — В. 5 (275). — Т. 45. — С. 3—40.

Литература

Дирак П. А. М. Основы квантовой механики / Пер. с англ. — М., 1932 (есть много переизданий).
Кудрявцев Л. Д. Краткий курс математического анализа. — Том 2. — ISBN 5-9221-0185-4.
Weisstein, Eric W. Delta Function (англ.) на сайте Wolfram MathWorld.
Хермандер Л. Анализ линейных дифференциальных уравнений. — Том 1.
Хермандер Л. Линейные дифференциальные операторы в частных производных.
Гельфанд И. М., Шилов Г. Е. Обобщённые функции и действия над ними.
Краснопевцев Е. А. Математические методы физики. Избранные вопросы.