Теорема Ньютона — Лейбница | это... Что такое Теорема Ньютона — Лейбница? (original) (raw)

Теорема Ньютона — Лейбница

Формула Ньютона — Лейбница или теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.

Доказательство

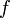Пусть на отрезке $\left [ a,b \right ]$ задана интегрируемая функция $\textstyle f$ . Начнем с того, что отметим, что

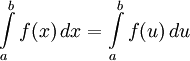
$\int\limits_a^b f(x)\,dx =\int\limits_a^b f(u)\,du$

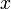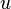то есть не имеет никакого значения, какая буква ( $\textstyle x$ или $\textstyle u$ ) стоит под знаком 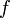$\textstyle f$ в определенном интеграле по отрезку $\left [ a,b \right ]$ .

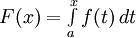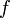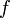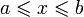Зададим произвольное значение $\textstyle x \in \left [ a,b \right ]$ и определим новую функцию $\textstyle F(x) = \int\limits_a^x f(t) \,dt$ . Она определена для всех значений $\textstyle x \in \left [ a,b \right ]$ , потому что мы знаем, что если существует интеграл от $\textstyle f$ на $\left [ a,b \right ]$ , то существует также интеграл от $\textstyle f$ на $\left [ a,x \right ]$ , где $a \leqslant x \leqslant b$ . Напомним, что мы считаем по определению

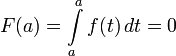$F(a) = \int\limits_a^a f(t)\,dt = 0$ (1)

Заметим, что

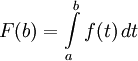
$F(b) = \int\limits_a^b f(t)\,dt$

Покажем, что 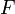$\textstyle F$ непрерывна на отрезке $\left [ a,x \right ]$ . В самом деле, пусть $x, x + h \in \left [ a,x \right ]$ ; тогда

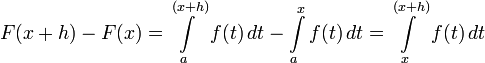
$F(x + h) - F (x) = \int\limits_a^{(x+h)} f(t)\,dt - \int\limits_a^x f(t)\,dt = \int\limits_x^{(x+h)} f(t)\,dt$

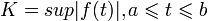и если $K = sup |f(t)|, a \leqslant t \leqslant b$ , то

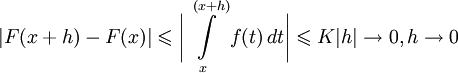
$|F(x + h) - F (x)| \leqslant \bigg| \int\limits_x^{(x+h)} f(t)\,dt \bigg| \leqslant K |h|\to 0 , h\to 0$

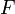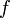Таким образом, $\textstyle F$ непрерывна на $\left [ a,x \right ]$ независимо от того, имеет или не имеет $\textstyle f$ разрывы; важно, что 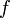$\textstyle f$ интегрируема на $\left [ a,x \right ]$ .

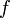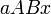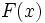На рисунке изображен график $\textstyle f$ . Площадь переменной фигуры $\textstyle aABx$ равна $\textstyle F(x)$ . 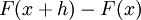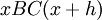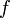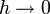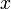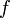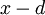Ее приращение $\textstyle F(x + h) - F(x)$ равно площади фигуры $\textstyle xBC(x + h)$ , которая в силу ограниченности $\textstyle f$ , очевидно, стремится к нулю при $h \to 0$ независимо от того, будет ли $\textstyle x$ точкой непрерывности или разрыва $\textstyle f$ , например точкой $\textstyle x - d$ .

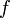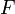Пусть теперь функция $\textstyle f$ не только интегрируема на $\left [ a,x \right ]$ , но непрерывна в точке $x \in \left [ a,x \right ]$ . Докажем, что тогда $\textstyle F$ имеет в этой точке производную, равную

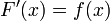$\textstyle F'(x) = f (x)$ (2)

В самом деле, для указанной точки 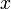$\textstyle x$

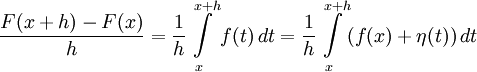
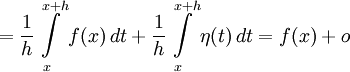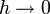$\dfrac{F (x+h) - F (x)}{h} = \dfrac{1}{h} \int\limits_x^{x+h} f(t)\,dt = \dfrac{1}{h} \int\limits_x^{x+h} (f(x) +\eta (t)) \,dt$ $=\dfrac{1}{h} \int\limits_x^{x+h} f(x)\,dt + \dfrac{1}{h} \int\limits_x^{x+h} \eta(t)\,dt = f(x)+ o$ (1) , $h \to 0$ (3)

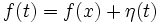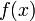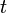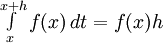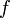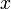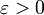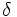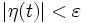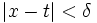Мы положили $\textstyle f(t) = f (x) + \eta(t)$ , а так как $\textstyle f (x)$ постоянная относительно $\textstyle t$ ,TO $\textstyle \int\limits_x^{x+h} f(x) \,dt = f(x)h$ . Далее, в силу непрерывности $\textstyle f$ в точке $\textstyle x$ для всякого $\textstyle \varepsilon > 0$ можно указать такое $\textstyle \delta$ , что $\textstyle |\eta(t)| < \varepsilon$ для $\textstyle |x - t| < \delta$ .

Поэтому

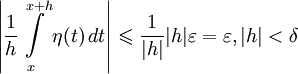
$\left | \dfrac{1}{h} \int\limits_x^{x+h} \eta(t)\,dt \right | \leqslant \dfrac{1}{|h|}|h|\varepsilon = \varepsilon , |h| < \delta$

что доказывает, что левая часть этого неравенства есть о(1) при 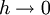$\textstyle h \to 0$ .

Переход к пределу в (3) при 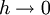$\textstyle h \to 0$ показывает существование производной от 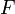$\textstyle F$ в точке 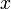$\textstyle x$ и справедливость равенства (2). При 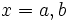$\textstyle x = a,b$ речь здесь идет соответственно о правой и левой производной.

Если функция 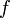$\textstyle f$ непрерывна на $\left [ a,b \right ]$ , то на основании доказанного выше соответствующая ей функция

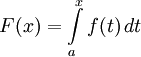$F(x) = \int\limits_a^x f(t)\,dt$ (4)

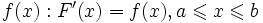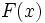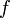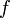имеет производную, равную $\textstyle f(x): F'(x) = f(x) , a \leqslant x \leqslant b$ . Следовательно, функция $\textstyle F(x)$ есть первообразная для $\textstyle f$ на $\left [ a,b \right ]$ .

Мы доказали, что произвольная непрерывная на отрезке $\left [ a,b \right ]$ функция $\textstyle f$ имеет на этом отрезке первообразную, определенную равенством (4). Этим доказано существование первообразной для всякой непрерывной на отрезке функции.

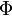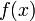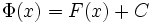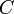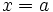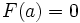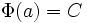Пусть теперь $\textstyle \Phi$ есть произвольная первообразная функции $\textstyle f(x)$ на $\left [ a,b \right ]$ . Мы знаем, что $\textstyle \Phi(x) = F(x) + C$ , где $\textstyle C$ — некоторая постоянная. Полагая в этом равенстве $\textstyle x = a$ и учитывая, что $\textstyle F(a) = 0$ , получим $\textstyle \Phi(a) = C$ .

Таким образом, 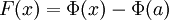$\textstyle F(x) = \Phi(x) - \Phi(a)$ . Но

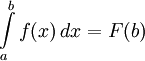
$\int\limits_a^b f(x) \,dx = F(b)$

Поэтому

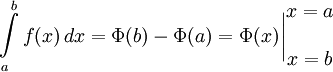
$\int\limits_a^b f(x)\,dx = \Phi(b) - \Phi(a) = \Phi(x) \bigg| \begin{matrix}x = a \\ \\ x = b\end{matrix}$

Вариации и обобщения

Теорема Стокса

Литература

Демидович Б.П. Отдел 3. Формула Ньютона — Лейбница // Сборник задач и упражнений по математическому анализу. — 1990. — (Курс высшей математики и математической физики).

Wikimedia Foundation.2010.