Электромагнитные колебания | это... Что такое Электромагнитные колебания? (original) (raw)

В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники.Эта отметка установлена 15 мая 2011.

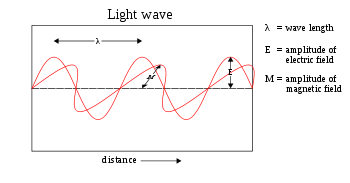
Электромагнитные колебания можно изобразить в виде самораспространяющихся поперечных колебаний электрического и магнитного полей. На рисунке — плоскополяризованная волна, распространяющаяся справа налево. Колебания электрического поля изображены в вертикальной плоскости, а колебания магнитного поля — в горизонтальной.

Электромагнитными колебаниями называются периодические изменения напряженности Е и индукции В.

Электромагнитными колебаниями являются радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое излучение, рентгеновские лучи, гамма-лучи.

Вывод формулы

Электромагнитные волны как универсальное явление были предсказаны классическими законами электричества и магнетизма, известными как уравнения Максвелла. Если вы внимательно посмотрите на уравнение Максвелла в отсутствие источников (зарядов или токов), то обнаружите, что вместе с возможностью, что ничего не случится, теория к тому же допускает нетривиальные решения изменения электрического и магнитного полей. Начнем с уравнений Максвелла для вакуума::

$\nabla \cdot \mathbf{E} = 0 \qquad \qquad \qquad \ \ (1)$

$\nabla \times \mathbf{E} = -\frac{\partial}{\partial t} \mathbf{B} \qquad \qquad (2)$

$\nabla \cdot \mathbf{B} = 0 \qquad \qquad \qquad \ \ (3)$

$\nabla \times \mathbf{B} = \mu_0 \epsilon_0 \frac{\partial}{\partial t} \mathbf{E} \qquad \ \ \ (4)$

где

$\nabla$ — векторный дифференциальный оператор (набла).

Одно из решений,

$\mathbf{E}=\mathbf{B}=\mathbf{0}$ ,

— самое простейшее.

Чтобы найти другое, более интересное решение, мы воспользуемся векторным тождеством, которое справедливо для любого вектора, в виде:

$\nabla \times \left( \nabla \times \mathbf{A} \right) = \nabla \left( \nabla \cdot \mathbf{A} \right) - \nabla^2 \mathbf{A}$

Чтобы посмотреть как мы можем использовать его, возьмем операцию вихря от выражения (2):

$\nabla \times \left(\nabla \times \mathbf{E} \right) = \nabla \times \left(-\frac{\partial \mathbf{B}}{\partial t} \right) \qquad \qquad \qquad \quad \ \ \ (5) \,$

Левая часть эквивалентна:

$\nabla \times \left(\nabla \times \mathbf{E} \right) = \nabla\left(\nabla \cdot \mathbf{E} \right) - \nabla^2 \mathbf{E} = - \nabla^2 \mathbf{E} \qquad \quad \ (6) \,$

где мы упрощаем, используя выше приведенное уравнение (1).

Правая часть эквивалентна:

$\nabla \times \left(-\frac{\partial \mathbf{B}}{\partial t} \right) = -\frac{\partial}{\partial t} \left( \nabla \times \mathbf{B} \right) = -\mu_0 \epsilon_0 \frac{\partial^2}{\partial t^2} \mathbf{E} \qquad (7)$

Уравнения (6) и (7) равны, таким образом эти результаты в векторнозначном дифференциальном уравнении для электрического поля, а именно

$\nabla^2 \mathbf{E} = \mu_0 \epsilon_0 \frac{\partial^2}{\partial t^2} \mathbf{E}$

Применяя аналогичные исходные результаты в аналогичном дифференциальном уравнении для магнитного поля:

$\nabla^2 \mathbf{B} = \mu_0 \epsilon_0 \frac{\partial^2}{\partial t^2} \mathbf{B}$ .

Эти дифференциальные уравнения эквивалентны волновому уравнению:

$\nabla^2 f = \frac{1}{{c_0}^2} \frac{\partial^2 f}{\partial t^2} \,$

где

_c_0 — скорость волны в вакууме;

f — описывает смещение.

Или еще проще:

$\Box^2 f = 0$

где $\Box^2$ — оператор Д’Аламбера:

$\Box^2 = \nabla^2 - \frac{1}{{c_0}^2} \frac{\partial^2}{\partial t^2} = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} - \frac{1}{{c_0}^2} \frac{\partial^2}{\partial t^2} \$

Заметьте, что в случае электрического и магнитного полей скорость:

$c_0 = \frac{1}{\sqrt{\mu_0 \epsilon_0}}$

Которая, как выясняется есть скорость света в вакууме. Уравнения Максвелла объединили диэлектрическую проницаемость вакуума ε0, магнитную проницаемость вакуума μ0 и непосредственно скорость света c0. До этого вывода не было известно, что была такая строгая связь между светом, электричеством и магнетизмом.

Но имеются только два уравнения, а мы начали с четырех, поэтому имеется еще больше информации относительно волн, спрятанных в уравнениях Максвелла. Давайте рассмотрим типичную векторную волну для электрического поля.

$\mathbf{E} = \mathbf{E}_0 f\left( \hat{\mathbf{k}} \cdot \mathbf{x} - c_0 t \right)$

Здесь $\mathbf{E}_0$ — постоянная амплитуда колебаний, — любая мгновенная дифференцируемая функция, $\hat{\mathbf{k}}$ — единичный вектор в направлении распространения, а ${\mathbf{x}}$ i- радиус-вектор. Мы замечаем, что $f\left( \hat{\mathbf{k}} \cdot \mathbf{x} - c_0 t \right)$ — общее решение волнового уравнения. Другими словами

$\nabla^2 f\left( \hat{\mathbf{k}} \cdot \mathbf{x} - c_0 t \right) = \frac{1}{{c_0}^2} \frac{\partial^2}{\partial^2 t} f\left( \hat{\mathbf{k}} \cdot \mathbf{x} - c_0 t \right)$ ,

для типичной волны, распространяющейся в $\hat{\mathbf{k}}$ направлении.

Эта форма будет удовлетворять волновому уравнению, но будет ли она удовлетворять всем уравнениям Максвелла, и с чем соответствуется магнитное поле?

$\nabla \cdot \mathbf{E} = \hat{\mathbf{k}} \cdot \mathbf{E}_0 f'\left( \hat{\mathbf{k}} \cdot \mathbf{x} - c_0 t \right) = 0$

$\mathbf{E} \cdot \hat{\mathbf{k}} = 0$

Первое уравнение Максвелла подразумевает, что электрическое поле ортогонально (перпендикулярно) направлению распространению волны.

$\nabla \times \mathbf{E} = \hat{\mathbf{k}} \times \mathbf{E}_0 f'\left( \hat{\mathbf{k}} \cdot \mathbf{x} - c_0 t \right) = -\frac{\partial}{\partial t} \mathbf{B}$

$\mathbf{B} = \frac{1}{c_0} \hat{\mathbf{k}} \times \mathbf{E}$

Второе уравнение Максвелла порождает магнитное поле. Оставшиеся уравнения будут удовлетворяться выбором $\mathbf{E},\mathbf{B}$ .

Мало того, что волны электрического и магнитного полей распространяются со скоростью света, но они имеют ограниченную ориентацию и пропорциональную величину, E_0 = c_0 B_0 , которую можно сразу же заметить из вектора Пойнтинга. Электрическое поле, магнитное поле и направление распространения волны все являются ортогональными, и распространение волны в том же направлении как вектор $\mathbf{E} \times \mathbf{B}$ .

С точки зрения электромагнитной волны, перемещающейся прямолинейно, электрическое поле может колебаться вверх и вниз, в то время как магнитное поле может колебаться вправо и влево, но эта картина может чередоваться с электрическим полем, колеблющемся вправо и влево, и магнитным полем, колеблющимся вверх и вниз. Эта произвольность в ориентации с предпочтением к направлению распространения известно как поляризация.

Электромагнитные колебания | это... Что такое Электромагнитные колебания? (original) (raw)

Вывод формулы

См. также