Движение Рейдемейстера | это... Что такое Движение Рейдемейстера? (original) (raw)
В математической теории узлов, движением (преобразованием) Рейдемейстера называют одно из трёх локальных движений на диаграмме зацепления. В 1927 Джеймс Александер и Бриггс, а также независимо от них Курт Рейдемейстер, показали, что две диаграммы, относящиеся к одному и тому же узлу, с точностью до плоской изотопии могут быть преобразованы одна в другую с помощью последовательного применения одного из трёх движений Рейдемейстера.
Движения Рейдемейстера
 |
 |
|---|---|
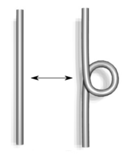
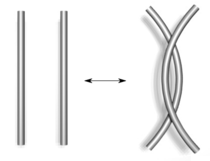
| Тип I | Тип II |
 |
|
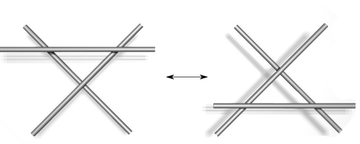
| Тип III |
Каждое движение действует в небольшой области диаграммы и бывает одного из трёх типов:
Тип I. Скручивание и раскручивание в любом направлении.
Тип II. Перемещение одной петли целиком через другую.
Тип III. Перемещение нити целиком над или под пересечением.
Заметим, что другие части диаграммы не отображены на схеме движения, а также, что плоская изотопия может исказить рисунок. Нумерация типов движений соответствует числу нитей, вовлечённых в него, к примеру, движение типа II действует на двух нитях диаграммы.
Один из важных случаев, когда требуются движения Рейдемейстера — это определения инвариантов узлов. Инвариант определяют, как свойство диаграммы узла, которое не меняется при любых движениях Рейдемейстера. Множество важных инвариантов можно определить таким образом, включая полином Джонса.
Только движения типа I изменяют число закрученности зацепления. Движение типа III — единственное, которое не изменяет число пересечений на диаграмме.
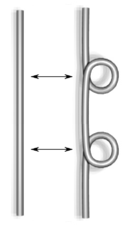
В приложениях, таких как исчисление Кирби, в котором искомый класс эквивалентности диаграмм узла является не узлом, а оснащённым узлом, необходимо заменить движение типа I движением «модифицированного типа I» (тип I'), состоящем из двух движений типа I в противоположных направлениях. Движение типа I' не затрагивает ни оснащённость зацепления, ни полный индекс извивания диаграммы узла.
Модифицированное движение Рейдемейстера
 |
|---|
| Тип I' |
Брюс Трэйс показал, что две диаграммы связаны только движениями типов II и III тогда и только тогда, когда у них одинаковые числа закрученности и вращения(en:winding number). Кроме того, совместная работа О. Остлунд, В. О. Мантурова и Т.Хаге показывает, что для каждого узла есть такая пара диаграмм, что любая последовательность движений Рейдемейстера, переводящая одну диаграмму в другую, должна состоять из движений всех трёх типов. Александр Ковард показал, что для диаграмм зацеплений, представляющих эквивалентные зацепления, есть последовательность движений, упорядоченная по типам: сначала выполняются движения типа I, затем — типа II, типа III и снова типа II. Движения до движений типа III увеличивают число пересечений, а после них — уменьшают.
В другом русле, Стефан Галатоло, и независимо Джоэл Хас и Джеффри Лагарьяс (с лучшим ограничением), показали, что существует верхняя граница (зависящая от числа пересечений) количества движений Рейдемейстера необходимая, чтобы превратить диаграмму тривиального узла в его стандартную диаграмму. Это предоставляет малопродуктивный алгоритм для решения задачи развязывания.
Чюичиро Хаяши доказал, что есть также верхняя граница, зависящая от числа пересечений, движений Рейдемейстера, необходимых для расщепления зацепления
Литература
- J. W. Alexander; G. B. Briggs, On types of knotted curves. Ann. of Math. (2) 28 (1926/27), no. 1-4, 562—586.
- Kurt Reidemeister, Elementare Begru"ndung der Knotentheorie, Abh. Math. Sem. Univ. Hamburg 5 (1926), 24-32
- Bruce Trace, On the Reidemeister moves of a classical knot. Proc. Amer. Math. Soc. 89 (1983), no. 4, 722—724.
- Tobias Hagge, Every Reidemeister move is needed for each knot type. Proc. Amer. Math. Soc. 134 (2006), no. 1, 295—301.
- Stefano Galatolo, On a problem in effective knot theory. Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (9) Mat. Appl. 9 (1998), no. 4, 299—306 (1999).
- Joel Hass; Jeffrey Lagarias, The number of Reidemeister moves needed for unknotting. J. Amer. Math. Soc. 14 (2001), no. 2, 399—428
- Chuichiro Hayashi, The number of Reidemeister moves for splitting a link. Math. Ann. 332 (2005), no. 2, 239—252.