Локальная теорема Муавра — Лапласа | это... Что такое Локальная теорема Муавра — Лапласа? (original) (raw)

Локальная теорема Муавра — Лапласа

Локальная теорема Муавра — Лапласа

ЛАПЛАСА ТЕОРЕМА - одна из предельных теорем теории вероятностей. Если при каждом из n независимых испытаний вероятность появления некоторого случайного события Е равна р (0"р"1) и m - число испытаний, в которых Е фактически наступает, то вероятность неравенства близка (при больших n) к значению интеграла Лапласа. Установлена П. Лапласом (1812).

Применение

Используется в теории вероятностей.

При рассмотрении количества m появлений события A в n испытаниях Бернулли чаще всего нужно найти вероятность того, что m заключено между некоторыми значениями a и b. Так как при достаточно больших n промежуток [a,_b_] содержит большое число единиц, то непосредственное использование биномиального распределения

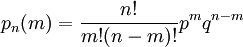
$p_n(m)=\frac{n!}{m!(n - m)!}p^mq^{n-m}$

требует громоздких вычислений, так как нужно суммировать большое число определённых по этой формуле вероятностей.

Поэтому используют асимптотическое выражение для биномиального распределения при условии, что p фиксированно, а 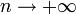$n\rightarrow+\infty$ . Теорема Муавра-Лапласа утверждает, что таким асимптотическим выражением для биномиального распределения является нормальная функция.

Формулировка

Если в схеме Бернулли n стремится к бесконечности, p (0 < p < 1) постоянно, величина 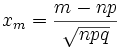$x_m = \frac{m - np}{\sqrt{npq}}$ ограничена равномерно по m и n 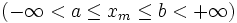$(-\infty < a \le x_m \le b < +\infty)$ , то

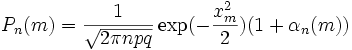
$P_n(m) = \frac{1}{\sqrt{2\pi npq}}\exp(-\frac{x_m^2}{2})(1 + \alpha_n(m))$

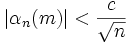где $\left| \alpha_n(m) \right| < \frac{c}{\sqrt{n}}$ , c > 0, c - постоянная.

Приближённую формулу

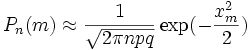
$P_n(m) \approx \frac{1}{\sqrt{2\pi npq}}\exp(-\frac{x_m^2}{2})$

рекомендуется применять при n > 100 и npq > 20.

Доказательство

Для доказательства Теоремы будем использовать формулу Стирлинга из математического анализа:

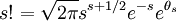$s!=\sqrt{2\pi}s^{s+1/2}e^{-s}e^{\theta_s}$ (1)

где 0 < θ_s_ < 1 / 12_s_. При больших s величина θ очень мала, и приближённая формула Стирлинга, записанная в простом виде,

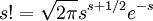$s!=\sqrt{2\pi}s^{s+1/2}e^{-s}$ (2)

даёт малую относительную ошибку, быстро стремящуюся к нулю, когда 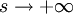$s\rightarrow+\infty$ .

Нас будут интересовать значения m, не очень отличающиеся от наивероятнейшего. Тогда при фиксированном p условие 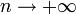$n\rightarrow+\infty$ будет так же означать, что

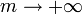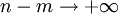$m\rightarrow+\infty$ , $n-m\rightarrow+\infty$ (3)

Поэтому использование приближённой формулы Стирлинга для замены факториалов в биномиальном распределении допустимо, и мы получаем

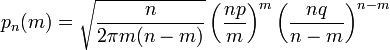$p_n(m)=\sqrt{\frac{n}{2\pi m(n-m)}}\left(\frac{np}{m}\right)^{m}\left(\frac{nq}{n-m}\right)^{n-m}$ (4)

Также понадобится использование отклонения относительной частоты от наивероятнейшего значения

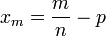$x_m=\frac{m}{n}-p$ (5)

Переписываем полученное ранее биномиальное распределение с факториалами, заменёнными по приближённой формуле Стирлинга:

$p_n(m)=\left[2\pi n(p+x_m)(q-x_m)\right]^{-1/2}\left(1+\frac{x_m}{p}\right)^{-n(p+x_m)}\left(1-\frac{x_m}{q}\right)^{-n(q-x_m)}$ (6)

Предположим, что

x m < p q (7)

Взяв логарифм второго и третьего множителей равенства (6), применим разложение в ряд Тейлора:

$-n\left[(p+x_m)\ln{\left(1+\frac{x_m}{p}\right)} + (q-x_m)\ln{\left(1-\frac{x_m}{q}\right)}\right]=$

$-n\left[(p+x_m)\left(\frac{x_m}{p}-\frac{x_m^2}{2p^2}+\frac{x_m^3}{3p^3}-\cdots\right)+(q-x_m)\left(-\frac{x_m}{q}-\frac{x_m^2}{2q^2}-\frac{x_m^3}{3q^3}-\cdots\right)\right]$ (8)

Располагаем члены этого разложения по степеням x m:

$-n\left[\frac{x_m^2}{2}\left(\frac{1}{p}+\frac{1}{q}\right)-\frac{x_m^3}{6}\left(\frac{1}{p^2}-\frac{1}{q^2}\right)+\cdots\right]$ (9)

Предположим, что при 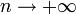$n\rightarrow+\infty$

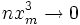$nx_m^3\rightarrow0$ (10)

Это условие, как уже было указанно выше, означает, что рассматриваются значения m, не очень далёкие от наивероятнейшего. Очевидно, что (10) обеспечивает выполнение (7) и (3).

Теперь, пренебрегая вторым и последующими членами в разложении (6), получаем, что логарифм произведения второго и третьего членов произведения в правой части (8) равен

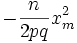$-\frac{n}{2pq}x_m^2$ (11)

Отбрасывая малые слагаемые в скобках первого множителя (6), получаем:

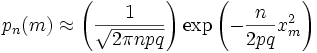$p_n(m)\approx\left(\frac{1}{\sqrt{2\pi npq}}\right)\exp{\left(-\frac{n}{2pq}x_m^2\right)}$ (12)

Обозначив

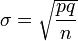$\sigma=\sqrt{\frac{pq}{n}}$ (13)

Переписываем (12) в виде:

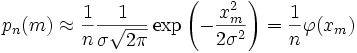$p_n(m)\approx\frac{1}{n}\frac{1}{\sigma\sqrt{2\pi}}\exp{\left(-\frac{x_m^2}{2\sigma^2}\right)}=\frac{1}{n}\varphi(x_m)$ (14)

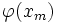Где $\varphi(x_m)$ — нормальная функция.

Поскольку в интервале [m,m + 1) имеется только одно целое число m, то можно сказать, что p n(m) есть вероятность попадания m в интервал [m,m + 1). Из (5) следует, что изменению m на 1 соответствует изменение x m на

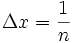$\Delta x=\frac{1}{n}$ (15)

Поэтому вероятность попадания m в интервал [m,m + 1) равна вероятности попадания x m в промежуток [x m,x m + Δ_x_)

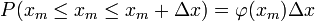$P(x_m \le x_m \le x_m + \Delta x) = \varphi(x_m)\Delta x$ (16)

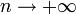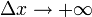Когда $n\rightarrow+\infty$ , $\Delta x\rightarrow+\infty$ и равенство (16) показывает, что нормальная функция 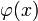$\varphi(x)$ является плотностью случайной переменной x m

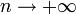
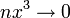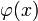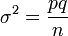Таким образом, если $n\rightarrow+\infty$ $nx^3\rightarrow0$ то для отклонения относительной частоты от наивероятнейшего значения справедлива ассимптотическая формула (16), в которой $\varphi(x)$ — нормальная функция с x m = 0 и $\sigma^2=\frac{pq}{n}$ .

Таким образом теорема доказана.

Литература

Гмурман В.Е. Теория вероятностей и математическая статистика, — М.: Высшее образование. 2005
Ширяев А. Н. Вероятность, — М.: Наука. 1989.
Чистяков В. П. Курс теории вероятностей, — М., 1982.

Wikimedia Foundation.2010.